Problem

You want to preprocess data for use in a neural network.

Solution

Standardize each feature using scikit-learn’s StandardScaler:

# Load libraries
from sklearn import preprocessing
import numpy as np

# Create feature
features = np.array([[-100.1, 3240.1],
                     [-200.2, -234.1],
                     [5000.5, 150.1],
                     [6000.6, -125.1],
                     [9000.9, -673.1]])

# Create scaler
scaler = preprocessing.StandardScaler()

# Transform the feature
features_standardized = scaler.fit_transform(features)

# Show feature
features_standardized

array([[-1.12541308,  1.96429418],
       [-1.15329466, -0.50068741],
       [ 0.29529406, -0.22809346],
       [ 0.57385917, -0.42335076],
       [ 1.40955451, -0.81216255]])

Discussion

While this recipe is very similar to Recipe 4.3, it is worth repeating because of how important it is for neural networks. Typically, a neural network’s parameters are initialized (i.e., created) as small random numbers. Neural networks often behave poorly when the feature values are much larger than parameter values. Furthermore, since an observation’s feature values are combined as they pass through individual units, it is important that all features have the same scale.

For these reasons, it is best practice (although not always necessary; for example, when we have all binary features) to standardize each feature such that the feature’s values have the mean of 0 and the standard deviation of 1. This can be easily accomplished with scikit-learn’s StandardScaler.

You can see the effect of the standardization by checking the mean and standard deviation of our first features:

# Print mean and standard deviation
print("Mean:", round(features_standardized[:,0].mean()))
print('"Standard deviation:", features_standardized[:,0].std())

Mean: 0.0
Standard deviation: 1.0

Problem

You want to design a neural network.

Solution

Use Keras’ Sequential model:

# Load libraries
from keras import models
from keras import layers

# Start neural network
network = models.Sequential()

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=16, activation="relu", input_shape=(10,)))

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=16, activation="relu"))

# Add fully connected layer with a sigmoid activation function
network.add(layers.Dense(units=1, activation="sigmoid"))

# Compile neural network
network.compile(loss="binary_crossentropy", # Cross-entropy
                optimizer="rmsprop", # Root Mean Square Propagation
                metrics=["accuracy"]) # Accuracy performance metric

Using TensorFlow backend.

Discussion

Neural networks consist of layers of units. However, there is incredible variety in the types of layers and how they are combined to form the network’s architecture. At present, while there are commonly used architecture patterns (which we will cover in this chapter), the truth is that selecting the right architecture is mostly an art and the topic of much research.

To construct a feedforward neural network in Keras, we need to make a number of choices about both the network architecture and training process. Remember that each unit in the hidden layers:

1. Receives a number of inputs.

2. Weights each input by a parameter value.

3. Sums together all weighted inputs along with some bias (typically 1).

4. Most often then applies some function (called an activation function).

5. Sends the output on to units in the next layer.

First, for each layer in the hidden and output layers we must define the number of units to include in the layer and the activation function. Overall, the more units we have in a layer, the more our network is able to learn complex patterns. However, more units might make our network overfit the training data in a way detrimental to the performance on the test data.

For hidden layers, a popular activation function is the rectified linear unit (ReLU):

where z is the sum of the weighted inputs and bias. As we can see, if z is greater than 0, the activation function returns z; otherwise, the function returns 0. This simple activation function has a number of desirable properties (a discussion of which is beyond the scope of this book) and this has made it a popular choice in neural networks. We should be aware, however, that many dozens of activation functions exist.

Second, we need to define the number of hidden layers to use in the network. More layers allow the network to learn more complex relationships, but with a computational cost.

Third, we have to define the structure of the activation function (if any) of the output layer. The nature of the output function is often determined by the goal of the network. Here are some common output layer patterns:

Binary classification

One unit with a sigmoid activation function.

Multiclass classification

k units (where k is the number of target classes) and a softmax activation function.

Regression

One unit with no activation function.

Fourth, we need to define a loss function (the function that measures how well a predicted value matches the true value); this is again often determined by the problem type:

Binary classification

Binary cross-entropy.

Multiclass classification

Categorical cross-entropy.

Regression

Mean square error.

Fifth, we have to define an optimizer, which intuitively can be thought of as our strategy “walking around” the loss function to find the parameter values that produce the lowest error. Common choices for optimizers are stochastic gradient descent, stochastic gradient descent with momentum, root mean square propagation, and adaptive moment estimation (more information on these optimizers in “See Also”).

Sixth, we can select one or more metrics to use to evaluate the performance, such as accuracy.

Keras offers two ways for creating neural networks. Keras’ sequential model creates neural networks by stacking together layers. An alternative method for creating neural networks is called the functional API, but that is more for researchers rather than practitioners.

In our solution, we created a two-layer neural network (when counting layers we don’t include the input layer because it does not have any parameters to learn) using Keras’ sequential model. Each layer is “dense” (also called fully connected), meaning that all the units in the previous layer are connected to all the neurals in the next layer. In the first hidden layer we set units=16, meaning that layer contains 16 units with ReLU activation functions: activation='relu'. In Keras, the first hidden layer of any network has to include an input_shape parameter, which is the shape of feature data. For example, (10,) tells the first layer to expect each observation to have 10 feature values. Our second layer is the same as the first, without the need for the input_shape parameter. This network is designed for binary classification so the output layer contains only one unit with a sigmoid activation function, which constrains the output to between 0 and 1 (representing the probability an observation is class 1).

Finally, before we can train our model, we need to tell Keras how we want our network to learn. We do this using the compile method, with our optimization algorithm (RMSProp), loss function (binary_crossentropy), and one or more performance metrics.

See Also

• Losses, Keras

• Loss functions for classification, Wikipedia

• On Loss Functions for Deep Neural Networks in Classification, Katarzyna Janocha, Wojciech Marian Czarnecki

Problem

You want to train a binary classifier neural network.

Solution

Use Keras to construct a feedforward neural network and train it using the fit method:

# Load libraries
import numpy as np
from keras.datasets import imdb
from keras.preprocessing.text import Tokenizer
from keras import models
from keras import layers

# Set random seed
np.random.seed(0)

# Set the number of features we want
number_of_features = 1000

# Load data and target vector from movie review data
(data_train, target_train), (data_test, target_test) = imdb.load_data(
    num_words=number_of_features)

# Convert movie review data to one-hot encoded feature matrix
tokenizer = Tokenizer(num_words=number_of_features)
features_train = tokenizer.sequences_to_matrix(data_train, mode="binary")
features_test = tokenizer.sequences_to_matrix(data_test, mode="binary")

# Start neural network
network = models.Sequential()

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=16, activation="relu", input_shape=(
    number_of_features,)))

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=16, activation="relu"))

# Add fully connected layer with a sigmoid activation function
network.add(layers.Dense(units=1, activation="sigmoid"))

# Compile neural network
network.compile(loss="binary_crossentropy", # Cross-entropy
                optimizer="rmsprop", # Root Mean Square Propagation
                metrics=["accuracy"]) # Accuracy performance metric

# Train neural network
history = network.fit(features_train, # Features
                      target_train, # Target vector
                      epochs=3, # Number of epochs
                      verbose=1, # Print description after each epoch
                      batch_size=100, # Number of observations per batch
                      validation_data=(features_test, target_test)) # Test data

Using TensorFlow backend.


Train on 25000 samples, validate on 25000 samples
Epoch 1/3
25000/25000 [==============================]
- 1s - loss: 0.4215 - acc: 0.8105 - val_loss: 0.3386 - val_acc: 0.8555
Epoch 2/3
25000/25000 [==============================]
- 1s - loss: 0.3242 - acc: 0.8645 - val_loss: 0.3258 - val_acc: 0.8633
Epoch 3/3
25000/25000 [==============================]
- 1s - loss: 0.3121 - acc: 0.8699 - val_loss: 0.3265 - val_acc: 0.8599

Discussion

In Recipe 20.2, we discussed how to construct a neural network using Keras’ sequential model. In this recipe we train that neural network using real data. Specifically, we use 50,000 movie reviews (25,000 as training data, 25,000 held out for testing), categorized as positive or negative. We convert the text of the reviews into 5,000 binary features indicating the presence of one of the 1,000 most frequent words. Put more simply, our neural networks will use 25,000 observations, each with 1,000 features, to predict if a movie review is positive or negative.

The neural network we are using is the same as the one in Recipe 20.2 (see there for a detailed explanation). The only addition is that in that recipe we only created the neural network, we didn’t train it.

In Keras, we train our neural network using the fit method. There are six significant parameters to define. The first two parameters are the features and target vector of the training data. We can view the shape of feature matrix using shape:

# View shape of feature matrix
features_train.shape

(25000, 1000)

The epochs parameter defines how many epochs to use when training the data. verbose determines how much information is outputted during the training process, with 0 being no output, 1 outputting a progress bar, and 2 one log line per epoch. batch_size sets the number of observations to propagate through the network before updating the parameters.

Finally, we held out a test set of data to use to evaluate the model. These test features and test target vector can be arguments of validation_data, which will use them for evaluation. Alternatively, we could have used validation_split to define what fraction of the training data we want to hold out for evaluation.

In scikit-learn the fit method returned a trained model, but in Keras the fit method returns a History object containing the loss values and performance metrics at each epoch.

Problem

You want to train a multiclass classifier neural network.

Solution

Use Keras to construct a feedforward neural network with an output layer with softmax activation functions:

# Load libraries
import numpy as np
from keras.datasets import reuters
from keras.utils.np_utils import to_categorical
from keras.preprocessing.text import Tokenizer
from keras import models
from keras import layers

# Set random seed
np.random.seed(0)

# Set the number of features we want
number_of_features = 5000

# Load feature and target data
data = reuters.load_data(num_words=number_of_features)
(data_train, target_vector_train), (data_test, target_vector_test) = data

# Convert feature data to a one-hot encoded feature matrix
tokenizer = Tokenizer(num_words=number_of_features)
features_train = tokenizer.sequences_to_matrix(data_train, mode="binary")
features_test = tokenizer.sequences_to_matrix(data_test, mode="binary")

# One-hot encode target vector to create a target matrix
target_train = to_categorical(target_vector_train)
target_test = to_categorical(target_vector_test)

# Start neural network
network = models.Sequential()

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=100,
                         activation="relu",
                         input_shape=(number_of_features,)))

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=100, activation="relu"))

# Add fully connected layer with a softmax activation function
network.add(layers.Dense(units=46, activation="softmax"))

# Compile neural network
network.compile(loss="categorical_crossentropy", # Cross-entropy
                optimizer="rmsprop", # Root Mean Square Propagation
                metrics=["accuracy"]) # Accuracy performance metric

# Train neural network
history = network.fit(features_train, # Features
                      target_train, # Target
                      epochs=3, # Three epochs
                      verbose=0, # No output
                      batch_size=100, # Number of observations per batch
                      validation_data=(features_test, target_test)) # Test data

Using TensorFlow backend.

Discussion

In this solution we created a similar neural network to the binary classifier from the last recipe, but with some notable changes. First, our data is 11,228 Reuters newswires. Each newswire is categorized into 46 topics. We prepared our feature data by converting the newswires into 5,000 binary features (denoting the presence of a certain word in the newswires). We prepared the target data by one-hot encoding it so that we obtain a target matrix denoting which of the 46 classes an observation belongs to:

# View target matrix
target_train

array([[ 0.,  0.,  0., ...,  0.,  0.,  0.],
       [ 0.,  0.,  0., ...,  0.,  0.,  0.],
       [ 0.,  0.,  0., ...,  0.,  0.,  0.],
       ...,
       [ 0.,  0.,  0., ...,  0.,  0.,  0.],
       [ 0.,  0.,  0., ...,  0.,  0.,  0.],
       [ 0.,  0.,  0., ...,  0.,  0.,  0.]])

Second, we increased the number of units in each of the hidden layers to help the neural network represent the more complex relationship between the 46 classes.

Third, since this is a multiclass classification problem, we used an output layer with 46 units (one per class) containing a softmax activation function. The softmax activation function will return an array of 46 values summing to 1. These 46 values represent an observation’s probability of being a member of each of the 46 classes.

Fourth, we used a loss function suited to multiclass classification, the categorical cross-entropy loss function, categorical_crossentropy.

Problem

You want to train a neural network for regression.

Solution

Use Keras to construct a feedforward neural network with a single output unit and no activation function:

# Load libraries
import numpy as np
from keras.preprocessing.text import Tokenizer
from keras import models
from keras import layers
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn import preprocessing

# Set random seed
np.random.seed(0)

# Generate features matrix and target vector
features, target = make_regression(n_samples = 10000,
                                   n_features = 3,
                                   n_informative = 3,
                                   n_targets = 1,
                                   noise = 0.0,
                                   random_state = 0)

# Divide our data into training and test sets
features_train, features_test, target_train, target_test = train_test_split(
features, target, test_size=0.33, random_state=0)

# Start neural network
network = models.Sequential()

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=32,
                         activation="relu",
                         input_shape=(features_train.shape[1],)))

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=32, activation="relu"))

# Add fully connected layer with no activation function
network.add(layers.Dense(units=1))

# Compile neural network
network.compile(loss="mse", # Mean squared error
                optimizer="RMSprop", # Optimization algorithm
                metrics=["mse"]) # Mean squared error

# Train neural network
history = network.fit(features_train, # Features
                      target_train, # Target vector
                      epochs=10, # Number of epochs
                      verbose=0, # No output
                      batch_size=100, # Number of observations per batch
                      validation_data=(features_test, target_test)) # Test data

Using TensorFlow backend.

Discussion

It is completely possible to create a neural network to predict continuous values instead of class probabilities. In the case of our binary classifier (Recipe 20.3) we used an output layer with a single unit and a sigmoid activation function to produce a probability that an observation was class 1. Importantly, the sigmoid activation function constrained the outputted value to between 0 and 1. If we remove that constraint by having no activation function, we allow the output to be a continuous value.

Furthermore, because we are training a regression, we should use an appropriate loss function and evaluation metric, in our case the mean square error:

where n is the number of observations; y_i is the true value of the target we are trying to predict, y, for observation i; and ŷ_i is the model’s predicted value for y_i.

Finally, because we are using simulated data using scikit-learn, make_regression, we didn’t have to standardize the features. It should be noted, however, that in almost all real-world cases standardization would be necessary.

Problem

You want to use a neural network to make predictions.

Solution

Use Keras to construct a feedforward neural network, then make predictions using predict:

# Load libraries
import numpy as np
from keras.datasets import imdb
from keras.preprocessing.text import Tokenizer
from keras import models
from keras import layers

# Set random seed
np.random.seed(0)

# Set the number of features we want
number_of_features = 10000

# Load data and target vector from IMDB movie data
(data_train, target_train), (data_test, target_test) = imdb.load_data(
    num_words=number_of_features)

# Convert IMDB data to a one-hot encoded feature matrix
tokenizer = Tokenizer(num_words=number_of_features)
features_train = tokenizer.sequences_to_matrix(data_train, mode="binary")
features_test = tokenizer.sequences_to_matrix(data_test, mode="binary")

# Start neural network
network = models.Sequential()

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=16,
                         activation="relu",
                         input_shape=(number_of_features,)))

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=16, activation="relu"))

# Add fully connected layer with a sigmoid activation function
network.add(layers.Dense(units=1, activation="sigmoid"))

# Compile neural network
network.compile(loss="binary_crossentropy", # Cross-entropy
                optimizer="rmsprop", # Root Mean Square Propagation
                metrics=["accuracy"]) # Accuracy performance metric

# Train neural network
history = network.fit(features_train, # Features
                      target_train, # Target vector
                      epochs=3, # Number of epochs
                      verbose=0, # No output
                      batch_size=100, # Number of observations per batch
                      validation_data=(features_test, target_test)) # Test data

# Predict classes of test set
predicted_target = network.predict(features_test)

Using TensorFlow backend.

Discussion

Making predictions is easy in Keras. Once we have trained our neural network we can use the predict method, which takes as an argument a set of features and returns the predicted output for each observation. In our solution our neural network is set up for binary classification so the predicted output is the probability of being class 1. Observations with predicted values very close to 1 are highly likely to be class 1, while observations with predicted values very close to 0 are highly likely to be class 0. For example, this is the predicted probability that the first observation in our test feature matrix is class 1:

# View the probability the first observation is class 1
predicted_target[0]

array([ 0.83937484], dtype=float32)

Problem

You want to find the “sweet spot” in a neural network’s loss and/or accuracy score.

Solution

Use Matplotlib to visualize the loss of the test and training set over each epoch:

# Load libraries
import numpy as np
from keras.datasets import imdb
from keras.preprocessing.text import Tokenizer
from keras import models
from keras import layers
import matplotlib.pyplot as plt

# Set random seed
np.random.seed(0)

# Set the number of features we want
number_of_features = 10000

# Load data and target vector from movie review data
(data_train, target_train), (data_test, target_test) = imdb.load_data(
    num_words=number_of_features)

# Convert movie review data to a one-hot encoded feature matrix
tokenizer = Tokenizer(num_words=number_of_features)
features_train = tokenizer.sequences_to_matrix(data_train, mode="binary")
features_test = tokenizer.sequences_to_matrix(data_test, mode="binary")

# Start neural network
network = models.Sequential()

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=16,
                         activation="relu",
                         input_shape=(number_of_features,)))

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=16, activation="relu"))

# Add fully connected layer with a sigmoid activation function
network.add(layers.Dense(units=1, activation="sigmoid"))

# Compile neural network
network.compile(loss="binary_crossentropy", # Cross-entropy
                optimizer="rmsprop", # Root Mean Square Propagation
                metrics=["accuracy"]) # Accuracy performance metric

# Train neural network
history = network.fit(features_train, # Features
                      target_train, # Target
                      epochs=15, # Number of epochs
                      verbose=0, # No output
                      batch_size=1000, # Number of observations per batch
                      validation_data=(features_test, target_test)) # Test data

# Get training and test loss histories
training_loss = history.history["loss"]
test_loss = history.history["val_loss"]

# Create count of the number of epochs
epoch_count = range(1, len(training_loss) + 1)

# Visualize loss history
plt.plot(epoch_count, training_loss, "r--")
plt.plot(epoch_count, test_loss, "b-")
plt.legend(["Training Loss", "Test Loss"])
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.show();

Using TensorFlow backend.

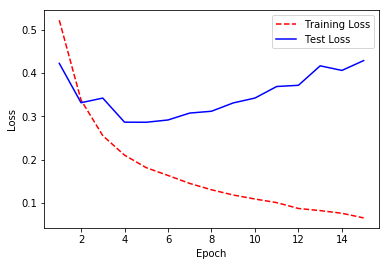
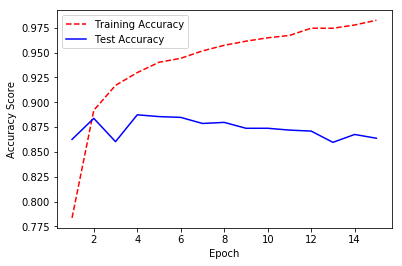
Alternatively, we can use the same approach to visualize the training and test accuracy over each epoch:

# Get training and test accuracy histories
training_accuracy = history.history["acc"]
test_accuracy = history.history["val_acc"]
plt.plot(epoch_count, training_accuracy, "r--")
plt.plot(epoch_count, test_accuracy, "b-")

# Visualize accuracy history
plt.legend(["Training Accuracy", "Test Accuracy"])
plt.xlabel("Epoch")
plt.ylabel("Accuracy Score")
plt.show();

Discussion

When our neural network is new, it will have a poor performance. As the neural network learns on the training data, the model’s error on both the training and test set will tend to increase. However, at a certain point the neural network starts “memorizing” the training data, and overfits. When this starts happening, the training error will decrease while the test error will start increasing. Therefore, in many cases there is a “sweet spot” where the test error (which is the error we mainly care about) is at its lowest point. This effect can be plainly seen in the solution where we visualize the training and test loss at each epoch. Note that the test error is lowest around epoch five, after which the training loss continues to increase while the test loss starts increasing. At this point onward, the model is overfitting.

Problem

You want to reduce overfitting.

Solution

Try penalizing the parameters of the network, also called weight regularization:

# Load libraries
import numpy as np
from keras.datasets import imdb
from keras.preprocessing.text import Tokenizer
from keras import models
from keras import layers
from keras import regularizers

# Set random seed
np.random.seed(0)

# Set the number of features we want
number_of_features = 1000

# Load data and target vector from movie review data
(data_train, target_train), (data_test, target_test) = imdb.load_data(
    num_words=number_of_features)

# Convert movie review data to a one-hot encoded feature matrix
tokenizer = Tokenizer(num_words=number_of_features)
features_train = tokenizer.sequences_to_matrix(data_train, mode="binary")
features_test = tokenizer.sequences_to_matrix(data_test, mode="binary")

# Start neural network
network = models.Sequential()

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=16,
                         activation="relu",
                         kernel_regularizer=regularizers.l2(0.01),
                         input_shape=(number_of_features,)))

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=16,
                         kernel_regularizer=regularizers.l2(0.01),
                         activation="relu"))

# Add fully connected layer with a sigmoid activation function
network.add(layers.Dense(units=1, activation="sigmoid"))

# Compile neural network
network.compile(loss="binary_crossentropy", # Cross-entropy
                optimizer="rmsprop", # Root Mean Square Propagation
                metrics=["accuracy"]) # Accuracy performance metric

# Train neural network
history = network.fit(features_train, # Features
                      target_train, # Target vector
                      epochs=3, # Number of epochs
                      verbose=0, # No output
                      batch_size=100, # Number of observations per batch
                      validation_data=(features_test, target_test)) # Test data

Using TensorFlow backend.

Discussion

One strategy to combat overfitting neural networks is by penalizing the parameters (i.e., weights) of the neural network such that they are driven to be small values—creating a simpler model less prone to overfit. This method is called weight regularization or weight decay. More specifically, in weight regularization a penalty is added to the loss function, such as the L2 norm.

In Keras, we can add a weight regularization by including using kernel_regularizer=regularizers.l2(0.01) in a layer’s parameters. In this example, 0.01 determines how much we penalize higher parameter values.

Problem

You want to reduce overfitting.

Solution

Try stopping training when the test loss stops decreasing, a strategy called early stopping:

# Load libraries
import numpy as np
from keras.datasets import imdb
from keras.preprocessing.text import Tokenizer
from keras import models
from keras import layers
from keras.callbacks import EarlyStopping, ModelCheckpoint

# Set random seed
np.random.seed(0)

# Set the number of features we want
number_of_features = 1000

# Load data and target vector from movie review data
(data_train, target_train), (data_test, target_test) = imdb.load_data(
    num_words=number_of_features)

# Convert movie review data to a one-hot encoded feature matrix
tokenizer = Tokenizer(num_words=number_of_features)
features_train = tokenizer.sequences_to_matrix(data_train, mode="binary")
features_test = tokenizer.sequences_to_matrix(data_test, mode="binary")

# Start neural network
network = models.Sequential()

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=16,
                         activation="relu",
                         input_shape=(number_of_features,)))

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=16, activation="relu"))

# Add fully connected layer with a sigmoid activation function
network.add(layers.Dense(units=1, activation="sigmoid"))

# Compile neural network
network.compile(loss="binary_crossentropy", # Cross-entropy
                optimizer="rmsprop", # Root Mean Square Propagation
                metrics=["accuracy"]) # Accuracy performance metric

# Set callback functions to early stop training and save the best model so far
callbacks = [EarlyStopping(monitor="val_loss", patience=2),
             ModelCheckpoint(filepath="best_model.h5",
                             monitor="val_loss",
                             save_best_only=True)]

# Train neural network
history = network.fit(features_train, # Features
                      target_train, # Target vector
                      epochs=20, # Number of epochs
                      callbacks=callbacks, # Early stopping
                      verbose=0, # Print description after each epoch
                      batch_size=100, # Number of observations per batch
                      validation_data=(features_test, target_test)) # Test data

Using TensorFlow backend.

Discussion

As we discussed in Recipe 20.7, typically in the first training epochs both the training and test errors will decrease, but at some point the network will start “memorizing” the training data, causing the training error to continue to decrease even while the test error starts increasing. Because of this phenomenon, one of the most common and very effective methods to counter overfitting is to monitor the training process and stop training when the test error starts to increase. This strategy is called early stopping.

In Keras, we can implement early stopping as a callback function. Callbacks are functions that can be applied at certain stages of the training process, such as at the end of each epoch. Specifically, in our solution, we included EarlyStopping(monitor='val_loss', patience=2) to define that we wanted to monitor the test (validation) loss at each epoch and after the test loss has not improved after two epochs, training is interrupted. However, since we set patience=2, we won’t get the best model, but the model two epochs after the best model. Therefore, optionally, we can include a second operation, ModelCheckpoint, which saves the model to a file after every checkpoint (which can be useful in case a multiday training session is interrupted for some reason). It would be helpful for us, if we set save_best_only=True, because then ModelCheckpoint will only save the best model.

Problem

You want to reduce overfitting.

Solution

Introduce noise into your network’s architecture using dropout:

# Load libraries
import numpy as np
from keras.datasets import imdb
from keras.preprocessing.text import Tokenizer
from keras import models
from keras import layers

# Set random seed
np.random.seed(0)

# Set the number of features we want
number_of_features = 1000

# Load data and target vector from movie review data
(data_train, target_train), (data_test, target_test) = imdb.load_data(
    num_words=number_of_features)

# Convert movie review data to a one-hot encoded feature matrix
tokenizer = Tokenizer(num_words=number_of_features)
features_train = tokenizer.sequences_to_matrix(data_train, mode="binary")
features_test = tokenizer.sequences_to_matrix(data_test, mode="binary")

# Start neural network
network = models.Sequential()

# Add a dropout layer for input layer
network.add(layers.Dropout(0.2, input_shape=(number_of_features,)))

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=16, activation="relu"))

# Add a dropout layer for previous hidden layer
network.add(layers.Dropout(0.5))

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=16, activation="relu"))

# Add a dropout layer for previous hidden layer
network.add(layers.Dropout(0.5))

# Add fully connected layer with a sigmoid activation function
network.add(layers.Dense(units=1, activation="sigmoid"))

# Compile neural network
network.compile(loss="binary_crossentropy", # Cross-entropy
                optimizer="rmsprop", # Root Mean Square Propagation
                metrics=["accuracy"]) # Accuracy performance metric

# Train neural network
history = network.fit(features_train, # Features
                      target_train, # Target vector
                      epochs=3, # Number of epochs
                      verbose=0, # No output
                      batch_size=100, # Number of observations per batch
                      validation_data=(features_test, target_test)) # Test data

Using TensorFlow backend.

Discussion

Dropout is a popular and powerful method for regularizing neural networks. In dropout, every time a batch of observations is created for training, a proportion of the units in one or more layers is multiplied by zero (i.e., dropped). In this setting, every batch is trained on the same network (e.g., the same parameters), but each batch is confronted by a slightly different version of that network’s architecture.

Dropout is effective because by constantly and randomly dropping units in each batch, it forces units to learn parameter values able to perform under a wide variety of network architectures. That is, they learn to be robust to disruptions (i.e., noise) in the other hidden units, and this prevents the network from simply memorizing the training data.

It is possible to add dropout to both the hidden and input layers. When an input layer is dropped, its feature value is not introduced into the network for that batch. A common choice for the portion of units to drop is 0.2 for input units and 0.5 for hidden units.

In Keras, we can implement dropout by adding Dropout layers into our network architecture. Each Dropout layer will drop a user-defined hyperparameter of units in the previous layer every batch. Remember in Keras the input layer is assumed to be the first layer and not added using add. Therefore, if we want to add dropout to the input layer, the first layer we add in our network architecture is a dropout layer. This layer contains both the proportion of the input layer’s units to drop 0.2 and input_shape defining the shape of the observation data. Next, we add a dropout layer with 0.5 after each of the hidden layers.

Problem

Given a neural network that will take a long time to train, you want to save your progress in case the training process is interrupted.

Solution

Use the callback function ModelCheckpoint to save the model after every epoch:

# Load libraries
import numpy as np
from keras.datasets import imdb
from keras.preprocessing.text import Tokenizer
from keras import models
from keras import layers
from keras.callbacks import ModelCheckpoint

# Set random seed
np.random.seed(0)

# Set the number of features we want
number_of_features = 1000

# Load data and target vector from movie review data
(data_train, target_train), (data_test, target_test) = imdb.load_data(
    num_words=number_of_features)

# Convert movie review data to a one-hot encoded feature matrix
tokenizer = Tokenizer(num_words=number_of_features)
features_train = tokenizer.sequences_to_matrix(data_train, mode="binary")
features_test = tokenizer.sequences_to_matrix(data_test, mode="binary")

# Start neural network
network = models.Sequential()

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=16,
                         activation="relu",
                         input_shape=(number_of_features,)))

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=16, activation="relu"))

# Add fully connected layer with a sigmoid activation function
network.add(layers.Dense(units=1, activation="sigmoid"))

# Compile neural network
network.compile(loss="binary_crossentropy", # Cross-entropy
                optimizer="rmsprop", # Root Mean Square Propagation
                metrics=["accuracy"]) # Accuracy performance metric

# Set callback functions to early stop training and save the best model so far
checkpoint = [ModelCheckpoint(filepath="models.hdf5")]

# Train neural network
history = network.fit(features_train, # Features
                      target_train, # Target vector
                      epochs=3, # Number of epochs
                      callbacks=checkpoint, # Checkpoint
                      verbose=0, # No output
                      batch_size=100, # Number of observations per batch
                      validation_data=(features_test, target_test)) # Test data

Using TensorFlow backend.

Discussion

In Recipe 20.8 we used the callback function ModelCheckpoint in conjunction with EarlyStopping to end monitoring and end training when the test error stopped improving. However, there is another, more mundane reason for using ModelCheckpoint. In the real world, it is common for neural networks to train for hours or even days. During that time a lot can go wrong: computers can lose power, servers can crash, or inconsiderate graduate students can close your laptop.

ModelCheckpoint alleviates this problem by saving the model after every epoch. Specifically, after every epoch ModelCheckpoint saves a model to the location specified by the filepath parameter. If we include only a filename (e.g., models.hdf5) that file will be overridden with the latest model every epoch. If we only wanted to save the best model according to the performance of some loss function, we can set save_best_only=True and monitor='val_loss' to not override a file if the model has a worse test loss than the previous model. Alternatively, we can save every epoch’s model as its own file by including the epoch number and test loss score into the filename itself. For example, if we set filepath to model_{epoch:02d}_{val_loss:.2f}.hdf5, the name of the file containing the model saved after the 11th epoch with a test loss value of 0.33 would be model_10_0.35.hdf5 (notice that the epoch number is 0-indexed).

Problem

You want to evaluate a neural network using k-fold cross-validation.

Solution

Often k-fold cross-validating neural networks is neither necessary nor advisable. However, if it is appropriate: use Keras’ scikit-learn wrapper to allow Keras’ sequential models to use the scikit-learn API:

# Load libraries
import numpy as np
from keras import models
from keras import layers
from keras.wrappers.scikit_learn import KerasClassifier
from sklearn.model_selection import cross_val_score
from sklearn.datasets import make_classification

# Set random seed
np.random.seed(0)

# Number of features
number_of_features = 100

# Generate features matrix and target vector
features, target = make_classification(n_samples = 10000,
                                       n_features = number_of_features,
                                       n_informative = 3,
                                       n_redundant = 0,
                                       n_classes = 2,
                                       weights = [.5, .5],
                                       random_state = 0)

# Create function returning a compiled network
def create_network():

    # Start neural network
    network = models.Sequential()

    # Add fully connected layer with a ReLU activation function
    network.add(layers.Dense(units=16, activation="relu", input_shape=(
        number_of_features,)))

    # Add fully connected layer with a ReLU activation function
    network.add(layers.Dense(units=16, activation="relu"))

    # Add fully connected layer with a sigmoid activation function
    network.add(layers.Dense(units=1, activation="sigmoid"))

    # Compile neural network
    network.compile(loss="binary_crossentropy", # Cross-entropy
                    optimizer="rmsprop", # Root Mean Square Propagation
                    metrics=["accuracy"]) # Accuracy performance metric

    # Return compiled network
    return network

# Wrap Keras model so it can be used by scikit-learn
neural_network = KerasClassifier(build_fn=create_network,
                                 epochs=10,
                                 batch_size=100,
                                 verbose=0)

# Evaluate neural network using three-fold cross-validation
cross_val_score(neural_network, features, target, cv=3)

Using TensorFlow backend.

array([ 0.90461907,  0.77437743,  0.87068707])

Discussion

Theoretically, there is no reason we cannot use cross-validation to evaluate neural networks. However, neural networks are often used on very large data and can take hours or even days to train. For this reason, if the training time is long, adding the computational expense of k-fold cross-validation is unadvisable. For example, a model normally taking one day to train would take 10 days to evaluate using 10-fold cross-validation. If we have large data, it is often appropriate to simply evaluate the neural network on some test set.

If we have smaller data, k-fold cross-validation can be useful to maximize our ability to evaluate the neural network’s performance. This is possible in Keras because we can “wrap” any neural network such that it can use the evaluation features available in scikit-learn, including k-fold cross-validation. To accomplish this, we first have to create a function that returns a compiled neural network. Next we use KerasClassifier (if we have a classifier; if we have a regressor we can use KerasRegressor) to wrap the model so it can be used by scikit-learn. After this, we can use our neural network like any other scikit-learn learning algorithm (e.g., random forests, logistic regression). In our solution, we used cross_val_score to run a three-fold cross-validation on our neural network.

Problem

You want to automatically select the best hyperparameters for your neural network.

Solution

Combine a Keras neural network with scikit-learn’s model selection tools like GridSearchCV:

# Load libraries
import numpy as np
from keras import models
from keras import layers
from keras.wrappers.scikit_learn import KerasClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.datasets import make_classification

# Set random seed
np.random.seed(0)

# Number of features
number_of_features = 100

# Generate features matrix and target vector
features, target = make_classification(n_samples = 10000,
                                       n_features = number_of_features,
                                       n_informative = 3,
                                       n_redundant = 0,
                                       n_classes = 2,
                                       weights = [.5, .5],
                                       random_state = 0)

# Create function returning a compiled network
def create_network(optimizer="rmsprop"):

    # Start neural network
    network = models.Sequential()

    # Add fully connected layer with a ReLU activation function
    network.add(layers.Dense(units=16,
                             activation="relu",
                             input_shape=(number_of_features,)))

    # Add fully connected layer with a ReLU activation function
    network.add(layers.Dense(units=16, activation="relu"))

    # Add fully connected layer with a sigmoid activation function
    network.add(layers.Dense(units=1, activation="sigmoid"))

    # Compile neural network
    network.compile(loss="binary_crossentropy", # Cross-entropy
                    optimizer=optimizer, # Optimizer
                    metrics=["accuracy"]) # Accuracy performance metric

    # Return compiled network
    return network

# Wrap Keras model so it can be used by scikit-learn
neural_network = KerasClassifier(build_fn=create_network, verbose=0)

# Create hyperparameter space
epochs = [5, 10]
batches = [5, 10, 100]
optimizers = ["rmsprop", "adam"]

# Create hyperparameter options
hyperparameters = dict(optimizer=optimizers, epochs=epochs, batch_size=batches)

# Create grid search
grid = GridSearchCV(estimator=neural_network, param_grid=hyperparameters)

# Fit grid search
grid_result = grid.fit(features, target)

Using TensorFlow backend.

Discussion

In Recipes 12.1 and 12.2, we covered using scikit-learn’s model selection techniques to identify the best hyperparameters of a scikit-learn model. In Recipe 20.12 we learned that we can wrap our neural network so it can use the scikit-learn API. In this recipe we combine these two techniques to identify the best hyperparameters of a neural network.

The hyperparameters of a model are important and should be selected with care. However, before we get it into our heads that model selection strategies like grid search are a good idea, we must realize that if our model would normally have taken 12 hours or a day to train, this grid search process could take a week or more. Therefore, automatic hyperparameter tuning of neural networks is not the silver bullet, but it is a useful tool to have in certain circumstances.

In our solution we conducted a cross-validated grid search over a number of options for the optimization algorithm, number of epochs, and batch size. Even this toy example took a few minutes to run, but once it is done we can use best_params_ to view the hyperparameters of the neural network with the best results:

# View hyperparameters of best neural network
grid_result.best_params_

{'batch_size': 10, 'epochs': 5, 'optimizer': 'adam'}

Problem

You want to quickly visualize a neural network’s architecture.

Solution

Use Keras’ model_to_dot or plot_model:

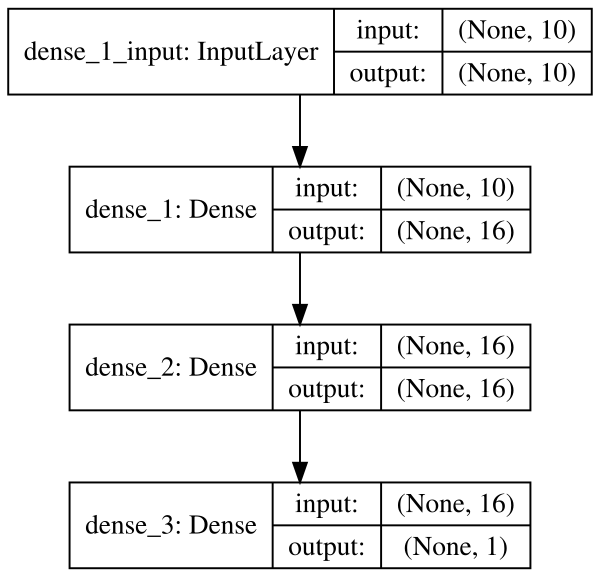
# Load libraries
from keras import models
from keras import layers
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
from keras.utils import plot_model

# Start neural network
network = models.Sequential()

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=16, activation="relu", input_shape=(10,)))

# Add fully connected layer with a ReLU activation function
network.add(layers.Dense(units=16, activation="relu"))

# Add fully connected layer with a sigmoid activation function
network.add(layers.Dense(units=1, activation="sigmoid"))

# Visualize network architecture
SVG(model_to_dot(network, show_shapes=True).create(prog="dot", format="svg"))

Using TensorFlow backend.

Alternatively, if we want to save the visualization as a file, we can use plot_model:

# Save the visualization as a file
plot_model(network, show_shapes=True, to_file="network.png")

Discussion

Keras provides utility functions to quickly visualize neural networks. If we wish to display a neural network in a Jupyter Notebook, we can use model_to_dot. The show_shapes parameter shows the shape of the inputs and outputs and can help with debugging. For a simpler model, we can set show_shapes=True:

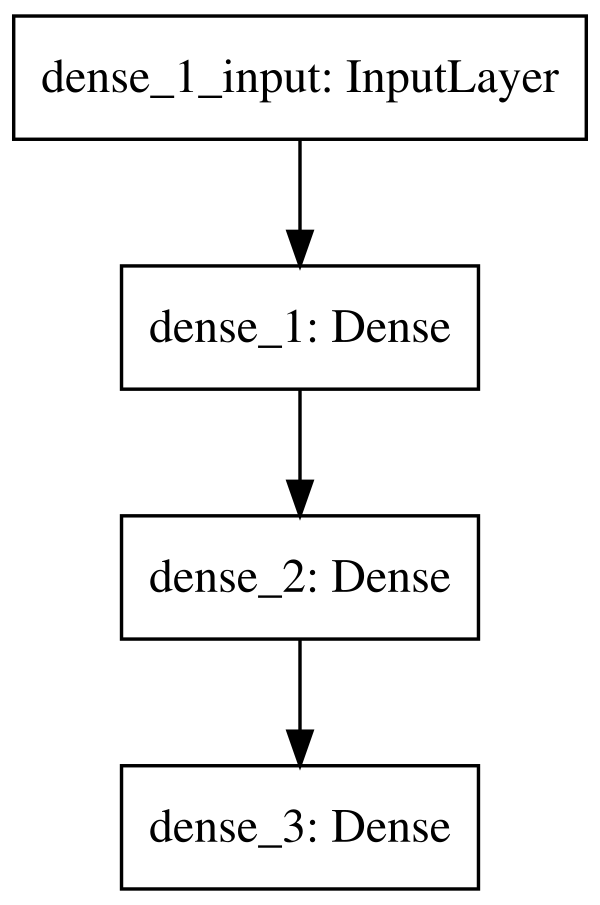
# Visualize network architecture
SVG(model_to_dot(network, show_shapes=False).create(prog="dot", format="svg"))

Problem

You want to classify images using a convolutional neural network.

Solution

Use Keras to create a neural network with at least one convolutional layer:

import numpy as np
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers.convolutional import Conv2D, MaxPooling2D
from keras.utils import np_utils
from keras import backend as K

# Set that the color channel value will be first
K.set_image_data_format("channels_first")

# Set seed
np.random.seed(0)

# Set image information
channels = 1
height = 28
width = 28

# Load data and target from MNIST data
(data_train, target_train), (data_test, target_test) = mnist.load_data()

# Reshape training image data into features
data_train = data_train.reshape(data_train.shape[0], channels, height, width)

# Reshape test image data into features
data_test = data_test.reshape(data_test.shape[0], channels, height, width)

# Rescale pixel intensity to between 0 and 1
features_train = data_train / 255
features_test = data_test / 255

# One-hot encode target
target_train = np_utils.to_categorical(target_train)
target_test = np_utils.to_categorical(target_test)
number_of_classes = target_test.shape[1]

# Start neural network
network = Sequential()

# Add convolutional layer with 64 filters, a 5x5 window, and ReLU activation function
network.add(Conv2D(filters=64,
                   kernel_size=(5, 5),
                   input_shape=(channels, width, height),
                   activation='relu'))

# Add max pooling layer with a 2x2 window
network.add(MaxPooling2D(pool_size=(2, 2)))

# Add dropout layer
network.add(Dropout(0.5))

# Add layer to flatten input
network.add(Flatten())

# # Add fully connected layer of 128 units with a ReLU activation function
network.add(Dense(128, activation="relu"))

# Add dropout layer
network.add(Dropout(0.5))

# Add fully connected layer with a softmax activation function
network.add(Dense(number_of_classes, activation="softmax"))

# Compile neural network
network.compile(loss="categorical_crossentropy", # Cross-entropy
                optimizer="rmsprop", # Root Mean Square Propagation
                metrics=["accuracy"]) # Accuracy performance metric

# Train neural network
network.fit(features_train, # Features
            target_train, # Target
            epochs=2, # Number of epochs
            verbose=0, # Don't print description after each epoch
            batch_size=1000, # Number of observations per batch
            validation_data=(features_test, target_test)) # Data for evaluation

Using TensorFlow backend.

<keras.callbacks.History at 0x133f37e80>

Discussion

Convolutional neural networks (also called ConvNets) are a popular type of network that has proven very effective at computer vision (e.g., recognizing cats, dogs, planes, and even hot dogs). It is completely possible to use feedforward neural networks on images, where each pixel is a feature. However, when doing so we run into two major problems. First, feedforward neural networks do not take into account the spatial structure of the pixels. For example, in a 10 × 10 pixel image we might convert it into a vector of 100 pixel features, and in this case feedforward would consider the first feature (e.g., pixel value) to have the same relationship with the 10th feature as the 11th feature. However, in reality the 10th feature represents a pixel on the far side of the image as the first feature, while the 11th feature represents the pixel immediately below the first pixel. Second, and relatedly, feedforward neural networks learn global relationships in the features instead of local patterns. In more practical terms, this means that feedforward neural networks are not able to detect an object regardless of where it appears in an image. For example, imagine we are training a neural network to recognize faces, and these faces might appear anywhere in the image from the upper right to the middle to the lower left.

The power of convolutional neural networks is their ability handle both of these issues (and others). A complete explanation of convolutional neural networks is well beyond the scope of this book, but a brief explanation will be useful. The data of an individual image contains two or three dimensions: height, width, and depth. The first two should be obvious, but the last deserves explanation. The depth is the color of a pixel. In grayscale images the depth is only one (the intensity of the pixel) and therefore the image is a matrix. However, in color images a pixel’s color is represented by multiple values. For example, in an RGB image a pixel’s color is represented by three values representing red, green, and blue. Therefore, the data for an image can be imagined to be a three-dimensional tensor: width × height × depth (called feature maps). In convolutional neural networks, a convolution (don’t worry if you don’t know what that means) can be imagined to slide a window over the pixels of an image, looking at both the individual pixel and also its neighbors. It then transforms the raw image data into a new three-dimensional tensor where the first two dimensions are approximately width and height, while the third dimension (which contained the color values) now represents the patterns—called filters—(for example, a sharp corner or sweeping gradient) to which that pixel “belongs.”

The second important concept for our purposes is that of pooling layers. Pooling layers move a window over our data (though usually they only look at every nth pixel, called striding) downsizing our data by summarizing the window in some way. The most common method is max pooling where the maximum value in each window is sent to the next layer. One reason for max pooling is merely practical; the convolutional process creates many more parameters to learn, which can get ungainly very quickly. Second, more intuitively, max pooling can be thought of as “zooming out” of an image.

An example might be useful here. Imagine we have an image containing a dog’s face. The first convolutional layer might find patterns like shape edges. Then we use a max pool layer to “zoom out,” and a second convolutional layer to find patterns like dog ears. Finally we use another max pooling layer to zoom out again and a final convolutional layer to find patterns like dogs’ faces.

Finally, fully connected layers are often used at the end of the network to do the actual classification.

While our solution might look like a lot of lines of code, it is actually very similar to our binary classifier from earlier in this chapter. In this solution we used the famous MNIST dataset, which is a de facto benchmark dataset in machine learning. The MNIST dataset contains 70,000 small images (28 × 28) of handwritten digits from 0 to 9. This dataset is labeled so that we know the actual digit (i.e., class) for each small image. The standard training-test split is to use 60,000 images for training and 10,000 for testing.

We reorganized the data into the format expected by a convolutional network. Specifically, we used reshape to convert the observation data such that it is the shape Keras expects. Next, we rescaled the values to be between 0 and 1, since training performance can suffer if an observation’s values are much greater than the network’s parameters (which are initialized as small numbers). Finally, we one-hot encoded the target data so that every observation’s target has 10 classes, representing the digits 0–9.

With the image data process we can build our convolutional network. First, we add a convolutional layer and specify the number of filters and other characteristics. The size of the window is a hyperparameter; however, 3 × 3 is standard practice for most images, while larger windows are often used in larger images. Second, we add a max pooling layer, summarizing the nearby pixels. Third, we add a dropout layer to reduce the chances of overfitting. Fourth, we add a flatten layer to convert the convolutionary inputs into a format able to be used by a fully connected layer. Finally, we add the fully connected layers and an output layer to do the actual classification. Notice that because this is a multiclass classification problem, we use the softmax activation function in the output layer.

It should be noted that this is a pretty simple convolutional neural network. It is common to see a much deeper network with many more convolutional and max pooling layers stacked together.

Problem

You want to improve the performance of your convolutional neural network.

Solution

For better results, preprocess the images and augment the data beforehand using ImageDataGenerator:

# Load library
from keras.preprocessing.image import ImageDataGenerator

# Create image augmentation
augmentation = ImageDataGenerator(featurewise_center=True, # Apply ZCA whitening
                                  zoom_range=0.3, # Randomly zoom in on images
                                  width_shift_range=0.2, # Randomly shift images
                                  horizontal_flip=True, # Randomly flip images
                                  rotation_range=90) # Randomly rotate

# Process all images from the directory 'raw/images'
augment_images = augmentation.flow_from_directory("raw/images", # Image folder
                                                  batch_size=32, # Batch size
                                                  class_mode="binary", # Classes
                                                  save_to_dir="processed/images")

Using TensorFlow backend.


Found 12665 images belonging to 2 classes.

Discussion

First an apology—this solution’s code will not immediately run for you because you do not have the required folders of images. However, since the most common situation is having a directory of images, I wanted to include it. The technique should easily translate to your own images.

One way to improve the performance of a convolutional neural network is to preprocess the images. We discussed a number of techniques in Chapter 8; however, it is worth noting that Keras’ ImageDataGenerator contains a number of basic preprocessing techniques. For example, in our solution we used featurewise_center=True to standardize the pixels across the entire data.

A second technique to improve performance is to add noise. An interesting feature of neural networks is that, counterintuitively, their performance often improves when noise is added to the data. The reason is that the additional noise can make the neural networks more robust in the face of real-world noise and prevents them from overfitting the data.

When training convolutional neural networks for images, we can add noise to our observations by randomly transforming images in various ways, such as flipping images or zooming in on images. Even small changes can significantly improve model performance. We can use the same ImageDataGenerator class to conduct these transformations. The Keras documentation (referenced in “See Also”) specifies the full list of available transformations; however, our example contains a sample of them are, including random zooming, shifting, flipping, and rotation.

It is important to note that the output of flow_from_directory is a Python generator object. This is because in most cases we will want to process the images on-demand as they are sent to the neural network for training. If we wanted to process all the images prior to training, we could simply iterate over the generator.

Finally, since augment_images is a generator, when training our neural network we will have to use fit_generator instead of fit. For example:

# Train neural network
network.fit_generator(augment_images,
                      #Number of times to call the generator for each epoch
                      steps_per_epoch=2000,
                      # Number of epochs
                      epochs=5,
                      # Test data generator
                      validation_data=augment_images_test,
                      # Number of items to call the generator
                      # for each test epoch
                      validation_steps=800)

Note all the raw images used in this recipe are available on GitHub.

See Also

• Image Preprocessing, Keras

Problem

You want to classify text data.

Solution

Use a long short-term memory recurrent neural network:

# Load libraries
import numpy as np
from keras.datasets import imdb
from keras.preprocessing import sequence
from keras import models
from keras import layers

# Set random seed
np.random.seed(0)

# Set the number of features we want
number_of_features = 1000

# Load data and target vector from movie review data
(data_train, target_train), (data_test, target_test) = imdb.load_data(
    num_words=number_of_features)

# Use padding or truncation to make each observation have 400 features
features_train = sequence.pad_sequences(data_train, maxlen=400)
features_test = sequence.pad_sequences(data_test, maxlen=400)

# Start neural network
network = models.Sequential()

# Add an embedding layer
network.add(layers.Embedding(input_dim=number_of_features, output_dim=128))

# Add a long short-term memory layer with 128 units
network.add(layers.LSTM(units=128))

# Add fully connected layer with a sigmoid activation function
network.add(layers.Dense(units=1, activation="sigmoid"))

# Compile neural network
network.compile(loss="binary_crossentropy", # Cross-entropy
                optimizer="Adam", # Adam optimization
                metrics=["accuracy"]) # Accuracy performance metric

# Train neural network
history = network.fit(features_train, # Features
                      target_train, # Target
                      epochs=3, # Number of epochs
                      verbose=0, # Do not print description after each epoch
                      batch_size=1000, # Number of observations per batch
                      validation_data=(features_test, target_test)) # Test data

Using TensorFlow backend.

Discussion

Oftentimes we have text data that we want to classify. While it is possible to use a type of convolutional network, we are going to focus on a more popular option: the recurrent neural network. The key feature of recurrent neural networks is that information loops back in the network. This gives recurrent neural networks a type of memory they can use to better understand sequential data. A popular type of recurrent neural network is the long short-term memory (LSTM) network, which allows for information to loop backward in the network. For a more detailed explanation, see the additional resources.

In this solution, we have our movie review data from Recipe 20.3 and we want to train an LSTM network to predict if these reviews are positive or negative. Before we can train our network, a little data processing is needed. Our text data comes in the form of a list of integers:

# View first observation
print(data_train[0])

[1, 14, 22, 16, 43, 530, 973, 2, 2, 65, 458, 2, 66, 2, 4, 173, 36, 256, 5, 25,
    100, 43, 838, 112, 50, 670, 2, 9, 35, 480, 284, 5, 150, 4, 172, 112, 167, 2,
    336, 385, 39, 4, 172, 2, 2, 17, 546, 38, 13, 447, 4, 192, 50, 16, 6, 147, 2,
    19, 14, 22, 4, 2, 2, 469, 4, 22, 71, 87, 12, 16, 43, 530, 38, 76, 15, 13, 2,
    4, 22, 17, 515, 17, 12, 16, 626, 18, 2, 5, 62, 386, 12, 8, 316, 8, 106, 5, 4,
    2, 2, 16, 480, 66, 2, 33, 4, 130, 12, 16, 38, 619, 5, 25, 124, 51, 36, 135,
    48, 25, 2, 33, 6, 22, 12, 215, 28, 77, 52, 5, 14, 407, 16, 82, 2, 8, 4, 107,
    117, 2, 15, 256, 4, 2, 7, 2, 5, 723, 36, 71, 43, 530, 476, 26, 400, 317, 46,
    7, 4, 2, 2, 13, 104, 88, 4, 381, 15, 297, 98, 32, 2, 56, 26, 141, 6, 194, 2,
    18, 4, 226, 22, 21, 134, 476, 26, 480, 5, 144, 30, 2, 18, 51, 36, 28, 224,
    92, 25, 104, 4, 226, 65, 16, 38, 2, 88, 12, 16, 283, 5, 16, 2, 113, 103, 32,
    15, 16, 2, 19, 178, 32]

Each integer in this list corresponds to some word. However, because each review does not contain the same number of words, each observation is not the same length. Therefore, before we can input this data into our neural network, we need to make all the observations the same length. We can do this using pad_sequences. pad_sequences pads each observation’s data so that they are all the same size. We can see this if we look at our first observation after it is processed by pad_sequences:

# View first observation
print(features_test[0])

[  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   1  89  27   2   2  17 199 132   5   2  16   2  24   8
 760   4   2   7   4  22   2   2  16   2  17   2   7   2   2   9   4   2
   8  14 991  13 877  38  19  27 239  13 100 235  61 483   2   4   7   4
  20 131   2  72   8  14 251  27   2   7 308  16 735   2  17  29 144  28
  77   2  18  12]

Next, we use one of the most promising techniques in natural language processing: word embeddings. In our binary classifier from Recipe 20.3, we one-hot encoded the observations and used that as inputs to the neural network. However, this time we will represent each word as a vector in a multidimensional space, and allow the distance between two vectors to represent the similarity between words. In Keras we can do this by adding an Embedding layer. For each value sent to the Embedding layer, it will output a vector representing that word. The following layer is our LSTM layer with 128 units, which allows for information from earlier inputs to be used in futures, directly addressing the sequential nature of the data. Finally, because this is a binary classification problem (each review is positive or negative), we add a fully connected output layer with one unit and a sigmoid activation function.

It is worth noting that LSTMs are a very broad topic and the focus of much research. This recipe, while hopefully useful, is far from the last word on the implementation of LSTMs.