Table of Contents for

21st Century C

As a warm-up, let’s shave a line off of every program you write.

Your program must have a main function, and it has to be of return type int, so you must absolutely have the following in your program:

int main(){ ... }

You would think that you therefore have to have a return statement that indicates what integer gets returned by main. However, the C standard knows how infrequently this is used and lets you not bother: “… reaching the } that terminates the main function returns a value of 0” (C99 & C11 §5.1.2.2(3)). That is, if you don’t write return 0; as the last line of your program, then it will be assumed.

Recall that, after running your program, you can use echo $? to see its return value; you can use this to verify that programs that reach the end of main do indeed always return zero.

Earlier, I showed you this version of hello.c, and you can now see how I got away with a main containing only one #include plus one line of code:^[8]

#include <stdio.h>
int main(){ printf("Hello, world.\n"); }

Think back to the last time you read a play. At the beginning of the text, there was the Dramatis Personæ, listing the characters. A list of character names probably didn’t have much meaning to you before you started reading, so if you’re like me you skipped that page and went straight to the start of the play. When you are in the thick of the plot and you forget who Benvolio is, it’s nice to be able to flip back to the head of the play and get a one-line description (he is Romeo’s friend and Montague’s nephew), but that’s because you’re reading on paper. If the text were on a screen, you could search for Benvolio’s first appearance.

In short, the Dramatis Personæ is not very useful to readers. It would be better to introduce characters when they first appear.

I see code like this pretty often:

#include <stdio.h>

int main(){
    char *head;
    int i;
    double ratio, denom;

    denom=7;
    head = "There is a cycle to things divided by seven.";
    printf("%s\n", head);
    for (i=1; i<= 6; i++){
        ratio = i/denom;
        printf("%g\n", ratio);
    }
}

It has three or four lines of introductory material (I’ll let you decide how to count the whitespace), followed by the routine.

This is a throwback to ANSI C89, which required all declarations to be at the head of the block, due to technical limitations of early compilers. We still have to declare our variables, but we can minimize burden on the author and the reader by doing so at the first use:

#include <stdio.h>

int main(){
    double denom = 7;
    char *head = "There is a cycle to things divided by seven.";
    printf("%s\n", head);
    for (int i=1; i<= 6; i++){
        double ratio = i/denom;
        printf("%g\n", ratio);
    }
}

Here, the declarations happen as needed, so the onus of declaration reduces to sticking a type name before the first use. If you have color syntax highlighting, then the declarations are still easy to spot (and if you don’t have a text editor that supports color, you are seriously missing out—and there are dozens to hundreds to choose from!).

When reading unfamiliar code, my first instinct when I see a variable is to go back and see where it was declared. If the declaration is at the first use or the line immediately before the first use, I’m saved from a few seconds of skimming back. Also, by the rule that you should keep the scope of a variable as small as possible, we’re pushing the active variable count on earlier lines that much lower, which might start to matter for a longer function.

In this example, the declarations are at the beginning of their respective block, followed by nondeclaration lines. This is just how the example turned out, but you can freely intermix declarations and nondeclarations.

I left the declaration of denom at the head of the function, but we could move that into the loop as well (because it is only used inside the loop). We can trust that the compiler will know enough not to waste time and energy deallocating and reallocating the variable on every iteration of the loop [although this is what it theoretically does—see C99 & C11 §6.8(3)]. As for the index, it’s a disposable convenience for the loop, so it’s natural to reduce its scope to exactly the scope of the loop.

pthread_t *threads;
int thread_count;
thread_count = atoi(argv[1]);
threads = malloc(thread_count * sizeof(pthread_t));
...

free(threads);

int thread_count = atoi(argv[1]);
pthread_t threads[thread_count];
...

In the 1970s and 1980s, malloc returned a char* pointer and had to be cast (unless you were allocating a string), with a form like:

//don't bother with this sort of redundancy:
double* list = (double*) malloc(list_length * sizeof(double));

You don’t have to do this anymore, because malloc now gives you a void pointer, which the compiler will comfortably autocast to anything. The easiest way to do the cast is to declare a new variable with the right type. For example, functions that have to take in a void pointer will typically begin with a form like:

int use_parameters(void *params_in){
    param_struct *params = params_in;   //Effectively casting pointer-to-NULL
    ...                                 //to a pointer-to-param_struct. 
}

More generally, if it’s valid to assign an item of one type to an item of another type, then C will do it for you without your having to tell it to with an explicit cast. If it’s not valid for the given type, then you’ll have to write a function to do the conversion anyway.This isn’t true of C++, which depends more on types and therefore requires every cast to be explicit.

There remain two reasons to use C’s type-casting syntax to cast a variable from one type to another.

First, when dividing two numbers, an integer divided by an integer will always return an integer, so the following statements will both be true:

4/2 == 2;
3/2 == 1;

That second one is the source of lots of errors. It’s easy to fix: if i is an integer, then i + 0.0 is a floating-point number that matches the integer. Don’t forget parentheses as needed, but that solves your problem. If you have a constant, 2 is an integer and 2.0 or even just 2. is floating point. Thus, all of these variants work:

int two=2;
3/(two+0.0) == 1.5;
3/(2+0.0) == 1.5;
3/2.0 == 1.5;
3/2. == 1.5;

You can also use the casting form:

3/(double)two == 1.5;
3/(double)2 == 1.5;

I’m partial to the add-zero form, for æsthetic reasons; you’re welcome to prefer the cast-to-double form. But make a habit of one or the other every time you reach for that / key, because this is the source of many, many errors (and not just in C; lots of other languages also like to insist that int / int ⇒ int—not that that makes it OK).

Second, array indices have to be integers. It’s the law [C99 and C11 §6.5.2.1(1)], and gcc will complain if you send a floating-point index. So, you may have to cast to an integer, even if you know that in your situation you will always have an integer-valued expression.

4/(double)2 == 2.0;         //This is floating-point, not an int.
mylist[4/(double)2];        //So, an error: floating-point index

mylist[(int)(4/(double)2)]; //Works. Take care with the parens.

int index=4/(double)2;      //This form also works, and is more legible. 
mylist[index];

You can see that even for the few legitimate reasons to cast, you have options to avoid the casting syntax: adding 0.0 and declaring an integer variable for your array indices. Bear in mind the existence of the casting form var_type2 = (type2) var_type1, because it might come in handy some day, and in a few chapters, we’ll get to compound literals that mimic this form. But there are always less redundant and easier to read alternatives to explicit type casting.

Enums are a good idea that went bad.

The benefit is clear enough: integers are not at all mnemonic, and so wherever you are about to put a short list of integers in your code, you are better off naming them. Here’s the even worse means of how we could do it without the enum keyword:

#define NORTH 0
#define SOUTH 1
#define EAST 2
#define WEST 3

With enum, we can shrink that down to one line of source code, and our debugger is more likely to know what EAST means. Here’s the improvement over the sequence of #defines:

enum directions {NORTH, SOUTH, EAST, WEST};

But we now have five new symbols in our namespaces: directions, NORTH, SOUTH, EAST, and WEST.

For an enum to be useful, it typically has to be global (i.e., declared in a header file intended to be included in many places all over a project). For example, you’ll often find enums typedefed in the public header file for a library. To minimize the chance of name clashes, library authors use names like G_CONVERT_ERROR_NOT_ABSOLUTE_PATH or the relatively brief CblasConjTrans.

At that point, an innocuous and sensible idea has fallen apart. I don’t want to type these messes, and I use them so infrequently that I have to look them up every time (especially because many are infrequently used error values or input flags, so there’s typically a long gap between each use). Also, all caps reads like yelling.

My own habit is to use single characters, wherein I would mark transposition with 't' and a path error with 'p'. I think this is enough to be mnemonic—in fact, I’m far more likely to remember how to spell 'p' than how to spell that all-caps mess—and it requires no new entries in the namespace.

I think usability considerations trump efficiency issues at this level, but even so, bear in mind that an enumeration is typically an integer, and char is C-speak for a single byte. So when comparing enums, you will likely need to compare the states of 16 bits or more, whereas with a char, you need compare only 8. So even if the speed argument were relevant, it would advocate against enums.

We sometimes need to combine flags. When opening a file using the open system call, you might need to send O_RDWR|O_CREAT, which is the bitwise combination of the two enums. You probably don’t use open directly all that often; you are probably making more use of fopen, which is more user friendly. Instead of using an enum, it uses a one- or two-letter string, like "r" or "r+", to indicate whether something is readable, writeable, both, et cetera.

In the context, you know "r" stands for read, and if you don’t have the convention memorized, you can confidently expect that you will after a few more uses of fopen, whereas I still have to check whether I need CblasTrans or CBLASTrans or CblasTranspose every time.

On the plus side of enums, you have a small, fixed set of symbols, so if you mistype one, the compiler stops and forces you to fix your typo. With strings, you won’t know you had a typo until runtime. Conversely, strings are not a small, fixed set of symbols, so you can more easily extend the set of enums. For example, I once ran into an error handler that offers itself for use by other systems—as long as the errors the new system generates match the handful of errors in the original system’s enum. If the errors were short strings, extension by others would be trivial.

There are reasons for using enums: sometimes you have an array that makes no sense as a struct but that nonetheless requires named elements, and when doing kernel-level work, giving names to bit patterns is essential. But in cases where enums are used to indicate a short list of options or a short list of error codes, a single character or a short string can serve the purpose without cluttering up the namespace or users’ memory.

In the olden days, assembly code didn’t have the modern luxuries of while and for loops. Instead, there were only conditions, labels, and jumps. Where we would write while (a[i] < 100) i++;, our ancestors might have written:

label 1
if a[i] >= 100
    go to label 2
increment i
go to label 1
label 2

If it took you a minute to follow what was going on in this block, imagine reading this in a real-world situation, where the loop would be interspersed, nested, or half-nested with other jumps. I can attest from my own sad and painful experience that following the flow of such code is basically impossible, which is why goto is considered harmful in the present day [Dijkstra 1968].

You can see how welcome C’s while keyword would have been to somebody stuck writing in assembly code all day. However, there is a subset of C that is still built around labels and jumps, including the syntax for labels, goto, switch, case, default, break, and continue. I personally think of this as the portion of C that is transitional from how authors of assembly code wrote to the more modern style. This segment will present these forms as such, and suggest when they are still useful. However, this entire subset of the language is technically optional, in the sense that you can write equivalent code using the rest of the language.

/* Sum to the first NaN in the vector.
  Sets error to zero on a clean summation, 1 if a NaN is hit.*/
double sum_to_first_nan(double* vector, int vector_size,
                     double* vector2, int vector2_size, int *error){
    double sum=0;
    *error=1;
    for (int i=0; i< vector_size; i++){
        if (isnan(vector[i])) goto outro;
        sum += vector[i];
    }

    for (int i=0; i< vector2_size; i++){
        if (isnan(vector2[i])) goto outro;
        sum += vector2[i];
    }
    *error=0;

    outro:
    printf("The sum until the first NaN (if any) was %g\n", sum);
    free(vector);
    free(vector2);
    return sum;
}

char c;
while ((c = getopt(...))){
    switch(c){
       case 'v':
            verbose++;
            break;
       case 'w':
            weighting_function();
            break;
       case 'f':
            fun_function();
            break;
    }
}

char c;
while ((c = getopt(...))){
    if (c == 'v')      verbose++;
    else if (c == 'w') weighting_function();
    else if (c == 'f') fun_function();
}

#include <stdio.h>
#include <math.h> //isnan

double ref;

double set_na(){
    if (!ref) {
        ref=0/0.;                   
        char *cr = (char *)(&ref);  
        cr[2]='a';                  
    }
    return ref;
}

int is_na(double in){               
    if (!ref) return 0;  //set_na was never called==>no NAs yet.

    char *cc = (char *)(&in);
    char *cr = (char *)(&ref);
    for (int i=0; i< sizeof(double); i++)
        if (cc[i] != cr[i]) return 0;
    return 1;
}

int main(){
    double x = set_na();
    double y = x;
    printf("Is x=set_na() NA? %i\n", is_na(x));
    printf("Is x=set_na() NAN? %i\n", isnan(x));
    printf("Is y=x NA? %i\n", is_na(y));
    printf("Is 0/0 NA? %i\n", is_na(0/0.));
    printf("Is 8 NA? %i\n", is_na(8));
}

Floating-point math is challenging in surprising places. It’s easy to write down a reasonable algorithm that introduces 0.01% error on every step, which over 1,000 iterations turns the results into complete slop. You can easily find volumes filled with advice about how to avoid such surprises. Much of it is still valid today, but much of it is easy to handle quickly: use double instead of float, and for intermediate values in calculations, it doesn’t hurt to use long double.

For example, Writing Scientific Software advises users to avoid what they call the single-pass method of calculating variances ([Oliveira 2006] p. 24). They give an example that is ill-conditioned. As you may know, a floating-point number is so named because the decimal floats to the right position in an otherwise scale-independent number. For exposition, let’s pretend the computer works in decimal; then this sort of system can store 23,000,000 exactly as easily as it could store .23 or .00023—just let the decimal point float. But 23,000,000.00023 is a challenge, because there are only so many digits available for expressing the prefloat value, as shown in Example 7-3.

#include <stdio.h>

int main(){
    printf("%f\n", (float)333334126.98);
    printf("%f\n", (float)333334125.31);
}

The output from Example 7-3 on my netbook, with a 32-bit float:

333334112.000000
333334112.000000

There went our precision. This is why computing books from times past worried so much about writing algorithms to minimize the sort of drift one could have with only seven reliable decimal digits.

That’s for a 32-bit float, which is the minimum standard anymore. I even had to explicitly cast to float, because the system will otherwise store these numbers with a 64-bit value.

64 bits is enough to reliably store 15 significant digits: 100,000,000,000,001 is not a problem. (Try it! Hint: printf(%.20g, val) prints val to 20 significant decimal digits).

Example 7-4 presents the code to run Oliveira and Stewart’s example, including a single-pass calculation of mean and variance. Once again, this code is only useful as a demonstration, because the GSL already implements means and variance calculators. It does the example twice: once with the ill-conditioned version, which gave our authors from 2006 terrible results, and once after subtracting 34,120 from every number, which thus gives us something that even a plain float can handle with full precision. We can be confident that the results using the not-ill-conditioned numbers are accurate.

#include <math.h>
#include <stdio.h> //size_t

typedef struct meanvar {double mean, var;} meanvar;

meanvar mean_and_var(const double *data){
    long double avg = 0,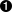                                  
          avg2 = 0;
    long double ratio;
    size_t cnt= 0;
    for(size_t i=0;  !isnan(data[i]); i++){
        ratio = cnt/(cnt+1.0);
        cnt   ++;
        avg   *= ratio;
        avg2  *= ratio;
        avg   += data[i]/(cnt +0.0);
        avg2  += pow(data[i], 2)/(cnt +0.0);
    }
    return (meanvar){.mean = avg,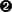                         
                    .var = avg2 - pow(avg, 2)}; //E[x^2] - E^2[x]
}

int main(){
    double d[] = { 34124.75, 34124.48,
                   34124.90, 34125.31,
                   34125.05, 34124.98, NAN};

    meanvar mv = mean_and_var(d);
    printf("mean: %.10g var: %.10g\n", mv.mean, mv.var*6/5.);

    double d2[] = { 4.75, 4.48,
                    4.90, 5.31,
                    5.05, 4.98, NAN};

    mv = mean_and_var(d2);
    mv.var *= 6./5;                                       
    printf("mean: %.10g var: %.10g\n", mv.mean, mv.var);  
}

Here are the results:

mean: 34124.91167 var: 0.07901676614
mean: 4.911666667 var: 0.07901666667

The means are off by 34,120, because we set up the calculations that way, but are otherwise precisely identical (the .66666 would continue off the page if we let it), and the ill-conditioned variance is off by 0.000125%. The ill-conditioning had no appreciable effect.

That, dear reader, is technological progress. All we had to do was throw twice as much space at the problem, and suddenly all sorts of considerations are basically irrelevant. You can still construct realistic cases where numeric drift can create problems, but it’s much harder to do so. Even if there is a perceptible speed difference between a program written with all doubles and one written with all floats, it’s worth extra microseconds to be able to ignore so many caveats.

Should we use long ints everywhere integers are used? The case isn’t quite as open and shut. A double representation of π is more precise than a float representation of π, even though we’re in the ballpark of three; both int and long int representations of numbers up to a few billion are precisely identical. The only issue is overflow. There was once a time when the limit was scandalously short, like around 32,000. It’s good to be living in the present, where the range of integers on a typical system might go up to about ±2.1 billion. But if you think there’s even a remote possibility that you have a variable that might multiply its way up to the billions (that’s just 200 × 200 × 100 × 500, for example), then you certainly need to use a long int or even a long long int, or else your answer won’t just be imprecise—it’ll be entirely wrong, as C suddenly wraps around from +2.1 billion to -2.1 billion. Have a look at your copy of limits.h (typically in the usual locations like /include or /usr/include/) for details; on my netbook, for example, limits.h says that int and long int are identical.

If you are doing some serious counting, then #include <stdint.h> and use the intmax_t type, which is guaranteed to have a range at least up to 2⁶³-1 = 9,223,372,036,854,775,807 (C99 §7.18.1 & C11 §7.20.1).

If you do switch, remember that you’ll need to modify all your printfs to use %li as the format specifier for long int and %ji for intmax_t.

Here is a simple program that compares an int to a size_t, which is an unsigned integer representing a memory address (formally, it is what sizeof returns):

#include <stdio.h>

int main(){
    int neg = -2;
    size_t zero = 0;
    if (neg < zero) printf("Yes, -2 is less than 0.\n");
    else            printf("No, -2 is not less than 0.\n");
}

You can run this and verify that it gets the wrong answer. This snippet demonstrates that in most comparisons between signed and an unsigned integers, C will force the signed type to unsigned (C99 & C11 §6.3.1.8(1)), which is the opposite of what we as humans expect. I will admit to having been caught by this a few times, and it is hard to spot the bug because the comparison looks so natural.

C gives you a multitude of ways to represent a number, from unsigned short int up to long double. This section and the last advise against using them all. Micromanaging the types, using float for efficiency and breaking out double for special occasions, or using unsigned int because you are confident the variable will never store a negative number, opens the way to bugs caused by subtle numeric imprecision and C’s not-quite-intuitive arithmetic conversions.