Special Syntax for Strings

The String class is handled in a somewhat special way by the Java language. This is because, despite not being a primitive type, strings are so common that it makes sense for Java to have a number of special syntax features designed to make handling strings easy. Let’s look at some examples of special syntax features for strings that Java provides.

String pet = "Cat";

char[] pullingTeeth = {'C', 'a', 't'};
String pet = new String(pullingTeeth);

System.out.println("Dog".length());

    public void println(Object x) {
        String s = String.valueOf(x);
        synchronized (this) {
            print(s);
            newLine();
        }
    }

    public static String valueOf(Object obj) {
        return (obj == null) ? "null" : obj.toString();
    }

String s1 = "AB";
String s2 = "CD";

String s3 = s1;
System.out.println(s1 == s3); // Same object?

s3 = s1 + s2;
System.out.println(s1 == s3); // Still same?
System.out.println(s1);
System.out.println(s3);

String Immutability

In order to “change” a string, as we saw when we discussed string concatenation, we actually need to create an intermediate StringBuilder object to act as a temporary scratch area, and then call toString() on it, to bake it into a new instance of String. Let’s see how this works in code:

String pet = "Cat";
StringBuilder sb = new StringBuilder(pet);
sb.append("amaran");
String boat = sb.toString();
System.out.println(boat);

Code like this behaves equivalently to the following, although in Java 9 and above the actual bytecode sequences will differ:

String pet = "Cat";
String boat = pet + "amaran";
System.out.println(boat);

Of course, as well as being used under the hood by javac, the StringBuilder class can also be used directly in application code, as we’ve seen.

String immutability is an extremely useful language feature. For example, suppose the + changed a string instead of creating a new one; then, whenever any thread concatenated two strings together, all other threads would also see the change. This is unlikely to be a useful behavior for most programs, and so immutability makes good sense.

    public int hashCode() {
        int h = hash;
        if (h == 0 && value.length > 0) {
            char val[] = value;

            for (int i = 0; i < value.length; i++) {
                h = 31 * h + val[i];
            }
            hash = h;
        }
        return h;
    }

Regular Expressions

Java has support for regular expressions (often shortened to regex or regexp). These are a representation of a search pattern used to scan and match text. A regex is a sequence of characters that we want to search for. They can be very simple—for example, abc means that we’re looking for a, followed immediately by b, followed immediately by c, anywhere within the text we’re searching through. Note that a search pattern may match an input text in zero, one, or more places.

The simplest regexes are just sequences of literal characters, like abc. However, the language of regexes can express more complex and subtle ideas than just literal sequences. For example, a regex can represent patterns to match like:

• A numeric digit

• Any letter

• Any number of letters, which must all be in the range a to j but can be upper- or lowercase

• a followed by any four characters, followed by b

The syntax we use to write regular expressions is simple, but because we can build up complex patterns, it is often possible to write an expression that does not implement precisely what we wanted. When using regexes, it is very important to always test them fully. This should include both test cases that should pass and cases that should fail.

To express these more complex patterns, regexes use metacharacters. These are special characters that indicate that special processing is required. This can be thought of as similar to the use of the * character in operating system shells. In those circumstances, it is understood that the * is not to be interpreted literally but instead means “anything.” If we wanted to list all the Java source files in the current directory on Unix, we would issue the command:

ls *.java

The metacharacters of regexes are similar, but there are far more of them, and they are far more flexible than the set available in shells. They also have different meanings than they do in shell scripts, so don’t get confused.

Let’s meet a couple of examples. Suppose we want to have a spell-checking program that is relaxed about the difference in spelling between British and American English. This means that honor and honour should both be accepted as valid spelling choices. This is easy to do with regular expressions.

Java uses a class called Pattern (from the package java.util.regex) to represent a regex. This class can’t be directly instantiated, however. Instead, new instances are created by using a static factory method, compile(). From a pattern, we then derive a Matcher for a particular input string that we can use to explore the input string. For example, let’s examine a bit of Shakespeare from the play Julius Caesar:

Pattern p = Pattern.compile("honou?r");

String caesarUK = "For Brutus is an honourable man";
Matcher mUK = p.matcher(caesarUK);

String caesarUS = "For Brutus is an honorable man";
Matcher mUS = p.matcher(caesarUS);

System.out.println("Matches UK spelling? " + mUK.find());
System.out.println("Matches US spelling? " + mUS.find());

The last example introduces our first regex metacharacter ?, in the pattern honou?r. This means “the preceding character is optional”—so both honour and honor will match. Let’s look at another example. Suppose we want to match both minimize and minimise (the latter spelling is more common in British English). We can use square brackets to indicate that any character from a set (but only one alternative) [] can be used—like this:

Pattern p = Pattern.compile("minimi[sz]e");

Table 9-1 provides an expanded list of metacharacters available for Java regexes.

There are a few more, but this is the basic list, and from this, we can construct more complex expressions for matching such as the examples given earlier in this section:

// Note that we have to use \\ because we need a literal \
// and Java uses a single \ as an escape character
String pStr = "\\d"; // A numeric digit
String text = "Apollo 13";
Pattern p = Pattern.compile(pStr);
Matcher m = p.matcher(text);
System.out.print(pStr + " matches " + text + "? " + m.find());
System.out.println(" ; match: " + m.group());


pStr = "[a..zA..Z]"; //Any letter
p = Pattern.compile(pStr);
m = p.matcher(text);
System.out.print(pStr + " matches " + text + "? " + m.find());
System.out.println(" ; match: " + m.group());

// Any number of letters, which must all be in the range 'a' to 'j'
// but can be upper- or lowercase
pStr = "([a..jA..J]*)";
p = Pattern.compile(pStr);
m = p.matcher(text);
System.out.print(pStr + " matches " + text + "? " + m.find());
System.out.println(" ; match: " + m.group());

text = "abacab";
// 'a' followed by any four characters, followed by 'b'
pStr = "a....b";
p = Pattern.compile(pStr);
m = p.matcher(text);
System.out.print(pStr + " matches " + text + "? " + m.find());
System.out.println(" ; match: " + m.group());

Let’s conclude our quick tour of regular expressions by meeting a new method that was added to Pattern as part of Java 8: asPredicate(). This method is present to allow us to easily bridge from regular expressions to the Java Collections and their new support for lambda expressions.

For example, suppose we have a regex and a collection of strings. It’s very natural to ask the question: “Which strings match against the regex?” We do this by using the filter idiom, and by converting the regex to a Predicate using the helper method, like this:

String pStr = "\\d"; // A numeric digit
Pattern p = Pattern.compile(pStr);

String[] inputs = {"Cat", "Dog", "Ice-9", "99 Luftballoons"};
List<String> ls = Arrays.asList(inputs);
List<String> containDigits = ls.stream()
                               .filter(p.asPredicate())
                               .collect(Collectors.toList());
System.out.println(containDigits);

Java’s built-in support for text processing is more than adequate for the majority of text processing tasks that business applications normally require. More advanced tasks, such as the search and processing of very large data sets, or complex parsing (including formal grammars) are outside the scope of this book, but Java has a large ecosystem of helpful libraries and bindings to specialized technologies for text processing and analysis.

How Java Represents Integer Types

Java’s integer types are all signed, as we first mentioned in “Primitive Data Types”. This means that all integer types can represent both positive and negative numbers. As computers work with binary, this means that the only really logical way to represent this is to split the possible bit patterns up and use half of them to represent negative numbers.

Let’s work with Java’s byte type to investigate how Java represents integers. This has 8 bits, so can represent 256 different numbers (i.e., 128 negative and 128 non-negative numbers). It’s logical to use the pattern 0b0000_0000 to represent zero (recall that Java has the syntax 0b<binary digits> to represent numbers as binary), and then it’s easy to figure out the bit patterns for the positive numbers:

byte b = 0b0000_0001;
System.out.println(b); // 1

b = 0b0000_0010;
System.out.println(b); // 2

b = 0b0000_0011;
System.out.println(b); // 3

// ...

b = 0b0111_1111;
System.out.println(b); // 127

When we set the first bit of the byte, the sign should change (as we have now used up all of the bit patterns that we’ve set aside for non-negative numbers). So the pattern 0b1000_0000 should represent some negative number—but which one?

Consider the bit pattern consisting of all set bits: 0b1111_1111. If we add 1 to this number, then the result will overflow the 8 bits of storage that a byte has, resulting in 0b1_0000_0000. If we want to constrain this to fit within the byte data type, then we should ignore the overflow, so this becomes 0b0000_0000, otherwise known as zero. It is therefore natural to adopt the representation that “all set bits is -1.” This allows for natural arithmetic behavior, like this:

b = (byte) 0b1111_1111; // -1
System.out.println(b);
b++;
System.out.println(b);

b = (byte) 0b1111_1110; // -2
System.out.println(b);
b++;
System.out.println(b);

Finally, let’s look at the number that 0b1000_0000 represents. It’s the most negative number that the type can represent, so for byte:

b = (byte) 0b1000_0000;
System.out.println(b); // -128

This representation is called two’s complement, and is the most common representation for signed integers. To use it effectively, there are only two points that you need to remember:

• A bit pattern of all 1’s is the representation for −1.

• If the high bit is set, the number is negative.

Java’s other integer types (short, int, and long) behave in very similar ways but with more bits in their representation. The char data type is different because it represents a Unicode character, but in some ways behaves as an unsigned 16-bit numeric type. It is not normally regarded as an integer type by Java programmers.

Java and Floating-Point Numbers

Computers represent numbers using binary. We’ve seen how Java uses the two’s complement representation for integers. But what about fractions or decimals? Java, like almost all modern programming languages, represents them using floating-point arithmetic. Let’s take a look at how this works, first in base-10 (regular decimal) and then in binary. Java defines the two most important mathematical constants, e and π (pi), as constants in java.lang.Math like this:

public static final double E = 2.7182818284590452354;
public static final double PI = 3.14159265358979323846;

Of course, these constants are actually irrational numbers and cannot be precisely expressed as a fraction, or by any finite decimal number.¹ This means that whenever we try to represent them in a computer, there is always rounding error. Let’s suppose we only want to deal with eight digits of π, and we want to represent the digits as a whole number. We can use a representation like this:

This starts to suggest the basis of how floating-point numbers work. We use some of the bits to represent the significant digits (314159265, in our example) of the number and some bits to represent the exponent of the base (-8, in our example). The collection of significant digits is called the significand and the exponent describes whether we need to shift the significand up or down to get to the desired number.

Of course, in the examples we’ve met until now, we’ve been working in base-10. Computers use binary, so we need to use this as the base in our floating-point examples. This introduces some additional complications.

Let’s look at an example that shows the rounding problem:

double d = 0.3;
System.out.println(d); // Special-cased to avoid ugly representation

double d2 = 0.2;
// Should be -0.1 but prints -0.09999999999999998
System.out.println(d2 - d);

The official standard that describes floating-point arithmetic is IEEE-754, and Java’s support for floating point is based on that standard. The standard uses 24 binary digits for standard precision and 53 binary digits for double precision.

As we mentioned briefly in Chapter 2, Java can be more accurate than the standard requires, by using hardware features if they are available. In extremely rare cases, usually where very strict compatability with other (possibly older) platforms is required, we can switch off this behavior by using strictfp to mandate perfect compliance with the IEEE-754 standard. This is almost never necessary and the vast majority of programmers will never need to use (or even see) this keyword.

double d = 0.3;
System.out.println(d);

BigDecimal bd = new BigDecimal(d);
System.out.println(bd);

bd = new BigDecimal("0.3");
System.out.println(bd);

bd = new BigDecimal(BigInteger.ONE);
bd.divide(new BigDecimal(3.0));
System.out.println(bd); // Should be 1/3

Java’s Standard Library of Mathematical Functions

To conclude this look at Java’s support for numeric data and math, let’s take a quick tour of the standard library of functions that Java ships with. These are mostly static helper methods that are located on the class java.lang.Math and include functions like:

abs()

Returns the absolute value of a number. Has overloaded forms for various primitive types.

Trigonometric functions

Basic functions for computing the sine, cosine, tangent, and so on. Java also includes hyperbolic versions and the inverse functions (such as arc sine).

max(), min()

Overloaded functions to return the greater and smaller of two arguments (both of the same numeric type).

floor()

Used to return the largest integer smaller than the argument (which is a double). ceil() returns the smallest integer larger than the argument.

pow(), exp(), log()

Functions for raising one number to the power of another, and for computing exponentials and natural logarithms. log10() provides logarithms to base-10, rather than the natural base.

Let’s look at some simple examples of how to use these functions:

System.out.println(Math.abs(2));
System.out.println(Math.abs(-2));

double cosp3 = Math.cos(0.3);
double sinp3 = Math.sin(0.3);
System.out.println((cosp3 * cosp3 + sinp3 * sinp3)); // Always 1.0

System.out.println(Math.max(0.3, 0.7));
System.out.println(Math.max(0.3, -0.3));
System.out.println(Math.max(-0.3, -0.7));

System.out.println(Math.min(0.3, 0.7));
System.out.println(Math.min(0.3, -0.3));
System.out.println(Math.min(-0.3, -0.7));

System.out.println(Math.floor(1.3));
System.out.println(Math.ceil(1.3));
System.out.println(Math.floor(7.5));
System.out.println(Math.ceil(7.5));

System.out.println(Math.round(1.3)); // Returns long
System.out.println(Math.round(7.5)); // Returns long

System.out.println(Math.pow(2.0, 10.0));
System.out.println(Math.exp(1));
System.out.println(Math.exp(2));
System.out.println(Math.log(2.718281828459045));
System.out.println(Math.log10(100_000));
System.out.println(Math.log10(Integer.MAX_VALUE));

System.out.println(Math.random());
System.out.println("Let's toss a coin: ");
if (Math.random() > 0.5) {
    System.out.println("It's heads");
} else {
    System.out.println("It's tails");
}

To conclude this section, let’s briefly discuss Java’s random() function. When this is first called, it sets up a new instance of java.util.Random. This is a pseudorandom number generator (PRNG)—a deterministic piece of code that produces numbers that look random but are actually produced by a mathematical formula.² In Java’s case, the formula used for the PRNG is pretty simple, for example:

    // From java.util.Random
    public double nextDouble() {
        return (((long)(next(26)) << 27) + next(27)) * DOUBLE_UNIT;
    }

If the sequence of pseudorandom numbers always starts at the same place, then exactly the same stream of numbers will be produced. To get around this problem, the PRNG is seeded by a value that should contain as much true randomness as possible. For this source of randomness for the seed value, Java uses a CPU counter value that is normally used for high-precision timing.

Now that we’ve looked at text and numeric data, let’s move on to look at another of the most frequently encountered kinds of data: date and time information.

Introducing the Java 8 Date and Time API

Java 8 introduces the new package java.time, which contains the core classes that most developers work with. It also contains four subpackages:

java.time.chrono

Alternative chronologies that developers using calendaring systems that do not follow the ISO standard will interact with. An example would be a Japanese calendaring system.

java.time.format

Contains the DateTimeFormatter used for converting date and time objects into a String and also for parsing strings into the data and time objects.

java.time.temporal

Contains the interfaces required by the core date and time classes and also abstractions (such as queries and adjusters) for advanced operations with dates.

java.time.zone

Classes used for the underlying time zone rules; most developers won’t require this package.

One of the most important concepts when representing time is the idea of an instantaneous point on the timeline of some entity. While this concept is well defined within, for example, Special Relativity, representing it within a computer requires us to make some assumptions. In Java 8, we represent a single point in time as an Instant, which has these key assumptions:

• We cannot represent more seconds than can fit into a long.

• We cannot represent time more precisely than nanosecond precision.

This means that we are restricting ourselves to modeling time in a manner that is consistent with the capabilities of current computer systems. However, there is another fundamental concept that should also be introduced.

An Instant is about a single event in space-time. However, it is far from uncommon for programmers to have to deal with intervals between two events, and so Java 8 also introduces the java.time.Duration class. This class ignores calendar effects that might arise (e.g., from daylight saving time). With this basic conception of instants and durations between events, let’s move on to unpack the possible ways of thinking about an instant.

The parts of a timestamp

In Figure 9-1, we show the breakdown of the different parts of a timestamp in a number of possible ways.

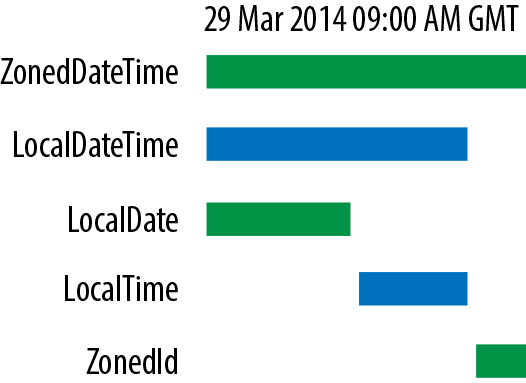
Figure 9-1. Breaking apart a timestamp

The key concept here is that there are a number of different abstractions that might be appropriate at different times. For example, there are applications where a LocalDate is key to business processing, where the needed granularity is a business day. Alternatively, some applications require subsecond, or even millisecond, precision. Developers should be aware of their domain and use a suitable representation within their application.

public class BirthdayDiary {
    private Map<String, LocalDate> birthdays;

    public BirthdayDiary() {
        birthdays = new HashMap<>();
    }

    public LocalDate addBirthday(String name, int day, int month,
                                 int year) {
        LocalDate birthday = LocalDate.of(year, month, day);
        birthdays.put(name, birthday);
        return birthday;
    }

    public LocalDate getBirthdayFor(String name) {
        return birthdays.get(name);
    }

    public int getAgeInYear(String name, int year) {
        Period period = Period.between(birthdays.get(name),
            birthdays.get(name).withYear(year));

        return period.getYears();
    }

    public Set<String> getFriendsOfAgeIn(int age, int year) {
        return birthdays.keySet().stream()
                .filter(p -> getAgeInYear(p, year) == age)
                .collect(Collectors.toSet());
    }

    public int getDaysUntilBirthday(String name) {
        Period period = Period.between(LocalDate.now(),
            birthdays.get(name));
        return period.getDays();
    }

    public Set<String> getBirthdaysIn(Month month) {
        return birthdays.entrySet().stream()
                .filter(p -> p.getValue().getMonth() == month)
                .map(p -> p.getKey())
                .collect(Collectors.toSet());
    }

    public Set<String> getBirthdaysInCurrentMonth() {
        return getBirthdaysIn(LocalDate.now().getMonth());
    }

    public int getTotalAgeInYears() {
        return birthdays.keySet().stream()
                .mapToInt(p -> getAgeInYear(p,
                      LocalDate.now().getYear()))
                .sum();
    }
}

Queries

Under a wide variety of circumstances we may find ourselves wanting to answer a question about a particular temporal object. Some example questions we may want answers to are:

• Is the date before March 1st?

• Is the date in a leap year?

• How many days is it from today until my next birthday?

This is achieved by the use of the TemporalQuery interface, which is defined like this:

public interface TemporalQuery<R> {
    R queryFrom(TemporalAccessor temporal);
}

The parameter to queryFrom() should not be null, but if the result indicates that a value was not found, null could be used as a return value.

Let’s look at an example of a query in action, by considering a query that answers the following question: “Which quarter of the year is this date in?” Java 8 does not support the concept of a quarter directly. Instead, code like this is used:

LocalDate today = LocalDate.now();
Month currentMonth = today.getMonth();
Month firstMonthofQuarter = currentMonth.firstMonthOfQuarter();

This still doesn’t give quarter as a separate abstraction and instead special case code is still needed. So let’s slightly extend the JDK support by defining this enum type:

public enum Quarter {
    FIRST, SECOND, THIRD, FOURTH;
}

Now, the query can be written as:

public class QuarterOfYearQuery implements TemporalQuery<Quarter> {
    @Override
    public Quarter queryFrom(TemporalAccessor temporal) {
        LocalDate now = LocalDate.from(temporal);

        if(now.isBefore(now.with(Month.APRIL).withDayOfMonth(1))) {
            return Quarter.FIRST;
        } else if(now.isBefore(now.with(Month.JULY)
                               .withDayOfMonth(1))) {
            return Quarter.SECOND;
        } else if(now.isBefore(now.with(Month.NOVEMBER)
                               .withDayOfMonth(1))) {
            return Quarter.THIRD;
        } else {
           return Quarter.FOURTH;
        }
    }
}

TemporalQuery objects can be used directly or indirectly. Let’s look at an example of each:

QuarterOfYearQuery q = new QuarterOfYearQuery();

// Direct
Quarter quarter = q.queryFrom(LocalDate.now());
System.out.println(quarter);

// Indirect
quarter = LocalDate.now().query(q);
System.out.println(quarter);

Under most circumstances, it is better to use the indirect approach, where the query object is passed as a parameter to query(). This is because it is normally a lot clearer to read in code.

Adjusters

Adjusters modify date and time objects. Suppose, for example, that we want to return the first day of a quarter that contains a particular timestamp:

public class FirstDayOfQuarter implements TemporalAdjuster {
    @Override
    public Temporal adjustInto(Temporal temporal) {

        final int currentQuarter = YearMonth.from(temporal)
                .get(IsoFields.QUARTER_OF_YEAR);

        switch (currentQuarter) {
            case 1:
                return LocalDate.from(temporal)
                        .with(TemporalAdjusters.firstDayOfYear());
            case 2:
                return LocalDate.from(temporal)
                        .withMonth(Month.APRIL.getValue())
                        .with(TemporalAdjusters.firstDayOfMonth());
            case 3:
                return LocalDate.from(temporal)
                        .withMonth(Month.JULY.getValue())
                        .with(TemporalAdjusters.firstDayOfMonth());
            case 4:
                return LocalDate.from(temporal)
                        .withMonth(Month.OCTOBER.getValue())
                        .with(TemporalAdjusters.firstDayOfMonth());
            default:
                return null; // Will never happen
        }
    }
}

Let’s look at an example of how to use an adjuster:

LocalDate now = LocalDate.now();
Temporal fdoq = now.with(new FirstDayOfQuarter());
System.out.println(fdoq);

The key here is the with() method, and the code should be read as taking in one Temporal object and returning another object that has been modified. This is completely usual for APIs that work with immutable objects.

Legacy Date and Time

Unfortunately, many applications are not yet converted to use the superior date and time libraries that ship with Java 8. So, for completeness, we briefly mention the legacy date and time support (which is based on java.util.Date).

In older versions of Java, java.time is not available. Instead, programmers rely upon the legacy and rudimentary support provided by java.util.Date. Historically, this was the only way to represent timestamps, and although named Date this class actually consisted of both a date and a time component—and this led to a lot of confusion for many programmers.

There are many problems with the legacy support provided by Date, for example:

• The Date class is incorrectly factored. It doesn’t actually refer to a date, and instead is more like a timestamp. It turns out that we need different representations for a date, versus a date and time, versus an instantaneous timestamp.

• Date is mutable. We can obtain a reference to a date, and then change when it refers to.

• The Date class doesn’t actually accept ISO-8601, the universal ISO date standard, as being as valid date.

• Date has a very large number of deprecated methods.

The current JDK uses two constructors for Date—the void constructor that is intended to be the “now constructor,” and a constructor that takes a number of milliseconds since epoch.