

Copyright © 2012 Dorling Kindersley (India) Pvt. Ltd
This book is sold subject to the condition that it shall not, by way of trade or otherwise, be lent, resold, hired out, or otherwise circulated without the publisher's prior written consent in any form of binding or cover other than that in which it is published and without a similar condition including this condition being imposed on the subsequent purchaser and without limiting the rights under copyright reserved above, no part of this publication may be reproduced, stored in or introduced into a retrieval system, or transmitted in any form or by any means (electronic, mechanical, photocopying, recording or otherwise), without the prior written permission of both the copyright owner and the publisher of this book.
ISBN 978-81-317-6452-7
First Impression
Published by Dorling Kindersley (India) Pvt. Ltd, licensees of Pearson Education in South Asia.
Head Office: 7th Floor, Knowledge Boulevard, A-8(A), Sector 62, Noida 201 309, UP, India.
Registered Office: 11 Community Centre, Panchsheel Park, New Delhi 110 017, India.
Compositor: Cameo Corporate Services Ltd., Chennai.
Printer: xxx.
Today, the Internet has undoubtedly become the largest public data network that facilitates personal and business communications worldwide. The amount of traffic moving through the Internet as well as corporate networks is growing day by day. More and more people are communicating via e-mails, branch offices are using the Internet to remotely connect to their corporate networks and most commercial transactions such as shopping, bill payments and banking are also being done through the networks. Due to growing dependency of users, businesses and organizations on computer networks, it has become important to protect the information being exchanged from various security attacks. In addition, the confidentiality, authenticity and integrity of the messages moving across the networks must be ensured. This is where network security is important.
Network security is a set of protocols that facilitates the use of networks without any fear of security attacks. The most common and traditional technique used for providing network security is cryptography, which is a process of transforming messages into an unintelligible form before transmitting and converting them back to the original when received by the receiver. However, with the evolution of cryptography and network security disciplines, more practical and readily available applications such as Kerberos, Pretty Good Privacy (PGP), IPSec, Secure Socket Layer (SSL), Transport Layer Security (TLS) and firewalls have developed to implement the network security. Keeping in mind the importance of network security, almost all universities have integrated the study of cryptography and network security in B.Tech. (CSE and IT), MCA and MBA courses. The book in your hands, Cryptography and Network Security, in its unique easy-to-understand question-and-answer format directly addresses the need of students enrolled in these courses.
The book comprises questions and their corresponding answers on the basic issues to be addressed by cryptography and network security capability as well as practical applications that are being used for providing network security. The text has been designed to make it particularly easy for students to understand the principles and practice of cryptography and network security. An attempt has been made to make the book self-contained so that students can learn the subject by themselves. The organized and accessible format allows students to quickly find questions on specific topics.
The book Cryptography and Network Security is a part of series named Pearson Instant Learning Series (PILS), which has a number of books designed as quick reference guides.
Unique Features
1. Designed as a student friendly self-learning guide, the book is written in a clear, concise and lucid manner.
2. Easy-to-understand question-and-answer format.
3. Includes previously asked as well as new questions organized in chapters.
4. All types of questions including multiple-choice questions, short and long questions are covered.
5. Solutions to numerical questions asked at examinations are provided.
6. All ideas and concepts are presented with clear examples.
7. Text is well structured and well supported with suitable diagrams.
8. Inter-chapter dependencies are kept to a minimum.
9. A comprehensive index at the end of the book for quick access to desired topics.
Chapter Organization
All the questions-answers are organized into ten chapters. A brief description of these chapters is as follows:
 Chapter 1 provides an overview of basic concepts of network security. It discusses the need, goals and principles of network security as well as different kinds of attacks on computer systems and network. It also gives a brief idea of security services and security mechanisms.
Chapter 1 provides an overview of basic concepts of network security. It discusses the need, goals and principles of network security as well as different kinds of attacks on computer systems and network. It also gives a brief idea of security services and security mechanisms.
 Chapter 2 introduces the concept of cryptography, which is the most common technique used for providing network security. It describes important mathematical principles that are central to the design of ciphers. The chapter further discusses modular arithmetic, which is the fundamental concept to understand the working of ciphers. It also discusses the concept of cryptanalysis and various cryptanalysis attacks.
Chapter 2 introduces the concept of cryptography, which is the most common technique used for providing network security. It describes important mathematical principles that are central to the design of ciphers. The chapter further discusses modular arithmetic, which is the fundamental concept to understand the working of ciphers. It also discusses the concept of cryptanalysis and various cryptanalysis attacks.
 Chapter 3 deals with symmetric-key ciphers. It starts with a discussion on traditional symmetric-key ciphers that include various substitution ciphers such as additive, shift, multiplicative, affine, autokey, Playfair, Vigenere and Hill cipher and transposition ciphers. Then, the discussion moves on to two important categories of ciphers, namely stream and block ciphers. The chapter also includes a brief discussion on Shannon's theory of diffusion and confusion. Finally, the chapter concludes with a discussion on product ciphers proposed by Shannon, and the two categories of product ciphers, namely Feistel and non-Feistel ciphers.
Chapter 3 deals with symmetric-key ciphers. It starts with a discussion on traditional symmetric-key ciphers that include various substitution ciphers such as additive, shift, multiplicative, affine, autokey, Playfair, Vigenere and Hill cipher and transposition ciphers. Then, the discussion moves on to two important categories of ciphers, namely stream and block ciphers. The chapter also includes a brief discussion on Shannon's theory of diffusion and confusion. Finally, the chapter concludes with a discussion on product ciphers proposed by Shannon, and the two categories of product ciphers, namely Feistel and non-Feistel ciphers.
 Chapter 4 concentrates on the symmetric-key algorithms, which include Data Encryption Standard (DES) and Advanced Encryption Standard (AES). The chapter presents a detailed study on the design and analysis of DES. It also explains the general structure and the key expansion algorithm of AES.
Chapter 4 concentrates on the symmetric-key algorithms, which include Data Encryption Standard (DES) and Advanced Encryption Standard (AES). The chapter presents a detailed study on the design and analysis of DES. It also explains the general structure and the key expansion algorithm of AES.
 Chapter 5 is based on the number theory, which provides a mathematical background required to understand the asymmetric-key cryptography. It covers several important concepts related to prime numbers such as Fermat's theorem, Euler's totient function, Euler's theorem, Miller-Rabin algorithm and Chinese Remainder theorem.
Chapter 5 is based on the number theory, which provides a mathematical background required to understand the asymmetric-key cryptography. It covers several important concepts related to prime numbers such as Fermat's theorem, Euler's totient function, Euler's theorem, Miller-Rabin algorithm and Chinese Remainder theorem.
 Chapter 6 deals with asymmetric-key algorithms, which include RSA, Diffie-Hellman algorithm, ElGamal encryption system and Elliptic curve cryptography (ECC).
Chapter 6 deals with asymmetric-key algorithms, which include RSA, Diffie-Hellman algorithm, ElGamal encryption system and Elliptic curve cryptography (ECC).
 Chapter 7 focuses on message authentication mechanisms used to ensure that the integrity of the received message has been preserved. It explains various authentication functions and message authentication code (MAC). It also gives a detailed description of standard hash functions such as MD5, SHA-1 and Whirlpool. The chapter also spells out the concept of birthday attacks against hash functions.
Chapter 7 focuses on message authentication mechanisms used to ensure that the integrity of the received message has been preserved. It explains various authentication functions and message authentication code (MAC). It also gives a detailed description of standard hash functions such as MD5, SHA-1 and Whirlpool. The chapter also spells out the concept of birthday attacks against hash functions.
 Chapter 8 familiarizes the reader with the concept of digital signatures, and presents the essential properties and requirements of digital signatures, possible attacks on digital signatures and various digital signature schemes including RSA, ElGamal and DSS. The chapter then shifts its focus on authentication protocol and discusses its two categories, namely mutual authentication and one-way authentication.
Chapter 8 familiarizes the reader with the concept of digital signatures, and presents the essential properties and requirements of digital signatures, possible attacks on digital signatures and various digital signature schemes including RSA, ElGamal and DSS. The chapter then shifts its focus on authentication protocol and discusses its two categories, namely mutual authentication and one-way authentication.
 Chapter 9 presents the working principle of Kerberos protocol, X.509 authentication service and its certificates. The chapter also describes the security at the application layer covering PGP and S/MIME, security at the transport layer covering SSL and TSL, and security at the network layer describing IPSec.
Chapter 9 presents the working principle of Kerberos protocol, X.509 authentication service and its certificates. The chapter also describes the security at the application layer covering PGP and S/MIME, security at the transport layer covering SSL and TSL, and security at the network layer describing IPSec.
 Chapter 10 provides a description on system security, covering the concepts of intrusion prevention and detection, Honeypots, malicious software, viruses, digital immune system, behaviour-blocking software, firewalls and trusted systems.
Chapter 10 provides a description on system security, covering the concepts of intrusion prevention and detection, Honeypots, malicious software, viruses, digital immune system, behaviour-blocking software, firewalls and trusted systems.
Acknowledgements
 Our publisher Pearson Education, their editorial team and panel reviewers for their valuable contributions toward content enrichment.
Our publisher Pearson Education, their editorial team and panel reviewers for their valuable contributions toward content enrichment.
 Our technical and editorial consultants for devoting their precious time to improve the quality of the book.
Our technical and editorial consultants for devoting their precious time to improve the quality of the book.
 Our entire research and development team who have put in their sincere efforts to bring out a high-quality book.
Our entire research and development team who have put in their sincere efforts to bring out a high-quality book.
Feedback
For any suggestions and comments about this book, please feel free to send an e-mail to itlesl@rediffmail.com.
Hope you enjoy reading this book as much as we have enjoyed writing it.
ROHIT KHURANA
Founder and CEO
ITL ESL
1. What is the need for network security? Explain its goals.
Ans.: During the last two decades, computer networks have revolutionized the use of information. Information is now distributed over the network. Authorized users can use computer networks for sending and receiving information from a distance. People can also perform various tasks such as shopping, bill payments and banking over a computer network. This implies that the computer networks are nowadays used for carrying personal as well as financial data. Thus, it becomes important to secure the network, so that unauthorized people cannot access such sensitive information.
For secure communication, there are some basic goals of network security that should be achieved. These are as follows:
 Confidentiality: This refers to maintaining the secrecy of the message being transmitted over a network. Only the sender and the intended receiver should be able to understand and read the message, and eavesdroppers should not be able to read or modify the contents of the message. To achieve confidentiality the message should be transmitted over the network in an encrypted form.
Confidentiality: This refers to maintaining the secrecy of the message being transmitted over a network. Only the sender and the intended receiver should be able to understand and read the message, and eavesdroppers should not be able to read or modify the contents of the message. To achieve confidentiality the message should be transmitted over the network in an encrypted form.
 Integrity: Any message sent over the network must reach the intended receiver without any modification made to it. If any changes are made, the receiver must be able to detect that some alteration has happened. Integrity can be achieved by attaching a checksum to the message. This checksum ensures that an attacker cannot alter the message and, hence, that integrity is preserved.
Integrity: Any message sent over the network must reach the intended receiver without any modification made to it. If any changes are made, the receiver must be able to detect that some alteration has happened. Integrity can be achieved by attaching a checksum to the message. This checksum ensures that an attacker cannot alter the message and, hence, that integrity is preserved.
 Availability: Information created and stored by an organization should be available all the time to authorized users, failing which the information ceases to be useful. Availability is also equally important for organizations, because unavailability of information can adversely affect an organization's day-to-day operations. For example, imagine the status/service of a bank if its customers are unable to make transactions using their accounts.
Availability: Information created and stored by an organization should be available all the time to authorized users, failing which the information ceases to be useful. Availability is also equally important for organizations, because unavailability of information can adversely affect an organization's day-to-day operations. For example, imagine the status/service of a bank if its customers are unable to make transactions using their accounts.
2. What are the principles of network security?
Ans.: The principles of network security include confidentiality, integrity, availability, nonrepudiation, access control and authentication.
 Confidentiality: Refer previous question.
Confidentiality: Refer previous question.
 Integrity: Refer previous question.
Integrity: Refer previous question.
 Availability: Refer previous question.
Availability: Refer previous question.
 Nonrepudiation: After a message has been sent and received, the sender and receiver should not be able to deny about the sending and receiving of the message, respectively. The receiver should be able to prove that the message has come from the intended sender and not from anyone else. In addition, the receiver should be able to prove that the received message's contents are the same as sent by the sender.
Nonrepudiation: After a message has been sent and received, the sender and receiver should not be able to deny about the sending and receiving of the message, respectively. The receiver should be able to prove that the message has come from the intended sender and not from anyone else. In addition, the receiver should be able to prove that the received message's contents are the same as sent by the sender.
 Access control: The term ‘access’ involves writing, reading, executing and modifying. Thus, access control determines and controls who can access what. It regulates which user has access to a resource, under what circumstances the access is possible and which operations the user can perform on that resource. For example, we can specify that user
Access control: The term ‘access’ involves writing, reading, executing and modifying. Thus, access control determines and controls who can access what. It regulates which user has access to a resource, under what circumstances the access is possible and which operations the user can perform on that resource. For example, we can specify that user A is allowed to only view the records in a database but not to modify them. However, user B is allowed to read as well as update the records.
 Authentication: Authentication is concerned with determining whom you are communicating with. Authentication is necessary to ensure that the receiver has received the message from the actual sender, and not from an attacker. That is, the receiver should be able to authenticate the sender, which can be achieved by sharing a common secret code word, by sending digital signatures or by the use of digital certificates.
Authentication: Authentication is concerned with determining whom you are communicating with. Authentication is necessary to ensure that the receiver has received the message from the actual sender, and not from an attacker. That is, the receiver should be able to authenticate the sender, which can be achieved by sharing a common secret code word, by sending digital signatures or by the use of digital certificates.
3. Define a network security attack?
Ans.: A network security attack refers to an act of breaching the security or authentication routines of a network. Such an act is a threat to the basic goals of secure communication, such as confidentiality, integrity and authentication.
4. Explain passive attacks and active attacks.
Ans.: Network security attacks can be classified into two categories—passive attacks and active attacks.
Passive Attacks
In a passive attack, the attacker indulges in eavesdropping, that is, listening to a communication channel and monitoring the contents of a message. The term ‘passive’ indicates that the main goal of the intruder is just to gather information and not to do any alteration to the message or harm the system resources. A passive attack is hard to recognize, as the message is not tampered with or altered; therefore, the sender and receiver remains unaware that the message contents have been read by another party. However, some measures such as encryption are available to prevent such attacks.
Two types of passive attacks are:
 Release of message contents: This type of passive attack involves (1) capturing the sensitive information that is sent via email or (2) tapping a conversation that is conducted over a telephone line.
Release of message contents: This type of passive attack involves (1) capturing the sensitive information that is sent via email or (2) tapping a conversation that is conducted over a telephone line.
 Traffic analysis: In this type of attack, an intruder observes the frequency and length of messages being exchanged between communicating nodes. A passive attacker can then use this information for guessing the nature of the communication that was taking place.
Traffic analysis: In this type of attack, an intruder observes the frequency and length of messages being exchanged between communicating nodes. A passive attacker can then use this information for guessing the nature of the communication that was taking place.
Active Attacks
In an active attack, an intruder either alters the original message or creates a fake message. This attack tries to affect the operation of system resources. When compared to passive attacks, it is easier to recognize an active attack, but harder to prevent it. Active attacks can be classified into four categories, as follows:
 Masquerade: In computer terms, ‘masquerading’ is said to happen when an entity impersonates another. In such an attack, an unauthorized entity tries to gain more privileges than it is authorized for. Masquerading is generally done by using stolen IDs and passwords, or through bypassing authentication mechanisms.
Masquerade: In computer terms, ‘masquerading’ is said to happen when an entity impersonates another. In such an attack, an unauthorized entity tries to gain more privileges than it is authorized for. Masquerading is generally done by using stolen IDs and passwords, or through bypassing authentication mechanisms.
 Replay: This active attack involves capturing a copy of the message sent by the original sender and retransmitting it later to bring about an unauthorized result.
Replay: This active attack involves capturing a copy of the message sent by the original sender and retransmitting it later to bring about an unauthorized result.
 Modification of messages: This attack involves making certain modifications to the captured message, or delaying or reordering the messages to cause an unauthorized effect.
Modification of messages: This attack involves making certain modifications to the captured message, or delaying or reordering the messages to cause an unauthorized effect.
 Denial of service (DoS): This attack prevents the normal functioning or proper management of communication facilities. For example, a network server can be overloaded by unwanted packets, thus resulting in performance degradation. DoS attacks can interrupt and slow down the services of a network, or even completely jam a network.
Denial of service (DoS): This attack prevents the normal functioning or proper management of communication facilities. For example, a network server can be overloaded by unwanted packets, thus resulting in performance degradation. DoS attacks can interrupt and slow down the services of a network, or even completely jam a network.
5. Explain various network security services.
Ans.: The International Telecommunication Union-Telecommunication Standardization Sector (ITU-T), also known as X.800, defines security service as ‘a service provided by a protocol layer of communicating open system, which ensures adequate security of the systems or of data transfers’. Another definition of security service is found in RFC 2828, which defines it as ‘a processing or communication service that is provided by a system to give a specific kind of protection to system resources; security services implement security policies and are implemented by security mechanisms’. According to X.800, security services are divided into five categories and 14 specific services (see Figure 1.1).
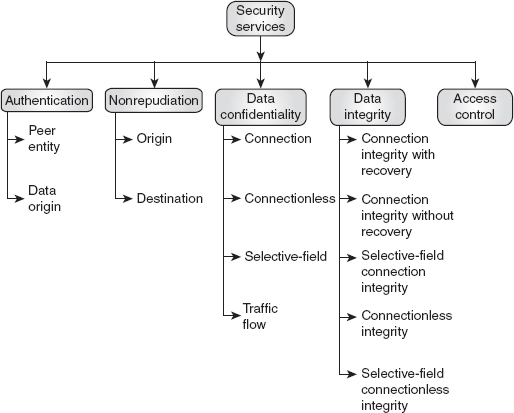
Figure 1.1 Security Services
 Authentication: This service provides the assurance that the communicating party at the other end of the line is the correct party. Two types of authentication services defined by X.800 are:
Authentication: This service provides the assurance that the communicating party at the other end of the line is the correct party. Two types of authentication services defined by X.800 are:
 Peer entity authentication: This provides authentication of the receiver or sender during the connection establishment phase in connection-oriented communication.
Peer entity authentication: This provides authentication of the receiver or sender during the connection establishment phase in connection-oriented communication.
 Data origin authentication: This service provides authentication of the data source in a connectionless communication.
Data origin authentication: This service provides authentication of the data source in a connectionless communication.
 Nonrepudiation: This service provides the assurance that the sender and receiver are not able to deny about the sending and receiving of the message, respectively. X.800 defines two types of services for nonrepudiation:
Nonrepudiation: This service provides the assurance that the sender and receiver are not able to deny about the sending and receiving of the message, respectively. X.800 defines two types of services for nonrepudiation:
 Origin nonrepudiation: This helps the receiver prove that the message was sent by the intended sender.
Origin nonrepudiation: This helps the receiver prove that the message was sent by the intended sender.
 Destination nonrepudiation: This helps the sender prove that the message was delivered to the intended receiver.
Destination nonrepudiation: This helps the sender prove that the message was delivered to the intended receiver.
 Data confidentiality: This service provides protection against the disclosure of data to unauthorized parties. For data confidentiality, X.800 defines four types of services:
Data confidentiality: This service provides protection against the disclosure of data to unauthorized parties. For data confidentiality, X.800 defines four types of services:
 Connection confidentiality: This provides confidentiality for all the messages transmitted between two users on a connection-oriented transmission, such as over a TCP connection.
Connection confidentiality: This provides confidentiality for all the messages transmitted between two users on a connection-oriented transmission, such as over a TCP connection.
 Connectionless confidentiality: This service provides confidentiality for all user data in a single data block.
Connectionless confidentiality: This service provides confidentiality for all user data in a single data block.
 Selective-field confidentiality: This provides confidentiality for a single message or some selected data fields of a message in a single data block or on a connection.
Selective-field confidentiality: This provides confidentiality for a single message or some selected data fields of a message in a single data block or on a connection.
 Traffic flow confidentiality: This provides confidentiality for the data derived from the traffic flow analysis.
Traffic flow confidentiality: This provides confidentiality for the data derived from the traffic flow analysis.
 Data integrity: This service provides assurance that data received by the receiver are exactly the same (with no modification, duplication, reordering, deletion or insertion) as sent by the authorized sender. For data integrity, the services defined by X.800 are as follows:
Data integrity: This service provides assurance that data received by the receiver are exactly the same (with no modification, duplication, reordering, deletion or insertion) as sent by the authorized sender. For data integrity, the services defined by X.800 are as follows:
 Connection integrity with recovery: This provides integrity to the entire user data or stream of messages on a connection. That is, it detects any modification, duplication, reordering, deletion, insertion or replay made to data or messages within an entire data or message sequence. If any change in data is detected, then this service tries to recover the original data.
Connection integrity with recovery: This provides integrity to the entire user data or stream of messages on a connection. That is, it detects any modification, duplication, reordering, deletion, insertion or replay made to data or messages within an entire data or message sequence. If any change in data is detected, then this service tries to recover the original data.
 Connection integrity without recovery: This service provides integrity to the entire user data or stream of messages on a connection. That is, it detects any change made to the messages or data, but does not try to recover the original data.
Connection integrity without recovery: This service provides integrity to the entire user data or stream of messages on a connection. That is, it detects any change made to the messages or data, but does not try to recover the original data.
 Selective-field connection integrity: This provides integrity to selected data fields within a block of user data or selected part of the message over a connection.
Selective-field connection integrity: This provides integrity to selected data fields within a block of user data or selected part of the message over a connection.
 Connectionless integrity: This provides integrity to a single data block or a single message in a connectionless communication and detects any modification made to data. It may also provide detection of replay attacks.
Connectionless integrity: This provides integrity to a single data block or a single message in a connectionless communication and detects any modification made to data. It may also provide detection of replay attacks.
 Selective-field connectionless integrity: This provides integrity of selected data fields within a block of user data in a connectionless communication and also detects any modification in these fields.
Selective-field connectionless integrity: This provides integrity of selected data fields within a block of user data in a connectionless communication and also detects any modification in these fields.
 Access control: This provides protection to data and resources from unauthorized access. This service defines the condition for accessing any data and controls the users who can access the resources.
Access control: This provides protection to data and resources from unauthorized access. This service defines the condition for accessing any data and controls the users who can access the resources.
6. Explain various security mechanisms. How are they related to security services?
Ans.: Security mechanisms have been defined by ITU-T (X.800). They are used to implement OSI security services and are incorporated into the suitable protocol layer. Some of the security mechanisms recommended by ITU-T (X.800) are shown in Figure 1.2.
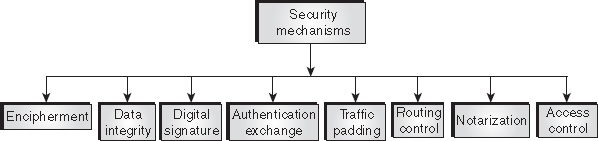
Figure 1.2 Security Mechanisms
 Encipherment: This refers to the transformation of the message or data with the help of mathematical algorithms. The main aim of this mechanism is to provide confidentiality. The two techniques that are used for encipherment are cryptography and steganography.
Encipherment: This refers to the transformation of the message or data with the help of mathematical algorithms. The main aim of this mechanism is to provide confidentiality. The two techniques that are used for encipherment are cryptography and steganography.
 Data integrity: This refers to the method of ensuring the integrity of data. For this, the sender computes a check value by applying some process over the data being sent, and then appends this value to the data. On receiving the data, the receiver again computes the check value by applying the same process over the received data. If the newly computed check value is same as the received one, then it means that the integrity of data is preserved.
Data integrity: This refers to the method of ensuring the integrity of data. For this, the sender computes a check value by applying some process over the data being sent, and then appends this value to the data. On receiving the data, the receiver again computes the check value by applying the same process over the received data. If the newly computed check value is same as the received one, then it means that the integrity of data is preserved.
 Digital signature: This refers to the method of electronic signing of data by the sender and electronic verification of the signature by the receiver. It provides information about the author, date and time of the signature, so that the receiver can prove the sender's identity.
Digital signature: This refers to the method of electronic signing of data by the sender and electronic verification of the signature by the receiver. It provides information about the author, date and time of the signature, so that the receiver can prove the sender's identity.
 Authentication exchange: This refers to the exchange of some information between two communicating parties to prove their identity to each other.
Authentication exchange: This refers to the exchange of some information between two communicating parties to prove their identity to each other.
 Traffic padding: This refers to the insertion of extra bits into the stream of data traffic to prevent traffic analysis attempts by attackers.
Traffic padding: This refers to the insertion of extra bits into the stream of data traffic to prevent traffic analysis attempts by attackers.
 Routing control: This refers to the selection of a physically secured route for data transfer. It also allows changing of route if there is any possibility of eavesdropping on a certain route.
Routing control: This refers to the selection of a physically secured route for data transfer. It also allows changing of route if there is any possibility of eavesdropping on a certain route.
 Notarization: This refers to the selection of a trusted third party for ensuring secure communication between two communicating parties.
Notarization: This refers to the selection of a trusted third party for ensuring secure communication between two communicating parties.
 Access control: It refers to the methods used to ensure that a user has the right to access the data or resource.
Access control: It refers to the methods used to ensure that a user has the right to access the data or resource.
Security services and mechanisms share a close relationship with each other. One or more security mechanisms are used together to provide a security service. In addition, the same mechanism can also be used in many security services. Table 1.1 lists the security services along with the mechanisms that are used in these services.
| Security services | Security mechanisms |
|---|---|
| Authentication | Encipherment, digital signature and authentication exchange |
| Nonrepudiation | Data integrity, digital signature and notarization |
| Data confidentiality | Encipherment and routing control |
| Data integrity | Encipherment, data integrity, and digital signature |
| Access control | Access control mechanism |
7. Briefly explain the model for network security.
Ans.: With the phenomenal increase in the use of computer networks such as the Internet over the last few years, it has become essential to enhance the security of the network. To provide secured communication over the network, a general model of network security was created, which enhanced network security. This model consists of various components, which are as follows:
 Message: This is the information that is to be transmitted over the network.
Message: This is the information that is to be transmitted over the network.
 Principals: These refer to communication nodes, one which transmits the message (sender) and the other receives it (receiver).
Principals: These refer to communication nodes, one which transmits the message (sender) and the other receives it (receiver).
 Security-related transformation: This refers to the transformations made to the information to be sent, so that it is unreadable to an intruder. An example for such transformation includes either encryption of the message or inserting a message to verify the identity of the sender.
Security-related transformation: This refers to the transformations made to the information to be sent, so that it is unreadable to an intruder. An example for such transformation includes either encryption of the message or inserting a message to verify the identity of the sender.
 Secret information: This refers to the information that is shared between the two principals and used while applying the transformation at both the sender's and receiver's ends. For example, in case of encryption, the secret information can be a key used for encrypting and decrypting the message.
Secret information: This refers to the information that is shared between the two principals and used while applying the transformation at both the sender's and receiver's ends. For example, in case of encryption, the secret information can be a key used for encrypting and decrypting the message.
 Secure message: This refers to the message obtained after applying a transformation. It contains the secret code that helps the receiver retrieve the original message.
Secure message: This refers to the message obtained after applying a transformation. It contains the secret code that helps the receiver retrieve the original message.
 Logical information channel: This refers to the transmission route from a source to a destination, connected via a network. The route is established by the supportive use of communicating protocols by both parties.
Logical information channel: This refers to the transmission route from a source to a destination, connected via a network. The route is established by the supportive use of communicating protocols by both parties.
 Trusted third party: This is an entity that may either be responsible for transmitting the secret information to the two trusted parties while protecting it from an attacker, or may be responsible for settling disputes regarding the authenticity of a message transmission between two parties.
Trusted third party: This is an entity that may either be responsible for transmitting the secret information to the two trusted parties while protecting it from an attacker, or may be responsible for settling disputes regarding the authenticity of a message transmission between two parties.
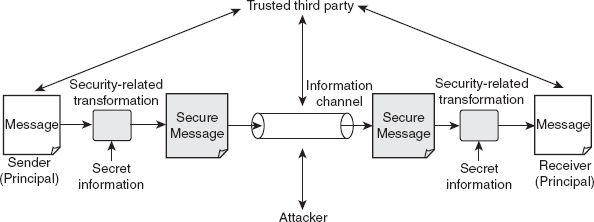
Figure 1.3 Model of Network Security
According to this model, there are four basic tasks that are required for designing any security service. These tasks are:
 Designing an algorithm to perform security-related transformation. The algorithm should be designed in such a way that an intruder cannot defeat its purpose.
Designing an algorithm to perform security-related transformation. The algorithm should be designed in such a way that an intruder cannot defeat its purpose.
 Generating the secret information to be used with the algorithm.
Generating the secret information to be used with the algorithm.
 Developing some techniques for the sharing and distribution of the secret information.
Developing some techniques for the sharing and distribution of the secret information.
 Selecting a protocol to be used by the two parties. This protocol makes use of the secret information and security algorithm to achieve a specific security service.
Selecting a protocol to be used by the two parties. This protocol makes use of the secret information and security algorithm to achieve a specific security service.
This model secures the information in such a way that an intruder on the network cannot access it. However, within the organization, the information's security can still be threatened by unauthorized access, or by software attacks such as viruses and worms. To protect information from such threats, some security mechanisms should be implemented, as follows:
 Password-based login: This is used to deny access to all unauthorized users.
Password-based login: This is used to deny access to all unauthorized users.
 Screening login: This is used to detect and remove viruses, worms and other similar attacks.
Screening login: This is used to detect and remove viruses, worms and other similar attacks.
8. Categorize different types of network security attacks on the basis of security goals.
Ans.: As we know, for secured communication, some goals such as confidentiality, integrity and availability have been defined. However, these goals can be threatened by various security attacks. The categorization of attacks on the basis of security goals is shown in Figure 1.4.
 Attacks to integrity: The attacks that threaten the integrity of the data are masquerading, modification, repudiation and replay.
Attacks to integrity: The attacks that threaten the integrity of the data are masquerading, modification, repudiation and replay.
 Masquerading: Refer Question 4 in this chapter.
Masquerading: Refer Question 4 in this chapter.
 Modification: Refer Question 4 in this chapter.
Modification: Refer Question 4 in this chapter.
 Repudiation: Repudiation occurs when the message sender denies that the message was sent by him/her, or when the message receiver denies that the message was received by him/her.
Repudiation: Repudiation occurs when the message sender denies that the message was sent by him/her, or when the message receiver denies that the message was received by him/her.
 Replay: Refer Question 4 in this chapter.
Replay: Refer Question 4 in this chapter.
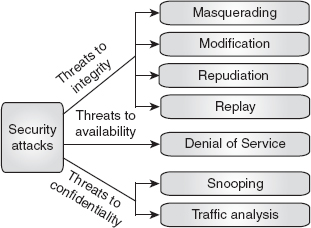
Figure 1.4 Categorization of Attacks in Relation to Security Goals
 Attacks to confidentiality: The attacks that threaten the confidentiality of data are snooping and traffic analysis.
Attacks to confidentiality: The attacks that threaten the confidentiality of data are snooping and traffic analysis.
 Snooping: Snooping refers to interception or unauthorized access of data. For example, an unauthorized entity may access a file containing confidential information during its transmission over a network and use that information for its benefits. Snooping can be prevented with the help of various encryption techniques, by making the data non-understandable to the unauthorized entity.
Snooping: Snooping refers to interception or unauthorized access of data. For example, an unauthorized entity may access a file containing confidential information during its transmission over a network and use that information for its benefits. Snooping can be prevented with the help of various encryption techniques, by making the data non-understandable to the unauthorized entity.
 Traffic analysis: Refer Question 4 in this chapter.
Traffic analysis: Refer Question 4 in this chapter.
 Attacks to availability: The attack that threatens availability is called denial of service (DoS).
Attacks to availability: The attack that threatens availability is called denial of service (DoS).
 Denial of service (DoS): Refer Question 4 in this chapter.
Denial of service (DoS): Refer Question 4 in this chapter.
Multiple-choice Questions
1. __________ ensures that a message was received by the receiver from the actual sender and not from an attacker.
(a) Authentication
(b) Authorization
(c) Integration
(d) None of these
2. Which of the following services is not an authentication service?
(a) Peer entity authentication
(b) Data origin authentication
(c) Data destination authentication
(d) None of these
3. Which of the following is a passive attack?
(a) Masquerade
(b) Replay
(c) Denial of service (DoS)
(d) Traffic analysis
4. Which of the following attacks is not a threat to the integrity of data?
(a) Masquerade
(b) Modification
(c) Repudiation
(d) Snooping
5. Which RFC document includes a definition of security service?
(a) RFC 2828
(b) RFC 2401
(c) RFC 3310
(d) RFC 6600
Answers
1. (a)
2. (c)
3. (d)
4. (d)
5. (a)
1. Explain the term cryptography in brief.
Ans.: Cryptography is a means for implementing some security mechanisms. The term cryptography is derived from the Greek word kryptos, which means “secret writing”. In simple terms, cryptography is the process of altering messages in a way that their meaning is hidden from adversaries who might intercept them. It allows the sender to disguise a message to prevent it from being read or altered by an intruder, and it also enables the receiver to recover the original message from the disguised one.
In data and telecommunications, cryptography is an essential technique required for communicating over any untrusted medium, which includes any network, such as the Internet. By using cryptographic techniques, the sender can first encrypt a message and then transmit it through the network. The receiver on the other hand can decrypt the message and recover its original contents.
Cryptography relies upon two basic components: an algorithm (or cryptographic methodology) and a key. Algorithms are the complex mathematical formulae and keys are the strings of bits. For two parties to communicate over a network (the Internet), they must use the same algorithm (or algorithms that are designed to work together). In some cases, they must also use the same key.
2. Define the following terms:
(a) Plaintext
(b) Ciphertext
(c) Encryption
(d) Decryption
(e) Cipher
(f) Key
Ans.: These terms can be defined as follows:
(a) Plaintext: It refers to the original unencrypted message that the sender wishes to send.
(b) Ciphertext: It refers to the encrypted message that is received by the receiver.
(c) Encryption: It is the process of encrypting the plaintext so that the ciphertext can be produced. Plaintext is transformed into ciphertext using the encryption algorithm.
(d) Decryption: It is the reverse of the encryption process. In this process, the ciphertext is converted back to the plaintext using a decryption algorithm.
(e) Ciphers: The encryption and decryption algorithms are together known as ciphers. Ciphers need not necessarily be unique for each communicating pair; rather a single cipher can be used for communication between multiple pairs of senders and receivers.
(f) Key: A key is usually a number or a set of numbers on which the cipher operates. Encryption and decryption algorithms make use of a key to encrypt or decrypt messages, respectively. At the sender's end, the encryption algorithm and encryption key are required to convert the plaintext into ciphertext. At the receiver's end, a decryption algorithm uses the decryption key to convert ciphertext back into the plaintext. The longer the key is, the harder it is for an attacker to decrypt the message.
3. Explain symmetric-key and asymmetric-key encipherment.
Ans.: Traditionally, cryptography involves the use of the same key for encrypting or decrypting the messages (symmetric-key encipherment). However, modern cryptography involves the use of different keys for encryption and decryption (asymmetric-key encipherment).
Symmetric-key Encipherment
The symmetric-key encipherment, sometimes also called secret-key encipherment or secret-key cryptography, uses a single shared key (secret key) for both encryption and decryption of data. Thus, it is obvious that the key must be known to both the sender and the receiver. As shown in Figure 2.1, the sender uses the shared key and the encryption algorithm to transform the plaintext into ciphertext. The ciphertext is then sent to the receiver via a communication network. The receiver applies the same key and the decryption algorithm to decrypt the ciphertext and to recover the plaintext. Some examples of symmetric-key algorithms include Data Encryption Standard (DES), double DES, triple DES, and Advanced Encryption Standard (AES).
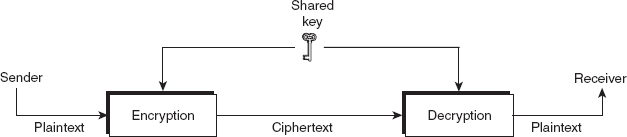
Figure 2.1 Message exchange using secret key
The main problem in secret-key cryptography is getting the sender and receiver to agree on the secret key without anyone else finding it out. If the key is compromised, the security offered by secret-key cryptography is severely reduced or eliminated. Secret-key cryptography assumes that the parties who share a key rely upon each other not to disclose the key and protect it against modification. If they are in separate physical locations, they must trust a medium such as the courier or a phone system to prevent the disclosure of the secret key. Anyone who overhears or intercepts the key in transit can later read, modify, and forge all messages encrypted or authenticated using that key.
Asymmetric-key Encipherment
The asymmetric-key encipherment, sometimes also called public-key encipherment or public-key cryptography, was introduced by Diffie and Hellman in 1976 to overcome the problem found in symmetric-key cryptography. It involves the use of two different keys for encryption and decryption. These two keys are referred to as the public key (used for encryption) and the private key (used for decryption). Each authorized user has a pair of public and private keys. The public key of each user is known to everyone, whereas the private key is known to its owner only.
Now, suppose that a user A wants to transfer some information to user B securely. The user A encrypts the data by using the public key of B and sends the encrypted message to B. On receiving the encrypted message, B decrypts it by using his/her private key. Since decryption process requires a private key of user B, which is only known to B, the information is transferred securely. Figure 2.2 illustrates the whole process. RSA is a well-known example of asymmetric-key algorithm.
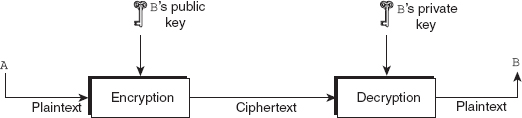
Figure 2.2 Message exchange using public key
The main advantage of public-key cryptography is that the need for the sender and the receiver to share the secret key is eliminated and all communication involves only public keys. Thus, the private key is never transmitted or shared. Anyone can send a confidential message using a public key, but the message can only be decrypted with a private key, which is in the sole possession of the intended recipient.
4. Differentiate between symmetric-key and asymmetric-key cryptography.
Ans.: Some differences between symmetric-key and asymmetric-key cryptography are listed in Table 2.1.
| Symmetric-key cryptography | Asymmetric-key cryptography |
|---|---|
| 1. It uses a single key for both encryption and decryption of data. | 1. It uses two different keys—public key for encryption and private key for decryption. |
| 2. Both the communicating parties share the same algorithm and the key. | 2. Both the communicating parties should have at least one of the matched pair of keys. |
| 3. The processes of encryption and decryption are very fast. | 3. The encryption and decryption processes are slower as compared to symmetric-key cryptography. |
| 4. Key distribution is a big problem. | 4. Key distribution is not a problem. |
| 5. The size of encrypted text is usually same or less than the original text. | 5. The size of encrypted text is usually more than the size of the original text. |
| 6. It can only be used for confidentiality, that is, only for encryption and decryption of data. | 6. It can be used for confidentiality of data as well as for integrity and non-repudiation checks (that is, for digital signatures). |
| 7. DES and AES are the commonly used symmetric-key algorithms. | 7. The most commonly used asymmetric-key algorithm is RSA. |
5. What is cryptanalysis? Also, discuss different cryptanalysis attacks.
Ans.: Cryptanalysis is the art and science of breaking the encrypted codes that are created by applying some cryptographic algorithms. The person who performs cryptanalysis is known as a cryptanalyst. A cryptanalysis attack is made by a cryptanalyst to obtain the plaintext or the key that was used to encrypt a message. Depending on the information that the cryptanalyst has, cryptanalysis attacks can be classified under the following categories:
 Ciphertext-only attack: In this type of attack, the cryptanalyst has a part of the ciphertext available and using this information, he/she tries to find out the corresponding key and decipher the plaintext. This attack is based on the assumption that the cryptanalyst knows the algorithm that has been used to encrypt the message and can easily intercept the ciphertext. These types of attacks are very common because the attacker just needs to have the knowledge of the ciphertext. However, we can prevent a cryptanalyst from decrypting the ciphertext by using a strong cipher, which makes it very difficult for the cryptanalyst to decrypt the message. Some common methods that can be used to determine the key or break the ciphers in ciphertext-only attacks include brute-force, statistical, and pattern attacks. Figure 2.3 depicts the process of ciphertext-only attack where
Ciphertext-only attack: In this type of attack, the cryptanalyst has a part of the ciphertext available and using this information, he/she tries to find out the corresponding key and decipher the plaintext. This attack is based on the assumption that the cryptanalyst knows the algorithm that has been used to encrypt the message and can easily intercept the ciphertext. These types of attacks are very common because the attacker just needs to have the knowledge of the ciphertext. However, we can prevent a cryptanalyst from decrypting the ciphertext by using a strong cipher, which makes it very difficult for the cryptanalyst to decrypt the message. Some common methods that can be used to determine the key or break the ciphers in ciphertext-only attacks include brute-force, statistical, and pattern attacks. Figure 2.3 depicts the process of ciphertext-only attack where A and B are the communicating parties and C is the cryptanalyst (attacker).
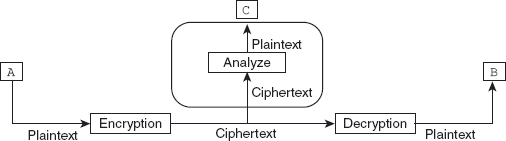
Figure 2.3 Ciphertext-only attack
 Known-plaintext attack: In this type of attack, the attacker already has some plaintext-ciphertext pairs in addition to the ciphertext that he/she wishes to break. Figure 2.4 depicts the process of known-plaintext attack by
Known-plaintext attack: In this type of attack, the attacker already has some plaintext-ciphertext pairs in addition to the ciphertext that he/she wishes to break. Figure 2.4 depicts the process of known-plaintext attack by C during communication between A and B. Suppose that A sent a secret message to B; however, later, A made the contents of that message public. Further, assume that the attacker C has kept both ciphertext and plaintext (which is now public). Thus, C tries to obtain a relationship between these pairs to find the key used to encrypt the plaintext so that he/she can break the next block of ciphertext from A to B; provided that A uses the same key to encrypt the message as that for the previous message. This type of attack is easy to implement because the attacker has more information to analyze the ciphertext. However, this attack happens rarely because it is more likely that the sender changes the key for every transmission of message, or that the message contents are not made public.
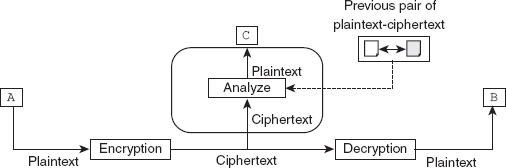
Figure 2.4 Known-plaintext attack
 Chosen-plaintext attack: This attack is similar to the known-plaintext attack with the only difference being that in this attack, the attacker
Chosen-plaintext attack: This attack is similar to the known-plaintext attack with the only difference being that in this attack, the attacker C himself/herself chooses the plaintext–ciphertext pairs. However, it is possible only if C gets access to A's computer by some means. The attacker C can then select some plaintext from A's computer that helps him/her to intercept the created ciphertext. This process is shown in Figure 2.5.
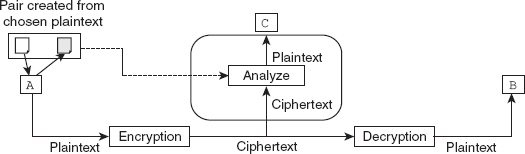
Figure 2.5 Chosen-plaintext attack
 Chosen-ciphertext attack: A chosen-ciphertext attack is similar to a chosen-plaintext attack. The only difference between the two being that in chosen-ciphertext attack, the attacker
Chosen-ciphertext attack: A chosen-ciphertext attack is similar to a chosen-plaintext attack. The only difference between the two being that in chosen-ciphertext attack, the attacker C chooses some ciphertext and then decrypts it to make a ciphertext-plaintext pair. This is possible if C gets access to B's computer. This process is shown in Figure 2.6.
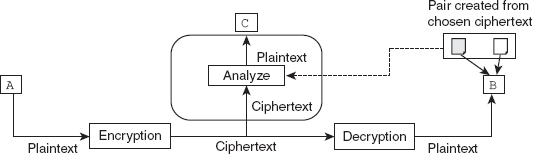
Figure 2.6 Chosen-ciphertext attack
 Chosen-text attack: A chosen-text attack is a combination of chosen-plaintext and chosen-ciphertext attack.
Chosen-text attack: A chosen-text attack is a combination of chosen-plaintext and chosen-ciphertext attack.
6. What is key management? Also, explain the functions of key management.
Ans.: Though cryptography enables maintaining the secrecy of a message, it works only as long as the keys used for encryption and decryption are kept secret. Thus, the secrecy of cryptographic keys is central to the encryption mechanism, and it is achieved through key management. Key management refers to the collection of processes used for the generation, storage, installation, transcription, recording, change, disposition, and control of keys that are used in cryptography. It is essential to the secure ongoing operation of any cryptosystem. The various functions of key management are as follows:
 Generation: This process involves the selection of a key that is to be used for encrypting and decrypting the messages. The key may be generated for the sender, receiver, or an application. It must be long enough to be predicted by a cryptanalyst. Moreover, it must be chosen randomly and its information must not be leaked during the whole process.
Generation: This process involves the selection of a key that is to be used for encrypting and decrypting the messages. The key may be generated for the sender, receiver, or an application. It must be long enough to be predicted by a cryptanalyst. Moreover, it must be chosen randomly and its information must not be leaked during the whole process.
 Distribution: This process involves all the efforts made in carrying the key from the point where it is generated to the point where it is to be used. Distribution is more difficult in symmetric-key cryptography where the key has to be transmitted via a secure channel.
Distribution: This process involves all the efforts made in carrying the key from the point where it is generated to the point where it is to be used. Distribution is more difficult in symmetric-key cryptography where the key has to be transmitted via a secure channel.
 Installation: This process involves getting the key into the storage of the device or the process that needs to use this key. Note that if this process involves manual operations, then it might result in leakage of key information.
Installation: This process involves getting the key into the storage of the device or the process that needs to use this key. Note that if this process involves manual operations, then it might result in leakage of key information.
 Storage: This process involves maintaining the confidentiality of stored or installed keys while preserving the integrity of the storage mechanism. The mechanism may be designed in such a way that once the key is installed, no one from the outside the encryption machine can intercept it. Alternatively, for an effective implementation, the key may be stored in an encrypted form such that the knowledge of the stored key does not disclose the behaviour of the device in which the key is being used.
Storage: This process involves maintaining the confidentiality of stored or installed keys while preserving the integrity of the storage mechanism. The mechanism may be designed in such a way that once the key is installed, no one from the outside the encryption machine can intercept it. Alternatively, for an effective implementation, the key may be stored in an encrypted form such that the knowledge of the stored key does not disclose the behaviour of the device in which the key is being used.
 Change: This process involves ending with the use of one key and starting the use of another. The longer the key is in use and more is the traffic encrypted by it, higher are the chances that it will be intercepted. Therefore, the key must be changed after some time. It may noted that the information about the key is prone to leakage during the key change time.
Change: This process involves ending with the use of one key and starting the use of another. The longer the key is in use and more is the traffic encrypted by it, higher are the chances that it will be intercepted. Therefore, the key must be changed after some time. It may noted that the information about the key is prone to leakage during the key change time.
7. Describe the general rules for maintaining an effective key management system?
Ans.: An effective key management system should follow certain basic rules that are defi ned as follows:
 The secret key must be stored and transmitted in a secure manner because disclosure of the secret key makes the data unsecured.
The secret key must be stored and transmitted in a secure manner because disclosure of the secret key makes the data unsecured.
 The longer the same key is in use, the easier it becomes to crack the key. Thus, the key must be changed from time to time.
The longer the same key is in use, the easier it becomes to crack the key. Thus, the key must be changed from time to time.
 The key must be generated randomly, so that it is hard for any attacker to guess it. The higher the randomness of the key is, higher will be the quality of the key, making it progressively more difficult to guess it.
The key must be generated randomly, so that it is hard for any attacker to guess it. The higher the randomness of the key is, higher will be the quality of the key, making it progressively more difficult to guess it.
 If the length of the key is short, its lifetime must also be short. That is, a short key must not be used for a longer period of time.
If the length of the key is short, its lifetime must also be short. That is, a short key must not be used for a longer period of time.
 The key must be destroyed properly after its use.
The key must be destroyed properly after its use.
8. Briefly discuss the concept of steganography.
Ans.: Steganography, like cryptography, is a technique to implement security mechanisms. The term steganography comes from the Greek word steganos, which means “concealed writing”. Steganography is the technique of writing a message in such a way that apart from the sender and the receiver, no one will suspect the existence of the message. It enables the sender to hide a message inside another message. Although both steganography and cryptography are security mechanisms intended to protect the messages from attackers, but still they differ from each other. Where cryptography conceals the contents of a message by enciphering, steganography conceals the message itself by covering it with something.
Some of the traditional techniques of steganography include:
 Marking selected letters of a printed document with a pencil such that the marks are visible only when the document is exposed at a specific angle to bright light.
Marking selected letters of a printed document with a pencil such that the marks are visible only when the document is exposed at a specific angle to bright light.
 Use of some invisible ink (such as onion juice, lemon juice, or some ammonia salt) to write a secret message such that the contents of a message are not visible until heated or some other chemical is applied.
Use of some invisible ink (such as onion juice, lemon juice, or some ammonia salt) to write a secret message such that the contents of a message are not visible until heated or some other chemical is applied.
 Use of microdots or pin punchers on selected letters such that these dots are not visible until the paper is exposed in front of a light.
Use of microdots or pin punchers on selected letters such that these dots are not visible until the paper is exposed in front of a light.
Some modern techniques of steganography include hiding of a secret message within an image, audio or video file by inserting secret binary message information during the digitization process. Although the digitization process may result in an extra overhead to hide a relatively small message, it is more effective when used along with cryptography.
9. Explain Euclidean algorithm for finding the greatest common divisor.
Ans.: The Euclidean algorithm (also called Euclid's algorithm) is an efficient algorithm for finding the greatest common divisor (GCD) of two positive integers. This algorithm was invented by the Greek mathematician Euclid and is hence named after him. Given two positive integers x and y, then another positive number (say, a) is called the gcd of x and y if and only if the following conditions are satisfied:
(i) a divides both x and y.
(ii) Any other common divisor of x and y also divides a.
In other words, gcd(x,y)=a if a is the largest integer that divides both x and y.
Euclidean's algorithm computes the gcd of two positive integers, x and y, based on the following facts:
(i) gcd(x,0)=x, that is, if the second integer is zero, then the gcd is the first integer.
(ii) gcd(x,y)=gcd(y,r), where r is the remainder obtained on dividing x by y.
Algorithm
The following are the steps to find the gcd of two positive integers x and y, where x>y>0 using Euclidean's algorithm, are as follows:
1. a:=x
2. b:=y
3. while (b>0)
{
q:=a/b
r:=a-q*b
a:=b
b:=r
}
4. gcd(x,y):=a
In this algorithm, we have used two variables a and b to hold the remainders produced during the reduction process. To start with, variables a and b are initialized with x and y, respectively. During each step in the reduction process, we calculate the remainder of a divided by b and then store it into the variable r. Then, a and b are replaced with b and r, respectively. This process is continued until the value of b becomes zero. Eventually, we get the gcd(x, y)as a.
10. Write a short note on modular arithmetic.
Ans.: In mathematics, to perform a division operation, we need two inputs, a divisor (say, m) and a dividend (say, x). After performing the operation we get two outputs, a quotient (say, q) and a remainder (say, r). That is, the division relationship can be expressed as follows:
x=m*q+r
However, in modular arithmetic, we are interested in only one output, that is, the remainder, while the other output (that is, the quotient) is not considered. Thus, in this case, the division operation can be expressed as a binary operator having two inputs, the integers x and m and only one output r. This binary operator is referred to as the modulo operator (written as mod). The input m (divisor) to the modulo operator is referred to as the modulus, while the output r is referred to as the residue. Thus, we can say that:
x mod m=r
where x is an integer from the set of integers Z={…,-3,-2,-1,0,1,2,3,…} and the modulus (m) and residue (r) are the positive integers. In case the value of x is negative, the value of r also comes out negative. Thus, to make it non-negative, the modulus m is added to r.
11. Explain the following with reference to modular arithmetic:
(a) Set of residues
(b) Congruence
(c) Additive and multiplicative inverse
Ans.: (a) Set of residues: Consider a modulo operation x mod m=r, where x is an integer from a set of integers Z while m and r are positive integers. The result of this operation is always an integer less than m. That is, the value of r lies between 0 and m-1. Thus, it can be said that the modulo operation results in a set containing elements from 0 to m-1. In modular arithmetic, this set is called the set of least residues modulo m (denoted as Zm) or simply the set of residues. There can be infinite possible instances of Zm, one for each value of m. For example, Z11 can have 11 values {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, Z4 can have four values {0, 1, 2, 3}, and so on.
Modular arithmetic allows three binary operations: addition, subtraction, and multiplication to be applied on the elements of Zm. After applying each operation, the result obtained may need to be mapped to Zm with the help of the modulo operator. To understand, consider three elements x, y, and z such that both x and y belong to Z (or Zm) and z belongs to Zm. Then the binary operations in Zm can be expressed as (also see Figure 2.7):
(x+y) mod m=z
(x-y) mod m=z
(x*y) mod m=z
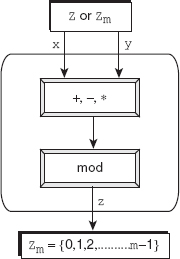
Figure 2.7 Binary operations in Zm
(b) Congruence: There is always a many-to-one relationship between Z and Zm. That is, many elements of the set Z can map to a single element of Zm. For example, modulo operations 3 mod 10, 13 mod 10, and 23 mod 10 result in the same value (equal to 3). Thus, these numbers (3, 13, and 23) are referred to as congruent mod 10 in modular arithmetic. To represent the congruence relationship between two integers, the congruence operator represented by the ‘≡’ symbol is used. For example, we can write that 3 ≡ 13 (mod 10), 13 ≡ 23 (mod 10), and 3 ≡ 23 (mod 10).
(c) Additive and multiplicative inverse: While working with modular arithmetic, we often need to determine the inverse of an element with respect to some operation. Two commonly required inverses are additive and multiplicative inverses. The former is the inverse with respect to the addition operation, while the latter is the inverse with respect to the multiplication operation.
Each element in modular arithmetic has only one additive inverse, which is always unique; sometimes, the additive inverse of an element is the element itself. Let x and y be two elements of the set Zm. Now, x is said to be the additive inverse of y and vice versa if:
x+y≡0 (mod m)
Simply put, the additive inverse of any element, say x in Zm is equal to m-x. For example, the additive inverse of 11 in Z15={0,1,2,…,13,14} is 4 (15-11).
On the other hand, an element may or may not have a multiplicative inverse. Let x and y be two elements of the set Zm. Now, x is said to the multiplicative inverse of y and vice versa if:
x*y≡1 (mod m)
For example, the multiplicative inverse of 7 in Z15={0,1,2,…,13,14} is 13, as 7*13≡1 (mod 15).
The simple method to determine whether or not a number (x) in Zm has a multiplicative inverse is to compute the GCD of x and m. If gcd(x,m)comes out to be one, x has a multiplicative inverse; otherwise, the multiplicative inverse for x in Zm does not exist. For example, there does not exist a multiplicative inverse for number 5 in Z15 because gcd(5,15)≠ 1. Notice that if gcd(x,m)=1, x and m are said to be relatively prime.
12. Describe the extended Euclidean algorithm to find the multiplicative inverse.
Ans.: The extended Euclidean algorithm is an extension to the Euclidean algorithm. Besides finding the gcd of two positive integers x and y, it simultaneously finds the multiplicative inverses a and b such that:
m*x+n*y=gcd(x,y)
where m is the multiplicative inverse of x mod y and n is the multiplicative inverse of y mod x.
Algorithm
The following are the steps involved in the extended Euclidean algorithm to find the gcd of two positive integers along with the multiplicative inverses are as follows:
1. a:=x
2. b:=y
3. c:=1
4. d:=0
5. e:=0
6. f:=1
7. while (b>0)
{
q:=a/b
r:=a-q*b
a:=b
b:=r
m:=c-q*d
c:=d
d:=m
n:=e-q*f
e:=f
f:=n
}
8. gcd(x,y):=a
9. m:=c
10. n:=e
Similar to the Euclidean algorithm, the extended Euclidean algorithm also uses the reduction process to find the gcd and multiplicative inverses. It uses three sets of variables, (a,b), (c,d), and (e,f) and during each step of the reduction process, three sets of calculations are made, one per each set of variables. To start with, the variables a, b, c, d, e, and f are initialized with x, y, 1, 0, 0, and 1, respectively. In the while loop, variables q and r are used to hold the quotient and the remainder of a divided by b, respectively. Then, variables a and b are updated in a similar manner as in the Euclidean algorithm. The set of variables (c,d) and (e,f) are also updated on the basis of q's value. This process continues until the value of b becomes zero. Finally, we obtain the gcd(x,y) as a as well as the values of m and n.
13. What is an algebraic structure? Also, explain group, ring, and field.
Ans.: An algebraic structure refers to the combination of a set of integers and the operations that are defined on the elements of the set. The commonly used algebraic structures are as follows:
Group
A group (G), denoted as G=<{…},•>, is a set of elements along with a binary operation “•” performed on each ordered pair (x,y) of elements of G such that x•y satisfies the following four properties:
(a) Closure: If both x and y belong to the same group G, then x•y also is in G. That is, if x and y are the elements of the same group, then the result of a binary operation on these elements is another element of that group.
(b) Associativity: If x, y, and z belong to the same group G, then (x•y)•z=x•(y•z). That is, the order of operation does not affect the result.
(c) Existence of identity: For each element x in G, there always exists an identity element e within the same group such that x•e=e•x = x.
(d) Existence of inverse: For each element x in G, there always exists an inverse element x′ within the same group such that x•x′=x′•x=e.
A group that satisfies all the four properties of a group and an additional property called commutativity is said to be an abelian group, also called commutative group. The commutative property states that for all x and y belonging to G, x•y = y•x.
A group that contains a finite number of elements is referred to as a finite group, whereas a group that is not finite is called an infinite group. For example, a group G1=<{1,3,5,7,9},+> is a finite group while a group G2=<Zn,+> where Zn is a set of integers, is an infinite group. The number of elements in a group indicates the order of the group. For example, the order of group G1 is five while the order of group G2 is infinite.
Ring
A ring (R), denoted as R=<{…},•, , is a set of elements with two binary operations, “ >
>•” and “

R is an abelian group with respect to the first operation (•). In other words, R satisfies the closure, associativity, commutativity, existence of identity, and existence of inverse properties with respect to the “•” operation.

R satisfies the closure and associativity properties with respect to the second operation ( ). In addition, the second operation (
). In addition, the second operation ( ) must be distributed over the first operation (
) must be distributed over the first operation (•). The distributivity of the second operation over the first means that if x, b, and c are the elements of ring R, then x (
y•z) = (x )  y
y• (x ) and ( z
zx•y)  z
zx )  z
z• (y ). z
z
A ring is said to be a commutative ring if it satisfies all the properties of a ring plus if the second operation ( ) also satisfies the commutative property, that is for all
) also satisfies the commutative property, that is for all x and y belonging to the ring R, x  y=y
y=y  x
x
Field
A field (F), denoted as F=<{…},•,>, is a set of elements with two binary operations, “•” and “
 ”, such that
”, such that F is a commutative ring where the second operation ( ) satisfies all the five properties defined for the first operation (
) satisfies all the five properties defined for the first operation (•) except that there is no inverse for the identity element of the first operation with respect to the second operation.
14. Explain each finite field of the form GF(pn).
Ans.: A field with a finite number of elements is called a finite field. The finite fields are the most important and most frequently used in cryptography for performing modular arithmetic operations. The concept and theory of finite fields was given by Galois, according to which if a field is finite, then it contains pn number of elements, where p is a prime number and n is a positive integer. Thus, the finite fields are usually known as Galois field and is denoted by GF(pn).
A finite field with n=1 is called the GF(p) field. This field is in fact the set Zp={0,1,…,p-1}, in which two arithmetic operations, addition and multiplication, can be applied. Each element of this set has an additive and multiplicative inverse except zero, which has no multiplicative inverse.
As we know, positive integers are stored in computers in the form of n-bit words, where the value of n can be 8, 16, 32, and so on. This implies that the range of integers that can be stored is 0 to 2n-1 and the modulus is 2n. Now, using the GF(p) finite field with the set Zp, where p is the largest prime number less than 2n-1, would be inefficient as the integers ranging from p to 2n-1 will not be used. To overcome this inefficiency of the GF(p) field, the GF(2n) field is used. This field uses a set of 2n elements, and each element is an n-bit word.
15. Find out the result of the following operations:
(a) 140 mod 10
(b) -73 mod 13
(c) 0 mod 7
Ans.: (a) When 140 is divided by 10, we get the remainder r=0. This means that 140 mod 10=0.
(b) When -73 is divided by 13, we get the remainder r=-8. To make r non-negative, we need to add modulus (13) to r. That is, r =-8+13=5. This means that -73 mod 13=5.
(c) When 0 is divided by 7, we get the remainder r =7. This means that 0 mod 7 = 7.
16. Find the GCD of 2740 and 1760 using the Euclidean algorithm.
Ans.: Using the Euclidean algorithm as explained in Question 9, we have x = 2740 and y = 1760.
Now, initializing a = x and b = y, we get a = 2740 and b = 1760. As b > 0, we move to the first iteration of the while loop.
Algorithm
First iteration
q=2740/1760=1
r=2740-1*1760=980
a=1760
b=980
As 980 > 0, we move to the next iteration.
Second iteration
q=1760/980=1
r=1760-1*980=780
a=980
b=780
As 780 > 0, we move to the next iteration.
Third iteration
q=980/780=1
r=980-1*780=200
a=780
b=200
As 200 > 0, we move to the next iteration.
Fourth iteration
q=780/200=3
r=780-3*200=180
a=200
b=180
As 180 > 0, we move to the next iteration.
Fifth iteration
q=200/180=1
r=200-1*180=20
a=180
b=20
As 20 > 0, we move to the next iteration.
Sixth iteration
q=180/20=9
r=180-9*20=0
a=20
b=0
As the value of b has become zero, the while loop terminates.
Thus, gcd(x, y)=a

gcd(2740, 1760)=20
17. Find the greatest common divisor of 400 and 60 using the extended Euclidean algorithm. Also, find the values of m and n.
Ans.: Using the extended Euclidean algorithm as explained in Question 12, we have x = 400 and y = 60. Now, initializing a = x and b = y, we get a = 400 and b = 60. We also know that c = 1, d = 0, e = 0, and f = 1.
As b>0, we move to the first iteration of the while loop.
First iteration
q = 400/60=6
r = 400-6*60=40
a = 60
b = 40
m = 1-6*0=1
c = 0
d = 1
n = 0-6*1=-6
e = 1
f = -6
As 40 > 0, we move to the next iteration.
Second iteration
q = 60/40=1
r = 60-1*40=20
a = 40
b=20
m = 0-1*1=-1
c = 1
d = -1
n = 1-1*(-6)=7
e = -6
f = 7
As 20 > 0, we move to the next iteration.
Third iteration
q = 40/20=2
r = 40-2*20=0
a = 20
b = 0
m = 1-2*(-1)=3
c = -1
d = 3
n = (-6) -2*7=-20
e = 7
f = -20
As the value of b has become zero, the while loop terminates.
Now, gcd(x, y)=a, m = c, and n = e. Thus, gcd(400, 60)=20, m = -1, and n = 7.
Multiple-choice Questions
1. The conversion of ciphertext into plaintext is known as __________.
(a) Encryption
(b) Decryption
(c) Cryptography
(d) Cryptanalyst
2. Which of the following is a component of cryptography?
(a) Ciphertext
(b) Ciphers
(c) Key
(d) All of these
3. Which of the following is needed to implement a chosen-plaintext attack?
(a) The attacker must have knowledge of the ciphertext.
(b) The attacker must have access to the receiver's computer.
(c) The attacker must have access to the sender's computer.
(d) Both (a) and (b)
4. Which of the following is needed to implement a chosen-ciphertext attack?
(a) The attacker must have knowledge of the ciphertext.
(b) The attacker must have access to the receiver's computer.
(c) The attacker must have access to the sender's computer.
(d) Both (a) and (b)
5. What is a chosen-text attack?
(a) It is a combination of known-plaintext attack and chosen-ciphertext attack.
(b) It is a combination of chosen-plaintext attack and known-ciphertext attack.
(c) It is a combination of known-plaintext attack and known-ciphertext attack.
(d) It is a combination of chosen-plaintext attack and chosen-ciphertext attack.
6. Which of the following are the functions of key management?
(a) Key generation, distribution, and installation
(b) Key storage, key change, and key control
(c) Both (a) and (b)
(d) None of these
7. Which of the following is true in the context of steganography?
(a) It conceals the existence of the message.
(b) It conceals the contents of the message.
(c) It involves less overhead than cryptography.
(d) Both (a) and (b)
8. In public-key cryptography, __________ key is used for encryption.
(a) Public
(b) Private
(c) Both (a) and (b)
(d) Shared
9. The multiplicative inverse of 13 in Z15 is __________.
(a) Five
(b) Seven
(c) Nine
(d) Eight
10. Which of the following properties designates a group as an abelian group?
(a) Closure
(b) Associativity
(c) Distributivity
(d) Commutativity
Answers
1. (b)
2. (d)
3. (c)
4. (d)
5. (d)
6. (c)
7. (a)
8. (a)
9. (b)
10. (d)
1. Define a symmetric-key cipher.
Ans.: A cipher (a combination of encryption and decryption algorithms) that uses the same key for both encryption and decryption is referred to as a symmetric-key cipher.
2. Explain the symmetric cipher model.
Or
Explain the conventional encryption model.
Ans.: A symmetric cipher model (also referred to as a conventional encryption model) consists of various components (see Figure 3.1), which are described as follows:
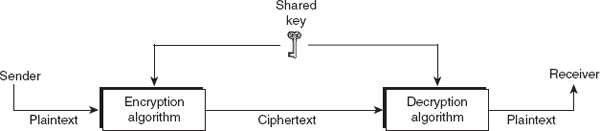
Figure 3.1 Symmetric Cipher Model
(a) Plaintext: This refers to the original message that the sender wishes to send securely. It is an input to the encryption algorithm.
(b) Encryption algorithm: This algorithm applies various substitutions and transpositions on the plaintext, with the help of a secret key, to transform it into an unintelligible form. The encryption algorithm is used at the sender's end.
(c) Ciphertext: This refers to the coded (scrambled) message that is produced by the encryption algorithm. The ciphertext is sent to the receiver through a communication channel.
(d) Decryption algorithm: This is the opposite of an encryption algorithm. It is used at the receiver's end to convert ciphertext back into plaintext (original message). The encryption and decryption algorithms are together known as ciphers.
(e) Secret (shared) key: This usually refers to a number or a set of numbers on which the cipher operates. Both encryption and decryption algorithms use the same key (shared between the sender and receiver) to encrypt or decrypt the messages, respectively.
3. What are the issues in a conventional encryption model?
Ans.: Though conventional encryption is fast, efficient and excellent for large data transmissions such as file transfers, it suffers from certain limitations, which are as follows:
 As the sender and receiver share a single key, the key must be sent via a secure channel. However, if such a secure channel already exists, the question then arises as to why encryption was required in the first place.
As the sender and receiver share a single key, the key must be sent via a secure channel. However, if such a secure channel already exists, the question then arises as to why encryption was required in the first place.
 Exchanging the secret key using unsecure channels such as telephone lines, which are prone to eavesdropping, may violate the confidentiality of the key.
Exchanging the secret key using unsecure channels such as telephone lines, which are prone to eavesdropping, may violate the confidentiality of the key.
 There are some organizations that deal with thousands or million's of clients on a daily basis. In such organizations, it is extremely difficult to assign a unique key to each client.
There are some organizations that deal with thousands or million's of clients on a daily basis. In such organizations, it is extremely difficult to assign a unique key to each client.
4. What are the different categories of classical encryption techniques?
Ans.: The classical encryption techniques, also referred to as traditional symmetric-key ciphers, are divided into two categories: substitution ciphers and transposition ciphers.
 Substitution cipher: This cipher replaces a symbol (a single letter or a group of letters) of the plaintext with another symbol. For example, the letter
Substitution cipher: This cipher replaces a symbol (a single letter or a group of letters) of the plaintext with another symbol. For example, the letter A can be replaced with letter C, and letter P with letter Z. If the symbols are digits, then the digit 2 can be replaced by digit 5, and digit 3 with digit 6. Substitution ciphers are further categorized into monoalphabetic ciphers and polyalphabetic ciphers.
 Transposition cipher: In this cipher, there is no substitution of characters; rather, the location of characters in plaintext is changed to form the ciphertext. In other words, a transposition cipher reorders (transposes) the symbols in the plaintext, thereby creating the ciphertext. Thus, the order of characters in the plaintext is no longer preserved in the ciphertext. For example, a symbol at the third position in the plaintext may be placed at the eighth position in the ciphertext, or a symbol at the fifth position in the plaintext may appear at the fifteenth position in the ciphertext. Transposition ciphers are further categorized into keyless transposition ciphers and keyed transposition ciphers
Transposition cipher: In this cipher, there is no substitution of characters; rather, the location of characters in plaintext is changed to form the ciphertext. In other words, a transposition cipher reorders (transposes) the symbols in the plaintext, thereby creating the ciphertext. Thus, the order of characters in the plaintext is no longer preserved in the ciphertext. For example, a symbol at the third position in the plaintext may be placed at the eighth position in the ciphertext, or a symbol at the fifth position in the plaintext may appear at the fifteenth position in the ciphertext. Transposition ciphers are further categorized into keyless transposition ciphers and keyed transposition ciphers
5. What is a monoalphabetic cipher? Explain different techniques of monoalphabetic ciphers.
Ans.: A monoalphabetic cipher is a substitution cipher where a symbol in the plaintext has a one-to-one relationship with a symbol in the ciphertext. It means that a symbol in the plaintext is always replaced with the same symbol in the ciphertext, irrespective of its position in the plaintext. The different techniques based on monoalphabetic ciphers are as follows:
Additive cipher
This is the easiest and simplest monoalphabetic cipher, where each letter in plaintext is coded by shifting a certain number of spaces from it. For this, it uses a key that defines the number of spaces to be shifted. In this technique, each character in the plaintext is first assigned a numeric value according to its position in Z26, the set of alphabets. For example, a (or A) will be assigned 0, b (or B) will be assigned 1, c (or C) will be assigned 2, and so on. The key (say, K) used for encrypting the plaintext is also an integer in Z26.
At the sender's end, the key (K) is added to plaintext (say, P) and the result is mapped to Z26, using the modular arithmetic to form the ciphertext (say, C), as shown here.
C = (P + K) mod 26
At the receiver's end, the reverse process is followed for converting the ciphertext back to plaintext. That is, the additive inverse of key K in Z26, denoted as -K, is added to ciphertext (C) and the result is mapped to Z26 using the modular arithmetic to obtain plaintext (P), as shown here.
P = (C - K) mod 26
Figure 3.2 depicts the process of encryption and decryption in additive cipher. An example given in Question 17 illustrates the encryption and decryption processes using additive cipher.
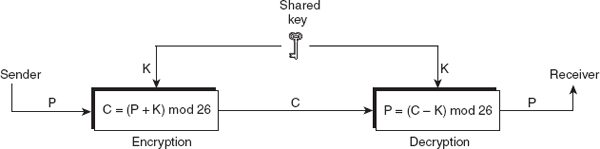
Figure 3.2 Additive Cipher
Shift cipher
In this cipher, an encryption algorithm can be interpreted as ‘a shift by a key number of characters in the clockwise direction, that is, towards the end of the alphabet’ while a decryption algorithm can be interpreted as ‘a shift by a key number of characters in the anti-clockwise direction, that is, towards the beginning of the alphabet’. For example, for key = 5, the encryption algorithm moves five characters down in the set of alphabets (Z26), while the decryption algorithm moves five characters up the alphabet in the set of alphabets. Notice that during encryption and decryption, as the end or the beginning of the alphabet is reached, we wrap round. For the same value of the key K, both shift and additive ciphers produce the same ciphertext; thus, traditionally, additive ciphers have also been referred to as shift ciphers.
Caesar cipher
This cipher has been named after its inventor, Julius Caesar. It is simply an additive cipher with key = 3. That is, during encryption, each plaintext character is replaced with a character obtained by moving three places down in the alphabet and the reverse happens during decryption. Like shift cipher, on reaching the end or beginning of the alphabet, we wrap around. The simplicity of Caesar cipher becomes its weakness as anyone can determine the plaintext by just replacing each ciphertext character with a character obtained by moving three characters up in the alphabet.
To overcome this limitation of Caesar cipher, its enhanced version, named modified Caesar cipher, was proposed. In this cipher, a character can be replaced with any other character. However, as we know, the English alphabet has only 26 characters; hence, a character can be replaced only with one of the other 25 characters. Thus, the cipher is vulnerable to the brute-force attack, as an attacker just needs to choose one out of 25 possible characters.
Multiplicative cipher
In this cipher, the plaintext is encrypted by multiplying it with the key, while the ciphertext is decrypted by performing division on it with the key(K). Since the operations are in Z26, the result needs to mapped to Z26 using modular arithmetic. Moreover, division by key during decryption implies multiplication by the multiplicative inverse of the key in Z26 (denoted as K-1). The following are the formulae used to encrypt the plaintext (and) P decrypt the ciphertext(C), respectively.
C = (P * K) mod 26
P = (C * K-1) mod 26.
Figure 3.3 depicts the process of encryption and decryption in a multiplicative cipher. The example given in Question 17 illustrates encryption and decryption using multiplicative cipher.
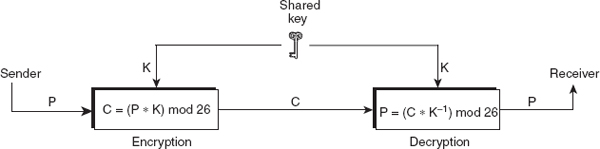
Figure 3.3 Multiplicative Cipher
Affine cipher
Affine cipher is the combination of additive and multiplicative ciphers with a pair of keys. Two ciphers are applied one after another, and a separate key is used for each. The first key of the key-pair is used for the first cipher (either additive or multiplicative), while the second key is used for the other. The process of encryption and decryption in affine cipher is shown in Figure 3.4.
Figure 3.4 Affine Cipher
At the sender's side, the plaintext (P) is first encrypted using the multiplicative cipher and key K1 to obtain the temporary ciphertext (C1), as shown here:
C1 = (P * K1) mod 26
Then, the ciphertext C1 is again encrypted using the additive cipher and key K2 to obtain the final ciphertext (C), as shown here:
C = (C1 + K2) mod 26.
At the receiver's side, the algorithm first decrypts the received ciphertext (C) using the additive cipher and additive inverse of the key K2 in Z26 (denoted as -K2) to obtain a temporary plaintext (P1), as shown here:
P1 = (C - K2) mod 26
Then, the plaintext P1 is again decrypted using the multiplicative cipher and multiplicative inverse of the key K1 in Z26 (denoted as K1-1) to obtain the original plaintext(P), as shown here:
P = (P1 * K1-1) mod 26.
It should be noted that, if the second cipher is the additive cipher in encryption, then the additive inverse should be the first cipher in decryption. In the same way, if the second cipher is the multiplicative cipher in encryption, then the multiplicative inverse should be the first cipher in decryption. An example given in Question 17 illustrates the encryption and decryption processes using the affine cipher.
6. What is polyalphabetic cipher? Also, explain the different techniques of using the polyalphabetic cipher.
Ans.: In polyalphabetic cipher, the characters in the plaintext may have a one-to-many relationship with the characters in the ciphertext. This means that the same character appearing in plaintext can be replaced with a different character in the ciphertext. For example, ‘hello’ can be encrypted to ARHIF using a polyalphabetic cipher. That is, the two occurrences of the letter ‘l’ in the plaintext are replaced with different characters. Due to the one-to-many relationship between the characters of plaintext and ciphertext, the key used must indicate which of the possible characters can be used for replacing a character in the plaintext. For this, the plaintext is divided into groups of characters, and a set of keys K =(K1, K2, K3,…)is used for encrypting the groups of plaintext, such that the ith key(Ki)is used to encrypt the ith character of a plaintext group. The different techniques based on polyalphabetic ciphers are as follows:
Autokey cipher
In this cipher, the key used is a group of subkeys (K1, K2, K3,…, Kn), where each subkey is used to encrypt the corresponding character in the plaintext. That is, the first subkey is used to encrypt the first plaintext character, the second subkey is used to encrypt the second plaintext character and so on. The cipher is named so because the subkeys are generated automatically during the encryption process. The first subkey is predetermined; its value is chosen by the sender and the receiver. The second subkey is the value of the first plaintext character, the third subkey is the value of the second plaintext character and so on.
At the sender's end, a plaintext character (say, Pi) is added with the respective subkey (Ki), and the result is mapped to Z26, using modular arithmetic to obtain the corresponding ciphertext character (Ci), as shown here:
Ci = (Pi + Ki) mod 26
At the receiver's end, the reverse process is followed to decrypt the ciphertext. That is, a ciphertext character (say, Ci) is added with the additive inverse of the respective subkey (denoted as, -Ki) and the result is mapped to Z26 using the modular arithmetic to obtain the corresponding plaintext character (Pi) as shown here:
Pi = (Ci - Ki) mod 26
An example given in Question 18 illustrates the encryption and decryption processes using the autokey cipher.
Playfair cipher
The Playfair cipher, also known as Playfair square, was used by the British army during World War I, and then by Australians during World War II. Despite its invention by Wheatstone in 1854, it is popularly known after the name of Lord Playfair, who heavily promoted its use. Here, the secret key is formed of 25 alphabets organized into a 5 × 5 matrix. (I and J are considered as same and inserted in the same cell in the matrix.) Different keys can be obtained from different possible arrangements of alphabets in the matrix.
The first step in the Playfair encryption technique is to create and populate the matrix. Initially, a keyword (or phrase) is chosen by the sender and receiver that may not necessarily contain all the 25 alphabets. To organize this keyword in the matrix, it is entered starting from the top left position to right (that is, row-wise), and from top to bottom. While entering, the duplicate letters in the keyword are dropped; that is, each letter of the keyword is entered only once. The remaining empty positions of the keyword matrix are filled with the alphabets (in order) that are not included in the keyword. Moreover, if either I or J appears in the keyword, both are ignored while filling the empty positions of the matrix. However, if neither I nor J appears in the keyword, both are placed at the same position in the matrix. This organization of 25 alphabets in the matrix becomes the secret key for encryption and decryption.
The next step is to encrypt the plaintext. However, before encryption, the plaintext message is broken into diagraphs (group of two characters). If both characters in a pair are the same, then we insert a bogus letter (say, X) between them to distinguish. In case the plaintext consists of an odd number of characters, then also a bogus character is inserted at the end of the plaintext to make the number of characters even. For example, if the plaintext is GREETING, then we have four groups of two letters each as GR, EE, TI, and NG. As the second pair of the message contains repeated letter E, the bogus letter X is inserted between two E's. Now, the pairs of the message become GR, EX, ET, IN and G. To make the number of characters even, the bogus character X is inserted at the end, making the last pair as GX.
At the sender's end, each pair of alphabets in the plaintext is encrypted using the following rules:
 If the two letters in a pair appear in the same row of the keyword matrix, they must be replaced with the letters at their immediate right positions. We must wrap around to the beginning of the row if the any of the letters appears at the end of the row.
If the two letters in a pair appear in the same row of the keyword matrix, they must be replaced with the letters at their immediate right positions. We must wrap around to the beginning of the row if the any of the letters appears at the end of the row.
 If the two letters in a pair appear in the same column of the keyword matrix, they must be replaced with the letters at their immediate below positions. We must wrap around to the beginning of the column if any of the letters is the last letter in the column.
If the two letters in a pair appear in the same column of the keyword matrix, they must be replaced with the letters at their immediate below positions. We must wrap around to the beginning of the column if any of the letters is the last letter in the column.
 If the two letters in a pair do not appear in the same row or column of the keyword matrix, each of them must be replaced with the letter placed at the intersecting position of its own row and the column of another.
If the two letters in a pair do not appear in the same row or column of the keyword matrix, each of them must be replaced with the letter placed at the intersecting position of its own row and the column of another.
At the receiver's end, the ciphertext is decrypted using the same rules as for encryption, with some differences. If the two letters of a pair in the ciphertext satisfy the condition of rule 1, they are replaced with the letters at their immediate left positions. If the two letters of a pair in the ciphertext satisfy the condition of rule 2, they are replaced with the letters at their immediate above positions. The rule 3 is same for decryption. During decryption, the bogus letters are also removed. An example given in Question 19 illustrates the encryption and decryption processes using the Playfair cipher.
Vigenere cipher
The Vigenere cipher has been named after its designer Blaise de Vigenere. In this cipher, the group of subkeys used depends on the position of the characters in the plaintext, rather than the character itself. Thus, the group of subkeys can be created independent of the plaintext. The initial secret key of length n (where 1 ≤ n ≤ 26) is chosen by the sender and receiver. Then, the chosen key is repeated till the end of the plaintext. That is, if the initial secret key chosen is(K1, K2,…, Km), then the set of keys used for encryption and decryption will be K=[(K1, K2,…, Km), (K1, K2,…, Km),…]. Thus, this cipher helps to encrypt plaintext of any size.
At the sender's end, each plaintext character (Pi) is added with the respective key character (Ki) and the result is mapped to Z26 using the modular arithmetic to obtain the corresponding ciphertext character (Ci) as shown here:
Ci = (Pi + Ki) mod 26
At the receiver's end, the reverse process is followed to decrypt the ciphertext. That is, a ciphertext character (say, Ci) is added with the additive inverse of the respective key character (denoted as, -Ki) and the result is mapped to Z26 using the modular arithmetic to obtain the corresponding plaintext character (Pi) as shown here:
Pi = (Ci - Ki) mod 26
An example given in Question 20 illustrates the encryption and decryption processes using the Vigenere cipher.
Hill cipher
The Hill cipher was invented in 1929 by Lester S. Hill, and it is named after him. In the Hill cipher, the plaintext is first divided into equal-size blocks. Then, the blocks are encrypted in such a way that each block element (character) participates in the encryption of other block elements in the block. The key (K) used in the Hill cipher is in the form of an n×n square matrix, where n is the block size (see Figure 3.5). Each element of the key matrix is represented as Kij, where 1 ≤ i, j ≤ n.
Figure 3.5 Key Matrix
Consider a plaintext block (P) that contains n characters is to be encrypted. Let P1, P2,…, Pn represent the plaintext characters in this block and their corresponding ciphertext characters are represented as C1, C2,…, Cn. Then, we get the ciphertext as shown here:
C1 = (P1K11 + P2K21 + … + PnKn) mod 26C2 = (P1K12 + P2K22 + … + PnKn2) mod 26...Cm = (P1K1n + P2K2n + … + PnKnn) mod 26
The preceding equations can be expressed as:
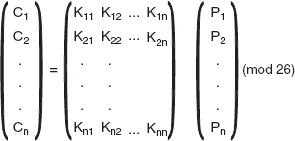
In general, the encryption in the Hill cipher can be expressed as shown here:
C = K P mod 26
To perform decryption at the receiver's end, the inverse of the key is first determined in Z26, and then the ciphertext is decrypted, as shown here:
P = K-1 C mod 26
An example given in Question 21 illustrates the encryption and decryption processes using the Hill cipher.
7. What are keyless and keyed transposition ciphers?
Ans.: Keyless and keyed ciphers are two categories of transposition ciphers that reorder (permute) the symbols of plaintext to form ciphertext. These are described as follows:
 Keyless transposition ciphers: These are the traditional ciphers, and are easy to use. They do not use any key to permute the characters in the plaintext and thus, are named as keyless ciphers. To permute the characters, the plaintext characters are written in a table either column-wise or row-wise. In the former case, ciphertext is formed by reading the characters from the table row-wise, while in the latter case, column-wise.
Keyless transposition ciphers: These are the traditional ciphers, and are easy to use. They do not use any key to permute the characters in the plaintext and thus, are named as keyless ciphers. To permute the characters, the plaintext characters are written in a table either column-wise or row-wise. In the former case, ciphertext is formed by reading the characters from the table row-wise, while in the latter case, column-wise.
 Keyed transposition ciphers: These ciphers make use of a key to permute the characters in the plaintext and, thus, are named as keyed ciphers. These ciphers first divide the plaintext into blocks of predefined size, and then a key is used to permute the characters within each block individually.
Keyed transposition ciphers: These ciphers make use of a key to permute the characters in the plaintext and, thus, are named as keyed ciphers. These ciphers first divide the plaintext into blocks of predefined size, and then a key is used to permute the characters within each block individually.
8. Write a short note on columnar transposition ciphers.
Ans.: A columnar transposition cipher is the combination of keyless and keyed transposition ciphers. It performs encryption and decryption in three steps; the first and third steps are keyless, while the second step is performed on the basis of a key. The plaintext characters are first arranged in the table row-wise. Secondly, these characters are permuted by reordering the columns based on a key. And, finally, the characters are read from the new table column-wise.
To understand, consider the plaintext ‘hellohowareyou', and the key ‘BACKIN’. Initially, the plaintext characters are arranged in the table row-wise, as shown in the following. The rows are padded with extra characters to fill the table, if required.
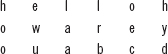
After arranging the plaintext, the letters of the key BACKIN are numbered according to the alphabetical order. For example, A is assigned the number 1, B is 2, C is 3, I is 4, K is 5 and N is 6. Now, the columns of the table are reordered according to numbers assigned to the key letters. For example, the column 1 is interchanged with column 2, column 4 with column 5, while columns 3 and 6 remain intact. After reordering the columns, the new table is as shown in the following:
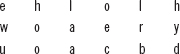
The characters are now read out column-wise from the new table to form the ciphertext. That is, the ciphertext is ‘ewuhoolaaoeclrbhyd’.
9. What is the difference between stream cipher and block cipher?
Ans.: Stream cipher and block cipher are two categories of symmetric ciphers.
 Stream cipher: This cipher operates on one symbol (character) of plaintext at a time and produces a corresponding symbol of ciphertext. As the name of the cipher implies, we have a plaintext stream
Stream cipher: This cipher operates on one symbol (character) of plaintext at a time and produces a corresponding symbol of ciphertext. As the name of the cipher implies, we have a plaintext stream P =(P1,P2,P3,…), a ciphertext stream C=(C1,C2,C3,…), and a key stream K=(K1, K2, K3,…). The plaintext characters are input into the encryption algorithm, one character at a time. The encryption algorithm uses the respective subkey to encrypt each plaintext character, which results in a corresponding ciphertext character. Each character is encrypted and decrypted using the same key, regardless of the fact that multiple keys are being used. For example, consider that the plaintext is ‘user’ and the key stream used is (K1, K2 and K3). Now, the plaintext is encrypted such that the characters ‘u’ and ‘r’ are encrypted using the key K1, the characters ‘s’ is encrypted using the key K2 and the character ‘e’ is encrypted using K3. During decryption also, the same set of keys (K1, K2 and K3) is used, such that the characters ‘u’ and ‘r’ are decrypted using the key K1, the character ‘s’ is decrypted using the key K2 and the character ‘e’ is decrypted using the key K3. The Additive cipher and Vigenere cipher can be categorized as stream ciphers.
 Block cipher: This cipher encrypts a group or block (with size > 1) of symbols in plaintext at one time, producing a block of ciphertext of the same size. Similarly, during decryption, a block of ciphertext symbols is converted back to a block of plaintext with one block at a time. A single key is used to encrypt or decrypt the entire block, even if the key contains multiple values. The Hill cipher and Playfair cipher can be categorized as block ciphers.
Block cipher: This cipher encrypts a group or block (with size > 1) of symbols in plaintext at one time, producing a block of ciphertext of the same size. Similarly, during decryption, a block of ciphertext symbols is converted back to a block of plaintext with one block at a time. A single key is used to encrypt or decrypt the entire block, even if the key contains multiple values. The Hill cipher and Playfair cipher can be categorized as block ciphers.
10. Explain the term one time pad.
Ans.: The one-time pad (also known as the Vernam cipher) was first implemented at AT&T using a device called the Vernam machine. It is actually a random set of non-repeating characters that is used as a key for generating the ciphertext message. As the name suggests, the set of characters can be used only once and, therefore, cannot be used for any other message. The algorithm used in generating a ciphertext message by the one-time pad scheme is as follows:
1. The alphabets in the plaintext are assigned numbers in an increasing order. For example, A = 0, B = 1,…, and Z = 25.
2. The one-time pad alphabets are randomly chosen, and numbers are assigned in the same manner as in the plaintext. For example, C = 2, D = 3 and so on.
3. The numbers that correspond to the plaintext and the one-time pad input are added.
4. Then the mod 26 operation is done with each generated character of the sum.
5. The numbers obtained from the sum are translated back to the corresponding alphabet, which gives the output ciphertext.
The security of the one-time pad method is very high because of its randomness and one-time use. Thus, it can only be used for small plaintext messages. The ciphertext message generated using the one-time pad method is also random; that is, the same ciphertext message is not generated for two same plaintexts, thus making it less vulnerable to attacks. In spite of these benefits, it faces some difficulties in practical implementation. One problem is that it is difficult to generate a large set of random numbers each time for the same nodes to communicate with each other. Another problem is that of key distribution and protection, as a key of equal length is needed by both the sender and the receiver in every message exchange. An example illustrating the use of one-time pad is shown in Question 22.
11. What do you understand by bit-oriented ciphers? Why do we need them?
Ans.: The ciphers that perform encryption or decryption at the bit level rather than at the character level are referred to as bit-oriented ciphers. Earlier, most of the information to be encrypted was in textual form; thus, the use of character-oriented ciphers was justified. However, these days, the information to be encrypted is not just text, but may comprise graphics, audio and video. Thus, bit-oriented ciphers are needed, because such types of data can be conveniently transformed into streams of bits, which can then be encrypted and sent to the intended receiver. Moreover, as the text is treated at the bit level, each character of plaintext can be replaced with 8 bits or 16 bits. This increases the number of symbols in the plaintext by 8 or 16 times, thereby also increasing the security.
12. What do you mean by modern block cipher? What are its components?
Ans.: The modern block cipher is a bit-oriented symmetric-key cipher that encrypts an m-bit block of plaintext at a time to produce an m-bit block of ciphertext. Similarly, during decryption, an m-bit block of ciphertext is converted back to an m-bit block of plaintext, one block at a time. Each block of bits is encrypted or decrypted using the k-bit key (see Figure 3.6). The decryption algorithm used is the inverse of the encryption algorithm, and the same secret key is used for both encryption and decryption. Thus, the same block of plaintext is always encrypted to same block of ciphertext.
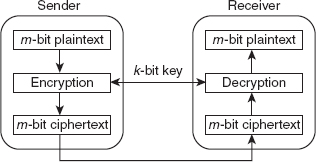
Figure 3.6 Modern Block Cipher
If the plaintext contains less than m bits, extra bits (padding) are added to make it an m-bit block. On the other hand, if the plaintext contains more than m bits, the plaintext is divided into blocks of m bits each and extra bits are added to the last block to make it an m-bit block if it contains less than m bits.
The modern block cipher consists of various components, described as follows:
 S-box: This is a substitution box having the same characteristics as that of the substitution cipher, except that the substitution of several bits is performed in parallel. It takes
S-box: This is a substitution box having the same characteristics as that of the substitution cipher, except that the substitution of several bits is performed in parallel. It takes n bits of plaintext at a time as input and produces m bits of ciphertext as output, where the value of n and m may be the same or different. An S-box can be keyed or keyless. In a keyed S-box, the mapping of n inputs to m outputs is decided with the help of a key, whereas in a keyless S-box, the mapping from inputs to outputs is predetermined. Usually, keyless S-boxes are used in modern block ciphers.
 P-box: This is a permutation box having the same characteristics as that of the traditional transposition cipher, except that it performs transposition at the bit-level, and that transposition of several bits is performed at the same time. The input bits are permuted to produce the output bits. For example, the first input bit can be the second output bit, the second input bit can be the third output bit and so on. A P-box is sometimes also referred to as a D-box (diffusion box). It is normally a keyless cipher and can be classified into the following three types (see Figure 3.7), based on the length of input and output:
P-box: This is a permutation box having the same characteristics as that of the traditional transposition cipher, except that it performs transposition at the bit-level, and that transposition of several bits is performed at the same time. The input bits are permuted to produce the output bits. For example, the first input bit can be the second output bit, the second input bit can be the third output bit and so on. A P-box is sometimes also referred to as a D-box (diffusion box). It is normally a keyless cipher and can be classified into the following three types (see Figure 3.7), based on the length of input and output:
 Straight P-box: This P-box takes
Straight P-box: This P-box takes n bits as input, permutes them and produces n bits as output. As the number of inputs and outputs is the same, there are a total of n! ways to map n inputs to n outputs.
 Compression P-box: This P-box takes
Compression P-box: This P-box takes n bits as input and permutes them in such a way that an output of m bits is produced, where m < n. This implies that some of the inputs are blocked and do not reach the output. Compression P-boxes are used in those situations where we need to permute the bits and at the same time need lesser number of bits at each successive stage.
 Expansion P-box: This P-box takes
Expansion P-box: This P-box takes n bits as input and permutes them in such a way that an output of m bits is produced, where m > n. This implies that a single input is mapped to more than one output. The expansion P-boxes are used in those situations where we want a higher number of bits at each successive stage.
 Circular shift: Another important component involved in modern block cipher is the circular shift operation, which tends to conceal the bit patterns in a transmitted word. The bits can be shifted either in the left or the right direction. In a circular left shift operation [see Figure 3.8 (a)], every bit of an
Circular shift: Another important component involved in modern block cipher is the circular shift operation, which tends to conceal the bit patterns in a transmitted word. The bits can be shifted either in the left or the right direction. In a circular left shift operation [see Figure 3.8 (a)], every bit of an m-bit word is shifted by a specific number of positions (say, n) in the left direction. In other words, the n leftmost bits of the word are removed and placed at the rightmost positions. The reverse happens in a circular right-shift operation [see Figure 3.8 (b)], where each bit of an m-bit word is shifted by n positions in the right direction. That is, the n rightmost bits of the word are removed and placed at the leftmost position. The circular shift operation can be either keyed or keyless. In the former case, the key defines the number of positions by which the bits are to be shifted. On the other hand, in the latter case, the number of positions to be shifted is usually fixed and predetermined. It is important to note that if a circular left shift operation is used in encryption, then a circular right shift operation is used in decryption, and vice-versa. Thus, both these operations are inverses of each other.
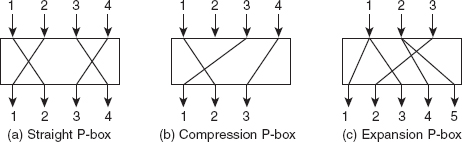
Figure 3.7 Types of P-Boxes
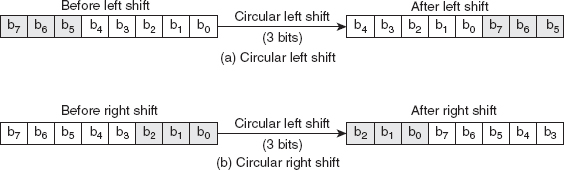
Figure 3.8 Circular Shift Operati
13. Explain Shannon's theory of diffusion and confusion.
Ans.: The theory of diffusion and confusion was proposed by Claude Shannon in attempt to thwart cryptanalysis based on statistical analysis. Both diffusion and confusion are the essential properties of block ciphers. Diffusion is based on the idea of hiding the relationship between the ciphertext and plaintext. This will frustrate a cryptanalyst who examines the ciphertext statistics in order to determine the plaintext. To achieve diffusion, a ciphertext symbol must depend on some or all symbols in the plaintext. That is, a change in a single symbol in the plaintext causes change in several or all symbols in the ciphertext.
On the other hand, confusion is based on the idea of hiding the relationship between the ciphertext and the key. This will frustrate a cryptanalyst who attempts to determine the key using the ciphertext. To prevent intruders from discovering the key, confusion attempts to make the relationship between the value of encryption key and the statistics of ciphertext as complex as possible. This can be achieved by making sure that a ciphertext symbol depends on some or all symbols of the key used. That is, a change in a single bit of the key causes changes in several or all symbols in the ciphertext.
14. What is a product cipher?
Ans.: The concept of product cipher was proposed by Shannon. The basic idea of a product cipher is to build a complex cipher by combining two or more ciphers (transformations) in such a manner that the resulting cipher is more secure than the individual components. That is, various transformations, including substitutions, permutations, circular shifts and transposition, are combined within a single unit to make a complex cipher, known as product cipher. The complexity of a product cipher makes it more secure and resistant to various attacks, thereby making it more difficult for a cryptanalyst to thwart the security. All modern ciphers are product ciphers, and are classified into two categories on the basis of the type of components used in them, namely, Feistel and non-Feistel ciphers.
15. Explain Feistel cipher and its structure.
Ans.: The Feistel cipher, proposed by Horst Fiestel, belongs to a class of product ciphers that permits the use of invertible as well as noninvertible components. The Feistel cipher uses three types of components (units), namely, self-invertible, invertible and noninvertible components. This cipher works by combining all noninvertible units into a single unit and then using the same unit in encryption and decryption algorithms. Now, the problem is that since both encryption and decryption algorithms use noninvertible units, how can they be the inverses of each other? To resolve this problem, we use the XOR operation, so that the effects of a noninvertible component in encryption can be cancelled out during decryption.
Initially, a basic model of the Fiestel cipher was proposed, which had certain shortcomings. To overcome these shortcomings, the basic model was improved, resulting in the final design. Here, we will discuss both the designs.
Basic model
In this structure, the plaintext is divided into two equal-length blocks: left and right. During encryption, a noninvertible function (f), which accepts key (K) as an input, is applied to the right block of the plaintext (denoted as Rp), and the resultant output is XOR-ed with the left block (denoted as Lp). The output of the XOR operation becomes the left block of the ciphertext (denoted as Lc), while the right block of ciphertext (denoted as Rc) is same as the right block of plaintext. The function f and the XOR operation together are referred to as the mixer, which is self-invertible in nature. During decryption, the reverse process is followed. However, the input to the function f remains the same in both the encryption and decryption processes, as shown in Figure 3.9.
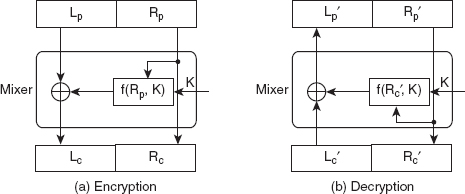
Figure 3.9 Basic Model of Fiestel Cipher
To verify the correctness of the design, we need to ensure that the encryption and decryption algorithms are inverses of each other. That is, it must be proved that Lp = Lp' and Rp = Rp'. To prove this, let us assume that there is no change in the ciphertext during transmission, which means Lc = Lc' and Rc=Rc'. As Rc = Rp and Rc' = Rp', we have Rp' = Rp.
Now, we can write that

As we know that Lc = Lp and  f(Rp,K)
f(Rp,K)Rc = Rp, the equation (1) can be written as:

Hence, the decryption algorithm produces the same plaintext as used by the encryption algorithm. In other words, the encryption and decryption algorithms are the inverses of each other.
Final design of the Feistel cipher
In the basic model of the Feistel cipher, the right block of the plaintext never changes and remains the same in the ciphertext also. Due to this, the generated ciphertext becomes vulnerable to attacks and is more prone to interception by a hacker. Thus, the design was improved by including the following enhancements:
 The number of rounds was increased in the final design.
The number of rounds was increased in the final design.
 A new element called swapper was added to each round. The role of the swapper is to swap the left and right blocks in each round. In addition, the effect of the swapper during encryption is cancelled out with the effect of the swapper during decryption.
A new element called swapper was added to each round. The role of the swapper is to swap the left and right blocks in each round. In addition, the effect of the swapper during encryption is cancelled out with the effect of the swapper during decryption.
 Two round keys (
Two round keys (K1 and K2) are used during encryption and decryption. The encryption and decryption algorithms use the keys in reverse order.
Figure 3.10 shows the final design of the Feistel cipher with two rounds.
The mixers and swappers used in encryption and decryption are inverses of each other, respectively. This implies that the encryption and the decryption algorithms are also inverses of each other. To prove this fact, we need to show that Lp = Lp' and Rp = Rp'. To prove this, let us assume that there is no change in the ciphertext during transmission, which means Lc = Lc' and Rc = Rc'. First, we will prove the equality between the middle texts (L and L', R and R'), and then between the final text. As R' = Lc', Lc' = Lc and Lc = R, we have R' = R.
We can write that:

As we know that Rc= and  f(R,K2)
f(R,K2)Lc=R, Equation (2) can be written as:
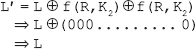
Now, we have Rp'=L', L'=L and L=Rp. Thus, it is proved that Rp' = Rp.
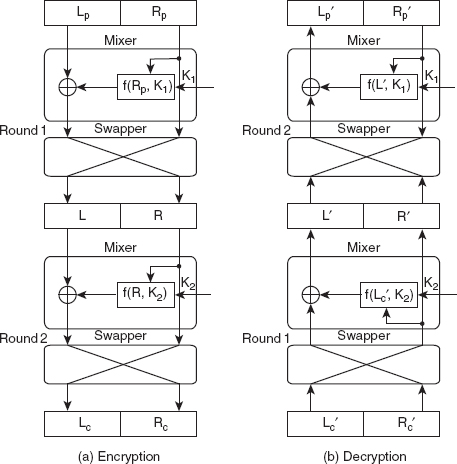
Figure 3.10 Final Design of Fiestel Cipher with two Rounds
We can also write that:

As R'=R and L'=L, Equation (3) can be written as:

As we know that L=Rp and R=Lp, Equation (4) can be written as: f(Rp,K1)
f(Rp,K1)
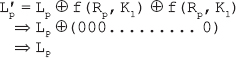
Hence, the decryption algorithm produces the same plaintext as used by the encryption algorithm. In other words, encryption and decryption algorithms are the inverses of each other.
16. What is a non-Feistel cipher?
Ans.: A non-Feistel cipher uses only invertible components. Each element in the plaintext has a respective element in the cipher. For example, if an S-box is used, then it must have the same number of inputs and outputs. In addition, only the straight P-boxes can be used, because the compression and expansion P-boxes are non-invertible in nature. Unlike the Fiestel cipher, it is not required to break the plaintext into two halves in a non-Fiestel cipher.
17. Encrypt the message ‘this is an exercise’ using the following ciphers. Ignore the spaces between the words while encrypting. Also, decrypt the message to get the original plaintext.
(a) Additive cipher with key = 20
(b) Multiplicative cipher with key = 15
(c) Affine cipher with key = (15, 20)
Ans.: (a) Additive cipher with key = 20
Plaintext (P) = ‘this is an exercise’
Key (K) = 20
 Encryption: In additive cipher, the ciphertext
Encryption: In additive cipher, the ciphertext (C) = (P + K) mod 26, which can be found as follows:

Hence, the corresponding ciphertext is ‘nbcmcmuhyrylwcmy’.
 Decryption: To decrypt the ciphertext (
Decryption: To decrypt the ciphertext (C), we first need to determine the additive inverse of 20 in Z26, which is equal to 6 (26–20). Now, the ciphertext (C) can be decrypted to obtain the plaintext (P) using the formula (C+6) mod 26, as shown here:

(b) Multiplicative cipher with key = 15
Plaintext (P) = ‘this is an exercise’
Key (K) = 15
 Encryption: In multiplicative cipher, the ciphertext
Encryption: In multiplicative cipher, the ciphertext (C) = (P * K) mod 26, which can be found as follows:

Hence, the corresponding ciphertext is ‘zbqkqkanihiveqki’.
 Decryption: To decrypt the ciphertext, first we need to determine the multiplicative inverse of 15 in
Decryption: To decrypt the ciphertext, first we need to determine the multiplicative inverse of 15 in Z26, which is equal to 7, as 15 * 7 ≡ 1 (mod 26). Now, the ciphertext (C) can be decrypted to obtain the plaintext (P) using the formula (C * 7) mod 26, as shown here:

(c) Affine cipher with key = (15, 20)
Plaintext (P) = ‘this is an exercise’
Key (K) = 15
 Encryption: In affine cipher, the plaintext (
Encryption: In affine cipher, the plaintext (P) is first encrypted using the multiplicative cipher and the first key (that is, 15) to produce the temporary ciphertext (C1). Then, C1 is again encrypted using the additive cipher and the second key (that is, 20) to produce the final ciphertext(C), as shown here:

Hence, the corresponding ciphertext is ‘tvkekeuhcbcpykec’.
 Decryption: First, the ciphertext (
Decryption: First, the ciphertext (C) is decrypted using the additive cipher and the additive inverse of key 20 to produce the temporary plaintext P1. Then, P1 is again decrypted using the multiplicative cipher and the multiplicative inverse of key 15. The additive inverse of key 20 in Z26 is 6, while the multiplicative inverse of key 15 in Z26 is 7. Now, the decryption is performed as shown here:

18. Encrypt the plaintext message ‘ATTACK SUCCESSFUL’ by using the initial key stream as 12 with the autokey cipher.
Ans.: The plaintext will be encrypted to form the ciphertext as shown here:
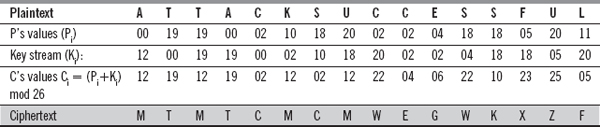
Hence, the corresponding ciphertext is ‘MTMTCMCMWEGWKXZF’.
19. Given the key ‘MONARCHY', apply the Playfair cipher to the plaintext ‘FACTIONALISM’. Decrypt the ciphertext also.
Ans.: The given keyword = ‘MONARCHY’
The corresponding keyword matrix is as follows:
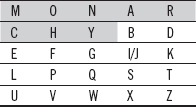
Encryption
The given plaintext is ‘FACTIONALISM’. The different pairs of plaintext are FA, CT, IO, NA, LI and SM. These pairs are encrypted as follows:
 In the first pair, the letter F is at position (3, 2), and A is at position (1, 4) in the keyword matrix. That is, neither their rows nor their columns match. Thus, F is replaced with the letter at the intersecting position of the third row and fourth column, which is either I or J. Let us use I. Similarly, A is replaced with the letter at the intersecting position of the first row and second column, which is the letter O.
In the first pair, the letter F is at position (3, 2), and A is at position (1, 4) in the keyword matrix. That is, neither their rows nor their columns match. Thus, F is replaced with the letter at the intersecting position of the third row and fourth column, which is either I or J. Let us use I. Similarly, A is replaced with the letter at the intersecting position of the first row and second column, which is the letter O.
 For the next two pairs, CT and IO, neither the rows nor the columns match. Thus, using the same rule as earlier, they are replaced with DL and FA, respectively.
For the next two pairs, CT and IO, neither the rows nor the columns match. Thus, using the same rule as earlier, they are replaced with DL and FA, respectively.
 In the fourth pair, NA, both letters appear in the same row. Thus, they are replaced with the letters at their immediate right positions, which are A and R.
In the fourth pair, NA, both letters appear in the same row. Thus, they are replaced with the letters at their immediate right positions, which are A and R.
 In the last two pairs, LI and SM, neither the rows nor the columns match. Thus, they are replaced with SE and LA, respectively.
In the last two pairs, LI and SM, neither the rows nor the columns match. Thus, they are replaced with SE and LA, respectively.
Hence, the corresponding ciphertext is ‘IODLFAARSELA’.
Decryption
The different pairs of ciphertext are IO, DL, FA, AR, SE and LA. These pairs are decrypted as follows:
 In the first pair, the letter I is at position (3, 4) and O appears at position (1, 2) in the keyword matrix. That is, neither their rows nor their columns match. Thus, I is replaced with the letter at the intersecting position of third row and second column, which is F. Similarly, O is replaced with the letter at the intersecting position of first row and fourth column, which is the letter A.
In the first pair, the letter I is at position (3, 4) and O appears at position (1, 2) in the keyword matrix. That is, neither their rows nor their columns match. Thus, I is replaced with the letter at the intersecting position of third row and second column, which is F. Similarly, O is replaced with the letter at the intersecting position of first row and fourth column, which is the letter A.
 For the next two pairs, DL and FA, neither the rows nor the columns match. Thus, using the same rule as earlier, they are replaced with CT and IO, respectively.
For the next two pairs, DL and FA, neither the rows nor the columns match. Thus, using the same rule as earlier, they are replaced with CT and IO, respectively.
 In the fourth pair, AR, both letters appear in the same row. Thus, they are replaced with letters at their immediate left positions, which are N and A.
In the fourth pair, AR, both letters appear in the same row. Thus, they are replaced with letters at their immediate left positions, which are N and A.
 In the last two pairs, SE and LA, neither the rows nor the columns match. Thus, they are replaced with LI and SM, respectively.
In the last two pairs, SE and LA, neither the rows nor the columns match. Thus, they are replaced with LI and SM, respectively.
Hence, the corresponding plaintext is ‘FACTIONALISM’.
20. Encrypt the plaintext message ‘honesty is the best’ by using a 6-character key ‘CENTRE’ with the Vigenere cipher.
Ans.: The encryption process using the Vigenere cipher is shown here:

Hence, the corresponding ciphertext is ‘jsaxjxamfmyidifm’.
21. Given the key ‘GYBNQKURP', apply the Hill cipher to the plaintext ‘ACT’ to show how encryption and decryption are performed and prove authenticity.
Ans.: The given plaintext (P) = ‘ACT’
Key (K) = ‘GYBNQKURP’
The key used can be written as:
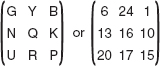
Encryption
The plaintext ACT can be written as:
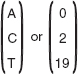
Thus, the ciphertext (is) C given as PK mod 26 as shown here.
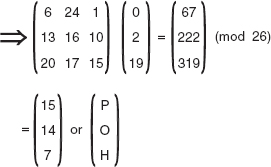
Hence, the corresponding ciphertext is ‘POH’.
Decryption
In order to decrypt the ciphertext, we first need to calculate the inverse of the key matrix and then multiply it with the ciphertext, that is, P = K-1C mod 26. Now, the inverse of the key matrix is:
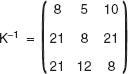
Thus, the plaintext can be obtained as shown here:
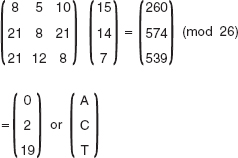
Since the receiver receives the same message as sent by the sender, the authenticity of the message is proved.
22. Generate the ciphertext message using the one-time pad algorithm for the plaintext message ‘higautam’.
Ans.:
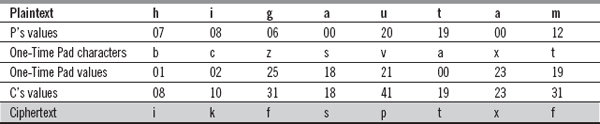
Hence, the corresponding ciphertext is ‘ikfsptxf’.
Multiple-choice Questions
1. Which of the following is a monoalphabetic cipher?
(a) Caesar cipher
(b) Autokey cipher
(c) Vigenere cipher
(d) All of these
2. The __________ cipher is a combination of additive and multiplicative ciphers with a pair of keys.
(a) Affine
(b) Caesar
(c) Autokey
(d) Shift
3. In the polyalphabetic cipher, the characters in plaintext have a __________ relationship with the characters in ciphertext.
(a) One-to-one
(b) One-to-many
(c) Many-to-one
(d) Many-to-many
4. The Hill cipher belongs to the category of ciphers, named __________.
(a) Stream cipher
(b) Block cipher
(c) Both (a) and (b)
(d) None of these
5. The __________ cipher can be categorized as a stream cipher.
(a) Additive
(b) Hill
(c) Playfair
(d) None of these
6. Which of the following is/are components of a modern block cipher?
(a) Circular shift
(b) S-box
(c) P-box
(d) All of these
7. __________ is based on the idea of hiding the relationship between the ciphertext and the key.
(a) Diffusion
(b) Confusion
(c) Both (a) and (b)
(d) None of these
8. The concept of product cipher was proposed by __________.
(a) Verman
(b) Fiestel
(c) Lester S. Hill
(d) Shannon
9. The Feistel cipher uses the __________ operation.
(a) AND
(b) NOR
(c) XOR
(d) OR
10. A non-Feistel cipher uses only the __________ P-box.
(a) Compression
(b) Expansion
(c) Straight
(d) None of these
Answers
1. (a)
2. (a)
3. (b)
4. (b)
5. (a)
6. (d)
7. (b)
8. (d)
9. (c)
10. (c)
1. Explain DES with its structure. Also explain its function.
Ans.: Data Encryption Standard (DES) is a symmetric-key block cipher that was first published in 1977 by National Institute of Standards and Technology (NIST). It was originally proposed by IBM in 1973 in response to the request for proposals for a national symmetric-key cryptosystem. This encryption standard was adopted by the US government for non-classified information and by various industries for use in security products. DES is also known as the Data Encryption Algorithm (DEA) by ANSI and DEA-1 by ISO.
At the sender's end, DES divides the plaintext into 64-bit blocks and encrypts each block using a 56-bit cipher key to produce a 64-bit ciphertext block. At the receiver's end, the reverse process is followed; that is, DES decrypts the 64-bit ciphertext to obtain 64-bit plaintext. Being a symmetric-key cipher, DES uses the same 56-bit cipher key for both encryption and decryption. Originally, the cipher key is of 64 bits including 8 parity bits; however, the usable bits in key are only 56.
DES involves multiple rounds to produce ciphertext, and the key used in each round (called the round key) is the subset of the general key, called the cipher key; the round keys are generated by the round key generator. Thus, if there are P rounds in the cipher, then the round key generator produces total P round keys (K1, K2,…, KP) where K1 is used in first round, K2 in second round and so on.
DES Structure
Figure 4.1 shows the general structure of the DES encryption algorithm (referred to as the DES cipher); the design of the DES decryption algorithm (referred to as the DES reverse cipher) is also similar, except that the round keys are used in the reverse order from that of encryption. The whole process of producing ciphertext from plaintext comprises 19 stages. The first stage is the initial transposition, which performs keyless straight permutations that are the inverse of each other on the 64-bit plaintext block, according to a predetermined rule. The next 16 stages are the rounds that are functionally similar and, in each round, a different round key Ki of 48 bits derived from the cipher key of 56 bits is used. The second-last stage performs a swap function in which the leftmost 32 bits are exchanged with the rightmost 32 bits. The last stage, final transposition, is simply the opposite of the first stage; that is, it performs inverse transposition on the 64 bits received from the 32-bit swapper to generate
a 64-bit ciphertext block. For example, if in the initial transposition stage, the input bit 2 becomes the output bit 50, then in the final transposition stage, the input bit 50 becomes the output bit 2. At the receiver's end, the decryption is performed using the same key as in encryption; however, the steps are performed in the reverse order.
The structure of one of the 16 rounds (say, i-th round) during encryption in DES is shown in Figure 4.2. It takes two inputs: the leftmost 32 bits as left input (Li) and the rightmost 32 bits as right input (Ri), and produces two outputs, left output (Li+1) and right output (Ri+1), each of 32 bits. The left output (Li+1) is just the right input (Ri). The right output (Ri+1) is obtained by first applying the DES function (f) on the right input (Ri) and the 48-bit key (Ki) being used in the i-th round, denoted as f(Ri, Ki), and then performing the bitwise XOR of the result of DES function and the left input (Li). The structure of decryption round in DES is simply the opposite of the encryption round.
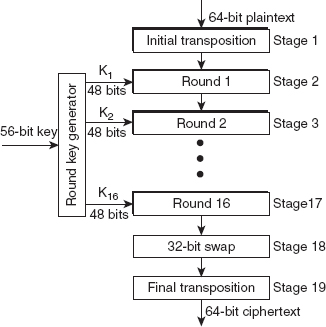
Figure 4.1 General Structure of DES Encryption
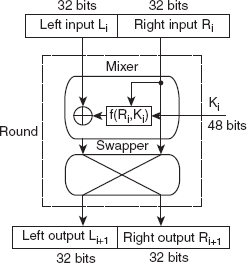
Figure 4.2 Structure of Encryption Round
DES Function
The essence of DES is the DES function, f(Ri, Ki). During each round, this function takes the -rightmost 32 bits and applies the 48-bit round key generated for that round on it to produce the 32-bit output. The function comprises four steps (see Figure 4.3), which are described as follows:
1. Expansion P-box: The right output (Ri) of 32 bits is initially fed into the expansion P-box, which expands it to 48 bits, because the key (Ki) used is of 48 bits. For this, the 32 bits of Ri are divided into eight blocks of 4 bits each. Each 4-bit block is then expanded to 6 bits using a predetermined rule, as explained in the following text.
a. Copy the input bits 1, 2, 3 and 4 to output bits 2, 3, 4 and 5, respectively.
b. Copy the input bit 4 of the previous block to output bit 1 of the block under consideration. This step is an exception to the first block.
c. Copy the input bit 1 of the next block to output bit 6 of the block under consideration. This step is an exception to the last (eighth) block.
Notice that in case of first block, the input bit 4 of the last block becomes the output bit 1, while in case of last block, the input bit 1 of the first block becomes the output bit 6. The resulting 48 bits are forwarded to the next step.
2. XOR operation: A bitwise XOR operation is performed on the 48-bit output obtained from the previous step and 48-bit round key Ki, resulting in 48 bits. These 48 bits are forwarded to the next step.
3. S-boxes: The 48-bit output obtained after the XOR operation is broken down into eight groups, with each group consisting of 6 bits. Each group of 6 bits is then fed to one of eight S-boxes. Each S-box follows a predetermined rule to map six inputs to four outputs and, thus, total 32 bits are obtained from eight S-boxes. The rule for substitution in each S-box is based on a table consisting of four rows and 16 columns. To perform the substitution in an S-box, the input bits 1 and 6 (2 bits) together define the row number, and the input bits 2, 3, 4 and 5 (4 bits) together define the column number. Now, the value at the intersection of the computed row and column number defines the 4 output bits. For example, if the input to an S-box is 101011, then the row number is 11 (equivalent to decimal number 3), and the column number is 0101 (equivalent to decimal number 5). Now, if the value at the intersection of third row and fifth column is 6, then the resulting output bits will be 0110.
4. Straight P-box: The 32 bits obtained from S-boxes are input to a straight P-box, which permutes them and produces 32 bits as output. As with the previous operations, the input bits are permuted based on the predetermined rule. For example, the input bit 7 becomes the output bit 2.
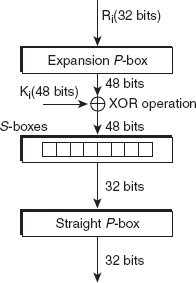
Figure 4.3 DES Function
2. Explain key generation of DES with the help of a block diagram.
Ans.: The generation of keys in DES for each round is done by round-key generator. The round-key generator produces sixteen 48-bit keys out of a 56-bit cipher key, one for each round. As in DES, the original key size is 64 bits, including the parity bits; therefore, the parity bits are initially dropped using the parity bit drop process before the actual key generation process starts. The parity bit drop process is actually a compression transposition step that drops the parity bits present at every eighth position (8, 16, 24, 32, 40, 48, 56 and 64) in the 64-bit key, generating a 56-bit key. Then the 56 bits of the key are permuted according to a predetermined rule, as shown in Table 4.1. For example, the bit 1 of the original 56-bit key becomes the eighth bit of the new 56-bit key. This 56-bit key is the actual cipher key used for key generation.
Table 4.1 Parity Drop Box Table
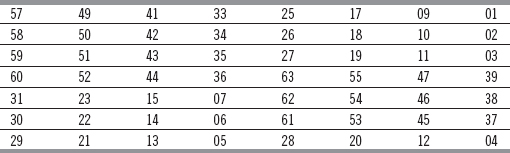
During each round, the round key generator uses the 56-bit cipher key and performs the following steps to generate the key for that round (see Figure 4.4).
1. Divide the plaintext into two halves of 28 bits each.
2. Perform circular left shift operation on each 28-bit half. Shifting is done either by 1 or 2 bits, depending on the round number. In case of rounds 1, 2, 9 and 16, shifting is done by 1 bit, while in the case of the other rounds, shifting is done by 2 bits.
3. After shifting has been performed, both halves are combined again to form a 56-bit part. These 56 bits are then given as input to the compression P-box.
4. The compression P-box, as its name suggests, compresses the 56-bit input to produce 48-bit output. This 48-bit output generated from the P-box is then used as a key for the round.
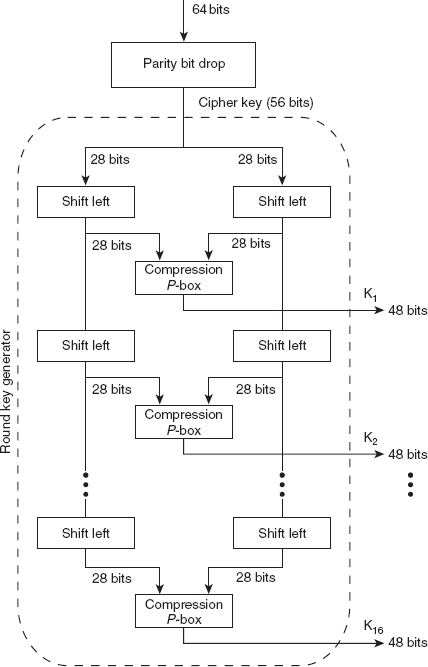
Figure 4.4 Key Generation in DES
3. Discuss the strength of DES.
Ans.: The strength of any cryptographic system is measured by the fact that how resistive it is to an attack. In case of DES, the strength of the system lies in two important aspects: key size and the use of S-boxes.
 Key size: DES uses 56-bit keys in each round, which means 256 (approximately 7.2 * 1016) number of keys. Therefore, a brute-force attack on DES seems practically impossible. However, if we assume that, to get the correct key, only half of the total keys are needed to be examined, a single computer performing one DES encryption per microsecond would still take more than 1000 years to break the DES.
Key size: DES uses 56-bit keys in each round, which means 256 (approximately 7.2 * 1016) number of keys. Therefore, a brute-force attack on DES seems practically impossible. However, if we assume that, to get the correct key, only half of the total keys are needed to be examined, a single computer performing one DES encryption per microsecond would still take more than 1000 years to break the DES.
 Use of S-boxes: DES uses eight S-boxes (substitution tables) in each round. The internal design of these substitution tables has been kept secret by IBM. Therefore, a suspicion has grown that there may be some weaknesses in the internal design of S-boxes that can be exploited by cryptanalysts to break the DES security. Over the years, a number of studies have appeared which suggest that there is a scope of attacking DES through S-boxes; however, no one has succeeded till date.
Use of S-boxes: DES uses eight S-boxes (substitution tables) in each round. The internal design of these substitution tables has been kept secret by IBM. Therefore, a suspicion has grown that there may be some weaknesses in the internal design of S-boxes that can be exploited by cryptanalysts to break the DES security. Over the years, a number of studies have appeared which suggest that there is a scope of attacking DES through S-boxes; however, no one has succeeded till date.
4. Comment on the weaknesses of DES.
Ans.: Although the DES cipher is widely used and is resistant to various attacks, some weaknesses are still found in it. The weaknesses have been found in two aspects of DES, in the cipher design and in the cipher key.
Weakness in the Cipher Design
The DES cipher involves a number of S-boxes and P-boxes, which suffer from certain problems. Some weaknesses found in S-boxes are as follows:
 In fourth S-box, the last 3 bits in the output can be obtained in the same way as the first bit in the output by performing complement operation on some of the bits in input.
In fourth S-box, the last 3 bits in the output can be obtained in the same way as the first bit in the output by performing complement operation on some of the bits in input.
 In a single round, the same output can be obtained if the bits in only three neighbouring S-boxes are changed.
In a single round, the same output can be obtained if the bits in only three neighbouring S-boxes are changed.
 Two specific chosen inputs when given to the array of eight S-boxes can result in the same output.
Two specific chosen inputs when given to the array of eight S-boxes can result in the same output.
Some weaknesses found in P-boxes are as follows:
 The initial and final permutation stages used in DES do not provide any security benefits.
The initial and final permutation stages used in DES do not provide any security benefits.
 In the expansion permutation used within the DES function, the input bits 1 and 4 of each 4-bit series are repeated in the output.
In the expansion permutation used within the DES function, the input bits 1 and 4 of each 4-bit series are repeated in the output.
Weakness in the Cipher Key
The cipher key used in DES has got certain shortcomings, which are described as follows:
 Size of cipher key: As the cipher key used in DES is of 56 bits, an intruder needs to examine 256 possible keys in order to attempt a brute-force attack. If a computer with a single processor that can process about one million keys per second is used for examining the whole key domain, it will take more than 2000 years to attempt brute-force attack on DES. In 1977, this period of 2000 years reduced to 120 days when 3500 networked computers and the concept of parallel processing were used. The entire key domain was divided into several parts, and each computer had to examine only some parts. Furthermore, a secret society having 42000 members can break the
cipher and thus, determine the key in 10 days only. Thus, it can be concluded that the DES with a cipher key of 56 bits is not safe enough for use.
Size of cipher key: As the cipher key used in DES is of 56 bits, an intruder needs to examine 256 possible keys in order to attempt a brute-force attack. If a computer with a single processor that can process about one million keys per second is used for examining the whole key domain, it will take more than 2000 years to attempt brute-force attack on DES. In 1977, this period of 2000 years reduced to 120 days when 3500 networked computers and the concept of parallel processing were used. The entire key domain was divided into several parts, and each computer had to examine only some parts. Furthermore, a secret society having 42000 members can break the
cipher and thus, determine the key in 10 days only. Thus, it can be concluded that the DES with a cipher key of 56 bits is not safe enough for use.
 Weak keys: Out of 256 keys, there are four keys that comprise either all 0s, all 1s or half 0s and half 1s. These four keys are referred to as the weak keys. When the round keys are created from any of the weak keys, they follow the same pattern as that of the cipher key. For example, a round key created from the weak key containing all 0s or all 1s will also comprise all 0s or 1s, respectively. This is because the cipher key is divided into two equal parts during key generation in DES. Thus, neither substitution nor permutation affects the block containing all 1s or all 0s. The disadvantage of using a weak key lies in the fact that it is the inverse of itself. That is, when a plaintext block is encrypted with a weak key and then the result is further encrypted with the same weak key, we get back the original plaintext block. Exploiting this fact, the intruder can easily attempt to decrypt the intercepted ciphertext using the weak keys. In case the result is the same after two decryptions, it means the intruder has got the key. Therefore, it is recommended that the use of weak keys be avoided.
Weak keys: Out of 256 keys, there are four keys that comprise either all 0s, all 1s or half 0s and half 1s. These four keys are referred to as the weak keys. When the round keys are created from any of the weak keys, they follow the same pattern as that of the cipher key. For example, a round key created from the weak key containing all 0s or all 1s will also comprise all 0s or 1s, respectively. This is because the cipher key is divided into two equal parts during key generation in DES. Thus, neither substitution nor permutation affects the block containing all 1s or all 0s. The disadvantage of using a weak key lies in the fact that it is the inverse of itself. That is, when a plaintext block is encrypted with a weak key and then the result is further encrypted with the same weak key, we get back the original plaintext block. Exploiting this fact, the intruder can easily attempt to decrypt the intercepted ciphertext using the weak keys. In case the result is the same after two decryptions, it means the intruder has got the key. Therefore, it is recommended that the use of weak keys be avoided.
 Semi-weak keys: In 256 keys, there are six pairs of keys that create only two distinct round keys for total 16 rounds, and each key is used in eight rounds. These six key pairs are referred to as semi-weak keys. Each pair of semi-weak keys creates the same two round keys; however, they are used in 16 rounds in different order.
Semi-weak keys: In 256 keys, there are six pairs of keys that create only two distinct round keys for total 16 rounds, and each key is used in eight rounds. These six key pairs are referred to as semi-weak keys. Each pair of semi-weak keys creates the same two round keys; however, they are used in 16 rounds in different order.
 Possible weak keys: There are 48 such keys that create only four different round keys, and each of them is repeated four times. These 48 keys are referred to as possible weak keys.
Possible weak keys: There are 48 such keys that create only four different round keys, and each of them is repeated four times. These 48 keys are referred to as possible weak keys.
 Key complement: In 256 keys, half of the keys (that is, 255) are the complement of the other half keys. That is, if half of the total keys are known, the remaining half can be obtained by simply inverting the bits (1 to 0 or 0 to 1) of the known keys. This proves to be beneficial to the intruder as now he or she has to examine only half of the key domain to attempt a brute-force attack. This is because of the fact that if the complement of plaintext is encrypted using the complement of a key, then a complement of the ciphertext is obtained.
Key complement: In 256 keys, half of the keys (that is, 255) are the complement of the other half keys. That is, if half of the total keys are known, the remaining half can be obtained by simply inverting the bits (1 to 0 or 0 to 1) of the known keys. This proves to be beneficial to the intruder as now he or she has to examine only half of the key domain to attempt a brute-force attack. This is because of the fact that if the complement of plaintext is encrypted using the complement of a key, then a complement of the ciphertext is obtained.
 Key clustering: The situation where two or more different keys result in the same ciphertext from the same plaintext is referred to as key clustering. In DES, each pair of semi-weak keys is a key cluster.
Key clustering: The situation where two or more different keys result in the same ciphertext from the same plaintext is referred to as key clustering. In DES, each pair of semi-weak keys is a key cluster.
5. What do you understand by differential and linear cryptanalysis of DES?
Ans.: Differential cryptanalysis is a chosen-plaintext attack that was introduced by Eli Biham and Adi Shamir in 1990. The basic idea of this attack is to choose a pair of plaintexts having specific differences and then analysing the corresponding ciphertext pair. The attacker examines how these differences propagate in the ciphertexts as the plaintexts pass through the rounds of DES. Using the differences in the ciphertexts, the attacker determines the probability of different possible keys and, eventually, as ciphertexts are analysed progressively, the actual cipher key emerges. The designers of DES were aware of chosen-plaintext attacks; therefore, they used S-boxes and 16 rounds to encrypt the plaintext in DES. Doing so makes DES invulnerable to differential cryptanalysis as breaking a DES message by differential analysis will need either 247 chosen plaintexts or 255 known plaintexts. Although differential cryptanalysis attacks are much powerful than brute-force attacks, finding 247 chosen plaintexts or 255 known plaintexts is not practically possible. Moreover, if we increase the number of rounds in DES to 20, then a differential cryptanalysis attack needs 264 chosen plaintexts, which is practically impossible, because DES can only have 264 possible plaintexts.
Linear cryptanalysis is a cryptanalysis technique that was introduced by Mitsuru Matsui in 1993. It is a known-plaintext attack that is based on linear approximations. The idea is to perform the XOR operation on some bits in the plaintext and ciphertext together, and then take the XOR of the result; the final result is a single bit that will be the XOR of some bits in the key. The linear cryptanalysis attacks on DES are more vulnerable than differential cryptanalysis attacks, because the designers of DES had no idea about linear cryptanalysis attacks at the time of designing. Also, S-boxes are not very resistant to linear cryptanalysis. A linear cryptanalysis attack can break DES in 243 pairs of known plaintexts. However, it is not practically feasible to find so many pairs.
6. Define Avalanche effect and completeness effect. Also, discuss the strength of DES with regard to these.
Ans.: Both Avalanche effect and completeness are the desirable properties of a block cipher. These properties are described as follows:
 Avalanche effect: This property states that any small change made to the plaintext or the key should cause a significant change in the ciphertext. That is, change in a single bit in the plaintext should result in changes in multiple bits in the ciphertext. This property is desired because the lack of it would considerably reduce the key domain to be searched, thus making it easier for a cryptanalyst to attempt a brute-force attack. In general, an encryption method is considered to have a good avalanche effect if change in a single bit of plaintext results in a random change in approximately half of the bits in the ciphertext.
Avalanche effect: This property states that any small change made to the plaintext or the key should cause a significant change in the ciphertext. That is, change in a single bit in the plaintext should result in changes in multiple bits in the ciphertext. This property is desired because the lack of it would considerably reduce the key domain to be searched, thus making it easier for a cryptanalyst to attempt a brute-force attack. In general, an encryption method is considered to have a good avalanche effect if change in a single bit of plaintext results in a random change in approximately half of the bits in the ciphertext.
DES has been proved to be very strong with regard to the Avalanche effect. In DES, when two plaintext blocks having only a single bit difference are encrypted using the same key, the ciphertexts obtained do not have much resemblance. Similarly, when the same plaintext is encrypted using two neighbouring keys (keys with only a small difference), we obtain two significantly different ciphertexts.
 Completeness effect: This property states that each bit of the ciphertext should depend on -multiple bits of the plaintext or the key. It tightens the concept of avalanche effect even more by requiring that, for each modified bit in the plaintext or the key, the change in ciphertext must be distributed uniformly. In other words, completeness means that the avalanche effect spans across all pairs of bits in the plaintext and ciphertext, almost uniformly. DES represents a strong completeness effect because of the diffusion and confusion produced by the P-boxes and S-boxes used in the DES cipher.
Completeness effect: This property states that each bit of the ciphertext should depend on -multiple bits of the plaintext or the key. It tightens the concept of avalanche effect even more by requiring that, for each modified bit in the plaintext or the key, the change in ciphertext must be distributed uniformly. In other words, completeness means that the avalanche effect spans across all pairs of bits in the plaintext and ciphertext, almost uniformly. DES represents a strong completeness effect because of the diffusion and confusion produced by the P-boxes and S-boxes used in the DES cipher.
7. What is double DES? Explain the meet-in-the-middle attack.
Ans.: Double DES (2-DES) is the simplest version of multiple-DES. As the name implies, double DES performs DES encryption/decryption twice using two different keys (K1 and K2) of 56 bits each. This increases the key size to 112 bits, thus, increasing the cryptographic strength to double that of normal DES.
At the sender's end, the plaintext P is initially encrypted using DES with key K1 to obtain the temporary ciphertext T = EK1(P). Then, the temporary ciphertext T is again encrypted using DES with key K2 to obtain the final ciphertext C = EK2(T), that is, C = EK2(EK1(P)). At the receiver's end, the reverse process is followed to decrypt the ciphertext, and the keys are used in the reverse order of that of encryption. That is, first the ciphertext C is decrypted using DES with key K2 to obtain the temporary plaintext T′ = DK2(C), and then the temporary plaintext T′ is again decrypted using DES with key K1 to get back the original plaintext P = DK1(T′), that is, P = DK1(DK2(C)). Figure 4.5 shows the encryption and decryption processes in double DES.
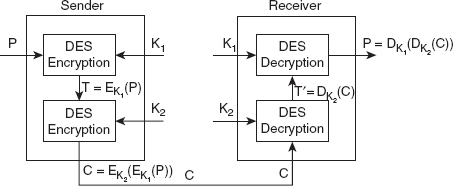
Figure 4.5 Encryption and Decryption in Double DES
Meet-in-the-middle Attack
The use of key size of 112 bits implies that an attacker would need 2112 attempts, which is twice that of normal DES, to break the cipher key. However, this is not true because of the meet-in-the-middle attack that was introduced by Merkle and Hellman. In this attack, encryption is performed from one end, decryption is performed from the other and matching the result in the middle, and it is hence that the attack is named so.
The meet-in-the-middle attack is based on the observation that if we have C = EK2(EK1(P)), then we can have EK1(P)= DK2(C), that is, T = T′. To understand how this attack happens, let us consider that the attacker knows a plaintext block P and a ciphertext block C of some message. Now, to determine K1 and K2, the attacker may perform the following steps:
1. For each of the 256 possible values of K1, allocate a large table in the memory and perform the following:
a. Compute the temporary ciphertext T = EK1(P).
b. Store the value of T in the next available row of the table in memory.
After performing the preceding two steps, we get a table containing the values of the temporary ciphertext T.
2. For each of the 256 possible values of K2, perform the following:
a. Compute the temporary plaintext T′ = DK2(C).
b. Compare the value of T′ with all the values in the table of temporary ciphertext T.
c. If T′ matches with any value of T in the table, use the corresponding pair of K1 and K2 to encrypt and decrypt another known pair of plaintext (say, P′) and ciphertext (say, C′) blocks, respectively.
d. If EK1(P′)= DK2(C′), then K1 and K2 are the correct keys and can be used for remaining blocks of the message.
Though the meet-in-the-middle attack is possible on double-DES, it needs a lot of memory space to store the values of T. For example, if a 64-bit plaintext block and a 56-bit key are used, then 256 64-bit blocks (equivalent to 217 bytes) of memory would be needed, which is too high. This makes the meet-in-the-middle attack practically infeasible.
8. Write a short note on triple DES.
Ans.: To overcome the problem of meet-in-the-middle attack in double DES, triple DES (3-DES) was developed. As the name implies, it performs the DES encryption process thrice. There are two implementations of 3-DES: one with two keys, and another with three keys.
3-DES with Two Keys
This version uses two keys, say K1 and K2 of 56 bits each to perform encryption and decryption. At the sender's end, the following three steps are performed to produce ciphertext C from the plaintext P.
1. Encrypt the plaintext P using DES with key K1 to produce T = EK1(P).
2. Decrypt T using DES with key K2 to produce S = DK2(EK1(P)).
3. Encrypt S using DES with key K1 to produce ciphertext C = EK1(DK2(EK1(P))).
Similarly, during decryption, the following three steps are used to obtain plaintext P from ciphertext C.
1. Decrypt the ciphertext C using DES with key K1 to produce T′ = DK1(C).
2. Encrypt T′ using DES with key K2 to produce S′ = EK2(DK1(C)).
3. Decrypt S′ using DES with key K1 to get back the original plaintext P = DK1(EK2(DK1(C))).
The use of two keys in 3-DES increases the key size to 112 bits and provides more secure communication. In addition, there is no special significance of using decryption in the second step. It is simply used to provide backward compatibility with the original DES by putting K1 = K2. In case of K1 = K2, 3-DES becomes equivalent to single DES and, thus, enables the users of 3-DES to decrypt the data encrypted by the users of single DES.
3-DES with Three Keys
This version uses three keys of 56 bits each, and a different key is used for performing encryption/decryption in each step. At the sender's end, the plaintext P is encrypted to form ciphertext C, as shown here:
c = EK3(DK2(EK1(P)))
At the receiver's end, the keys are used in the reverse order from that of encryption to obtain the original plaintext P from the ciphertext C, as shown here:
P = DK1(EK2(DK3(C)))
The use of three different keys increases the key length to 168 bits, making 3-DES three-key version more secure; however, it results in an increased overhead due to managing and transporting one more key. Here, the backward compatibility with DES is provided by having either K1 = K2 or K2 = K3.
9. Explain IDEA encryption and decryption in brief.
Ans.: The International Data Encryption Algorithm (IDEA) is a patented and universally applicable block cryptographic algorithm. It was proposed and launched in 1990 by Xuejia and James, and was initially named as Proposed Encryption Standard (PES). In 1991, some improvements were made in PES, and the new improved version was given the name Improved PES (IPES). Then, it was renamed to IDEA in 1992.
IDEA is a block cipher and is considered one of the strongest cryptographic algorithms. It offers effective protection of stored and transmitted data against unauthorized access by third parties. It uses a 128-bit-long key and both diffusion and confusion for encryption. This makes it more secure than the widely known DES, which is based on the use of a 56-bit key. However, as with DES, IDEA also operates on 64-bit plaintext blocks, and uses the same algorithm for encryption and decryption.
Though IDEA is powerful and strong, it is not as popular as DES because of two reasons. Firstly, it is not free and must be licensed before being used for commercial purposes. Secondly, IDEA keeps only a few history and track records as compared to DES. However, one popular e-mail privacy technique called Pretty Good Privacy (PGP) is based on IDEA.
Working of IDEA
Figure 4.6 shows the broad-level steps involved in the IDEA encryption process. The IDEA algorithm breaks down the 64-bit input data block into four 16-bits data blocks: P1, P2, P3 and P4. These four data blocks are then processed through eight rounds, and each round uses six 16-bit sub-keys generated from the original key. During each round, these data blocks are transformed by applying various arithmetic operations among each other and with the sub-keys. The whole encryption process uses a total of 52 sub-keys (K1 to K52), out of which six sub-keys, K1 to K6, are used in the first round. In the second round, the next six sub-keys, K7 to K12, are used and so on. Finally, the sub-keys K43 to K48 are used in the eighth round. The final step of the encryption process is output transformation, which uses four sub-keys, K49 to K52. The output produced from this step is four blocks of ciphertext: C1, C2, C3 and C4, each of 16 bits, which are then concatenated to form the final 64-bit ciphertext block.
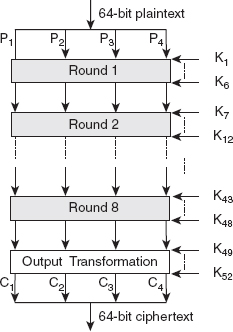
Figure 4.6 IDEA Encryption Process
Encryption Round
Each round of the IDEA encryption process performs a sequence of operations on four plaintext blocks using the corresponding six sub-keys. These operations include XOR, addition and multiplication. It may be noted that addition and multiplication operations here do not imply the ordinary addition and multiplication; rather, they are addition modulo 216 and multiplication modulo (216+1), respectively. The steps involved in an encryption round are as follows:
1. Multiply P1 and K1.
2. Add P2 and K2.
3. Add P3 and K3.
4. Multiply P4 and K4.
5. XOR the results of step 1 and step 3.
6. XOR the results of step 2 and step 4.
7. Multiply the results of step 5 with K5.
8. Add the results of steps 6 and 7.
9. Multiply the results of step 8 with the K6.
10. Add the results of step 7 and step 9.
11. XOR the results of step 1 and step 9 and store the result in R1.
12. XOR the results of step 3 and step 9 and store the result in R2.
13. XOR the results of step 2 and step 10 and store the result in R3.
14. XOR the results of step 4 and step 10 and store the result in R4.
15. Swap the blocks R2 and R3.
The resultant data blocks R1, R2, R3 and R4 in each round are passed to the next round. Note that the eighth round does not involve the last step (step 15); that is, it does not perform the swapping of blocks R2 and R3. After performing all the eight rounds, the final data blocks, R1, R2, R3 and R4, of 16 bits each are passed to the next stage – that is, output transformation.
Output Transformation
This stage applies four keys, K49 to K52, on the input data blocks, R1, R2, R3 and R4, and produces the four ciphertext blocks, C1, C2, C3 and C4, by performing the following steps:
1. Multiply R1 and K49 to obtain C1.
2. Multiply R2 and K50 to obtain C2.
3. Multiply R3 and K51 to obtain C3.
4. Multiply R4 and K52 to obtain C4.
Finally, the four ciphertext blocks (C1, C2, C3 and C4) are combined to form a 64-bit ciphertext block.
Decryption
The decryption process of IDEA is the same as that of the encryption process; however, the sub-keys are used in the reverse order from that of encryption. The sub-keys used for decryption are the inverse of the sub-keys used for encryption.
Strength of IDEA
The IDEA algorithm is resistant to all known cryptanalysis attacks. It uses a 128-bit-long key. Therefore, to attempt a cryptanalysis attack on IDEA, the attacker needs to perform 2128 encryption operations, which is practically infeasible.
10. Explain the sub-key generation in the IDEA algorithm.
Ans.: As each round in the IDEA algorithm uses six sub-keys of 16-bit each and the output transformation step also needs four sub-keys, thus, a total of 52 16-bit sub-keys are required from the key length of 128 bits. For this, a sub-key generation process is used, which generates the sub-keys as follows:
 In the first round, six sub-keys of 16 bits each, that is, 96 bits, are required. Therefore, the first 96 bits of 128-bit key (say,
In the first round, six sub-keys of 16 bits each, that is, 96 bits, are required. Therefore, the first 96 bits of 128-bit key (say, K) are used for the first round. The rest of the key bits (97–128) remain unused and, thus, are kept for the second round.
 The second round also requires six sub-keys of 16 bits each; that is, a total of 96 bits. However, we have only 32 unused bits of the key
The second round also requires six sub-keys of 16 bits each; that is, a total of 96 bits. However, we have only 32 unused bits of the key K and, therefore, we need 64 bits more. To generate the rest of the bits, the IDEA algorithm uses the key shifting technique. In this technique, the original 128-bit key K is shifted left circularly by 25 bits. After shifting, the 26-th bit of the original key K becomes the first bit of the new key (say, K′), and the 25-th bit of key K becomes the 128-th bit of key K′. Now, the bits 1 to 64 of key K′ and the unused 32 bits (97–128) of key K are used to form six 16-bit sub-keys for the second round.
 In the third round, we have 64 unused bits of key
In the third round, we have 64 unused bits of key K′ generated in the second round, and 32 bits are still required. Thus, the key shifting technique is again applied, and the key K′ is left shifted by 25 bits. This process continues to obtain 96 bits in each round.
 The output transformation stage also needs four sub-keys of 16 bits each. Notice that after the eighth round, the key gets exhausted. Thus, the key is left shifted by 25 bits, and the bits 1 to 64 of the newly created key are used to generate four sub-keys (
The output transformation stage also needs four sub-keys of 16 bits each. Notice that after the eighth round, the key gets exhausted. Thus, the key is left shifted by 25 bits, and the bits 1 to 64 of the newly created key are used to generate four sub-keys (K49 to K52) for this stage.
11. Explain Advanced Encryption Standard.
Ans.: The Advanced Encryption Standard (AES) is the latest and, potentially, the most secure encryption method published by NIST. It is a symmetric-key block cipher that was designed to be a significant improvement over DES/3-DES. In 1990s, the US government decided to standardize the cryptographic algorithm and to name it as AES. In response to this, a lot of proposals were submitted. After long debates, in 2000, the US government chose one of the proposals, the Rijndael algorithm, as AES. This algorithm is named on the surnames of the two Belgian researchers Vincent Rijmen and John Daemen. Finally, in 2001, AES was published as Federal Information Processing Standard (FIPS) 197 by NIST.
General Design of AES
AES is a non-Feistel cipher that operates on a data block of 128 bits (16 bytes) and comprises several rounds for encryption and decryption. It is available in three versions, depending on the key size and the number of rounds used. These versions include AES-128 with key size 128 bits and 10 rounds, AES-192 with key size 192 bits and 12 rounds and AES-256 with key size 256 bits and 14 rounds. Despite the fact that each version uses a different key size, the round keys used in each version are always 128 bits long, which is the same size as that of the plaintext or ciphertext block. In AES, the round keys are generated using the key-expansion algorithm (explained in the next question), and the number of round keys generated is always equal to the number of rounds plus one. Figure 4.7 shows the general design for AES encryption algorithm (referred to as the AES cipher); the design of AES decryption algorithm (referred to as the AES inverse cipher) is also similar, except that the round keys are used in the reverse order from that of encryption.
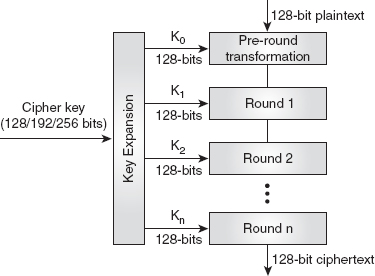
Figure 4.7 General Design of AES Encryption Cipher
Each round in AES consists of many stages, each of which transforms the 16-byte data block. In AES, the term ‘data block’ is used at the beginning and end of the cipher, while before and after each
stage, the term ‘state’ is used to refer to a data block. A state, like a data block, is also 16-bytes long and contains the data before and after the transformation. Usually, a 16-byte state (say, S) is organized as a 4×4 bytes matrix, and each element of the matrix is referred to as Si,j (0≤i≤3 and 0≤j≤3), where i and j denote the row number and column number, respectively.
Structure of Encryption Round
During encryption, each round, excluding the last one, involves four transformations, namely: Substitute Bytes, Shift Rows, Mix Columns and Add Round Key (see Figure 4.8). Each transformation accepts a state, changes it and creates a new state that is given as input to the next transformation or the next round. The last round in AES comprises only three transformations, except the Mix Columns transformation. Moreover, one Add Round Key transformation is applied before the first round (mentioned as pre-round transformation in Figure 4.7). Each transformation in AES is invertible in nature and, during decryption, the inverse of these transformations, namely, Inverse Substitute Bytes, Inverse Shift Rows, Inverse Mix Columns and Add Round Key (which is self-invertible), are used. Figure 4.8 shows the general structure of an encryption round in AES.
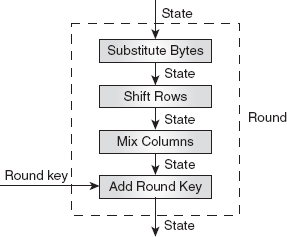
Figure 4.8 General Structure of an Encryption Round
Transformations
All the transformations performed during encryption and decryption fall under four broad categories that include substitution, permutation, mixing and key adding. These transformations are described as follows:
 Substitution: As with DES, AES also performs the substitution of bytes, but using a different mechanism. In AES, substitution is performed for all bytes, and that too, using only one table. This implies that if 2 bytes are the same then their transformations are also same, which is contrastive to DES where eight different S-boxes perform transformations. Moreover, the bytes are substituted either with the help of a transformation table or by performing the mathematical calculations in GF(28) field. The two invertible transformations that fall under this category are as follows:
Substitution: As with DES, AES also performs the substitution of bytes, but using a different mechanism. In AES, substitution is performed for all bytes, and that too, using only one table. This implies that if 2 bytes are the same then their transformations are also same, which is contrastive to DES where eight different S-boxes perform transformations. Moreover, the bytes are substituted either with the help of a transformation table or by performing the mathematical calculations in GF(28) field. The two invertible transformations that fall under this category are as follows:
 Substitute Bytes: It is the first transformation of a round used during encryption. The input to this transformation is a state organized as a 4×4 matrix of bytes. The bytes in the matrix are substituted one at a time. Thus, there are 16 distinct byte-to-byte transformations. To substitute the bytes using a transformation table, each byte is treated as two hexadecimal digits, where the first digit (left one) specifies the row and the second digit (right one) specifies the column of the substitution table. The value (two hexadecimal digits) at the intersection of the row and the column in the transformation table is the new byte with which the given byte is to be replaced.
Substitute Bytes: It is the first transformation of a round used during encryption. The input to this transformation is a state organized as a 4×4 matrix of bytes. The bytes in the matrix are substituted one at a time. Thus, there are 16 distinct byte-to-byte transformations. To substitute the bytes using a transformation table, each byte is treated as two hexadecimal digits, where the first digit (left one) specifies the row and the second digit (right one) specifies the column of the substitution table. The value (two hexadecimal digits) at the intersection of the row and the column in the transformation table is the new byte with which the given byte is to be replaced.
 Inverse Substitute Bytes: It is used at the decryption side and is the inverse of the Substitute Bytes transformation.
Inverse Substitute Bytes: It is used at the decryption side and is the inverse of the Substitute Bytes transformation.
 Permutation: AES also permutes the bytes. It performs a byte-level permutation (unlike DES, which works on the bit level), such that the order of bits in each byte does not change in the resultant bytes. The two invertible transformations that fall under this category are as follows:
Permutation: AES also permutes the bytes. It performs a byte-level permutation (unlike DES, which works on the bit level), such that the order of bits in each byte does not change in the resultant bytes. The two invertible transformations that fall under this category are as follows:
 Shift Rows: It is used at the encryption side. In this transformation, the bytes in the rows of the input state matrix are shifted to the left, and the number of bytes to be shifted depends on the row number. For example, the row 0 is not shifted at all, the row 1 is shifted 1 byte, row 2 is shifted 2 bytes and row 3 is shifted 3 bytes.
Shift Rows: It is used at the encryption side. In this transformation, the bytes in the rows of the input state matrix are shifted to the left, and the number of bytes to be shifted depends on the row number. For example, the row 0 is not shifted at all, the row 1 is shifted 1 byte, row 2 is shifted 2 bytes and row 3 is shifted 3 bytes.
 Inverse Shift Rows: It is used at the decryption side and is similar to the Shift Rows transformation, except that here the bytes in the rows are shifted to the right.
Inverse Shift Rows: It is used at the decryption side and is similar to the Shift Rows transformation, except that here the bytes in the rows are shifted to the right.
 Mixing: The Substitute Bytes transformation is an intrabyte transformation as it transforms the bytes but does not affect the bits inside the bytes. It also does not take into account the neighbouring bytes. Similarly, the Shift Rows transformation permutes only the bytes but not the bits inside the bytes and, thus, is referred to as a byte-exchange transformation. In contrast, the Mixing is an interbyte transformation in which the bits inside the bytes are changed on the basis of bits in the neighbouring bytes. Mixing transformation takes 4 bytes at a time and combines these bytes to make 4 new bytes. In the combination process, each byte is first -multiplied with a different constant and, then, all the 4 bytes are mixed. For mixing, matrix multiplication is used. AES specifies the following two invertible transformations that fall under this category:
Mixing: The Substitute Bytes transformation is an intrabyte transformation as it transforms the bytes but does not affect the bits inside the bytes. It also does not take into account the neighbouring bytes. Similarly, the Shift Rows transformation permutes only the bytes but not the bits inside the bytes and, thus, is referred to as a byte-exchange transformation. In contrast, the Mixing is an interbyte transformation in which the bits inside the bytes are changed on the basis of bits in the neighbouring bytes. Mixing transformation takes 4 bytes at a time and combines these bytes to make 4 new bytes. In the combination process, each byte is first -multiplied with a different constant and, then, all the 4 bytes are mixed. For mixing, matrix multiplication is used. AES specifies the following two invertible transformations that fall under this category:
 Mix Columns: It is used at the encryption side. This is a column-level transformation that takes one column of input state matrix at a time and transforms it to a new column. For transforming the columns, a constant square matrix is used. The square matrix is multiplied by each column of state matrix resulting into a column. Notice that the bytes multiplication operation is performed in GF(28) field and the bytes addition operation is performed by simply XORing the bits within bytes.
Mix Columns: It is used at the encryption side. This is a column-level transformation that takes one column of input state matrix at a time and transforms it to a new column. For transforming the columns, a constant square matrix is used. The square matrix is multiplied by each column of state matrix resulting into a column. Notice that the bytes multiplication operation is performed in GF(28) field and the bytes addition operation is performed by simply XORing the bits within bytes.
 Inverse Mix Columns: It is used at the decryption side and is similar to Mix Columns transformation except that it uses the inverse of the constant square matrix used in Mix Columns transformation.
Inverse Mix Columns: It is used at the decryption side and is similar to Mix Columns transformation except that it uses the inverse of the constant square matrix used in Mix Columns transformation.
 Key adding: This is the only transformation that makes use of the round key (generated from cipher key) and, thus, is considered an important transformation. To perform key adding transformation, the 128-bit round key is considered as four 32-bit words, and further, each 32-bit word is treated as a column matrix. A self-invertible transformation that falls under this category is as follows:
Key adding: This is the only transformation that makes use of the round key (generated from cipher key) and, thus, is considered an important transformation. To perform key adding transformation, the 128-bit round key is considered as four 32-bit words, and further, each 32-bit word is treated as a column matrix. A self-invertible transformation that falls under this category is as follows:
 Add Round Key: Like Mix Columns transformation, it also operates on one column at a time; however, it uses matrix addition operation rather than matrix multiplication. Each column of the state matrix is XORed with the corresponding key word (column matrix) to produce the new column. This transformation is used in both encryption and decryption.
Add Round Key: Like Mix Columns transformation, it also operates on one column at a time; however, it uses matrix addition operation rather than matrix multiplication. Each column of the state matrix is XORed with the corresponding key word (column matrix) to produce the new column. This transformation is used in both encryption and decryption.
12. What do you mean by key expansion in AES? Explain the key expansion process in AES-128.
Ans.: Key expansion is a process used in AES to generate the round keys from the given cipher key. In AES, the number of round keys generated by this process is always one greater than the number
of rounds. That is, if there are n rounds, the key expansion generates (n+1) keys (say, K0 to Kn), out of which the first round key K0 is used in the Add Round Key transformation before the first round, and the remaining keys (K1 to Kn) are used in the corresponding rounds. In addition, the key expansion generates each round key word-by-word, where each word is an array of 4 bytes. Thus, the total number of words created in n rounds is equal to 4(n+1), denoted as d0, d1,…, d4(n+1)-1.
Key Expansion in AES-128
In AES-128, there are 10 rounds, and the cipher key is 128 bits long. Therefore, the number of keys generated is 11 (K0 to K10), and the number of words created is 44 (d0 to d43). The cipher key of 128 bits is treated as an array of 16 bytes (say, r0 to r15) – that is, four 32-bit words. Before we describe the steps involved in key expansion, we need to know the two routines, RotWord() and SubWord(), as well as round constant RCon, which are used in the process.

RotWord(): The RotWord (which stands for rotate word) routine performs a similar function as that of the Shift Rows transformation, with the exception that it is applied to only one row. It takes a 4-byte word, and shifts each byte of the word to the left with wrapping.

SubWord(): The SubWord (which stands for substitute word) routine performs a similar function as that of the Substitute Bytes transformation, with the exception that it is applied to only 4 bytes (that is, a single word). It takes each byte of a 4-byte word and substitutes it with another byte with the help of transformation table.

RCon: RCon (which stands for round constants) is a 4-byte value where the leftmost byte is non-zero and the rightmost 3 bytes are always zero. As the name implies, this value is fixed for each round. Table 4.2 lists the round constants for 10 rounds of AES-128.
| Round | RCon |
|---|---|
| 1 | (01 00 00 00 00)16 |
| 2 | (02 00 00 00 00)16 |
| 3 | (04 00 00 00 00)16 |
| 4 | (08 00 00 00 00)16 |
| 5 | (10 00 00 00 00)16 |
| 6 | (20 00 00 00 00)16 |
| 7 | (40 00 00 00 00)16 |
| 8 | (80 00 00 00 00)16 |
| 9 | (1B 00 00 00 00)16 |
| 10 | (36 00 00 00 00)16 |
The steps involved in creating 44 words (d0 to d43) from the original cipher key of 16 bytes (r0 to r15) are as follows (see Figure 4.9):
1. The 16 bytes of the cipher key (that is, r0 to r15) form the first four words d0, d1, d2 and d3. That is, d0: = r0r1r2r3, d1: = r4r5r6r7, d2: = r8r9r10r11 and d3: = r12r13r14r15.
2. Create the remaining 40 words using the following process.
for ( i = 4 to 43)do
{
if ( i mod 4)= 0 then
{
s : = SubWord(RotWord( d i-1 ))
ti: = s  RConi/4
di : = ti
RConi/4
di : = ti  di-4
}
else
di: = di-1
di-4
}
else
di: = di-1  di-4
}
di-4
}
Figure 4.9 Key Expansion in AES-128
13. How is the key expansion in AES-192 and AES-256 different from that in AES-128?
Ans.: AES-192 and AES-256 employ a similar key expansion as that of AES-128, however, with a few differences. In AES-192, the cipher key is 192 bits long and is treated as an array of 24 bytes (r0 to r23), that is, six 32-bit words. As there are 12 rounds, the key expansion creates 52 words of round key (d0 to d51), and these words are generated in groups of six. The differences between key expansion in AES-192 and AES-128 are as follows:
1. The 24 bytes of cipher key (that is, r0 to r23) form the first six words (d0 to d5) of the round key.
2. For the remaining words (di, i = 6 to 51), if (i mod 6)= 0 then di: = ti ; else, 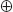 di-6
di-6di: = di-1 . di-6
di-6
On the other hand, in AES-256, the cipher key is 256 bits long and is treated as an array of 32 bytes (r0 to r31), that is, eight 32-bit words. As there are 14 rounds, the key expansion creates 60 words of
round key (d0 to d59) and these words are generated in the groups of eight. The differences between key expansion process in AES-256 and AES-128 are as follows:
1. The 32 bytes of the cipher key (that is, r0 to r31) form the first eight words (d0 to d7) of the round key.
2. For the remaining words (di, i = 8 to 59)

if (i mod 8)= 0 then di: = ti  di-8; else, di: = di-1
di-8; else, di: = di-1  di-8.
di-8.

if (i mod 4)= 0, but (i mod 8) 0, then di: = SubWord(di-1)
0, then di: = SubWord(di-1) 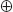 di-8.
di-8.
14. What do you mean by mode of operation in block ciphers? Explain block cipher modes of operation.
Ans.: Modern block ciphers such as DES and AES perform symmetric-key encipherment, thus providing data security. Both DES and AES have been devised to encipher/decipher fixed-size blocks of 64 and 128 bits, respectively. However, in real-life applications, the data to be enciphered is generally of variable size. Thus, some technique is needed to enhance the strength of block ciphers such as DES and AES and to adapt them to such applications so that data of any size can be enciphered. Such technique is referred to as the mode of operation. There are four commonly used block cipher modes of operations that have been suggested by NIST. These modes are discussed in the following sections.
Electronic Code Book (ECB) Mode
This is the simplest mode of operation in which the entire plaintext message is divided into m blocks (P1, P2,…, Pm), with each block containing n (usually n = 64) bits. While breaking the message, if the last block contains less than n bits, padding is used to make it equal to the other blocks.
During encryption, one n-bit block of plaintext (say, Pi) is taken at a time and encrypted using a key K to produce the corresponding n-bit ciphertext block (say, Ci). Each block is encrypted independently of the other blocks, and the same key (say, K) is used for encrypting all the blocks. During decryption also, one block is decrypted at a time, and the same key K is used for decrypting the blocks. Figure 4.10 shows the encryption and decryption processes in the ECB mode.
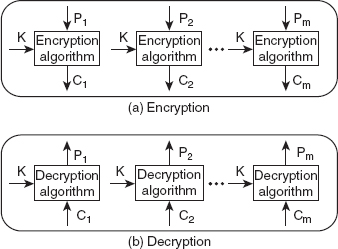
Figure 4.10 Encryption and Decryption in the ECB Mode
In the ECB mode, since all blocks are encrypted independent of each other, a bit error in one block during transmission will not affect any other block; however, it may cause errors in many bits within the same block. In addition, as the same key is used for encrypting all the blocks, if an n-bit block repeats in the plaintext message, the corresponding ciphertext block also repeats in the ciphertext. That is, two same plaintext blocks always result in the same ciphertext blocks. This makes the ECB mode suitable for sending only short messages, such as an encryption key, for example. For long messages, this mode may not be secure, as there are more chances of repetition in long messages.
Cipher Block Chaining (CBC) Mode
This mode of operation overcomes the problem of the ECB mode by ensuring that the same plaintext blocks will not result in the same ciphertext blocks. For this, in the CBC mode, a plaintext block is encrypted based on the previous ciphertext block. In other words, each ciphertext block depends on the corresponding current plaintext block, as well as on all the previous plaintext blocks. Like the ECB mode, the same key (say, K) is used for encrypting all the blocks.
During encryption, each plaintext block (except the first one) is first XORed with the previous ciphertext block, and then encrypted. As there is no ciphertext block prior to the first block, a data block called initialization vector (IV) is used for this. The value of this vector is randomly generated and is agreed upon by the sender and the receiver. During decryption, each ciphertext block is first decrypted using the same key (K) that was used for encryption, and then the decrypted result is XORed with the previous ciphertext block to obtain the corresponding plaintext block. In case of the first ciphertext block, the output of the decryption algorithm is XORed with IV, as used in the encryption process. Figure 4.11 shows the encryption and decryption processes in the CBC mode.
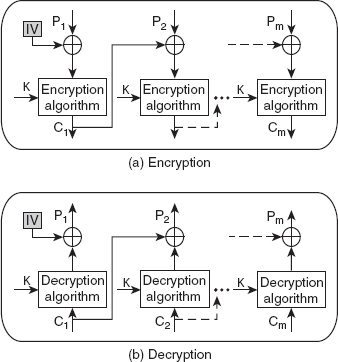
Figure 4.11 Encryption and Decryption in the CBC Mode
Cipher Feedback (CFB) Mode
The block ciphers including DES and AES operate on 64 and 128 blocks of data, respectively, and thus, are not suitable for character-oriented applications where we need to encrypt/decrypt the smaller units (say, 8 bits) at a time. In such situations, stream ciphers prove useful. The CFB is the mode that enables converting DES (or AES) into a stream cipher. As with the CBC mode, the CFB mode also uses an initialization vector (IV) that consists of 64 bits. The contents of IV are stored in the shift register. To understand how the CFB mode works, consider that d bits are to be encrypted/decrypted at a time. The following steps are used during encryption (see Figure 4.12):
1. Encrypt IV, which is stored in the shift register using the block cipher such as DES with key K, to produce an encrypted IV.
2. Take the r leftmost bits of encrypted IV and XOR them with r bits of the plaintext to be encrypted, thus producing an r-bit ciphertext (say, C). Send the ciphertext C to the receiver.
3. Shift the contents of IV stored in the shift register left by r positions, and fill the rightmost r positions with r bits of C.
4. Repeat steps 1 to 3 until the whole plaintext message is encrypted.
Figure 4.12 Encryption in the CFB Mode
During decryption, the same process is used, except that now the XOR operation is performed on the received ciphertext and the output of encryption algorithm to produce the plaintext. It should be noted that the encryption algorithm, and not the decryption algorithm, is used during decryption also.
Output Feedback (OFB) Mode
This mode is similar to the CFB mode, except that in this mode, instead of feeding ciphertext as an input to the shift register in the next stage of the encryption process, the output of IV encryption (that is, encrypted IV) is fed into the shift register. Thus, the ciphertext does not take any part in the encryption process. Figure 4.13 shows the encryption process in the OFB mode.
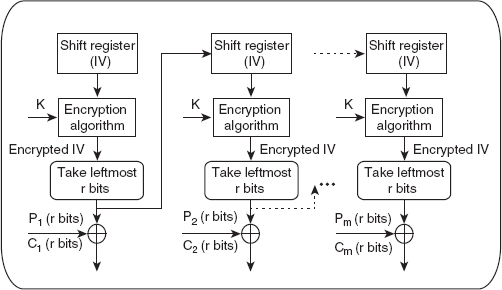
Figure 4.13 Encryption in the OFB Mode
An advantage of the OFB mode is that bit errors are not propagated. This means that if a bit error occurs in the ciphertext during transmission, then only the corresponding plaintext bit will be erroneous, rather than the whole message. However, an attacker can simultaneously make changes to the ciphertext and checksum of the message in a controlled way. Thus, there is no way to detect this change.
Multiple-choice Questions
1. There are _________ encryption rounds in IDEA.
(a) 5
(b) 16
(c) 10
(d) 8
2. DES encrypts/decrypts blocks of _________ bits.
(a) 128
(b) 64
(c) 56
(d) 192
3. The algorithm in the AES cipher was actually given by _________.
(a) Rijndael
(b) IDEA
(c) Blowfish
(d) None of these
4. Which of the following modes of operations does not make use of an initialization vector?
(a) Cipher block chaining
(b) Output feedback
(c) Cipher feedback
(d) Electronic codebook
5. Each round in DES uses _________ S-boxes.
(a) Five
(b) Ten
(c) Eight
(d) Six
6. Which of the following services is based on the IDEA algorithm?
(a) PGP
(b) S/MIME
(c) SET
(d) SSL
7. Which of the following transformations belong to permutation?
(a) Inverse sub-bytes
(b) Shift Rows
(c) Add Round Key
(d) All of these
8. The key expansion in AES-256 creates _________ words.
(a) 44
(b) 52
(c) 60
(d) 54
Answers
1. (d)
2. (b)
3. (a)
4. (d)
5. (c)
6. (a)
7. (b)
8. (c)
1. What are prime numbers and relatively prime numbers?
Ans.: Any positive integer greater than 1 is a prime number if and only if it is divisible by only two integers, 1 and itself. For example, the numbers 2, 3, 5, 7, 11, 13, 17 and 19 are all prime numbers, whereas the numbers 4, 6, 8 and 10 are composite (means not prime), because they have more than two divisors.
Two positive integers a and b are said to be relatively prime, or co-prime, if gcd(a, b)= 1. In other words, two numbers are said to be relatively prime if they have no common factors except the integer 1. For example, the integers 14 and 15 are relatively prime; however, the integers 14 and 16 are not relatively prime because they have a common factor other than the integer 1. Note that the integer 1 is relatively prime with any integer. Also, if n is a prime number, all integers ranging from 1 to n-1 are relatively prime to n.
2. State and prove Fermat's theorem.
Ans.: Fermat's theorem, also called Fermat's little theorem, plays an important role in public-key cryptography. The theorem states that if p is a prime number and x is a positive integer not divisible by p, then:
xp-1 ≡ 1 (mod p)
In other words, we can say that:
xp-1 mod p = 1
Proof
Consider a set of integers Zp={1, 2,…, p-1} where each element of Zp is relatively prime to p.
If all elements of Zp are multiplied by x, and the result is mapped to Zp using modular arithmetic, we get another set (say, S), as shown here:
S = {x mod p, 2x mod p,…, (p-1)x mod p}
As x is not divisible by p, none of the elements of S is zero. Also, no two elements of S are equal. Thus, we can say that the set S contains the elements of Zp, that is, {1, 2,…, p-1} in some order. On multiplying the elements in both the sets and taking the result modulo p, we get:
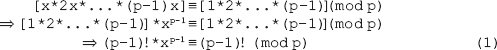
As p and (p-1) are relatively prime, the term (p-1)! can be cancelled out from both sides. Thus, equation (1) becomes:
xp-1 ≡ 1 (mod p)
Hence, proved.
There is another version of Fermat's theorem which states that, if p is a prime number and x is a positive integer, then:
xp ≡ x (mod p)
3. Explain Euler's totient function.
Ans.: Euler's totient function, also called Euler's phi function [denoted as Φ(n)], has an important role in cryptography. The value of this function is the number of positive integers that are smaller than n and relatively prime to n. The set of these numbers is represented by Zn.
A set of rules is to be followed while calculating the value of Φ(n) in the set Zn. These rules are as follows:
Rule 1: Φ(1)= 1
Rule 2: Φ(p)= p-1, if p is a prime number
Rule 3: Φ(m * n)= Φ(m)* Φ(n), if m and n are relatively prime
Rule 4: Φ(pe)= pe-pe-1, if p is prime
To compute Φ(n), suppose that we have two prime numbers p and q, such that p ≠ q and n = pq. Thus, we can write:
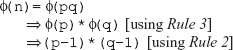
For example, for n = 21
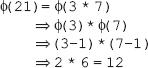
From the preceding example, it is clear that there are 12 integers that are smaller than the number 21 and relatively prime to 21.
4. State and prove Euler's theorem with the help of an example.
Ans.: Euler's theorem is also known as Fermat-Euler theorem or Euler's totient theorem. This theorem has two forms. The first form of Euler's theorem states that for every positive integer x that is relatively prime to n,
xΦ(n) ≡ 1(mod n)
Proof
If n is a prime number, then Φ(n)= n-1. Thus, the preceding equation becomes xn-1 ≡ 1(mod n), which is true by the Fermat's theorem, discussed in Question 2. Now, consider the case when n is not prime.
Let us consider a set R = {a1, a2, …, aΦ(n)}, where each ai is less than n and relatively prime to n. Multiplying each element of the set R by x and taking the result mod n, we get another set S, as shown here:
S = {(xa1 mod n),(xa2 mod n),…,(xaΦ(n) mod n)}
The set S is a permutation of R, because of the following reasons:
 As
As ai and x are relatively prime to n, xai must also be relatively prime to n. Thus, all the elements of S are positive integers that are less than n and relatively prime to n.
 The set
The set S does not contain any duplicate elements. That is, if xai mod n = xaj mod n, then ai = aj.
Therefore, we can write that:
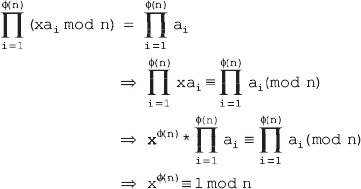
Hence, proved.
The alternative form of Euler's theorem states that:
xΦ(n)+1 ≡ x mod n
Unlike the first form, this form does not require x be relatively prime to n.
5. What is primality testing? What are its categories?
Ans.: In cryptographic algorithms, we often need to create large prime numbers. The selection of such numbers is a very challenging task. Thus, an algorithm is needed that can efficiently check whether a given large number is prime or composite. That is, we need an algorithm that can efficiently perform primality test on numbers. The algorithms for checking the primality are divided into two categories: deterministic and probabilistic.
 Deterministic algorithms: As the name suggests, these algorithms determine whether a given number is prime or not. They accept a number (say,
Deterministic algorithms: As the name suggests, these algorithms determine whether a given number is prime or not. They accept a number (say, p) as input and output the result, either that p is prime or that p is composite. There are two types of deterministic algorithms, which are as follows:
 Basic algorithm: A simple way to check whether a number
Basic algorithm: A simple way to check whether a number p is prime or not is to divide p by all values m (from 2 to p-1) and check whether p is fully divisible by any value of m. If so, then p is composite; else, it is prime.
 Divisibility algorithm: In this algorithm, instead of testing up to
Divisibility algorithm: In this algorithm, instead of testing up to p-1, testing up to only √p is sufficient. The reason behind this is that if p is composite, then it can be factored into two values, and at least one of the values must be less than or equal to √p. Thus, if the number p is divisible by any of the prime numbers less than √p, then it is composite.
 Probabilistic algorithms: As the name suggests, these tests are based on the probability theory and are used to check the probability of a number being prime. These algorithms are also referred to as randomized algorithms. They accept an integer
Probabilistic algorithms: As the name suggests, these tests are based on the probability theory and are used to check the probability of a number being prime. These algorithms are also referred to as randomized algorithms. They accept an integer p and output the probability of p being prime. There are two types of tests based on the probability theory.
 Fermat's primality test: This is a probabilistic test that checks whether a number is prime or not. We check the probability of the Fermat's little theorem to be true or false. As we know that the theorem states that if
Fermat's primality test: This is a probabilistic test that checks whether a number is prime or not. We check the probability of the Fermat's little theorem to be true or false. As we know that the theorem states that if p is prime and x is relatively prime to p such that 1 < x < p ε Zp, then:
xp-1 ≡ 1 (mod p)
To test whether p is prime or not, we pick a random number x from Zp and check whether equality holds. If equality does not hold, then p is composite, whereas if equality holds for many values of x, then p is said to be probably prime or pseudoprime. Usually, it is not possible to check the equality for all values of x. In case we pick such a value of x for which the equality holds, but p is composite, then x is known as a Fermat liar. In contrast, if we do pick a value for x such that the equality fails and p is also composite, then x is known as Fermat witness for the compositeness of p.
 Miller-Rabin test: It is also a probabilistic test to check whether a number taken at random is prime or not. This test returns the result as composite if
Miller-Rabin test: It is also a probabilistic test to check whether a number taken at random is prime or not. This test returns the result as composite if p is not prime, or as inconclusive if p may or may not be a prime number. We check the probability of the number being composite or inconclusive with the help of an algorithm given by Miller and Rabin.
6. Give the Miller-Rabin algorithm for testing primality.
Ans.: The Miller-Rabin algorithm (also known as the Rabin-Miller test) is used to test a large number for primality. It is a polynomial-time algorithm with a run-time complexity of O((log n)3).
As we know, a positive odd integer p can be written in the power of 2 as follows:
p-1 = 2kq
Where, q is an odd number that is obtained by dividing (p-1) by 2, and k is the number of times and k > 0.
For example, let p = 37. Then, p-1 = 36, which can be written as 36 = 22 * 9. Here, 9 is obtained when 36 is divided twice by 2.
In Miller-Rabin algorithm, we take into account two basic properties of prime numbers, which are as follows.
1. If p is a prime number and x is a positive integer (1 < x < p), then x2 mod p = 1 if and only if x mod p = 1 or x mod p = -1. As in modular arithmetic, -1 mod p =(p-1); therefore, x mod p = -1 means x mod p =(p-1). As we know, (x mod p)*(x mod p)= x2 mod p. Hence, whether x mod p = 1 or x mod p = -1, we always get x2 mod p = 1.
2. If p is a prime number greater than 2, we can say that p-1 = 2kq where k > 0 and q is odd, then any one of the following conditions is true:

xq mod p = 1 or xq ≡ 1 (mod p)
 One of the numbers from(
One of the numbers from(xq, x2q, x4q,…, x2(k-1)q, x2kq) is congruent to -1 modulo p. This implies that there is some j in the range(1 ≤ j ≤ k)such that:
x2(j-1)q mod p = -1 or x2(j-1)q mod p = p-1.
After considering these two properties, we can come to the conclusion that a number p can be prime if either the first element of the list (xq, x2q,x4q,…, x2(k-1)q, x2kq) modulo p is equal to 1 or if some element in this list (say, x2(j-1)q) modulo p is equal to p-1. If neither of the conditions is satisfied, the number p is not prime (that is, it is composite).
Here, it is important to note that if the condition is satisfied, it does not necessarily mean that p is prime. That is, even if the condition is satisfied, p may or may not be prime. For example, let p = 2047. Then p-1, that is, 2046, can be written as 2 * 1023, yielding k = 1 and q = 1023. Now, as 21023 mod 2047 = 1, 2047 should be prime; however, it is not. Thus, it is clear that even though a number may satisfy a condition, it may not be prime.
Miller-Rabin algorithm
Let p be an integer to be checked for primality. The algorithm returns the result as composite if p is not prime and inconclusive if p may or may not be a prime number.
1. Find integers k and q where k > 0 and q is odd such that (p-1 = 2kq).
2. Choose a random integer x such that 1< x < p-1
3. S:= xq mod p
4. If S = 1, then print (‘inconclusive’)and exit
5. for j = 0 to k-1
{
S:= x2jq mod p //equivalent to S:= S2 mod p
if S = p-1
print(‘inconclusive’)and exit
}
6. print(‘composite’)
7. Describe and illustrate the Chinese Remainder Theorem.
Ans.: Chinese Remainder Theorem (CRT) is so named as it was discovered by the Chinese mathematician Sun-Tsu in around 100 AD. It is used to solve a set of congruent equations with a single variable but different moduli, which are relatively prime. Consider such a set of equations as shown here:
a = x1 mod m1
a = x2 mod m2
.
.
.
a = xk mod mk
All these equations have a unique solution if the moduli for the equations are pair-wise relatively prime, that is, gcd(mi, mj) = 1. In case the moduli are not relatively prime but satisfy other conditions, then even we can have the solution. In cryptography, we prefer to solve the equations with relatively prime moduli.
The solution to the set of simultaneous equations can be obtained by performing the following steps:
1. Find the common modulus, M = m1* m2*…* mk.
2. Find M1 = M/m1, M2 = M/m2,…, Mk = M/mk.
3. Find the multiplicative inverse of M1, M2,…, Mk using the corresponding moduli m1, m2,…, mk. Let the inverses be M1-1, M2-1,…, Mk-1.
4. The solution to the simultaneous equations is:
a =(x1 * M1 * M1-1 + x2 * M2 * M2-1 +…+ xk * Mk * Mk-1) mod M
8. Define the following terms:
(a) Finite multiplicative group
(b) Order of the group
(c) Order of an element
(d) Primitive roots of a group
(e) Cyclic group
Ans.: (a) Finite multiplicative group: A finite multiplicative group is often used in cryptography. It is represented as G = < , *>
, *>
Where:
G = finite multiplicative group
1 and n-1 that are relatively prime to n
* = the multiplication operation
The identity element (e) of the finite multiplicative group G is equal to 1.
(b) Order of the group: As we know, the order of a group is the number of elements in the group. For a finite multiplicative group G = <, the order of the group is  , *>
, *>Φ(n), where Φ(n) is the Euler's totient function.
(c) Order of an element: For a finite multiplicative group G = <, the order of an element (say, 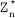 , *>
, *>a), represented as Ord(a), is the smallest integer i such that ai ≡ e(mod n), where e is the identity element of the group G. Here, the value of e is 1.
(d) Primitive roots of a group: For a finite multiplicative group G = <, the primitive roots are the elements that have the order equal to 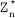 ,*>
,*>Φ(n). The number of primitive roots in a group is equal to Φ(Φ(n)).
(e) Cyclic group: If a finite multiplicative group G = < has primitive roots, it is called a cyclic group. Each primitive root of the cyclic group can be used to generate the elements of the set 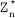 , *>
, *>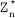
x is a generator, then elements can be created using xa modulo n, where a is an integer ranging from 1 to Φ(n), as shown here:
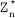 ={x1 mod n, x2 mod n, x3 mod n,…, xΦ(n) mod n}
={x1 mod n, x2 mod n, x3 mod n,…, xΦ(n) mod n}
Notice that a finite multiplicative group G = < is always cyclic if 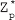 , *>
, *>p is a prime number.
9. Write a short note on discrete logarithmic problems.
Ans.: In cryptography, exponentiation and modular logarithm are often used. Exponentiation and logarithm are reverse of each other. Whenever exponentiation is used to encrypt the plaintext or decrypt the ciphertext, the opponent can use logarithm to attack. Thus, it is required to identify how difficult it is to reverse the exponentiation. An approach to determine this is to use the concept of discrete logarithm.
Consider a finite multiplicative group G = <, where 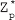 , *>
, *>p is prime. The elements of this group are the integers from 1 to p-1. In addition, the group is cyclic, as p is prime and thus has primitive roots. The primitive roots of such a group can be considered as the base of the logarithm. Thus, in case the group has m primitive roots, the calculation can be performed in m different bases.
Let us consider a as a primitive root of group G. Then, an element (say, y) of 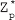
y = ax mod p
Where, x is an integer ranging from 1 to Φ(p) (which is p-1, in this case). Suppose we are given the value of y, and we are to find the value of x. Such type of problem is referred to as a discrete logarithmic problem, and the solution to this problem is given as:
x = logay mod p
That is, we need to find the log of y in base a, and then take the result mod p.
10. Find out the result of 312 mod 11.
Ans.: We can write:
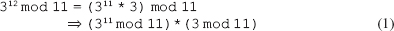
Now, according to second version of Fermat's theorem, xp ≡ x(mod p)or xp mod p = x. Thus, we get (311 mod 11)= 3. Also, (3 mod 11)= 3. Putting both these values in equation (1), we have:
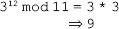
11. Find out the result of 512 mod 13.
Ans.: We can write:
512 mod 13 = 513-1 mod 13
Now, according to Fermat's theorem for a prime number p, which states that xp-1 mod p = 1, we have:
513-1 mod 13 = 1, as 13 is a prime number.
12. Find Φ(7).
Ans.: As 7 is a prime number, according to Rule 2 of the Euler's totient function [f(n)= n-1], we have:
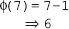
This implies that there are six positive integers that are less than 7 and relatively prime to 7. These integers include 1, 2, 3, 4, 5 and 6.
13. Find Φ(10).
Ans.: The integer 10 is a multiple of 5 and 2, therefore, we can write:
Φ(10)= Φ(5*2)
As 5 and 2 are relatively prime, by applying Rule 3 of Euler's totient function [Φ(m * n)= Φ(m)* Φ(n)], we can write:
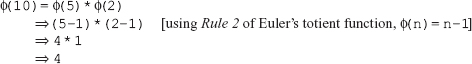
14. Check whether 89 is a prime.
Ans.: To check 89 for primeness, we can apply the divisibility test, where we check whether 89 is divisible by any of the prime numbers less than √89. Now, the integral value of √89 is 9 and the prime numbers less than 9 are {2, 3, 5, 7}. As 89 is not divisible by any of these numbers, it is a prime.
15. Apply Miller-Rabin's algorithm and use base 2 to test whether the number 561 passes the test.
Ans.: Using Miller-Rabin algorithm, explained in Question 6, we can test the number 561 as follows:

As for no value of j, S is equal to 560. Thus, 561 is composite.
16. Solve the following simultaneous congruence using Chinese Remainder Theorem to find the value of a.
a ≡ 2 mod 3
a ≡ 3 mod 5
a ≡ 2 mod 7
Ans.: Applying Chinese Remainder Theorem, explained in Question 7, the solution to the given equations is obtained as follows:
Step 1: Given m1 = 3, m2 = 5, m3 = 7
Thus, the common modulus, M = 3*5*7 = 105
Step 2: Compute M1, M2 and M3.
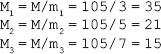
Step 3: Compute the multiplicative inverse of M1, M2 and M3 in modulo m1, m2 and m3, respectively.
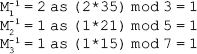
Step 4: The solution to the simultaneous equations is as follows:
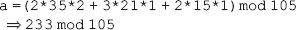
Thus, the value of a is 23.
17. Find the order of all the elements in G = <. Also find the primitive roots in the group 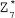 ,*>
,*>G.
Ans.: For the group G = <, the set  , *>
, *> contains those integers between 1 and 6 that are relatively prime to 7. That is,
contains those integers between 1 and 6 that are relatively prime to 7. That is,  = {1, 2, 3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6}= Φ(7)= 6.
For each element a of the set 
i (from 1 to 6), the condition ai ≡ 1(mod n), that is, ai mod n = 1, holds true. That value of i will be the order of the element.
1. For a = 1,
11 mod 7 = 1
Thus, the order of element 1, that is, Ord(1)= 1.
2. For a = 2,
21 mod 7 = 2 ≠ 1
22 mod 7 = 4 mod 7 = 4 ≠ 1
23 mod 7 = 8 mod 7 = 1
Thus, the order of element 2, that is, Ord(2)= 3.
3. For a = 3,
31 mod 7 = 3 ≠ 1
32 mod 7 = 9 mod 7 = 2 ≠ 1
33 mod 7 = 27 mod 7 = 6 ≠ 1
34 mod 7 = 81 mod 7 = 4 ≠ 1
35 mod 7 = 243 mod 7 = 5 ≠ 1
36 mod 7 = 729 mod 7 = 1
Thus, the order of element 3, that is, Ord(3)= 6.
4. For a = 4,
41 mod 7 = 4 mod 7 = 4 ≠ 1
42 mod 7 = 16 mod 7 = 2 ≠ 1
43 mod 7 = 64 mod 7 = 1
Thus, the order of element 4, that is, Ord(4)= 3.
5. For a = 5
51 mod 7 = 5 ≠ 1
52 mod 7 = 25 mod 7 = 4 ≠ 1
53 mod 7 = 125 mod 7 = 6 ≠ 1
54 mod 7 = 625 mod 7 = 2 ≠ 1
55 mod 7 = 3125 mod 7 = 3 ≠ 1
56 mod 7 = 15625 mod 7 = 1
Thus, the order of element 5, that is, Ord(5)= 6.
6. For a = 6,
61 mod 7 = 6 ≠ 1
62 mod 7 = 36 mod 7 = 1
Thus, the order of element 6, that is, Ord(6)= 2.
Only the elements 3 and 5 have the order equal to Φ(7), that is, 6, and therefore the primitive roots of the group G are 3 and 5.
18. Find the value of x in the group G =(for the following cases with the help of the given table. ,*)
,*)
(a) 4 ≡ 3x mod 7
(b) 6 ≡ 5x mod 7
Ans.: For the group G =( and  ,*), Φ(7)= 6
,*), Φ(7)= 6 ={1, 2, 3, 4, 5, 6}
={1, 2, 3, 4, 5, 6}a = bx mod n. These equations can be solved using the table for each 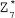
(a) 4 ≡ 3x mod 7
Here, a = 4. Thus, x = log34 mod 7
From the given table, it is clear that log34 = 4. Therefore,
x = 4 mod 7
 4
4
(b) 6 ≡ 5x mod 7
Here, a = 5. Thus, x = log56 mod 7
From the given table, it is clear that log56 = 3. Therefore,
x = 3 mod 7
 3
3
Multiple-choice Questions
1. What is the value of Φ(1)?
(a) Zero
(b) One
(c) Not defined
(d) None of these
2. The gcd of 14 and 15 is __________.
(a) One
(b) Two
(c) Three
(d) Four
3. Two positive integers a and b are said to be relatively prime if __________.
(a) Their gcd is 1
(b) They have no common prime factors
(c) If 1 is their only common divisor
(d) All of these
4. Which of the following is used for testing primality?
(a) Fermat's primality test
(b) Miller-Rabin
(c) Divisibility test
(d) All of these
5. Chinese remainder theorem is given by __________
(a) Fermat
(b) Euler
(c) Sun-Tsu
(d) Miller and Rabin
6. The number of primitive roots in a group is computed by __________
(a) Φ(Φ(n))
(b) Φ(n)
(c) Ord(n)
(d) None of these
Answers
1. (b)
2. (a)
3. (d)
4. (d)
5. (c)
6. (a)
1. What are the requirements of asymmetric-key cryptography?
Or
What are the characteristics that an asymmetric-key cryptographic algorithm must possess?
Ans.: Asymmetric-key cryptography requires the use of two different keys: the public key for encryption and private key for decryption. The public key is known to everyone, whereas the private key is known to its owner only. Diffie and Hellman laid out some requirements that must be fulfilled by the algorithms used for asymmetric-key cryptography. These requirements are listed below:
 It should be easy for the receiver to generate the pair of keys (public and private).
It should be easy for the receiver to generate the pair of keys (public and private).
 It should be easy for the sender to generate the ciphertext from the original message (that is, the plaintext) with the help of the receiver's public key.
It should be easy for the sender to generate the ciphertext from the original message (that is, the plaintext) with the help of the receiver's public key.
 It should be easy for the receiver to decrypt the ciphertext generated by the sender by using its private key in order to recover the original message.
It should be easy for the receiver to decrypt the ciphertext generated by the sender by using its private key in order to recover the original message.
 It should be infeasible for an intruder to determine the private key of the receiver, even if he or she knows the public key of the receiver.
It should be infeasible for an intruder to determine the private key of the receiver, even if he or she knows the public key of the receiver.
 It should be infeasible for an intruder to determine the original message even if he or she knows the public key of the receiver as well as the ciphertext.
It should be infeasible for an intruder to determine the original message even if he or she knows the public key of the receiver as well as the ciphertext.
 It should be possible to use any of the two keys (public or private) for encryption and decryption. That is, it should be possible to encrypt the message with any one of the keys and decrypt it using the other.
It should be possible to use any of the two keys (public or private) for encryption and decryption. That is, it should be possible to encrypt the message with any one of the keys and decrypt it using the other.
2. Explain the RSA cryptosystem.
Ans.: In 1978, a group at MIT discovered a strong method for public-key encryption. It is known as RSA, the name derived from the initials of its three discoverers Ron Rivest, Adi Shamir, and Len Adleman. RSA cryptosystem is the most widely accepted asymmetric-key algorithm; in fact, most of the practically implemented security systems are based on RSA. The algorithm requires keys of at least 1024 bits for good security. This algorithm is based on some principles from number theory, which states that determining the prime factors of a large number is extremely difficult.
RSA Key Generation
Let A and B be two users who wish to communicate. Suppose that A wants to send a message securely to B. To encrypt the message, A needs to know B's public key. Thus, B uses the following steps to generate his or her public and private keys.
1. Choose two large distinct prime numbers, p and q (about 1024 bits), such that p ≠ q.
2. n: = p*q
3. Φ(n): =(p-1)*(q-1)
4. Choose a number E such that 1 < E < Φ(n), and such that E is relatively prime to Φ(n). The public (encryption) key is (E, n), which is announced publicly.
5. Find another number D such that E * D = 1 mod Φ(n), that is, D = E-1 mod Φ(n). In other words, D is the inverse of E modulo Φ(n). The private (decryption) key is D, which is kept secret.
An important property of RSA algorithm is that the roles of E and D can be interchanged. As the number theory suggests, it is very hard to find the prime factors of a large number n, and hence it is extremely difficult for an intruder to determine the private key D using just E and n.
RSA Encryption and Decryption
In RSA, modular exponentiation is used for performing encryption and decryption. For example, if A has to send a message to B using B's public key (E, n), A encrypts the plaintext (P) to produce the ciphertext (C), as shown here:
C = PE mod n
After B has received the ciphertext (C), he or she decrypts the ciphertext using its private key (D) to get back the original plaintext (P) as shown here.
P = CD mod n
3. Discuss the different attacks on RSA.
Ans.: Although RSA is a secure algorithm used for encryption in public-key cryptography, there are still some weaknesses that enable an attacker to crack the security of the algorithm. There are several attacks that have been predicted on the basis of weak plaintext, parameter selection or inappropriate implementation. These attacks are discussed as follows:
 Factorization attack: This attack is possible if the value of
Factorization attack: This attack is possible if the value of n is small, so that the intruders can easily factorize n and obtain the value of p and q (as n = p × q). As the value of e is public, it may further result in obtaining the value of Φ(n) and d (as d = e-1 mod (p-1)(q-1)). Thus, by using all these values, an intruder can now decrypt any encrypted plaintext and crack the security. To prevent such an attack, n must be more than 300 decimal digits, so that it becomes infeasible to factorize such a long value of n.
 Chosen-ciphertext attack: This attack tries to get the plaintext from the ciphertext by using the multiplicative property of RSA. Suppose the sender sends the ciphertext (
Chosen-ciphertext attack: This attack tries to get the plaintext from the ciphertext by using the multiplicative property of RSA. Suppose the sender sends the ciphertext (C) to the receiver and an intruder intercepts it. Now, the intruder sends fake ciphertext, say Y, to the receiver by choosing a random integer X. As the receiver is unaware about the interception of the original ciphertext, he or she decrypts the fake ciphertext by performing Yd mod n to get Z. Thus, an intruder can now easily get the plaintext (P), as P = Z * X-1 mod n. That is, an intruder needs to find only the multiplicative inverse of X to get the original plaintext. Therefore, the name of attack is chosen-ciphertext attack, as only the particular ciphertext was chosen to know the corresponding plaintext.
 Timing attack: This is a cipher-text-only attack that was unveiled by Paul Kocher. In this attack, an intruder determine a private key by keeping track of how long a computer takes to decrypt the encrypted plaintext. That is, variable timing in evaluation helps an intruder find the value of each bit in
Timing attack: This is a cipher-text-only attack that was unveiled by Paul Kocher. In this attack, an intruder determine a private key by keeping track of how long a computer takes to decrypt the encrypted plaintext. That is, variable timing in evaluation helps an intruder find the value of each bit in d. This means that an intruder can now perform bit-by-bit analysis of the exponential. Such an attack can be prevented if random delays are added to exponentiation, such that the underlying hardware takes a random amount of time to process each. In addition, the concept of blinding can also be used. In this concept, the ciphertext is multiplied by a random number before evaluation. Thus, an intruder will be unable to decipher the ciphertext bits and, therefore, bit-by-bit analysis can be prevented.
 Plaintext attack: In this attack, an intruder already knows something about the plaintext. This helps the intruder to also know about the fact that the ciphertext is the permutation of the plaintext. Thus, an intruder can now compute all the possible messages until the result is equal to the ciphertext intercepted.
Plaintext attack: In this attack, an intruder already knows something about the plaintext. This helps the intruder to also know about the fact that the ciphertext is the permutation of the plaintext. Thus, an intruder can now compute all the possible messages until the result is equal to the ciphertext intercepted.
 Common modulus attack: In this attack, a common modulus is used by a group of people. That is, a whole group agrees for a trusted third party to select the values of two prime numbers
Common modulus attack: In this attack, a common modulus is used by a group of people. That is, a whole group agrees for a trusted third party to select the values of two prime numbers p and q, computes n and Φ(n) and then creates exponents (ei ,di) for each person belonging to the group. By doing this, any person who is a member of the group can decrypt the ciphertext by factoring n and can also compute the receiver's private exponent (dr) . Therefore, to prevent such attack, the modulus must not be shared, and each person in the group must calculate his or her own modulus.
4. Discuss the uses of public-key cryptography in relation to key distribution.
Ans.: One of the major problems in secret-key cryptography is that of key distribution, which can be overcome by the use of public-key cryptography. The two aspects that must be taken into account for using public-key cryptography include the distribution of public keys and the use of public-key encryption for the distribution of secret keys.
Distribution of Public Keys
There are several schemes that have been used for the distribution of public keys. These schemes are as follows:
 Public announcement: The main focus of public-key encryption is on the fact that the public key should be public; that is, a user can send his or her public key to any other user or broadcast it to a large community. Though this approach is convenient, it has some drawbacks. The main problem is that of forgery. That is, anyone can forge the key while it is being transmitted. For example, someone could pretend to be user
Public announcement: The main focus of public-key encryption is on the fact that the public key should be public; that is, a user can send his or her public key to any other user or broadcast it to a large community. Though this approach is convenient, it has some drawbacks. The main problem is that of forgery. That is, anyone can forge the key while it is being transmitted. For example, someone could pretend to be user A and send a public key to another user or broadcast it to many users. Until the original user A comes to know about this forgery and alerts other users, the forger is able to read all the messages intended for user A.
 Public directory: As the public announcement scheme for the distribution of public keys was not too secure and there were chances of forgery, a new scheme was introduced, in which a dynamic directory having the name and public key entry for each user is maintained and distributed by some trusted authority. This approach assumes that the public key of the authority is known to everyone, however the corresponding private key is known only to the authority. Each user has to register his or her public key with the directory authority. The authority either publishes the entire directory periodically in a widely circulated newspaper, or the user can access the directory electronically. The user can replace its existing key with a new one as per his or her choice. Although this scheme is more secure than public announcement, it has some weaknesses. If anyone is able to compute the private key of the directory authority, the person would get the authority to pass around the fake public keys and, later, may pretend to be a genuine user and eavesdrop on the messages being sent to any other user. The fake user may also read or alter the records kept by the authority.
Public directory: As the public announcement scheme for the distribution of public keys was not too secure and there were chances of forgery, a new scheme was introduced, in which a dynamic directory having the name and public key entry for each user is maintained and distributed by some trusted authority. This approach assumes that the public key of the authority is known to everyone, however the corresponding private key is known only to the authority. Each user has to register his or her public key with the directory authority. The authority either publishes the entire directory periodically in a widely circulated newspaper, or the user can access the directory electronically. The user can replace its existing key with a new one as per his or her choice. Although this scheme is more secure than public announcement, it has some weaknesses. If anyone is able to compute the private key of the directory authority, the person would get the authority to pass around the fake public keys and, later, may pretend to be a genuine user and eavesdrop on the messages being sent to any other user. The fake user may also read or alter the records kept by the authority.
 Public-key authority: In public directory scheme, if the private key of the authority is stolen, then it may result in loss of data. Thus, to achieve stronger security for public-key distribution, a tighter control needs to be provided over the distribution of public keys from the directory. In this case also, a central authority maintains the dynamic directory of the public keys of all the users. The user knows only the public key of the authority, while the corresponding private key is secret to the authority.
Public-key authority: In public directory scheme, if the private key of the authority is stolen, then it may result in loss of data. Thus, to achieve stronger security for public-key distribution, a tighter control needs to be provided over the distribution of public keys from the directory. In this case also, a central authority maintains the dynamic directory of the public keys of all the users. The user knows only the public key of the authority, while the corresponding private key is secret to the authority.
To understand how the public-key authority scheme works, consider two users A and B who wish to communicate securely. To enable communication, the following steps are used.
1. A sends a timestamped message containing a request for the current public key of B to the public-key authority.
2. The authority responds by sending A a message that is encrypted using the private key of authority (say, Pauthority ). The user A attempts to decrypt the message using the authority's public key. If the message gets decrypted, A is assured that the message has been sent by the authority itself. The message sent by the authority contains the following:

B's public key (say, PUBB), which can be used by A to send messages to B.
 The original request sent by
The original request sent by A, so that A can match the message received from the authority with its corresponding request, and also verify that the request was not altered before reaching the authority.
 The original timestamp, so that
The original timestamp, so that A can verify whether the message is a new one containing the current public key of B, or an old message containing any other public key.
3. A stores B's public key and uses it to encrypt the message destined for B containing an identifier of A (say, IA) and a nonce N1, which uniquely identifies this transaction.
4. B also follows the same method to retrieve A's public key from the authority. It stores the A's public key for future use. Now, both A and B have got the public keys of each other and, thus, may start exchange messages.
5. B sends a message to A, encrypting it with the public key of A (PUBA). The message contains A's nonce N1 as well as B's nonce N2. As the message could have been decrypted by B only, the inclusion of N1 in the message assures A that the corresponding user is B.
6. A returns N2, encrypted with B's public key (PUBB), to assure B that the corresponding user is A.
Note that the first four steps need not to be followed each time, as the users A and B can store the public keys of each other for future use. This technique is known as caching. However, the users should periodically request for fresh or new copies of the public keys.
 Public-key (or digital) certificates: A better approach where a user can exchange keys without communicating to the public-key authority is to use digital certificates—an electronic document that signifies the association between the user and his/her public key. A certificate authority, such as a government agency or some trusted institution, issues a certificate to each user, which contains a public key and the identifier of the key owner. The certificate is signed by the certificate authority. A user can present his or her public key to the authority to get the certificate. The user can then publish his or her certificate. Now, any other user wishing to get the public key can obtain the certificate and verify its validity by means of the attached trusted signature. The user can also send his or her key information to another user by transmitting the certificate. Users can easily verify that the certificate has been generated by the authority and that it is not a fake certificate. Moreover, only the certificate authority can create or update the certificates.
Public-key (or digital) certificates: A better approach where a user can exchange keys without communicating to the public-key authority is to use digital certificates—an electronic document that signifies the association between the user and his/her public key. A certificate authority, such as a government agency or some trusted institution, issues a certificate to each user, which contains a public key and the identifier of the key owner. The certificate is signed by the certificate authority. A user can present his or her public key to the authority to get the certificate. The user can then publish his or her certificate. Now, any other user wishing to get the public key can obtain the certificate and verify its validity by means of the attached trusted signature. The user can also send his or her key information to another user by transmitting the certificate. Users can easily verify that the certificate has been generated by the authority and that it is not a fake certificate. Moreover, only the certificate authority can create or update the certificates.
Distribution of Secret Keys using Public-key Cryptography
The public-key encryption can be exclusively used for providing distribution of secret keys that are to be used for conventional encryption. There are certain schemes for this, which are described as follows:
 Simple method: In this method, a session is created between the two users who wish to communicate (say,
Simple method: In this method, a session is created between the two users who wish to communicate (say, A and B). When A wants to communicate with B, he or she first creates a pair of public and private keys. Then, A transmits to B a message that contains the public key and A's identifier. B creates a secret key, encrypts it with the public key of A, and sends it to A. A recovers the secret key by decrypting the received encrypted message using his or her private key. At this point, both A and B know the secret key. After exchanging the secret key, A discards both the public and private keys, and B discards the public key. Now, both A and B can securely communicate using conventional encryption and the secret key.
The main advantage of this technique is that no keys exist before the start of the communication and none exists after the communication ends. Therefore, the risk of compromising the keys is minimal, and the communication is secure from eavesdropping. Note that the technique is well suited when the only threat is eavesdropping, as it does not provide confidentiality and assure authenticity of the message.
 Distribution with confidentiality and authentication: This method provides protection against both active and passive attacks. To prevent the transmission of the message from attacks, assuming that
Distribution with confidentiality and authentication: This method provides protection against both active and passive attacks. To prevent the transmission of the message from attacks, assuming that A and B have already exchanged their public keys by any of the earlier-discussed schemes, the following steps take place:
1. A sends a message to B, encrypted with the public key of B, say PUBB. The message contains an identifier of A (say, IA) and a nonce N1, which is used to identify this transaction uniquely.
2. B sends a message to A encrypted with the public key of A (say, PUBA). The message contains A's nonce N1 as well as B's nonce N2. Since only B could have decrypted the message sent by A, the inclusion of B's nonce in the message assures A that the corresponding user is B. Similarly, A sends B's nonce N2, encrypted with B's public key, to assure B that the corresponding user is A.
3. A chooses a secret key (say, SCRA), encrypts it with its private key (PRVA) and sends a message m, encrypted with B's public key (PUBB), as shown here:
m = EPUBB[EPRVA[SCRA]]
Encrypting the message m with B's public key ascertains that only B can read it, and encrypting the message with A's private key ascertains that only A could have sent it.
4. Now, B decrypts the message by computing DPUBA[DPRVB[m]], thus recovering the secret key. This method ensures both confidentiality and authenticity in the exchange of a secret key.
 Hybrid method: This method uses the key distribution centre (KDC), in which a secret master key is shared with each user. The role of KDC is to distribute the session secret keys, encrypted using the master key. A public-key scheme is used for the distribution of the session key. Generally, the applications in which session keys often change, the use of public-key encryption for distributing the secret session keys could degrade the overall system's performance. This is because relatively high computational efforts are required for the public-key's encryption and decryption.
Hybrid method: This method uses the key distribution centre (KDC), in which a secret master key is shared with each user. The role of KDC is to distribute the session secret keys, encrypted using the master key. A public-key scheme is used for the distribution of the session key. Generally, the applications in which session keys often change, the use of public-key encryption for distributing the secret session keys could degrade the overall system's performance. This is because relatively high computational efforts are required for the public-key's encryption and decryption.
The main advantage of this three-level hierarchy is that public-key encryption is rarely used to update the master key between a user and a KDC. Moreover, the scheme is compatible with existing KDC schemes and, thus, can be overlaid on existing schemes with minimal changes required.
5. Discuss Diffie-Hellman key exchange algorithm. Also discuss about its security.
Ans.: Diffie-Hellman key exchange is the first published public-key algorithm that was published in 1976 by Whitefield Diffie and Martin Hellman. This algorithm was devised for the exchange of secret keys between the communicating users in a secure manner. It allows two users to securely exchange a key that can be further used for encryption of messages. Notice that this algorithm can be used only for the exchange of keys, and not for encryption and decryption.
Diffie-Hellman key exchange algorithm enables two users to establish a symmetric session (secret) key without requiring the use of KDC. This is what is referred to as the symmetric-key agreement. Once both the communicating parties have agreed (exchanged) on the common secret key, then a symmetric-key encryption algorithm can be used for encryption and decryption of messages.
Diffie-Hellman algorithm
Consider two users A and B who want to communicate with each other securely over an insecure network. Initially, both A and B need to agree upon a key that is to be used for encryption and decryption of the messages. For this, they can follow the Diffie-Hellman key exchange algorithm, which is given below:
1. Select two numbers p and q by the mutual agreement of A and B, such that p is prime, q is a primitive root of p and q < p. There is no need to keep these two numbers secret.
2. A selects a random number XA (less than p), which becomes his or her private key. Then it computes its public key, YA, as shown here:
YA = qXA mod p
A sends its public key YA to B.
3. B selects a random number XB (less than p), which becomes his or her private key. Then, it computes its public key, YB, as shown here:
YB = qXB mod p
B sends its public key YB to A.
4. After exchanging the public keys, both A and B compute the common secret key(K). A generates the secret key as shown here:
K =(YB)XA mod p
B generates the secret key as shown here:
K =(YA)XB mod p
Proof of algorithm
To show that both A and B have computed the same secret key, we need to prove that the calculation of K by A and B produce the identical results.

Hence, proved.
Security of the Diffie-Hellman algorithm
In Diffie-Hellman algorithm, the private keys XA and XB are secret, while the numbers p and q and the public keys YA and YB are known to everyone. Thus, an opponent has p,q,YA and YB to work with. To determine the key using the available information, the opponent has to use the discrete logarithm. For example, if the opponent wants to find the private key of user A, then he or she has to perform the following calculation:
XA = dlogq,p(YA)
After computing XA, the opponent can compute the common secret key (K) in the same way that A computed it. Since it is difficult to compute the discrete logarithm in comparison to computing exponentials modulo a prime number, the security of the Diffie-Hellman algorithm depends on this fact. In case of large prime numbers, it is infeasible to compute the discrete logarithm and, thus, to break the security of the Diffie-Hellman algorithm.
5. List some advantages of the Diffie-Hellman algorithm.
Ans.: Some advantages of the Diffie-Hellman key exchange algorithm are as follows:
 Secret keys are generated as and when required. Thus, they need not be stored for a long time, thereby making them less vulnerable to attacks.
Secret keys are generated as and when required. Thus, they need not be stored for a long time, thereby making them less vulnerable to attacks.
 No pre-existing infrastructure is required for key exchange. The communicating parties just have to agree upon the values of global variables
No pre-existing infrastructure is required for key exchange. The communicating parties just have to agree upon the values of global variables p and q.
6. What are the limitations of the Diffie-Hellman algorithm?
Ans.: Although the Diffie-Hellman key exchange algorithm allows two communicating parties to securely exchange the key over an insecure network, there are a number of weaknesses to this algorithm, which are given below:
 It does not provide any information regarding the identities of the users exchanging the key. In other words, it does not authenticate the communicating users.
It does not provide any information regarding the identities of the users exchanging the key. In other words, it does not authenticate the communicating users.
 It is vulnerable to man-in-the-middle-attack, where a third user (say,
It is vulnerable to man-in-the-middle-attack, where a third user (say, C) pretends to be user B while communicating with A and pretends to be user A while communicating with B, thereby intercepting their messages. This attack is discussed in the next question.
 It involves a lot of computations and, thus, is subject to clogging attacks . In this attack, an opponent requests for a large number of keys, thus keeping the victim busy in doing unnecessary calculations rather than doing the real work.
It involves a lot of computations and, thus, is subject to clogging attacks . In this attack, an opponent requests for a large number of keys, thus keeping the victim busy in doing unnecessary calculations rather than doing the real work.
7. Explain the man-in-the-middle attack.
Ans.: As the Diffie-Hellman algorithm does not authenticate the users exchanging the keys, it is vulnerable to man-in-the-middle attacks, also referred to as the bucket brigade attack. To understand this attack, consider that A and B are two users who want to communicate and, thus, exchange their keys using the Diffie-Hellman algorithm. Let C be an opponent who wants to intercept the communication between A and B. Now, the man-in-the-middle attack proceeds as follows:
1. A sends a message containing its public key (YA) to B.
2. C intercepts this message, stores A's public key and sends a new message containing its public key (YC) and A's user ID to B.
3. On receiving the message, B saves the C's public key (YC) with A's user ID.
4. B sends a message containing its public key (YB) to A.
5. The opponent C intercepts this message, stores B's public key (YB) and sends a new message containing its public key (YC) and B's user ID to A.
6. On receiving the message, A saves C's public key (YC) with B's user ID.
7. A computes the secret key K1 based on its private key XA and C's public key YC as shown here:
K1 =(YC)XA mod p
8. B computes the secret key K2 based on its private key XB and C's public key YC, as shown here:
K2 =(YC)XB mod p
9. C computes K1 using its private key XC and YA and computes K2 using XC and YB as shown here:
K1 =(YA)XC mod p
K2 =(YB)XC mod p
At this point, A and B think that they have shared a common secret key; however, actually A and C have shared the key K1, whereas B and C have shared the key K2. The opponent C is now able to trap all the messages coming from A to B and B to A, without letting A and B know that their communication is shared with C. This happens in the following way:
1. A sends a message m encrypted with key K1 to B.
2. C intercepts the encrypted message and decrypts it to obtain the original message.
3. C sends either the same message (m) or a modified message (m') to B, encrypted using the key K2.
B receives the message assuming that it has come from A. A similar thing happens when B sends a message to A. This way, C comes in the middle of the communication between A and B and, therefore, the attack is named so.
8. What is the ElGamal encryption system? Explain its encryption and decryption processes.
Ans.: The ElGamal encryption system is a public-key cryptosystem based on the concept of Diffie-Hellman key agreement. It was discovered by Taher ElGamal in 1984. It is based on the discrete logarithm problem. To understand this problem, consider that p is a large prime number, q is an integer and e1 is a primitive root in the group G = <. Now, it is easy to compute 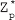 , *>
, *>e2 = e by using fast exponential algorithms. However, if  mod p
mod pe1, e2 and p are given, then it is difficult to calculate q = log(e1 * e2)mod p. This is what is known as the discrete logarithm problem. Thus, the security of ElGamal depends on the complexity of computing discrete logarithms.
The Elgamel encryption system consists of three different components, and separate algorithms are defined for them. The components are key generator, encryption algorithm and decryption algorithm.
ElGamal key generation
Suppose A and B are the communicating parties, and A wishes to send a message to B using the ElGamal encryption system. For this, A needs to know the public key of B. Thus, B uses the following steps to generate his or her private and public keys.
1. Choose a large prime number p.
2. Choose a random number q in the group G = <, that is, 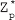 ,*>
,*>1 ≤ q < p.
3. Choose a primitive root e1 in the group G = <Zp*,*>.
4. e2: = e.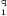 mod p
mod p
5. Announce (e1, e2, p) as the public key.
6. Retain q as the private key and keep it secret.
After knowing the public key of B, anyone can now send a message to B using its public key.
ElGamal encryption
Suppose the user A wants to send an encrypted message to B. For this, A uses the B's public key (e1, e2, p) and the following steps to convert the plaintext P to ciphertexts C1 and C2.
1. Choose a random number d in the group G = <.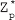 ,*>
,*>
2. C1: = e. mod p
mod p
3. C2: =(P * e.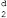 ) mod p
) mod p
4. Send C1 and C2.
ElGamal decryption
After receiving the ciphertext (C1 and C2), the recipient B uses its private key q to decrypt the ciphertext and, thus, obtain the original plaintext P, as shown here:
P =[C2(C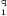 )-1] mod p
)-1] mod p
Proof of decryption
We can also verify the ElGamal decryption expression [C2(C to be equivalent to 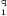 )-1] mod p
)-1] mod pP. Putting the values of C1 and C2 in the ElGamal decryption expression, we get:
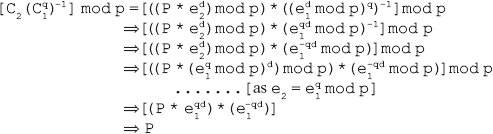
9. Discuss the different attacks on the ElGamal algorithm.
Ans.: Although the ElGamal algorithm can be used for key exchange, encryption, decryption and authentication of small messages, it has certain weaknesses that may help an attacker to crack the security of the algorithm. Generally, the ElGamal cryptosystem is subject to two types of attacks, which are as follows:
 Modulus attack: In case the value of
Modulus attack: In case the value of modulus p is small, it will be much easier for an attacker to solve the discrete logarithm problem. For example, the attacker can easily solve the discrete logarithm problem q = loge1e2 mod p and obtain the value of q. It can store the value of q and use it to decrypt any message sent to the recipient. The attacker can do so as long as the recipient uses the same keys. The attacker can also easily solve the discrete logarithm problem d = loge1C1 mod p and get the value of random number d used by the sender. Thus, to avoid this attack, it is recommended to use large values, at least of 1024 bits, for modulus p.
 Known-plaintext attack: If the sender uses the same value of
Known-plaintext attack: If the sender uses the same value of q to encrypt two different plaintexts, P1 and P2 , the attacker can determine P2 if he or she knows P1 . Let C = P1 * e and 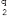 mod p
mod pC' = P2 * e. Now, the attacker can determine 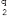 q mod p
q mod pP2 using the following steps:
1. e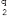 : = C' * P
: = C' * P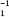 mod p
mod p
2. P2: = C' * (e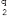 )-1 mod p
)-1 mod p
Thus, to avoid this attack, it is recommended that the sender use a different value of q to encrypt each plaintext.
10. Write a short note on elliptic curves.
Ans.: An elliptic curve can be defined by an equation in two variables with coefficients. The general form of an elliptic curve is given as:
y2 + b1xy +b2y = x3 + a1x2 +a2x +a3
Where x, y are the variables, while a1, a2, a3, b1 and b2 are the coefficients.
There are three kinds of elliptic curves, which are as follows:
 Elliptic curves over real numbers: When we talk about elliptic curves over real numbers, we use a special class of elliptic curves, of the form given here:
Elliptic curves over real numbers: When we talk about elliptic curves over real numbers, we use a special class of elliptic curves, of the form given here:
y2 = x3 + ax + b
Here, the variables x and y take values of real numbers and the coefficients a and b are the real numbers as well.
 Elliptic curves over finite field GF(p): In elliptic curves over finite field
Elliptic curves over finite field GF(p): In elliptic curves over finite field GF(p), the variables and coefficients are bound to be the elements of the finite field. Here, the elliptic curve is denoted as Ep(a,b), where p is the modulus and all calculations are made using modulo p. The elliptic curve Ep(a,b) over finite field GF(p) is represented as:
y2 mod p =(x3 + ax + b)mod p
Notice that the value of x lies between 0 and p.
 Elliptic curves over finite field
Elliptic curves over finite field GF(2n): The elliptic curves over finite field GF(2n), denoted as E2n(a,b), are of the form given here:
y2 + xy = x3 + ax2 + b
Where the variables x and y and the coefficients a and b are the elements of finite field GF(2n), and all calculations are performed in GF(2n).
11. What is the elliptic curve cryptosystem?
Ans.: The elliptic curve cryptosystem (ECC) is a public-key cryptosystem based on the theory of elliptic curves over finite field, and was unveiled by Neal Koblitz and Victor S. Miller in 1985. It involves both groups and logarithmic problems, and provides a higher rate of security at smaller key size, which is not possible using ElGamel and RSA.
In ECC, the plaintext is first encoded in the form of P(x,y) point and then further encrypted or decrypted.
ECC with Diffie-Hellman key exchange
Consider that A and B are two users who wish to communicate and, thus, exchange the secret key using ECC. The exchange of key between A and B proceeds as follows:
1. Choose a large integer p, such that p is either a prime or in the form 2n.
2. Choose the elliptic curve coefficients a and b for the cubic equations of the form y2 mod p = (x3 + ax + b)mod p or y2 + xy = x3 + ax2 + b. This defines Ep(a,b), the elliptic group of points.
3. Choose a base point G =(x1,y1) in Ep(a,b), whose order is a very large value, m.
4. A chooses an integer XA < m, which becomes his or her private key. Then, A calculates his or her public key YA, as shown here:
YA = XA * G
The public key YA is a point in Ep(a,b).
5. B chooses an integer XB < m, which becomes his or her private key. Then, B calculates his or her public key YB, as shown here:
YB = XB * G
The public key YB is a point in Ep(a,b).
6. A calculates the secret key K using his or her private key XA and the public key of B (that is, YB), as shown here:
K = XA * YB
7. Similarly, B calculates the secret key K using his or her private key XB and public key of A (that is, YA), as shown here:
K = XB * YA
Proof of algorithm
To prove that both A and B have generated the same secret key, we need to show that the calculation of K by both users yield the same result.
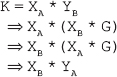
Hence, proved.
ECC encryption
When A has to send a message (say, Pm) to B, A first chooses a random integer (say, r). Then, A encrypts the message using B's public key YB and the base point G to produce the ciphertext Cm, containing the pair of points as shown here:
Cm = {r * G, Pm + r * YB}
ECC decryption
On receiving the ciphertext Cm, B decrypts the ciphertext to obtain the original plaintext Pm. For this, it multiplies the first point in Cm (that is, r * G) with its private key XB, and then subtracts it from the second point (that is, Pm + r * YB), as shown here:
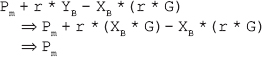
Security of ECC
A encrypts the message Pm with r * YB (r is only known to A) and r * G; therefore, the attacker needs the value of r, G and r * G to decrypt the message, which is not so easy.
12. Encrypt the plaintext 6 using RSA public key encryption algorithm. Use prime numbers 11 and 3 to compute the public key and private key. Also, decrypt the cipher text using the private key.
Ans.: According to the RSA algorithm explained in Question 2, we have:
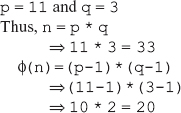
We choose D = 3 (a number relatively prime to 20, that is, gcd (20,3)= 1)
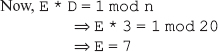
As we know, the public key consists of (E,p), and the private key consists of (D,p). Therefore, the public key is (7, 33), and the private key is (3, 33).
The plaintext 6 can be converted into ciphertext using the public key (7, 33), as shown here:

If we apply the private key to the ciphertext 30, we get the original plaintext, as follows:
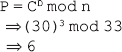
13. In the Diffie-Hellman key exchange algorithm, let the prime number be 353 and one of its primitive root be 3. Let the users A and B select their secret keys XA = 97 and XB = 233. Compute:
(i) The public keys of A and B
(ii) The common secret key
Ans.: According to the Diffie-Hellman key exchange algorithm explained in Question 5, we have:
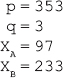
(i) Public key of A
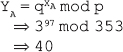
Public key of B

(ii) Common secret key
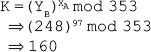
14. A is using the ElGamal encryption system to transmit a message to B, with p = 11, primitive root in G is 2, private key of A is 3 and the plaintext is 7.
(i) Calculate e2 and public key of A
(ii) If B chooses d = 4, then calculate C1, C2
Ans.: According to the ElGamal encryption system explained in Question 8, we have:

(i) As we know, e2 = e mod p
mod p

Thus, the public key of A =(e1, e2, p)=(2, 8, 11)
(ii) Given, d = 4
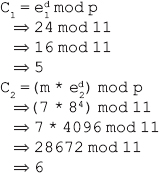
Thus, the ciphertexts are C1 = 5 and C2 = 6.
15. Using elliptic curve encryption/decryption scheme, key exchange between users A and B is accomplished. The cryptosystem parameters are elliptic group of points E11(1, 6) and point G on the elliptic curve is G = (2, 7). B's secret key is XB = 7.
(i) Find out B's public key YB.
(ii) A wishes to encrypt the message Pm = (10, 9) and chooses the random value r = 3. Determine the ciphertext Cm.
(iii) How will B recover Pm from Cm?
Ans.: Given G = (2, 7)
B's private key, XB = 7
(i) B's public key, YB, can be computed as:
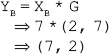
(ii) Given, Pm = (10, 9) and r = 3. Thus, the ciphertext Cm can be computed as:
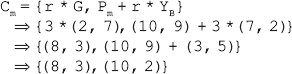
(iii) B can recover Pm from Cm using its private key (XB) as follows:
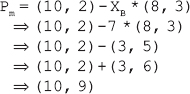
Multiple-choice Questions
1. In asymmetric-key cryptography, how many keys are required for each communicating party?
(a). 2
(b). 3
(c). 4
(d). 1
2. In asymmetric-key cryptography, the private key must be __________.
(a). Shared with anyone
(b). Distributed
(c). Kept secret
(d). None of these
3. In asymmetric-key cryptography, if A wants to communicate with B, then B must know __________.
(a). A's private key
(b). A's public key
(c). B's private key
(d). B's public key
4. If a sender encrypts the message with his or her private key, it achieves __________.
(a). Confidentiality
(b). Confidentiality and authentication
(c). Confidentiality but not authentication
(d). Authentication
5. To decrypt a message that is encrypted using RSA, we need the __________.
(a). Sender's private key
(b). Sender's public key
(c). Receiver's private key
(d). Receiver's public key
6. Which method provides a higher level of security with a small-sized key?
(a). RSA
(b). ElGamal
(c). Elliptic curve cryptography
(d). Diffie-Hellman key agreement
7. Which of the following is the first secure key exchange algorithm?
(a). RSA
(b). ElGamal
(c). Elliptic curve cryptography
(d). Diffie-Hellman key agreement
Answers
1. (a)
2. (c)
3. (b)
4. (b)
5. (c)
6. (c)
7. (d)
1. What do you mean by message authentication?
Ans.: Message authentication refers to the mechanism used to ensure that the integrity of the received message has been preserved - that the message has not been altered during transmission. It also assures the receiver that the message has originated from the intended sender and not from any intruder. Thus, a message is said to be authentic if the message has not been altered and has come from the actual sender.
2. What types of attacks are addressed by message authentication?
Ans.: The messages transmitted across a network are subject to various attacks. The types of attacks that are addressed by message authentication are as follows:
 Masquerade: This attack happens when the messages from a fraud source are put into the network; an intruder impersonates an authorized entity and creates fake messages, which are sent to the recipient. This attack also includes the fake acknowledgements corresponding to the received or failed messages by some other entity except the intended recipient.
Masquerade: This attack happens when the messages from a fraud source are put into the network; an intruder impersonates an authorized entity and creates fake messages, which are sent to the recipient. This attack also includes the fake acknowledgements corresponding to the received or failed messages by some other entity except the intended recipient.
 Modification of the message: This attack involves making certain modifications in the contents of the captured message or changing the sequence of messages being transmitted between the communicating parties. An intruder may insert, delete or transpose the contents of the message, or he or she may reorder the messages being sent in order to cause an unauthorized effect.
Modification of the message: This attack involves making certain modifications in the contents of the captured message or changing the sequence of messages being transmitted between the communicating parties. An intruder may insert, delete or transpose the contents of the message, or he or she may reorder the messages being sent in order to cause an unauthorized effect.
 Timing modification: This attack involves delaying or replaying the messages being transmitted. The term ‘replay’ means capturing a copy of the message sent by the original sender and retransmitting it later to bring about an unauthorized result. In a connection-oriented application, the entire session can be delayed or replayed, whereas in a connection-less application, the individual messages can be delayed or replayed.
Timing modification: This attack involves delaying or replaying the messages being transmitted. The term ‘replay’ means capturing a copy of the message sent by the original sender and retransmitting it later to bring about an unauthorized result. In a connection-oriented application, the entire session can be delayed or replayed, whereas in a connection-less application, the individual messages can be delayed or replayed.
3. Discuss various types of authentication functions?
Ans.: Each authentication mechanism involves the use of a function to produce a value to be used for authenticating a message. This value is known as the authenticator. The authenticator enables the recipient of the message to verify the authenticity of the message.
The authentication functions that are used to produce an authenticator fall under three classes, which are as follows:
 Message encryption: In this class, the authenticator of the message is the ciphertext that is produced after encrypting the entire plaintext.
Message encryption: In this class, the authenticator of the message is the ciphertext that is produced after encrypting the entire plaintext.
 Message authentication code (MAC): In this class, the authenticator of the message is a fixed-length value that is generated by applying a function on the message and the secret key.
Message authentication code (MAC): In this class, the authenticator of the message is a fixed-length value that is generated by applying a function on the message and the secret key.
 Hash function: In this class, a hash function (also called message digest algorithm ) is applied on a variable-length message to produce a fixed-length output that acts as the authenticator of the message.
Hash function: In this class, a hash function (also called message digest algorithm ) is applied on a variable-length message to produce a fixed-length output that acts as the authenticator of the message.
4. Write a short note on message authentication code?
Ans.: Message authentication code (MAC) is a piece of information used to authenticate a message being transmitted between two communicating parties. A MAC algorithm is applied on an arbitrary-length message to be authenticated and the common secret key shared between the parties to generate a small fixed-size block of data called cryptographic checksum (or MAC). The calculated MAC is concatenated with the original message, and the message plus MAC are then sent to the receiver.
Let A and B be two parties that share a common secret key K. When A wants to send a message (say, M) to B, it computes MAC by applying the MAC algorithm (say, C) on message M and secret key K, as shown here:
MAC = C(K, M)
After MAC has been computed, A sends the message M and MAC to B through the network. On receiving, B distinguishes the message M from MAC and applies the same MAC algorithm C on the message M and the secret key K to generate MAC'. Then, MAC' and MAC are compared to determine whether they are the same. If so, B is assured that the message M has not been altered, because if it was changed by an attacker, then MAC' would not match with MAC; the attacker cannot change MAC to correspond to the changed message, as he or she is not aware of the secret key K. In addition, B is also assured that the message M has actually come from A, since nobody else could have created a message with the proper MAC without having knowledge of the secret key K. Notice that in case the messages being transmitted between A and B also comprise sequence numbers, then B can also be assured about the proper sequence, as the attacker cannot change the sequence number successfully.
Figure 7.1 depicts the use of MAC to authenticate a message at the sender's end and to verify the authenticity of the message at the receiver's end.
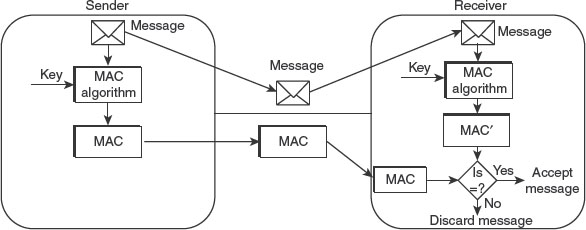
Figure 7.1 Message Authentication using MAC
MAC is different from message encryption in the sense that the MAC algorithm is not required to be reversible as it should be for decryption at the receiver's end. Generally, the MAC function is a many-to-one function whose domain comprises messages of any length, while the range comprises all possible MACs and keys. For an n-bit MAC, there are 2n possible MACs and m possible messages, where m>>2n. For a k-bit key, there are 2k possible keys. For example, if the messages being transmitted are of 100 bits and the MAC is of 10 bits, then there are 2100 different messages and 210 different MACs. Thus, it can be said that, on average, each MAC is generated by 2100/210 = 290 different messages. Furthermore, if the key used is of 10 bits, then there are 210 different mappings between all the messages and the MACs.
MAC is widely helpful in some situations, which are as follows:
 When the same message has to be broadcasted to several destinations, it would be desirable to assign to one destination the responsibility of checking the authenticity of the message. Thus, the plaintext message and the message authentication code must be sent to all the destinations. Since the responsible destination is aware of the secret key, it verifies whether the message is authentic. In case some violation occurs, it alerts other destinations.
When the same message has to be broadcasted to several destinations, it would be desirable to assign to one destination the responsibility of checking the authenticity of the message. Thus, the plaintext message and the message authentication code must be sent to all the destinations. Since the responsible destination is aware of the secret key, it verifies whether the message is authentic. In case some violation occurs, it alerts other destinations.
 When the receiving side is heavily loaded and cannot decrypt all the messages, then messages can be authenticated on a selective basis. That is, the messages are chosen randomly for verification.
When the receiving side is heavily loaded and cannot decrypt all the messages, then messages can be authenticated on a selective basis. That is, the messages are chosen randomly for verification.
 When it is more important to authenticate messages rather than keeping them secret.
When it is more important to authenticate messages rather than keeping them secret.
5. Write down the purpose of hash function along with a simple hash function.
Ans.: A hash function (or one-way hash function) is a variation of MAC used for message authentication. Like MAC, it takes a variable-length message as input and produces a fixed-length output referred to as the hash code or hash value or a message digest. However, unlike MAC, a hash function does not require a secret key and, thus, is also called a non-key message digest. Formally, the hash code (h) can be expressed as:
h = H(M)
Where,
M = message (string) of any length
H = hash function
H(M) = a fixed-length string (hash code).
At the sender's end, the hash code is computed and concatenated with the message. The message plus hash code are then sent to the receiver through the network. At the receiving end, the receiver separates the message from the hash code and again applies the hash function on it to produce a new hash code. If the recomputed hash code is the same as the received hash code, the message is authenticated.
A secret key is not given as an input to hash function. Thus, hash code plays the role of a ‘signature’ for the data being sent from the sender to the receiver through the network. In addition, the hash function takes into account all bits of the message; therefore, a change to any bit of the message results in a change to the hash code.
Simple Hash Function
All the hash functions consider the input message as a sequence of blocks where each block is of m bits. They process the input message one block at a time iteratively and produce an m-bit hash code.
One of the simple hash functions takes the bitwise XOR of every block of the input message to produce the hash code. This can be expressed as follows:
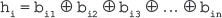
Where,
hi = ith bit of the hash code with 1 ≤ i ≤ m
n = number of m-bit blocks in the input message
bik = ith bit of the kth block with 1 ≤ k ≤ n.
The preceding operation is known as longitudinal redundancy check (LRC), and it generates a simple parity corresponding to each bit position. It effectively ensures data integrity for randomly selected input; however, it proves less effective in case of predictable formatted data. To improve the effectiveness, an alternate simple hash function is used that circular-shifts (or rotates) the hash value by one bit after processing each block. This hash function uses the following steps to produce an m-bit hash code from an input message consisting of m-bit blocks.
1. Set all the m bits of hash code to zeros.
2. For each successive m-bit block, perform the following:
i. Shift left the current value of hash code by one bit.
ii. Take the XOR of new hash code and the block.
6. What characteristics (requirements) are needed in secure hash function.
Ans.: A hash function takes as input a variable-length message, a file or any block of data and produces a hash code, referred to as the fingerprint of the message, file or block of data. If M is a variable-length message and H is the hash function, then the hash code (h) can be expressed as:
h = H(M)
The hash function must possess the following properties in order to be used for message authentication.
1. The hash function should be applicable on a block of data of any size.
2. The output produced by the hash function should always be of fixed length.
3. For any given message or block of data, it should be easier to generate the hash code. That is, given a message M, H(M) should be easily computable. This property is important to make the hardware and software implementation feasible.
4. Given a hash code, it should be nearly impossible to determine the corresponding message or block of data. That is, if h is given, one should not be able to determine M such that H(M)= h. This is referred to as one-way property. This property is of prime importance when a secret value is being used in the authentication technique. Though the secret value is not sent through the network, the attacker can still easily find out the secret value if the used hash function does not show the one-way property.
5. Given a message or block of data, it should not be computationally feasible to determine another message or block of data generating the same hash code as that of the given message or block of data. That is, if M1 is given, there is no other M2 (where M1 ≠ M2) such that H(M1)= H(M2). This property is referred to as weak collision resistance.
6. No two messages or blocks of data, even being almost similar, should be likely to have the same hash code. That is, it is virtually impossible to determine a pair (M1,M2) such that H(M1)= H(M2). This property is referred to as strong collision resistance.
From these six properties, if the first five properties are satisfied, then the hash function is called a weak hash function, and if all the six properties are satisfied, then it is called a strong hash function. This is because the sixth property protects the hash function from the birthday attack.
7. Describe the birthday attack against any hash function.
Ans.: When two different messages on applying the same hash function yield the same hash code, it is known as collision. A specific type of cryptographic attack that is performed against hash functions in order to discover collisions in them is referred to as birthday attack. This attack is based on the principle of Birthday Paradox, according to which, in a group of 23 randomly chosen people, the probability of finding two people sharing the same birthday is more than 50%. In case the number of people increases to 57, this probability becomes more than 99%. Thus, it can be concluded that the probability of finding a pair with same birthday in a group increases with increase in number of people in the group and, at a certain point, it may reach 100%.
In a birthday attack against a given hash function H, the goal of the attacker is to find two input messages, say M1 and M2, such that H(M1)= H(M2); this is what is referred to as collision. To detect the collision, the attacker may continue to evaluate the hash function H for different randomly selected inputs until he or she gets the same output more than once. In case a hash function H produces N different outputs with same probability and N is quite large, then it can be expected to get a pair of different inputs M1 and M2 such that H(M1) = H(M2) after we evaluate the function for approximately 1.25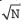 different inputs on average.
different inputs on average.
To estimate the expected number of values that we must choose before detecting the first collision, let us take q values at random from the set of N values, with repetitions allowed. Further, assume that p(q; N) denotes the probability that at least one value is chosen more than once. The approximate value of this probability can be given as shown here:
If n(p; N) denotes the least number of values that must be chosen such that the probability for detecting a collision is at least p, then we can find the approximate value of n(p; N) by inverting the preceding expression as shown here:

For 50% probability of detecting collision (that is, p = 0.5), we get
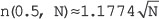
Now, the expected number of values that must be selected before detecting the first collision, denoted as Q(N), can be approximated as shown here:
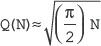
For example, if we use a 64-bit hash code, then there will be approximately 1.8 × 1019 different outputs. If all of these are equally probable (the best case), then an attacker would require approximately 5.1 × 109 attempts to generate a collision using brute force. This value is called birthday bound. In general, for an m-bit hash code, the birthday bound can be approximated as 2m/2.
8. Write a short note on iterated hash functions?
Ans.: To ensure message integrity, the hash functions are used that produce a fixed-length message digest from a variable-length message. To accomplish this efficiently, iterations are used in the hash function. In place of using hash functions with variable-length input, the hash functions with fixed-length input can also be created and used the required number of times. Such a fixed-size input hash function is termed as a compression function. This function takes as input an m-bit string and produces an n-bit string as output such that n < m. This scheme is known as iterated cryptographic hash function.
There are two different approaches that can be used in designing iterated hash functions. In the first approach, the cryptographic hash functions employ a compression function that is made from the scratch and has been designed for that specific purpose. Examples of such cryptographic hash functions include all versions of message digest (MD) algorithm such as MD2, MD4 and MD5 as well as all versions of secure hash algorithm (SHA) such as SHA-1, SHA-224, SHA-256, SHA-384 and SHA-512. On the other hand, in the second approach, the cryptographic hash functions use a symmetric-key block cipher such as triple-DES or AES as the compression function. Notice that the role of block ciphers here is to perform only encryption and not decryption. An example of a cryptographic hash function based on this approach is Whirlpool.
9. Explain MD5 algorithm with the help of a block diagram.
Ans.: MD5 (message digest, version 5) is a cryptographic hash algorithm developed by Ron Rivest in 1991. It came into existence after its four predecessors, all of which were developed by Rivest. The original hash algorithm was named MD. Then came MD2, which was quite weak. Therefore, Rivest started working on MD3. However, due to some technical deficiency, MD3 was never released. This led Rivest to the release of MD4, which too worked for a short period of time and ultimately, it was replaced by MD5. MD5 is quite fast and has been resistant to collision till now.
Figure 7.2 shows the block diagram for generating message digest using MD5. The algorithm takes a variable-length message as input and produces a fixed-length message digest. It processes the given input in blocks of 512 bits, which are again divided into 16 blocks of 32 bits each. The output obtained is a set of four blocks of 32 bits each, that is, total 128 bits.
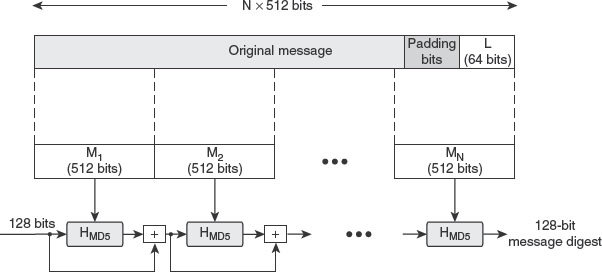
Figure 7.2 Generation of Message Digest using MD5
The following steps are involved in the working of MD5.
Step 1: Append Padding Bits
In the initial step, the padding bits are added to the end of the original message. This is done as to make the number of bits in the message equal to 64 bits less than an integral multiple of 512. For example, if the original message is of 1900 bits, then 84 bits are padded to make the length of the message 1984 bits. The reason behind adding 84 bits is that when we add 64 to 1984, we get 2048, which is an exact multiple of 512 (512*4 = 2048). Padding bits comprise a single one bit followed by the required number of zero bits. It is mandatory to add padding bits even if the length of the original message plus 64 is already an exact multiple of 512. For example, if the original message is of 448 bits (448 + 64 = 512), even then 512 padding bits need to be added. Thus, the number of padding bits may vary from 1 to 512 bits, and the length of the message after adding padding bits can be 448 bits, 960 bits, 1472 bits, and so on.
Step 2: Append Length
The next step is to calculate the length of the message excluding the padding bits. For example, if the original message is 1900 bits long, and the length of message after adding padding bits is 1984 bits, then here the length is considered as 1900 and not 1984. The length (say, L) is expressed as a 64-bit value, and these 64 bits are added at the end of the message, plus the padding bits. In case the message is too long to be expressed as a 64-bit value, then we need to take the length modulo 264. After appending the length, we get a message whose length is an exact multiple of 512. Now, the digest of this message is to be found.
Step 3: Divide the Input Message into 512-bit Blocks
In this step, the input message is divided into N 512-bit blocks, denoted as M1, M2, …, MN. For example, in our case, the 2048-bit message will be divided into four blocks of 512 bits each.
Step 4: Initialize MD Buffer
A 128-bit buffer is used to hold the intermediate and final results of the hash function while computing the message digest. This buffer is represented as four 32-bit registers (A, B, C, D). Each of these registers is initialized with a 32-bit integer in hexadecimal (initial hash values), as shown here:

The MD5 algorithm treats the registers A, B, C and D as a single 128-bit register ABCD.
Step 5: Process Blocks
Each 512-bit block of the message is now processed as follows:
a. Copy the contents of A, B, C and D into four corresponding 32-bit variables H0, H1, H2 and H3 as shown here:
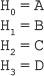
b. The 512-bit block is divided into 16 sub-blocks of 32 bits each, denoted as, S1, S2, …, S16 or in general as Si where 1 ≤ i ≤ 16.
c. Now, the compression function, labelled as HMD5 in Figure 7.2, is applied on the 512-bit block. The compression function comprises four rounds where each round takes three inputs: all the 16 32-bit sub-blocks of the current 512-bit block, the register ABCD and an array of constants T (see Figure 7.3). The array T consists of 64 elements of 32 bits each, represented as T1, T2, …, T64 or in general as Tj where 1 ≤ j ≤ 64. As there are total four rounds, 16 values of array T are used in each round. Each round updates the contents of the register ABCD by performing the MD5 algorithm steps.
d. Each round contains 16 iterations, one per each sub-block, that is, there are total 64 iterations in MD5 for one 512-bit block. Each iteration involves certain operations to update the contents of the register ABCD.
After performing all the 64 iterations for one 512-bit block, each of the four registers (A, B, C and D) is incremented by the value it had before the processing of that block, as shown here:
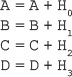
This incremented value of A, B, C and D (128 bits together) becomes one of the inputs to the first round of the next 512-bit block. Notice that addition is performed using modulo 232.
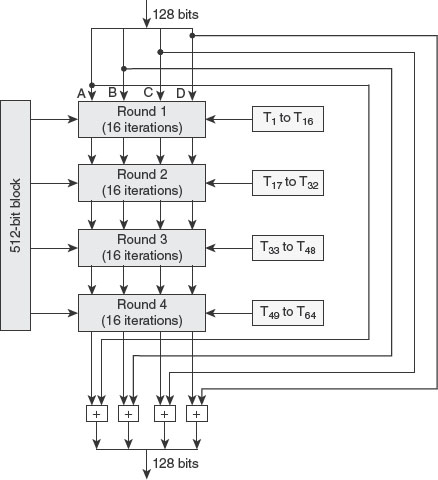
Figure 7.3 MD5 Processing of a Single 512-Block
Single MD5 Iteration: Each iteration in MD5 goes through the following steps (see Figure 7.4).
i. Apply a function F on registers B, C and D. The function F differs for each round.
ii. Add the contents of register A to the output of the previous step.
iii. Add the message sub-block Si to the output of the previous step.
iv. Add the constant Tj to the output of the previous step.
v. Perform circular left shift operation by m bits on the output of the previous step. Notice that the value of m and Tj differ for each iteration, as defined by MD5.
vi. Add the contents of register B to the output of the previous step.
vii. Store the contents of register D into a 32-bit temporary variable (say, Temp).
viii. Copy the contents of register C to register D.
ix. Copy the contents of register B to register C.
x. Copy the output of step (vi) to register B.
xi. Copy the value of variable Temp to register A.
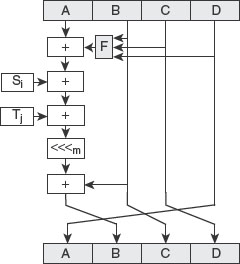
Figure 7.4 Single MD5 Iteration
After performing these steps, we get new ABCD for the next iteration.
Mathematical representation of a single MD5 iteration can be given as:
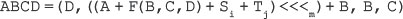
Where,
F = a non-linear function different for each round
Si = Sq x 16 + i, the ith 32-bit sub-block in the qth 512-bit block of the message
Tj = a 32-bit constant
<<<m = circular left shift by m bits
+ = addition modulo 232.
Function F: The function F is different in each of the four rounds, while the rest of the steps are the same. The function F involves some Boolean operations on the variables B, C and D in the four rounds, as shown here:

Step 6: Output
After all the 512-bit blocks of the message have been processed, the contents of the register ABCD form the 128-bit message digest.
10. Explain the working of SHA-1.
Ans.: Secure Hash Algorithm (SHA), also referred to as Secure Hash Standard (SHS), was developed by the National Security Agency (NSA). In 1993, it was published by the National Institute of Standards and Technology (NIST) as a Federal Information Processing Standard (FIPS PUB 180). In 1995, a revised version of SHA was issued as FIPS PUB 180-1, which was given the name SHA-1. SHA-1 has been designed such that it is computationally infeasible to determine the original message from a given message digest, as well as to determine two messages generating the same message digest.
Figure 7.5 shows the block diagram for generating a message digest using SHA-1. Like MD5, the SHA-1 algorithm takes an input message with a maximum length of 264 bits and processes the input in 512-bit blocks. However, it produces a message digest of 160 bits, unlike MD5.
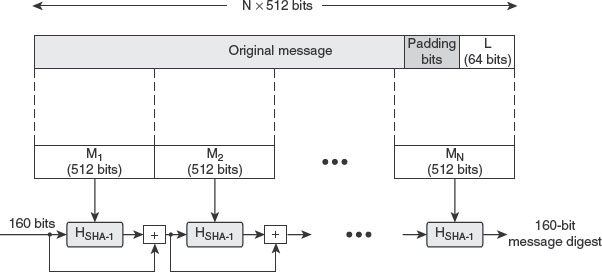
Figure 7.5 Generation of Message Digest using SHA-1
The working of SHA-1 involves the following steps:
Step 1: Append Padding Bits
In the initial step, the padding bits are added to the end of the original message. This is done as to make the number of bits in the message equal to 64 bits less than an integral multiple of 512. For example, if the original message is of 1900 bits, then 84 bits are padded to make the length of the message 1984 bits. The reason behind adding 84 bits is that when we add 64 to 1984, we get 2048, which is an exact multiple of 512 (512*4 = 2048). Padding bits comprise a single one bit followed by the required number of zero bits. It is mandatory to add padding bits even if the length of the original message plus 64 is already an exact multiple of 512. For example, if the original message is of 448 bits (448 + 64 = 512), even then 512 padding bits need to be added. Thus, the number of padding bits may vary from 1 to 512 bits, and the length of the message after adding padding bits can be 448 bits, 960 bits, 1472 bits and so on.
Step 2: Append Length
The next step is to calculate the length of message excluding the padding bits. For example, if the original message is 1900 bits long, and the length of message after adding the padding bits is 1984 bits, then here the length is considered as 1900 and not 1984. The length (say, L) is expressed as a 64-bit value, and these 64 bits are added at the end of the message plus padding bits. In case the message is too long to be expressed as a 64-bit value, then we need to take the length modulo 264. After appending the length, we get a message whose length is an exact multiple of 512. Now, the digest of this message is to be found.
Step 3: Divide the Input Message into 512-bit Blocks
In this step, the input message is divided into N 512-bit blocks, denoted as M1, M2, …, MN. For example, in our case, the 2048-bit message will be divided into four blocks of 512 bits each.
Step 4: Initialize Hash Buffer
A 160-bit buffer is used to hold the intermediate and final results of the hash function while computing the message digest. This buffer is represented as five 32-bit registers (A, B, C, D, E). Each of these registers is initialized with a 32-bit integer in hexadecimal (initial hash values), as shown here:

The SHA-1 algorithm treats the registers A, B, C, D and E as a single 160-bit register ABCDE.
Step 5: Process Blocks
Each 512-bit block of message is now processed. Initially, the contents of the five registers A, B, C, D and E are copied to five 32-bit variables H0, H1, H2, H3 and H4, respectively. Then, the 512-bit block is divided into 16 sub-blocks of 32 bits each. Now, the compression function, labelled as HSHA-1 in Figure 7.5 , is applied on the 512-bit block. The compression function consists of four rounds, with each round consisting of 20 iterations. That is, a total of 80 iterations are performed to process one 512-block. As shown in Figure 7.6 , each of the four rounds takes three inputs: all the 16 32-bit
sub-blocks of the current 512-bit block, the register ABCDE and an additive constant Ti where 1 ≤ i ≤ 80. Unlike MD5, in SHA-1, we have only four values defined for Ti, one value per round, as shown in Table 7.1.
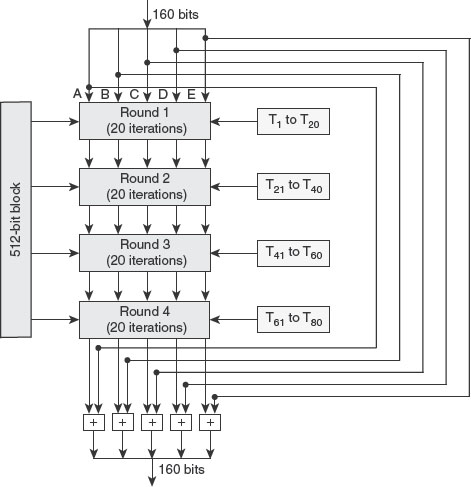
Figure 7.6 SHA-1 Processing of a Single 512-bit Block
| Round | Value of i | Value of Ti (in hexadecimal) |
|---|---|---|
1 |
1 ≤ i ≤ 20 |
5A 92 79 99 |
2 |
21 ≤ i ≤ 40 |
6E D9 EB A1 |
3 |
41 ≤ i ≤ 60 |
F8 1B BC DC |
4 |
61 ≤ i ≤ 80 |
CA 62 C1 D6 |
Each iteration of SHA-1 involves certain operations to update the contents of the register ABCDE. After performing all the 80 iterations for one 512-bit block, each of the five registers (A, B, C, D and E) is incremented by the value it had before the processing of that block, as shown here:
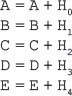
This incremented value of A, B, C, D and E (160 bits together) becomes one of the inputs to the first round of next 512-bit block. Notice that addition is performed using modulo 232.
Single SHA-1 Iteration: Each iteration in SHA-1 goes through the following steps (see Figure 7.7).
i. Apply a function F on registers B, C and D. The function F differs for each round.
ii. Add the contents of register E to the output of the previous step.
iii. Store the contents of register A into a 32-bit temporary variable (say, Temp).
iv. Perform circular left shift operation by five bits on the contents of register A.
v. Add the output of step (ii) and step (iv).
vi. Derive Wi from the current sub-block and add it to the output of the previous step.
vii. Add the constant Ti to the output of the previous step.
viii. Copy the contents of register D to register E.
ix. Copy the contents of register C to register D.
x. Perform circular left shift operation by 30 bits on the contents of register B and store the result in register C.
xi. Copy the value of variable Temp to register B.
xii. Copy the output of step (vii) to register A.
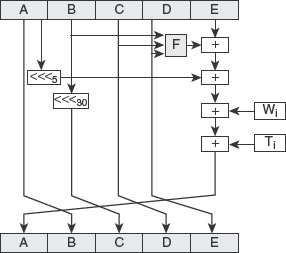
Figure 7.7 Single SHA-1 Iteration
After performing the preceding steps, we get new ABCDE for the next iteration.
Mathematical representation of a single SHA-1 operation can be given as:
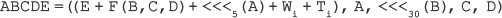
Where,
F = a non-linear function different for each round
Wi = a 32-bit block derived from current 32-bit sub-block Si based on rules (see Table 7.2)
Ti = one of the five 32-bit additive constants
<<<m = circular left shift by m positions
+ = addition modulo 232.
| Value of i | Value of Wi |
|---|---|
1 ≤ i ≤ 16 |
Same as Mi |
17 ≤ i ≤ 80 |
|
Function F: The function F is different in each of the four rounds, while the rest of the steps are the same. The function F involves some Boolean operations on the variables B, C and D in the four rounds, as shown here:
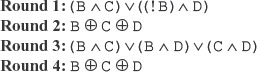
Step 6: Output
After all the 512-bit blocks of the message have been processed, the contents of the register ABCDE form the 160-bit message digest.
11. Differentiate between SHA-1 and MD5.
Ans.: Both SHA-1 and MD5 are message digest algorithms. The design and functionality of SHA-1 and MD5 are almost similar. However, there are certain key differences between them. Some of these differences are listed in the Table 7.3.
| SHA-1 Algorithm | MD5 Algorithm |
|---|---|
| It generates a message digest of 160 bits. | It generates a message digest of 128 bits. |
| It uses little-endian scheme to interpret the message as a sequence of 32-bit words. In this scheme, the most significant byte of a 32-bit word is stored in the low-address byte position. | It uses big-endian scheme, where the least significant byte of a 32-bit word is stored in the low-address byte position. |
| It undergoes four rounds, each having 20 iterations, that is, a total of 80 iterations are used. Moreover, it requires a 160-bit buffer and, thus, is slower in operation than MD5. | It undergoes four rounds, each having 16 iterations, that is, a total of 64 iterations are used. Moreover, it requires a 128-bit buffer and, thus, is faster in operation than SHA-1. |
| It requires 2160 operations for finding the original message from the given message digest and 280 operations to find two messages generating the same message digest. | It requires 2128 operations for finding the original message from the given message digest and 264 operations to find two messages generating the same message digest. |
| It is not vulnerable to cryptanalytic attack. | It is vulnerable to cryptanalytic attack. |
| It is more secure than MD5. | It is less secure as compared to SHA-1. |
12. Explain Whirlpool cryptographic hash function.
Ans.: Whirlpool is a cryptographic hash function designed by Vincent Rijmen and Paulo S.L.M. Barreto. It is one of the hash functions that have been supported by New European Schemes for Signatures, Integrity, and Encryption (NESSIE). It is based on the use of a symmetric-key block cipher instead of a compression function as used in MD5 and SHA. The Whirlpool cipher is a modified version of the Advanced Encryption Standard (AES) cipher.
Whirlpool Hash Function
Figure 7.8 shows the block diagram for generating a message digest using Whirlpool (the triangular hatch in the figure indicates key input). The algorithm takes as input a message with a maximum length of up to 2256 bits, processes the input in 512-bit blocks and returns a 512-bit hash code as output. The steps involved in the working of the Whirlpool hash function are as follows:
1. Append padding bits: In the initial step, the padding bits are added to the end of the original message. This is done so as to make the length of the message an odd multiple of 256. For example, if the original message is of 600 bits, then 168 bits are padded to make the length of the message 768 bits (768 = 256*3). Padding bits comprise a single one bit followed by the required number of zero bits. It is mandatory to add padding bits even if the length of the original message is already of the desired length. For example, if the original message is of 256 bits, even then 512 padding bits need to be added to make the length equal to 768 bits. Thus, the number of padding bits may vary from 1 to 512 bits.
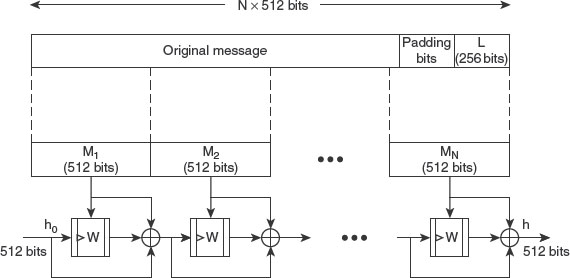
Figure 7.8 Message Digest Generation using Whirlpool
2. Append length: The next step is to calculate the length of the message excluding the padding bits. The length (say, L) is expressed as a 256-bit value, and these 256 bits are added at the end of the message plus padding bits. After appending the length, we get a message whose length is an even multiple of 256 or an integral multiple of 512.
3. Divide the message into 512-bit blocks: The message is divided into N 512-bit blocks, M1, M2, …, MN. Each of these blocks is treated as an array of 8-bit bytes (that is, total 64 bytes). A byte matrix of size 8 × 8 is used to hold the intermediate and final hash values. The matrix is initialized with zero bits.
4. Process message blocks: Each message block of 512 bits is processed through the Whirlpool cipher (W) and, finally, a 512-bit message digest (h) is generated. To process the first message block, the 512-bit message digest (h0) is initialized with all zeros and is used as the cipher key for encrypting the first message block. The ciphertext produced after encrypting each block is XORed with the previous cipher key and previous plaintext block. The result obtained is used as the cipher key for encrypting the next 512-bit block. This process continues, and the final ciphertext block after the last XOR operation becomes the final 512-bit message digest h.
Whirlpool Cipher
The Whirlpool cipher (W) is a non-Feistel cipher that operates on 512-bit blocks (64 bytes). It consists of 10 rounds and uses a key size of 512 bits. The cipher uses a total of 11 round keys (K0, K1, …, K10), with each key of 512 bits. The round keys are generated using the key expansion algorithm. The general design of the Whirlpool cipher is shown in Figure 7.9.
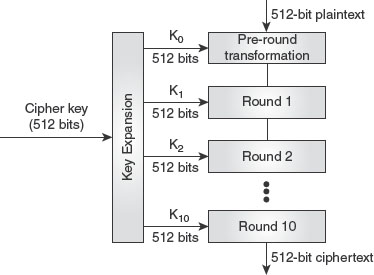
Figure 7.9 General Design of Whirlpool Cipher
State and blocks: Each round in the Whirlpool cipher consists of many stages, where each stage transforms the 512-bit (64-byte) data block. As with AES, the Whirlpool cipher also uses the term ‘block’ at the beginning and end of the cipher and the term ‘state’ before and after each stage. The only difference is that here the size of state and block is 512 bits. Each 512-bit block is treated as a row matrix of 64 bytes, and a state is treated as a square matrix of 8 × 8 bytes. The transformation from block to state and vice versa is performed row wise, unlike in AES cipher.
Structure of each round: Each round involves four transformations; namely, Substitute Bytes, Shift Columns, Mix Rows and Add Round Key (see Figure 7.10). Moreover, one Add Round Key transformation is applied before the first round (mentioned as pre-round transformation in Figure 7.9). Each transformation accepts a state, changes it and creates a new state, which is given as input to the next transformation or the next round.
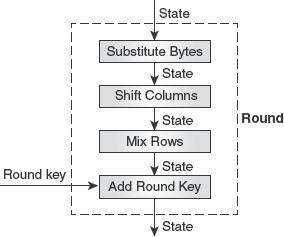
Figure 7.10 Structure of each Round in Whirlpool Cipher
The transformations involved in each round are described as follows:
 Substitute Bytes: This is the first transformation of a round that performs substitution of bytes. The input to this transformation is an 8 × 8 byte state matrix. The bytes in the matrix are substituted one at a time; thus, there are 64 distinct byte-to-byte transformations. The bytes are substituted either with the help of a substitution table or by performing the mathematical calculations in
Substitute Bytes: This is the first transformation of a round that performs substitution of bytes. The input to this transformation is an 8 × 8 byte state matrix. The bytes in the matrix are substituted one at a time; thus, there are 64 distinct byte-to-byte transformations. The bytes are substituted either with the help of a substitution table or by performing the mathematical calculations in GF(24) field. To substitute the bytes using a substitution table, each byte is treated as two hexadecimal digits, where the first digit (left one) specifies the row and the second digit (right one) specifies the column of the substitution table. The value (two hexadecimal digits) at the intersection of the row and the column in the substitution table is the new byte with which the given byte is to be replaced. Notice that, in this transformation, the contents of each byte is changed; however, the order of bytes in the matrix does not change.
 Shift Columns: This transformation performs the byte-level permutation. It is similar to Shift Rows transformation of AES with the only difference that, here, the columns of the matrix are shifted, and not the rows. The bytes in the columns of the input state matrix are shifted to the left and the number of the bytes to be shifted depends on the column number. For example, the column 0 is not shifted at all, the column 1 is shifted one byte, column 2 is shifted two bytes, and so on.
Shift Columns: This transformation performs the byte-level permutation. It is similar to Shift Rows transformation of AES with the only difference that, here, the columns of the matrix are shifted, and not the rows. The bytes in the columns of the input state matrix are shifted to the left and the number of the bytes to be shifted depends on the column number. For example, the column 0 is not shifted at all, the column 1 is shifted one byte, column 2 is shifted two bytes, and so on.
 Mix Rows: This is a matrix transformation that diffuses the bits inside the bytes of the state matrix. It takes one row of input state matrix at a time and transforms it to a new row. For transforming the rows, a constant square matrix is used whose each row is the circular right shift of its previous row. The square matrix is multiplied by each row of the state matrix, resulting in another row. Notice that the bytes multiplication operation is performed in the
Mix Rows: This is a matrix transformation that diffuses the bits inside the bytes of the state matrix. It takes one row of input state matrix at a time and transforms it to a new row. For transforming the rows, a constant square matrix is used whose each row is the circular right shift of its previous row. The square matrix is multiplied by each row of the state matrix, resulting in another row. Notice that the bytes multiplication operation is performed in the GF(28) field, and the bytes addition operation is performed by simply XORing the bits within bytes.
 Add Round Key: This is the only transformation that makes use of the round key. To perform this transformation, the 512-bit round key is considered as an 8 × 8 state matrix. Each byte of the input state matrix is added with the corresponding byte of round key state matrix in the GF(28 ) field, resulting in a new byte.
Add Round Key: This is the only transformation that makes use of the round key. To perform this transformation, the 512-bit round key is considered as an 8 × 8 state matrix. Each byte of the input state matrix is added with the corresponding byte of round key state matrix in the GF(28 ) field, resulting in a new byte.
13. What is HMAC? What are its design objectives? Explain its working.
Ans.: Hash-based MAC (HMAC) is a message authentication code derived from a cryptographic hash function such as MD5 and SHA-1. The basic idea behind HMAC is to use a secret key in the existing message digest algorithms (hash functions). It has been issued as a standard (FIPS 198) by NIST. As algorithms such as MD5 and SHA-1 do not rely on the secret key, HMAC has been selected as mandatory-to-implement MAC for IP security. It is also used in other Internet protocols, such as Secure Socket Layer (SSL).
HMAC can work with any existing message digest algorithms (hash functions). It considers the message digest produced by the embedded hash function as a black box. It then uses the shared symmetric key to encrypt the message digest, thus, producing the final output, that is, MAC.
Design Objectives of HMAC
HMAC was issued as RFC 2104, which defines the following objectives for HMAC.
 To use the existing hash functions such as MD5 and SHA-1 without modification.
To use the existing hash functions such as MD5 and SHA-1 without modification.
 To be able to easily replace an existing hash function in case a fast hash function is available or needed.
To be able to easily replace an existing hash function in case a fast hash function is available or needed.
 To maintain the original performance of the function till the time it is possible.
To maintain the original performance of the function till the time it is possible.
 To use the keys and to handle them in a simple and efficient manner.
To use the keys and to handle them in a simple and efficient manner.
 To better understand the cryptographic analysis of the strength of the authentication mechanism used in embedded hash function.
To better understand the cryptographic analysis of the strength of the authentication mechanism used in embedded hash function.
HMAC Implementation
The implementation of HMAC is very complex. Before discussing the algorithm, let us define the variables used in the algorithm.
H = embedded cryptographic hash function such as MD5 or SHA
IV = initial value to the hash function
M = input message
q = number of input blocks in M
n = length of the message digest (or hash value)
b = number of bits in a block
Mi = ith block of input message with 1 ≤ i ≤ q
K = shared symmetric key (secret key)
Kpad = secret key K padded with 0s on the left to make the length b bits
Ipad = input pad, a constant having value 00110110 (36 in hex) repeated b/8 times
Opad = output pad, a constant having value 01011100 (5C in hex) repeated b/8 times
Mathematically, the HMAC operation can be expressed as:
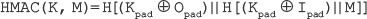
Figure 7.11 depicts the HMAC operation. Initially, the given input message M is divided into q blocks, M1, M2, …, Mq, with each block having b bits. Then, the following steps are performed to produce the n-bit message digest.
1. Add padding bits to secret key K: Add the required number of zeros to the left of secret key K to make it a b-bit string, Kpad. It is recommended that the original size of secret key K should not be greater than n, the length of the message digest.
2. XOR Kpad with Ipad : Apply XOR operation on b-bit Kpad obtained from the previous step and the constant Ipad to create a b-bit block, say S1.
3. Append M to S1 : Append the input message M (equivalent to q b-bit blocks) to the output of the previous step, that is, S1. The result is q+1 blocks of b bits each.
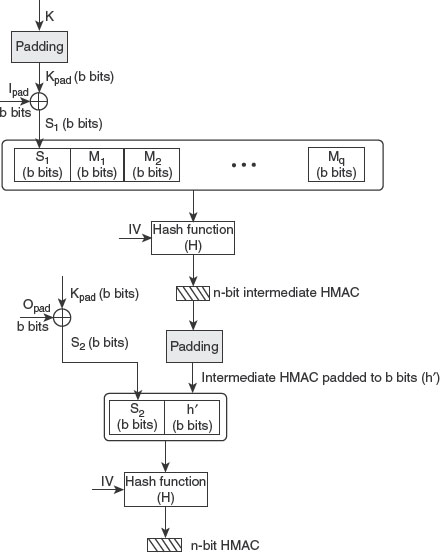
Figure 7.11 HMAC Structure
4. Apply hash function: Apply the selected hash function H on the stream containing q+1 blocks, generated in the previous step, to produce n-bit digest, referred to as the intermediate HMAC. The n-bit IV is also given as input to the hash function.
5. Add padding bits to intermediate HMAC: Add the required number of zeros to the left of n-bit intermediate HMAC to produce h′ with length equal to b bits.
6. XOR Kpad with Opad: Apply XOR operation on b-bit Kpad and the constant Opad to create a b-bit block, say S2.
7. Append h′ to S2: Append the b-bit intermediate HMAC (h′) obtained from step 5 to the output of the previous step, that is, S2.
8. Apply hash function: Apply the same hash function H with an n-bit IV as input on the output of the previous step to produce a final n-bit message digest.
14. Discuss the security of HMAC.
Ans.: The security of HMAC depends on the cryptographic strength of the embedded hash function, the size of secret key used and the length of the message digest produced. In essence, the probability of attacking HMAC successfully is equal to either of the following attacks on the embedded hash function.
 The intruder can calculate the output of compression function without having the knowledge of
The intruder can calculate the output of compression function without having the knowledge of IV, which is selected at random and kept secret.
 The intruder determines the collisions in the hash function even if the I V is secret and random.
The intruder determines the collisions in the hash function even if the I V is secret and random.
To attempt the first attack, the compression function can be viewed as a hash function that is applied on a message containing only one b-bit block. The intruder selects a random value of n bits (i.e. the length of the message digest produced) and uses it in place of IV. However, to perform this attack on the hash function, either a brute-force attack on the secret key or a birthday attack is to be attempted, because HMAC involves the secret key also while computing the hash value. Attempting a brute-force attack on the secret key requires the intruder to perform 2n operations.
On the other hand, to attempt the second attack, the intruder needs to determine two messages, M1 and M2, such that when the hash function H is applied on them, they yield the same output, that is, H(M1)=H(M2). This is the birthday attack, and it requires the intruder to perform 2n/2 operations in case the hash code is of n bits. For example, if the MD5 algorithm, which produces 128-bit hash code, is used as the embedded hash function, the intruder has to perform 264 operations in order to attempt birthday attack on the hash function. Performing so many operations does not seem infeasible with today's technology. However, it does not necessarily mean that MD5 is unsuitable to HMAC. The reason behind this is explained in the following text.
The intruder can attack MD5 by selecting some set of messages and generating the corresponding hash codes to determine the collisions. As the intruder knows the hash function as well as the default IV to MD5, he or she is able to work offline on some dedicated computing facility. However, when MD5 is used in HMAC, the intruder cannot determine the messages and their corresponding hash codes offline. This is because HMAC also involves the use of a secret key that is not known to the intruder. Therefore, the intruder needs to observe a series of messages being generated by HMAC using the same key and then attempt to attack these known messages. For a 128-bit hash code in MD5, this requires observing 264 blocks generated using the same key. To observe so many blocks on a 1-Gbps link, one would need approx 1,50,000 years to succeed. Thus, the use of MD5 is acceptable to HMAC as far as speed is concerned.
Multiple-choice Questions
1. A _________ is used to verify the integrity and authenticity of a message.
(a) Decryption algorithm
(b) Message digest
(c) MAC
(d) Both (b) and (c)
2. Which of the following is the latest version of the SHA algorithm?
(a) SHA-512
(b) SHA-256
(c) SHA-128
(d) SHA-1
3. The purpose of hash function is to ensure _________.
(a) Message integrity
(b) Message authentication
(c) Both (a) and (b)
(d) None of these
4. Choose the odd one out.
(a) RC5
(b) Blowfish
(c) ECC
(d) MAC
5. When two different messages yield the same message digest, it is called _________.
(a) Attack
(b) Collision
(c) Hash
(d) None of these
6. Which of the following is based on the use of asymmetric-key block cipher?
(a) SHA-1
(b) MD5
(c) RIPEMD
(d) Whirlpool
7. An attacker needs to perform _________ operations in order to determine collision in SHA-1.
(a) 264
(b) 280
(c) 2256
(d) 272
Answers
1. (c)
2. (a)
3. (a)
4. (d)
5. (b)
6. (d)
7. (b)
1. What is digital signature? Discuss the various services it provides.
Ans.: A digital signature is an authentication mechanism that allows the sender to attach an electronic code with the message in order to ensure its authenticity and integrity. This electronic code acts as the signature of the sender and, hence, is named digital signature. Digital signatures use the public-key cryptography technique. The sender uses his or her private key and a signing algorithm to create a digital signature, and the signed document can be made public. The receiver, on the other hand, uses the public key of the sender and a verifying algorithm to verify the digital signature.
Digital signatures are analogous to physical handwritten signatures and provide the following security services.
 Message authentication: A normal message authentication scheme protects the two communicating parties against attacks from a third party (intruder). However, a secure digital signature scheme protects the two parties against each other also. Suppose
Message authentication: A normal message authentication scheme protects the two communicating parties against attacks from a third party (intruder). However, a secure digital signature scheme protects the two parties against each other also. Suppose A wants to send a signed message (message with A's digital signature) to B through a network. For this, A encrypts the message using his or her private key, which results in a signed message. The signed message is then sent through the network to B. Now, B attempts to decrypt the received message using A's public key in order to verify that the received message has really come from A. If the message gets decrypted, B can believe that the message is from A. However, if the message or the digital signature has been modified during transmission, it cannot be decrypted using A's public key. From this, B can conclude that either the message transmission has tampered with, or that the message has not been generated by A.
 Message integrity: Digital signatures also provide message integrity. If a message bears a digital signature, then any change in the message after the signature is attached will invalidate the signature. That is, it is not possible to get the same signature if the message is changed. Moreover, there is no efficient way to modify a message and its signature such that a new message with
a valid signature is produced. These days, a hash function is used in the signing and verifying algorithms that help in preserving the integrity of the message.
Message integrity: Digital signatures also provide message integrity. If a message bears a digital signature, then any change in the message after the signature is attached will invalidate the signature. That is, it is not possible to get the same signature if the message is changed. Moreover, there is no efficient way to modify a message and its signature such that a new message with
a valid signature is produced. These days, a hash function is used in the signing and verifying algorithms that help in preserving the integrity of the message.
 Nonrepudiation: Digital signatures also ensure nonrepudiation. For example, if
Nonrepudiation: Digital signatures also ensure nonrepudiation. For example, if A has sent a signed message to B, then in future A cannot deny about the sending of the message. B can keep a copy of the message along with A's signature. In case A denies, B can use A's public key to generate the original message. If the newly created message is the same as that initially sent by A, it is proved that the message has been sent by A only. In the same way, B can never create a forged message bearing A's digital signature, because only A can create his or her digital signatures with the help of that private key.
 Message confidentiality: Digital signatures do not provide message confidentiality, because anyone knowing the sender's public key can decrypt the message. Thus, to achieve message confidentiality, we need to encrypt the message along with the signature using either the secret-key encryption or public-key encryption scheme. For example, if we use the public-key encryption scheme, then at
Message confidentiality: Digital signatures do not provide message confidentiality, because anyone knowing the sender's public key can decrypt the message. Thus, to achieve message confidentiality, we need to encrypt the message along with the signature using either the secret-key encryption or public-key encryption scheme. For example, if we use the public-key encryption scheme, then at A's end, first the message is encrypted using A's private key and then a second encryption is performed using the B's public key. Similarly, at B's end, first the message is decrypted using B's private key and then a second decryption is performed using A's public key. With this mechanism, only B can decrypt the encrypted message received from A because only B knows his or her private key.
2. Describe the digital signature process with the help of a suitable diagram.
Ans.: The digital signature process is shown in Figure 8.1. Suppose user A wants to send a signed message to B through a network. To achieve this communication, these steps are followed:
(i) A uses his private key (EA), applied to a signing algorithm, to sign the message (M).
(ii) The message (M) along with A's digital signature (S) is sent to B.
(iii) On receiving the message (M) and the signature (S), B uses A's public key (DA), applied to the verifying algorithm, to verify the authenticity of the message. If the message is authentic, B accepts the message; otherwise it is rejected.
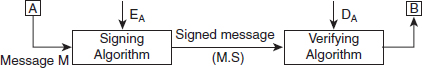
Figure 8.1 Digital Signature Process
3. How is the use of private and public keys in digital signatures different from that in public-key cryptography?
Ans.: The private and public keys used in public-key cryptography are different from the private and public keys used in digital signatures. In the former case, the public and private keys of the receiver are used for encryption and decryption of the message, respectively. That is, the sender encrypts the message using the receiver's public key, and the receiver decrypts the message using his own private key. However, in digital signatures, the private and public keys of the sender are used to create and verify the digital signature, respectively. That is, the sender creates a digital signature using his or her own private key, and the receiver verifies it using the sender's public key.
4. Can we use a secret (symmetric) key in the digital signature process? Justify your answer.
Ans.: We cannot use a secret (symmetric) key to create and verify digital signatures, due to the following two reasons.
 In symmetric-key cryptosystem, a secret key
In symmetric-key cryptosystem, a secret key K is shared between two users only, say A and B. Now, if A wants to send another message to C, then he or she has to use another secret key.

B could create a forged signed message using the secret key K that is shared between A and B, and send that message to C pretending that it has come from A.
5. What are the essential properties and requirements for a digital signature?
Ans.: A digital signature is used in those situations where there is a lack of trust between the sender and the receiver. For example, suppose a user A transfers funds to B electronically. Now, B in future increases the amount of funds transferred and claims that the larger amount had arrived from A. Thus, to achieve secure communication between the two users and to resolve their disputes if any, digital signature must have the following properties:
 It must be able to verify the author and the date and time of the signature.
It must be able to verify the author and the date and time of the signature.
 It must be able to authenticate the contents of the message at the time of the signature.
It must be able to authenticate the contents of the message at the time of the signature.
 There must be some third (trusted) party who can verify the digital signature to resolve disputes between the sender and receiver.
There must be some third (trusted) party who can verify the digital signature to resolve disputes between the sender and receiver.
Thus, we can say that the authentication function is included within the digital signature function. Based on the these properties, we can list out the following requirements for a digital signature:
 The signature must be in the form of a bit pattern and relative to the message being signed.
The signature must be in the form of a bit pattern and relative to the message being signed.
 The signature must contain some information that is unique to the sender, so that forgery and denial can be avoided.
The signature must contain some information that is unique to the sender, so that forgery and denial can be avoided.
 The process of creating the digital signature must be comparatively easy.
The process of creating the digital signature must be comparatively easy.
 The process of recognizing and verifying the digital signature must also be comparatively easy.
The process of recognizing and verifying the digital signature must also be comparatively easy.
 A high computational effort must be required to forge a digital signature. That is, it must be infeasible for an intruder to create a new message for an existing signature or to create a fake digital signature for an existing message.
A high computational effort must be required to forge a digital signature. That is, it must be infeasible for an intruder to create a new message for an existing signature or to create a fake digital signature for an existing message.
 The copy of a digital signature must be retained in some storage mechanism.
The copy of a digital signature must be retained in some storage mechanism.
6. Discuss the different kinds of attacks on digital signatures.
Ans.: There are three kinds of attacks possible on digital signatures, namely, key-only, known message and chosen-message attack. To get an idea of these attacks, consider A and B as the communicating parties and C as the opponent.
 Key-only attack: In this type of attack, the intruder knows only the public information of
Key-only attack: In this type of attack, the intruder knows only the public information of A. With the help of this information, the intruder tries to create A's digital signature. He then forges the message by putting the newly created A's signature and sends the signed message to B pretending that it has come from A. It is similar to the ciphertext-only attack discussed in Chapter 2.
 Known-message attack: In this type of attack, the intruder has access to some messages signed by
Known-message attack: In this type of attack, the intruder has access to some messages signed by A. That is, he or she already has one or more message–signature pairs. With the help of these known message–signature pairs, the intruder tries to create another message and forge A's digital signature on it. This attack is similar to the known-plaintext attack discussed in Chapter 2.
 Chosen-message attack: In this type of attack, the intruder manages to let
Chosen-message attack: In this type of attack, the intruder manages to let A sign one or more messages for him. In other words, the intruder himself chooses a message–signature pair.
Later, he creates a new message with the contents he or she wants and forges A's digital signature on it, and sends it to B pretending that it has come from A. This attack is similar to the chosen-plaintext attack discussed in Chapter 2.
7. Discuss the different approaches proposed for the digital signature function.
Ans.: A digital signature cannot be a constant and must be a function of the entire document it signs. There are several approaches that have been proposed for the digital signature function. These approaches are categorized into two types: direct and arbitrated.
Direct digital signature
In the direct digital signature approach, the signed document is directly passed from the sender to the receiver. That is, no third party is involved in carrying out this communication, because it is assumed that the receiver knows the public key of the sender and, hence, can easily verify the authenticity of the message. There are two ways of creating a digital signature—one, by encrypting the whole message with the sender's private key, and another, by taking the hash of the message and then encrypting it with the sender's private key. Message confidentiality can be achieved by further encrypting the message and the signature with the receiver's public key in case of public-key encryption or shared key in case of symmetric-key encryption.
Though there is no third party directly involved in carrying out the communication between the sender and receiver, in case of disputes, the third party may be involved in resolving the conflicts. The third party views both the message and its signature. If the signature function is applied on the encrypted message, then the third party also needs to know the decryption key to read the plaintext message. However, if the signature function is applied on the plaintext message, then the recipient can simply store the plaintext message and its signature, so that it can be used in future for resolving disputes. Thus, it is better to apply the digital signature function on the message before encrypting it.
The main problem with the direct digital signature scheme is that if the sender wants to deny the sending of a particular message, he or she can claim that his or her private key is stolen or lost and that someone has forged the signatures. Since no trusted third party is directly involved in the communication, it is difficult to verify whether the key was actually stolen, or if the sender is lying. This type of threat can be controlled to some extent by two ways:
 The sender whose key has been stolen can immediately report to a central authority, or
The sender whose key has been stolen can immediately report to a central authority, or
 The sender can include a timestamp (date and time) in each signed message.
The sender can include a timestamp (date and time) in each signed message.
The latter solution can still be compromised. For example, if the private key of the sender A is actually stolen at time (t), then some intruder (say, X) can create A's signature and send a forged signed message to B including a timestamp before or equal to t.
Arbitrated digital signature
In the arbitrated digital signature approach, a third party known as the trusted arbiter is directly involved in the process. Every signed message sent by the sender to the receiver goes through the arbiter. The arbiter performs two functions. First, it verifies the integrity (origin and content) of the signed message and signature by applying a certain number of tests. Second, it attaches the date and time of creation of the message, and forwards the message to its final destination. This scheme is based on the assumption that both the sender and receiver completely trust the arbiter's claim that he or she verifies the message to the level of his or her satisfaction and will not alter the data in any way.
The main advantages of the arbitrated digital signature approach are as follows:
 Both the communicating parties cannot share any kind of information before communication, thus preventing the chances of any kind of fraud.
Both the communicating parties cannot share any kind of information before communication, thus preventing the chances of any kind of fraud.
 Any incorrectly dated message cannot be sent to the receiver.
Any incorrectly dated message cannot be sent to the receiver.
 The contents of the message from
The contents of the message from A to B are hidden from the trusted third party and others.
8. Write a short note on the RSA digital signature scheme.
Ans.: In addition to the encryption and decryption of a message, the RSA approach can also be used for signing and verifying the message. In this case, it is known as the RSA digital signature scheme. At the sender's end, the message M to be signed is given as input to a function, which produces the digital signature S with the help of sender's private key. The sender then transmits both the message and the signature to the receiver. At the receiver's end, the digital signature S is given as input to a function, which computes the copy of the message (M′) with the help of sender's public key. Now, the receiver compares the received and the computed message. If M and M′ are congruent, the receiver accepts the message, otherwise rejects it. The RSA digital signature scheme is shown in Figure 8.2.
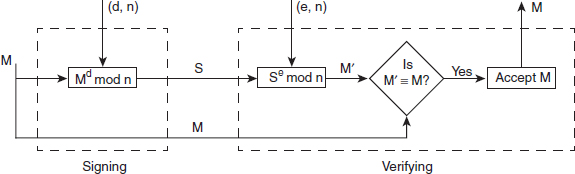
Figure 8.2 RSA Digital Signature Scheme
The key generation, signing and verifying algorithms for the RSA digital signature scheme are described as follows:
Key generation: The sender generates his or her private and public key as follows:
(i) The sender chooses two prime numbers p and q and computes the following:
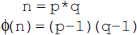
(ii) He then chooses e(1 < e < Φ(n)), the public exponent, and computes his private key d such that:
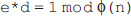
Signing: The sender creates his digital signature S using his private key d as follows:
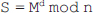
where M is the message to be signed.
Verifying: The receiver receives the message M and signature S, and computes a copy of the message using the sender's public key (e, n) as follows:
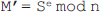
The receiver then compares M′ with M. If M′ ≡ M, the message is accepted; otherwise, it is rejected.
To prove the RSA digital signature scheme, we need to show that M′ ≡ M(mod n).
As,

And,
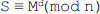
Thus, we can write equation (1) as

Hence, proved.
RSA digital signature scheme on a message digest
The RSA digital signature scheme can also be applied on a message digest. In this case, a strong hash function h is applied on the message M to create the message digest D, which is then encrypted with the sender's private key to form the digital signature S. The sender sends the message M and the signature S to the receiver. At the receiver's end, the same hash function h is applied to the received message M to compute D. The receiver also decrypts the received digital signature S with the help of the sender's public key to produce D′. Now, the receiver compares D and D′, if D is congruent to D′, the message is accepted; otherwise it is rejected.
9. Explain ElGamal digital signature scheme.
Ans.: The ElGamal digital signature scheme also consists of three different components, namely, key generation, signing and verifying. All the three components use separate algorithms. In this scheme, four functions are used, in which one function is common in both the signing and verification process, however, with different inputs. Thus, in total, only three different functions are used in the whole process.
In the signing process, two functions F1 and F2 are used to create two different digital signatures S1 and S2, respectively. The sender transmits the message M and the signatures S1 and S2 to the receiver. On receiving the message and the two signatures, the receiver computes two verification codes V1 and V2 with the help of the functions F1 and F3, respectively. Now, the receiver compares two codes V1 and V2; if both are congruent, the message is accepted; otherwise it is rejected. The ElGamal digital signature scheme is shown in Figure 8.3.
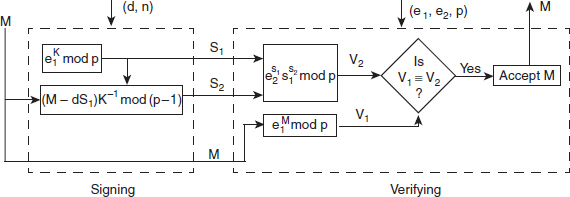
Figure 8.3 ElGamal Digital Signature Scheme
The key generation, signing and verifying algorithms for ElGamal digital signature scheme are described as follows:
Key generation: The sender generates his or her private and public keys as follows:
(i) The sender chooses a large prime number p, such that the discrete log problem is difficult in 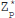 .
.
(ii) The sender then chooses his or her private key d, such that 1≤d < p−1, and computes 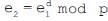 , where
, where e1 is a primitive root  . The public key of
. The public key of A is (e1, e2, p), and the private key is d.
Signing: To create the signature, the sender chooses a random number k, such that 0 < k < q, and then computes the value of S1 and S2 as follows:
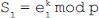
(S1 is independent of the message M)
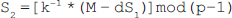
(where k−1 is the multiplicative inverse of k modulo p)
Digital signature = (S1, S2)
Verifying: The receiver verifies the signature as follows.
He or she first checks whether 0 < S1 < p and 0 < S2 < p−1, and then computes the two verification codes V1 and V2 as follows:
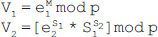
Now, the receiver tests whether V1 ≡ V2. If the condition is satisfied, the signature is accepted; else, it is rejected.
We can prove the verification as follows:

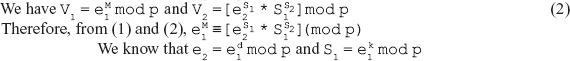
Therefore, we get:
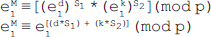
The above congruence holds if and only if:
M ≡[(d * S1) + (k * S2)]mod(p−1) or,
S2 ≡[(M−d * S1) * k−1]mod(p−1), which is same S2 as in the signing process.
10. Explain DSS, its approaches and its algorithm with proof.
Ans.: The Digital Signature Standard (DSS) was published by the National Institute of Standards and Technology (NIST) as the Federal Information Processing Standard (FIPS 186). It was originally developed in 1991. However, it was then criticized by the public because of lack of security in the scheme. Thus, it was revised in 1993, and finally in 2000, an elaborated version of DSS came into existence, which was named FIPS 186-2. The DSS uses Secure Hash Algorithm (SHA) and presents a new digital signature scheme, Digital Signature Algorithm (DSA).
As in the ElGamal digital signature scheme, in the DSS scheme also two functions F1 and F2 are used to create two different digital signatures S1 and S2, respectively. However, in DSS scheme, the message digest (not the message) is used to create the digital signature S2. The sender transmits S1, S2 and M to the receiver. On receiving the message and the two signatures, the receiver computes the message digest using the same hash function, and calculates the verification code Vc using another function F3. Now, the receiver compares Vc with S1; if both are congruent, the message is accepted; otherwise it is rejected. The DSS scheme is shown in Figure 8.4.
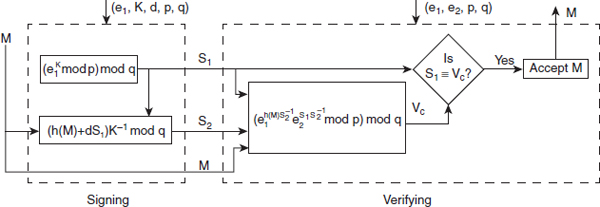
Figure 8.4 DSS Scheme
The key generation, signing and verifying algorithms for DSS scheme are described as follows. All the algorithms use the following global parameters:
L = length of the key in bits, where the number of bits are a multiple of 64; L lies between 512 and 1024 bits
p = prime number such that 2L-1 < p < 2L
q = a 160-bit prime factor of (p−1)
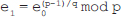 , where
, where e0 is a primitive element in Zp with 1 < e0 < p−1, such that e1 > 1
M = message to be signed
h(M) = hash of message M using the SHA algorithm
Key generation: The sender generates his or her private and public keys as follows:
 Private key: The sender chooses a random integer
Private key: The sender chooses a random integer d such that 0 < d < q; d becomes the private key of the sender
 Public key: The sender computes the following:
Public key: The sender computes the following:
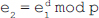
The public key of sender becomes (e1, e2, p, q)
Signing: To create the signature, the sender chooses a random number k, such that 0 < k < q, and then computes the value of S1 and S2 as follows:
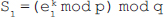
(S1 is independent of the message M)
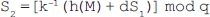
Digital signature = (S1, S2)
Verifying: The receiver verifies the signature as follows:
He or she first checks whether 0 < S1 < p and 0 < S2 < q, and then computes the digest of the message using the same hash function h(M). The receiver finally computes the verification code Vc as follows:
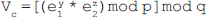
where,

(w, y and z are intermediate variables)
Now, the receiver tests whether S1 ≡ Vc. If the condition is satisfied, the signature is accepted; else, it is rejected.
Proof of the digital signature algorithm
To prove the algorithm, we have to show that Vc = S1.
As we know that:
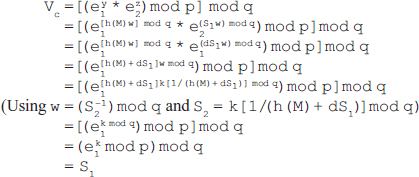
Hence, proved.
11. Why does each digital signature in the ElGamal and DSS schemes require a new value of k?
Ans.: In the ElGamal and DSS schemes, the sender chooses his or her private and public keys once and uses these keys to sign several documents. However, as we know, each time a message is sent, it should be signed with a unique digital signature; that is, no two documents can bear the same digital signature. Thus, to have a unique digital signature for every document, a new value of k (which is used in computing S1 and S2) is required.
12. How is DSS better than the RSA and ElGamal digital signature scheme?
Ans.: DSS is better than the RSA digital signature scheme because computing digital signatures in DSS requires lesser time than that in the RSA digital signature scheme for the same value of p.
DSS is also better than the ElGamal digital signature scheme because DSS scheme produces smaller digital signatures as compared to those produced by the ElGamal scheme, because q < p.
13. Explain the variations of digital signatures?
Ans.: The digital signature scheme has got many variations and additions to its main concept. Some of the variants of digital signature are discussed as follows:
 Timestamped signature: Some digital signatures include a timestamp value in order to prevent replay attacks. This is what we call timestamped signatures. In a replay attack, the documents can be replayed by a third party. For example, if
Timestamped signature: Some digital signatures include a timestamp value in order to prevent replay attacks. This is what we call timestamped signatures. In a replay attack, the documents can be replayed by a third party. For example, if A signs a request to the bank C to transfer a certain amount of money to B, B can intercept the document and replay it if there is no timestamp on the document. One way to handle such problems is to include the actual date and time. However, this may create a problem if the time zones are different or the clocks are not synchronized. Another solution is to use a nonce (which is a randomly generated number that can be used only once). The receiver makes a note that the particular nonce is used by the sender and cannot be used again. That is, a new nonce defines the present time and a used nonce defines the past time.
 Blind signature: The blind signature scheme was developed by David Chaum. The concept of blind signature is used when the sender does not want to reveal the contents of the message to the signer and just wishes get the message signed by the signer. Blind signatures are typically used in situations where the signer and the message author are completely different parties. Examples include electronic voting systems and electronic payment systems. The basic idea behind blind signatures is that the sender
Blind signature: The blind signature scheme was developed by David Chaum. The concept of blind signature is used when the sender does not want to reveal the contents of the message to the signer and just wishes get the message signed by the signer. Blind signatures are typically used in situations where the signer and the message author are completely different parties. Examples include electronic voting systems and electronic payment systems. The basic idea behind blind signatures is that the sender A first creates a message and blinds it. He then sends the blinded message to the signer B. B signs the blinded message and returns the signature on the blinded message to A. A unblinds the signature to obtain a signature on the original message.
Blind signatures scheme can be implemented by using a number of public-key digital signature schemes such as RSA and DSS. Here, we will discuss the implementation using a variation of the RSA scheme. The steps are as follows:
1. A selects a random number b, which is sometimes known as the blinding factor.
2. A calculates the blinded message as follows:
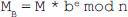
where, e = B's public key
M = original message
n = modulus defined in the RSA digital signature scheme
3. A sends MB to B.
4. B signs MB using the signing algorithm defined in the RSA digital signature scheme, as follows:
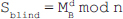
where,
Sblind = signature on the blind version of message
d = B's private key
5. A removes the blind from the signature using the multiplicative inverse of b, as follows:
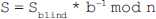
It can be easily proved that S ≡ Md (mod n); that is, the signature made on the original message M as defined in the RSA digital signature scheme. The proof is as follows:
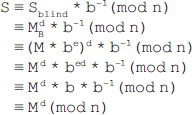
Hence, proved.
In the blind signature scheme, there are more chances of fraud. That is, it is possible that A gets a blind message signed by B that may later hurt him or her. For example, A may get a sign from B on a document that contains B's will. To deal with such type of situations, some laws have been passed that protect B in case he or she has signed a blind document that is against his or her interest.
 Undeniable digital signature: The digital signature schemes discussed so far consist of a signing algorithm and a verifying algorithm. That is, a signer can only create his or her signature using his or her private key, and anyone having the signer's public key can verify the signatures. Thus, the verification can be performed without the signer's consent or involvement. In some cases, a signer may not like it that anyone can verify his or her signatures. Thus, in order to increase the privacy of the signer, another scheme called undeniable digital signature scheme was proposed by David Chaum and Hans van Antwerpen in 1989. This scheme is a non-self-authenticating signature scheme in which no signatures can be verified without the signer's cooperation and notification.
Undeniable digital signature: The digital signature schemes discussed so far consist of a signing algorithm and a verifying algorithm. That is, a signer can only create his or her signature using his or her private key, and anyone having the signer's public key can verify the signatures. Thus, the verification can be performed without the signer's consent or involvement. In some cases, a signer may not like it that anyone can verify his or her signatures. Thus, in order to increase the privacy of the signer, another scheme called undeniable digital signature scheme was proposed by David Chaum and Hans van Antwerpen in 1989. This scheme is a non-self-authenticating signature scheme in which no signatures can be verified without the signer's cooperation and notification.
This scheme has three components, namely, signing algorithm, verification protocol and disavowal protocol.
 Signing algorithm: This allows the signer (say,
Signing algorithm: This allows the signer (say, A) to sign a message.
 Verification (or confirmation) protocol: This allows the signer to limit the users who can verify his or her signature. The verification process is interactive in nature and uses the challenge/response mechanism for verifying the signature, in which the verifier
Verification (or confirmation) protocol: This allows the signer to limit the users who can verify his or her signature. The verification process is interactive in nature and uses the challenge/response mechanism for verifying the signature, in which the verifier B sends a question (or challenge) to the signer A. A then sends a valid answer (response) to B, and B views the response to verify the signature.
 Disavowal (or denial) protocol: Since the verification process requires the involvement of the signer, it is quite possible that the signer can freely decline the request of the verifier. This protocol prevents the signer from proving that a signature invalid when it is valid, and vice versa. To prove that the signature is a fake,
Disavowal (or denial) protocol: Since the verification process requires the involvement of the signer, it is quite possible that the signer can freely decline the request of the verifier. This protocol prevents the signer from proving that a signature invalid when it is valid, and vice versa. To prove that the signature is a fake, A needs to take part in the denial protocol.
The main advantage of this scheme is that if a signature is invalid, a fraud signer cannot prove it valid because he or she will not be able to successfully complete the verification protocol. In the same way, a fraud signer cannot deny a signature that is valid, as he or she will not be able to successfully complete the disavowal protocol.
14. Explain the mutual authentication protocol.
Ans.: The mutual authentication protocol enables the communicating parties to mutually satisfy themselves about their identities and exchange session keys between them. The main issues with authenticated key exchange are confidentiality and timeliness. Confidentiality can be achieved by communicating the essential identification and session key information in an encrypted form so that the compromise of session keys can be prevented. Timeliness is another important issue that must be considered for preventing message replay attacks. The authenticated key exchange can be managed either using the symmetric-key encryption technique or the public-key encryption technique.
Symmetric-key encryption technique
In this technique, a trusted key distribution centre (KDC) is involved who is responsible for generating a session key that is to be used for a short duration between the two communicating parties for a particular session, as well as for distributing that key to both the parties. Each party shares a master key with the KDC, and the KDC uses the master key for distributing the session key to ensure secure distribution of session keys.
Several protocols were proposed for secret key distribution using a KDC; however, each of them had some weaknesses. Finally, in the early 1990s, a protocol was presented for secure key distribution including authentication. The steps of this protocol are as follows:
 To initiate the authentication exchange,
To initiate the authentication exchange, A generates a nonce NA and sends it to B along with its identifier IDA in plaintext. This nonce will be returned to A later in an encrypted message that includes the session key generated by KDC, to assure A of its timeliness.

B sends a message to KDC that includes its identifier IDB and a nonce NB to request KDC for a session key. B's message also includes a block that instructs KDC to issue credentials to A. This block is encrypted with the secret (or master) key shared between the KDC and B, and includes A's identifier (IDA), A's nonce (NA) and the suggested expiration time for the credentials (TE).
 KDC sends a message to
KDC sends a message to A that includes the following:
 Nonce received from
Nonce received from B(NB)
 A block containing
A block containing B's identifier (IDB) to assure A that the second party is B itself, A's nonce (NA) to assure A that this is a timely message and not a replay, a session key (KS) generated by KDC, and the time of expiration of the key (TE). This block is encrypted with the secret key shared between A and KDC, which is KA.
 A block containing
A block containing A's identifier (IDA), the session key (KS), and the time of expiration of the key (TE). This block is encrypted with the secret key shared between B and KDC (that is, KB). It serves as a “ticket” for A for subsequent authentications.
 A transmits the ticket to
A transmits the ticket to B. A also sends B's nonce encrypted with the session key (KS) to assure B that the message has come from A and not from a replay attack. B uses KS to decrypt the nonce.
These steps are summarized as given below:
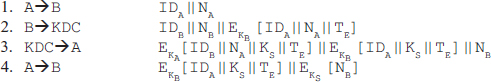
This protocol provides a secure and effective mechanism to establish a session with a secure session key. Suppose A establishes a session with B using this protocol, and then ends that session once the communication is over. Further, assume that within the same time limit TE, A again wants to establish a new session with B. Now, A has the session key KS that can be used for subsequent authentication to B but this time without the involvement of KDC. Thus, A can establish as many sessions he wants within the time limit provided by the protocol using the same session key. Once the time limit is over,
a new session key must be requested from the KDC. The steps for establishing a new session without contacting KDC are as follows:
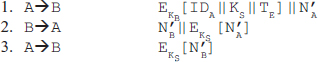
Here, N'A and N'B are newly generated nonces that assure A and B that there is no replay attack. Note that TE is the time relative to B's clock; thus, there is no need to synchronize clocks because B checks only self-generated timestamps.
Public-key encryption technique
In the public-key encryption technique, in addition to generating the session keys, KDC is also responsible for exchanging the public keys of A and B. In this technique, no master key is shared between the KDC and the communicating parties; rather, the public keys of KDC and the communicating parties are used for encryption. The steps of this protocol are as follows:
1. A sends a message to KDC informing that he or she wants to establish a secure connection with B. The message includes the identifiers of A (IDA) and B (IDB) in plaintext.
2. KDC returns a copy of the public-key certificate of B to A, which contains the identifier and public key of B (BPUB), encrypted with the private key of KDC (KDCPRI).
3. A generates a nonce NA and sends it to B along with its identifier (IDA) to inform B that he or she wants to communicate with B. A sends this information by encrypting it with B's public key (BPUB).
4. On receiving this information from A, B sends a request to KDC for issuing the public-key certificate of A, and also for generating a session key (KS). B's request includes the identifiers of A and B in plaintext, along with the nonce NA encrypted with the public key of KDC (KDCPUB).
5. KDC sends a copy of A's public-key certificate (A's identifier plus its public key) to B encrypted with KDCPRI. KDC also sends the session key (KS), nonce NA and B's identifier (IDB). This triplet informs A that KS is bound to NA in order to assure A that KS is a newly generated session key and not an old one. The triplet is first encrypted with KDCPRI to assure B that this information is from KDC itself, and then it is encrypted with B's public key to make sure that no other party can create a fraudulent connection with A.
6. B sends the triplet {NA, KS, IDB} still encrypted with KDC's private key along with the nonce NB to A. This whole information is further encrypted with A's public key (APUB).
7. A decrypts the received information using the public key of KDC (KDCPUB) to obtain the session key (KS). Then, it sends the nonce NB encrypted with the session key KS to B to assure him or her that A has got the session key.
These steps are summarized as given below:
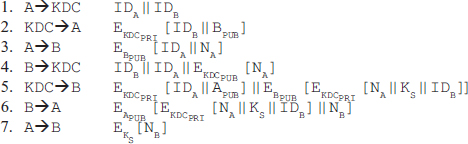
Though this protocol provides protection against several attacks, the authors Woo and Lam themselves found an error and generated a revised version of the algorithm. In the new version of the protocol, the identifier of A (IDA) is added to the information being encrypted with the private key of KDC in steps 5 and 6, as shown here:

The inclusion of IDA binds the session key KS to the identifiers of both A and B that are involved in the communication. IDA is included because of the reason that the nonce NA is considered unique among all the nonces generated by A only, and not among all nonces generated by all parties. Thus, the connection request of A is uniquely identified with the help of a pair {IDA, NA} and not only by NA as in prior protocols.
15. Explain one-way authentication protocol.
Ans.: In some applications, such as e-mail, it is not necessary for the sender and receiver to be online at the same time. The message sent by the sender is rather forwarded to the receiver's electronic mailbox, where it is stored until the receiver reads it. Thus, only one-way authentication is required.
Since the receiver may or may not be online at the time the sender sends an e-mail, a mail-handling mechanism is required that stores the e-mail when the sender sends it, and then forwards it to the receiver at some later time. As we know, an e-mail consists of a header and the message. The header of the e-mail must be clear so that it can be properly handled by the store-and-forward e-mail protocol such as SMTP.
There are two basic requirements for such applications. First, the plaintext form of the e-mail message must not be accessible to the mail-handling protocol. Thus, an e-mail message must be encrypted such that the decryption key is not known to the mail-handling system. Second, the recipient needs to be assured that the message has come from a supposed sender. One-way authentication can also be performed either using symmetric-key encryption technique or public-key encryption technique.
Symmetric-key encryption technique
While using the symmetric-key encryption technique in one-way authentication, the following steps are used.
1. The sender A sends the identifier of A and B, and a nonce N1, to the KDC in plaintext.
2. The KDC then returns a message to A, which contains a newly generated session key KS, B's identifier IDB, the nonce N1, and a block encrypted with the secret key shared between KDC and B (that is, KB). This whole message is further encrypted with the secret key shared between KDC and A (that is, KA). The inclusion of IDB and N1 in the message assures A that this is the original message and that it has not been altered by the KDC in any way. The nonce N1 also helps A in verifying that it is not a replay of some previous message. The block encrypted with KB contains KS and IDA and is intended for B. A will send this block to B as it is to establish the connection and prove A's identity.
3. A forwards to B the message originated from KDC for B, along with the e-mail encrypted with the session key KS.
The protocol is summarized as follows:
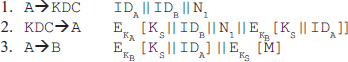
The main advantage of this protocol is that it guarantees that no user other than the intended recipient of the message will be able to read the message. Moreover, it provides a level of authentication that the message has come from an alleged sender. However, this protocol does not provide protection against replay attacks.
Public-key encryption technique
While using the public-key encryption technique for one-way authentication, one can achieve confidentiality, authentication or both. To achieve confidentiality, the sender needs to know the public key of the recipient. If A is the sender and B is the receiver, the following protocol may be used.
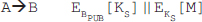
Here, A encrypts the message M with the session key KS, and also encrypts the session key KS with B's public key BPUB, and sends it to B.
To achieve only authentication, B needs to know the public key of A. Thus, the following protocol may be used.
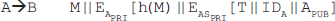
In this protocol, A sends to B the message M, the digital signature encrypted with A's private key, and A's public-key certificate encrypted with the private key of the authentication server (ASPRI). B first determines A's public key from the public-key certificate, and then verifies that it is authentic. B then uses the public key to verify the message itself.
To achieve both confidentiality and authentication, the message M can be encrypted with the session key KS, which is also sent to B encrypting it with B's public key.
16. In the RSA scheme, let p = 3, q = 11 and d = 3. Calculate the public key. Now suppose A wants to send a message M = 107 to B. Sign and verify this message using the RSA digital signature scheme.
Ans.: Here, p = 3 and q = 11
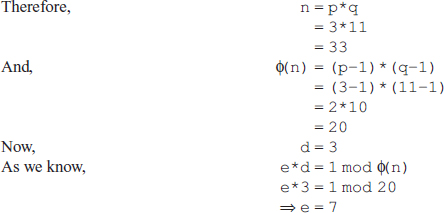
Therefore, the public key is (e, n), that is, (7, 33).
Signing:

Verifying:

Now, we have to verify whether M' ≡ M (mod n)
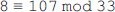
8 ≡ 8, which is true.
Thus, the signature is verified.
17. In the ElGamal scheme, let p = 881, e1 = 2 and d = 127. Calculate the value of e2. Find the values of S1, S2, V1 and V2, if M = 400 and k = 17.
Ans.: Here, p = 881, e1 = 2 and d = 127

Signing:

The multiplicative inverse of 17 in Z880 is 673 (as 17*673 = 11441 mod 880 = 1). The multiplicative inverse can be obtained using the extended Euclidean algorithm discussed in Chapter 2 (Q12).
Therefore, Equation (1) can be written as follows:
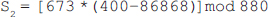
Since 86868 is not lying in Z880, we need to take 86868 mod 880, which is 628. Thus, now the equation becomes:
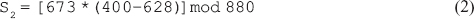
Since 400−628 comes out to be negative, we first take the additive inverse of 628, which can be computed as 880−628 = 252, and then add it to 400. Now, Equation (2) becomes

Therefore, the digital signature = (S1, S2) = (684, 556)
Verifying: Since 0 < 684 < 881 and 0 < 556 < 880, we compute the two verification codes V1 and V2 as follows:

Since V1 ≡ V2, the digital signature is verified.
18. In the DSS scheme, let q = 83, p = 997, e0 = 3 and d = 23. Calculate the values of e1 and e2. Find the values of S1, S2, V1 and V2, if h(M)= 5000 and k = 31.
Ans.: Here, q = 83, p = 997, e0 = 3 and d = 23
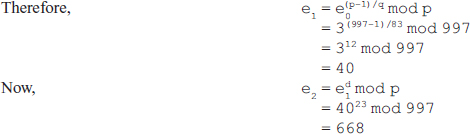
Signing:

The multiplicative inverse of 31 in Z83 is 75 (as 31*75 = 2325 mod 83 = 1).
Therefore, Equation (1) can be written as follows:

Therefore, the digital signature = (S1, S2) = (16, 50)
Verifying: Since 0 < 16 < 83 and 0 < 50 < 83, we compute the verification code Vc as follows:
We first calculate the values of intermediate variables w, z and y.
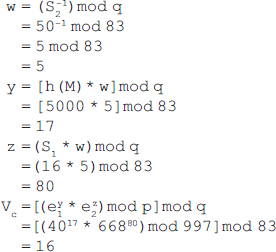
Since S1 ≡ Vc, the digital signature is verified.
Multiple-choice Questions
1. Which of the following services is not provided by digital signatures directly?
(a) Message authenticity
(b) Message confidentiality
(c) Message integrity
(d) Nonrepudiation
2. Which of the following pair of keys is used to create and verify the digital signature, respectively?
(a) Signer's private key and verifier's public key
(b) Verifier's public key and verifier's private key
(c) Signer's private key and signer's public key
(d) Signer's public key and signer's private key
3. The sender encrypts the message with his or her private key to achieve _________.
(a) Authentication
(b) Confidentiality
(c) Both (a) and (b)
(d) None of these
4. RSA _________ be used for digital signatures.
(a) can
(b) cannot
(c) must
(d) must not
5. Which of the following is a property of a digital signature?
(a) It must be able to verify the author.
(b) It must be able to verify the date and time of the signature.
(c) It must be able to authenticate the contents of the message at the time of the signature.
(d) All of these
6. Which of these is a kind of attack possible on digital signatures?
(a) Ciphertext-only attack
(b) Known-message attack
(c) Key-only attack
(d) Both (b) and (c)
7. Which of these statements is not correct about DSS?
(a) It was published by the National Institute of Standards and Technology.
(b) It uses three functions to create a digital signature.
(c) An elaborated version of DSS was named as FIPS 186-2.
(d) It uses Secure Hash Algorithm (SHA).
8. Which of these is not a variation of a digital signature?
(a) Timestamped signature
(b) Blind signature
(c) Encrypted digital signature
(d) Undeniable digital signature
Answers
1. (b)
2. (c)
3. (a)
4. (a)
5. (d)
6. (d)
7. (b)
8. (c)
1. Explain the working principle of the Kerberos protocol.
Ans.: Kerberos is an authentication protocol that has been designed to be used in an open distributed environment, where the users at workstations request for the services on the servers distributed throughout the network. It basically provides a centralized authentication server that is responsible for authenticating users to servers and servers to users. Its name has been derived from Greek mythology after the name of a three-headed dog that guarded the gates of Hades. Kerberos has become very popular as it can also act as a KDC in addition to being an authentication protocol. It was originally developed as a part of Project Athena at the MIT. Several versions of Kerberos have evolved. However, the most commonly used version of Kerberos is version 4. The Kerberos protocol has four components, namely, client workstation, authentication server (AS), ticket-granting server (TGS) and real server.
 Client workstation is an entity that wants to access services from a server.
Client workstation is an entity that wants to access services from a server.
 Authentication server (AS) acts as a KDC in the Kerberos protocol. It is responsible for the verification of the identity of users during login. To get verified, the users first need to register themselves with the AS. Each registered user is assigned a unique ID and a password. All the IDs and their corresponding passwords are stored in a centralized database of AS. In addition to verifying the users, it also issues a session key to the requesting user, which is to be used between the user and the TGS, and sends a ticket for the TGS. AS also shares a unique secret key with each server, and hence, all the servers also need to register themselves with AS.
Authentication server (AS) acts as a KDC in the Kerberos protocol. It is responsible for the verification of the identity of users during login. To get verified, the users first need to register themselves with the AS. Each registered user is assigned a unique ID and a password. All the IDs and their corresponding passwords are stored in a centralized database of AS. In addition to verifying the users, it also issues a session key to the requesting user, which is to be used between the user and the TGS, and sends a ticket for the TGS. AS also shares a unique secret key with each server, and hence, all the servers also need to register themselves with AS.
 Ticket-granting server (TGS) is responsible for issuing tickets for establishing connection with the real server. It also issues the session key, which is to be used between the user and the real server. Once a user has got verified by AS, he or she can contact TGS any number of times to obtain the tickets for different real servers.
Ticket-granting server (TGS) is responsible for issuing tickets for establishing connection with the real server. It also issues the session key, which is to be used between the user and the real server. Once a user has got verified by AS, he or she can contact TGS any number of times to obtain the tickets for different real servers.
 Real server provides the required services to the user. Here, the user uses its own process (client process) to access the server process using a client-server program (e.g. FTP).
Real server provides the required services to the user. Here, the user uses its own process (client process) to access the server process using a client-server program (e.g. FTP).
The working of Kerberos is shown in Figure 9.1. To understand how the Kerberos protocol operates, consider a user A who wants to access the services of a real server B. The user A can access the processes running on B by performing the following steps.
1. The user A logs in to the workstation by entering his or her user ID (say, IDA). The workstation then sends IDA in plaintext to AS.
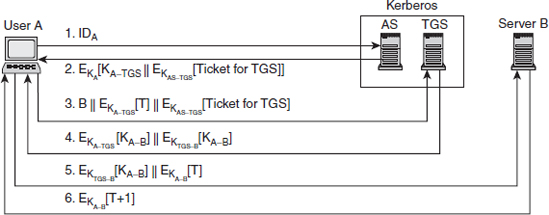
Figure 9.1 Kerberos Protocol
2. In response, the AS creates a message that includes two items: a randomly generated session key KA−TGS and the ticket for TGS, which is encrypted with the secret key shared between the AS and TGS (KAS−TGS). This whole message is encrypted with the symmetric key of A (KA). The session key KA−TGS is used by the user to contact the TGS. Now, this encrypted message is sent to A.
3. On receiving the message, A's workstation asks him or her for the password. When A enters the correct password, the workstation generates the symmetric key (KA) by applying an appropriate algorithm (generally a hash function) on the password. The password is then immediately destroyed, so that it cannot be stolen by anyone. The symmetric key KA is now used to decrypt the received message. Once the message is decrypted, the ticket for TGS and the session key KA−TGS are extracted. Since the ticket is encrypted with the symmetric key of TGS, only TGS can open it. A now sends a message to TGS containing the ticket received from AS, the name of the real server (B) and a timestamp T encrypted with the session key KA−TGS. This timestamp prevents replay attacks from any other user.
4. The TGS now sends two tickets each for A and B. Both these tickets contain the session key (KA−B) to be used between A and B. A's ticket is encrypted with the secret key (KA−TGS) shared between A and TGS, while the ticket for B is encrypted with the secret key (KTGS−B) shared between TGS and B. This mechanism provides security for the whole process. No other user can extract KA−B, as he or she does not know KA−TGS or KTGS−B. Moreover, step 3 cannot be replayed, since an unauthorized user cannot replace the timestamp with a new one (as he or she does not know KA−TGS).
5. A now sends B's ticket with a timestamp encrypted with KA−B.
6. B acknowledges the receipt of the ticket by adding 1 to the timestamp. It also encrypts the message with KAB and sends it to A.
Now, suppose A wishes to receive services from different servers, then it only has to repeat steps 3 to 6. The first two steps involve the verification of A's identity, which remains same for all the servers. Thus, steps 1 and 2 need not be repeated.
2. Discuss the basic requirements for Kerberos.
Ans.: There are four basic requirements that have been defined for Kerberos. These requirements are as follows:
 Security: Kerberos should be secure enough to prevent eavesdroppers from obtaining any kind of information that is necessary to impersonate a user.
Security: Kerberos should be secure enough to prevent eavesdroppers from obtaining any kind of information that is necessary to impersonate a user.
 Reliability: Kerberos should be highly reliable and should support distributed server architecture so that, in case of failure of one system, some other system can act as a backup.
Reliability: Kerberos should be highly reliable and should support distributed server architecture so that, in case of failure of one system, some other system can act as a backup.
 Transparency: Kerberos should be transparent, such that the user is not able to know that authentication is taking place; the user should only be required to enter his or her password.
Transparency: Kerberos should be transparent, such that the user is not able to know that authentication is taking place; the user should only be required to enter his or her password.
 Scalability: Kerberos should support a modular, distributed architecture, so that it can support a large number of clients and servers.
Scalability: Kerberos should support a modular, distributed architecture, so that it can support a large number of clients and servers.
3. Define the terms ‘Kerberos realm’ and ‘Kerberos principal’.
Ans.: A typical Kerberos environment consists of an authentication server (or a Kerberos server), a number of clients all registered with the authentication server and a number of application servers that provide several services. The Kerberos server must maintain a centralized database that contains the user IDs and hashed passwords of all the users registered with the Kerberos server. It must also share a unique secret key with each application server. All servers need to get registered with the Kerberos server. Such an environment is called Kerberos realm. It is basically a single administrative domain.
The computer system where the Kerberos database is stored (referred to as Kerberos master computer system) should be kept in a physically secure room. The person having the Kerberos master password is only authorized to modify the contents of the Kerberos database. Though several read-only copies of this database can be kept on other Kerberos computer systems, changes can only be made on the master computer system. If there exist several Kerberos realms, then they must share secret keys and trust among themselves.
Kerberos principal is a unique identity to which Kerberos can assign tickets. In other words, all the services or the users known to a Kerberos system are referred to as Kerberos principals. Each Kerberos principal is identified by its principal name. A Kerberos principal has the following form:
primary[/instance]@REALM
Principal is divided into three parts: the primary (service or user name), the instance, and the realm.
 Primary: This is the first part of the principal. For a user, the primary is the
Primary: This is the first part of the principal. For a user, the primary is the username and, for a host, the primary is the word host.
 Instance: This is an optional string that qualifies the primary, and is separated from the primary by a slash (/). In case of a user, the instance is generally
Instance: This is an optional string that qualifies the primary, and is separated from the primary by a slash (/). In case of a user, the instance is generally NULL; however, in some cases, it can have some value (e.g. admin).
 Realm: This is the last component of the principal, and is basically the Kerberos realm. It is generally separated from the rest of the principal by the ‘@’ symbol. In most cases, it is your domain name and must be specified in upper-case letters.
Realm: This is the last component of the principal, and is basically the Kerberos realm. It is generally separated from the rest of the principal by the ‘@’ symbol. In most cases, it is your domain name and must be specified in upper-case letters.
For example, consider the following principals:
robert@ATHENA.MIT.EDU robert/admin@ATHENA.MIT.EDU
In the first principal, robert is primary, instance is NULL and ATHENA.MIT.EDU is realm. In the second principal, robert is primary, admin is instance and ATHENA.MIT.EDU is realm.
4. Discuss the steps involved in inter-realm communication in Kerberos.
Ans.: In a system that crosses organizational boundaries, it is not feasible for all users to be registered with a single AS; rather, multiple ASs will exist with each AS responsible for the registration and authentication of the users and servers within a single realm. In case two users (say, A and B) of
different realms want to communicate with each other, they need to obtain service tickets to access resources in foreign realms. In order to access such services, these steps are followed:
1. The user A contacts the AS of their realm asking for a ticket that will be used with the TGS of the foreign realm. If both the realms share keys and have established a trusted relationship between them, the corresponding AS of A's realm delivers the requested ticket to A.
2. In case A's realm does not share keys with the foreign realm, the AS of A's realm will provide a ticket for an intermediary foreign realm that may be sharing the keys with the target realm.
3. The client can use this ‘intermediary ticket’ to communicate with the AS of the intermediary foreign realm, which will either follow step 2, or it will issue a ticket that can be used with the AS of the target realm (in case it shares keys with the target realm).
4. The client uses this ticket to obtain the service ticket from the TGS of the foreign realm.
5. The user can now use this service ticket to obtain the services of the desired server.
5. How is the encryption key generated from the password in Kerberos?
Ans.: In Kerberos, the user can enter a password of any length; however, the password is restricted to contain only those characters that can be represented in a 7-bit ASCII format. This password is used to generate the symmetric key of the user that is to be used for decrypting the messages received from AS. The steps involved in password-to-key transformation are as follows:
1. The user enters his or her password in the form of a character string (say, s).
2. The character string s is converted into a bit string (say, b) in such a way that the first character of s is stored in the first seven bits of b, the second character is stored in next seven bits and so on, as shown in Figure 9.2(a). That is:
b[0]represents bit 0 ofs[0]…b[6]represents bit 6 ofs[0]b[7]represents bit 0 ofs[1]…b[13]represents bit 6 ofs[1]…b[7i+j]represents bitjofs[i]where, 0 <=j<= 6
3. The bits in the bit string b are aligned in a ‘fanfold’ manner, such that the bits 0 to 55 form the first row, then the bit 56 is placed below the bit 55, bit 57 is placed below 54, bit 58 is placed below 53 and so on, as shown in Figure 9.2(b).
4. A bitwise XOR operation is performed to compact the bit string to 56 bits. For example, if the bit string is of length 60, then
b[55] = b[55]  b[56]
b[56]
b[54] = b[54]  b[57]
b[57]
b[53] = b[53]  b[58]
b[58]
b[52] = b[52]  b[59]
b[59]
This creates a 56-bit DES key [see Figure 9.2(b)]. Note that steps 3 and 4 are performed to compact the bit string.
5. The 56-bit string is then expanded to a 64-bit input key K. For this, the 56-bit key is divided into 7-bit blocks (total 8 blocks), and then each 7-bit block is mapped to a corresponding block of 8 bits, thus creating a 64-bit key.
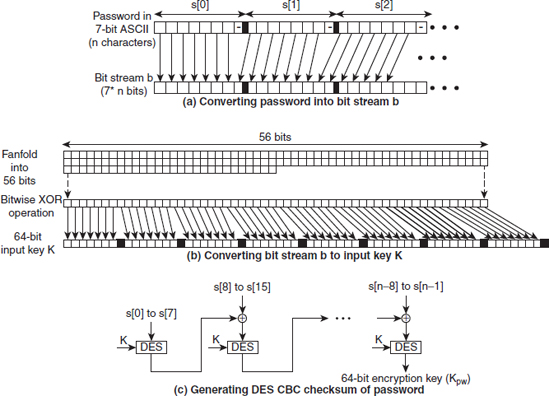
Figure 9.2 Password-to-key transformation in Kerberos
6. The password supplied by the user is encrypted with the key K using the cipher block chaining (CBC) mode of DES [see Figure 9.2(c)]. This process results in a 64-bit block, referred to as CBC checksum, which becomes the encryption key (say, Kpw) associated with the user's password.
6. Explain the differences between Kerberos version 4 and Kerberos version 5.
Ans.: Though Kerberos version 4 is most commonly used, it suffers from some environmental shortcomings and technical deficiencies. Kerberos version 5 attempts to overcome these problems. The differences between Kerberos versions 4 and 5 based on the environmental shortcomings are listed in Table 9.1.
| Issue | Kerberos 4 | Kerberos 5 |
|---|---|---|
| Encryption system dependence | Requires the use of DES algorithm. | Any encryption algorithm can be used. To make this possible, an encryption type identifier is attached with the ciphertext. |
| Internet protocol dependence | Uses only IP addresses, and no other address can be used in it. | Allows the use of any network address, such as the ISO network address. This is possible due to the reason that the network addresses are labelled with type and length. |
| Message byte ordering | The byte ordering in the message is not uniform. The sender can include either the least significant byte or the most significant byte in the lowest address. That is, the sender has the freedom of choosing his or her own byte ordering. | The byte ordering in the message is uniform. All the message structures are defined using two standards, namely, Abstract Syntax Notation One (ASN.1) and Basic Encoding Rules (BER), thereby providing unambiguous byte ordering. |
| Ticket lifetime | The lifetime of the ticket is limited. The lifetime values are encoded in 8-bit quantities, in units of 5 minutes. Thus, the maximum possible lifetime is 28 * 5 = 1280 minutes or 21 hours, approximately. This time limit may not be sufficient for some applications, such as a long-running simulation. | The tickets can have arbitrary lifetime values. To allow this, an explicit start and end time is included with each ticket. |
| Authentication forwarding | The credentials issued to one client cannot be forwarded to some other host or some other client. | The credentials issued to one client can be forwarded to another. This would allow a client to access a server, and that server to access another server on behalf of the client's credentials. This technique is termed as transitive cross-realm authentication. For example, a print server can access the file server to retrieve the file to be printed on behalf of the client. |
| Inter-realm authentication | The number of Kerberos-to-Kerberos relationships required for interoperability among N realms is calculated as N2 , where N is the number of realms. |
A lesser number of relationships are required. |
In addition to the environmental shortcomings mentioned in the preceding text, version 4 suffers from some technical deficiencies. Version 5 is intended to address these deficiencies. These deficiencies are listed in Table 9.2.
| Issue | Kerberos 4 | Kerberos 5 |
|---|---|---|
| PCBC encryption | Uses a nonstandard mode of the DES algorithm known as propagating cipher block chaining (PCBC) for encryption. The PCBC was supposed to provide an integrity check as part of the encryption operation; however it is found to be prone to an attack that involves the interchange of ciphertext blocks. | Uses the standard cipher block chaining (CBC) mode for encryption. It provides explicit integrity mechanisms such as attaching hash code or checksum to the message before encryption using CBC. |
| Session keys | The session key included in each ticket serves two purposes. First, it is used by the client to encrypt the authenticator sent to the server associated with that ticket. Second, it can be used to encrypt the messages between a client and a server. Since the same ticket is used more than once for accessing a particular server, it leads to the possibility of a replay attack by a third party. | Allows a client and a server to negotiate a sub-session key, which is to be used only for the current session. Thus, if the client wishes to access the server again, he or she would require a new sub-session key. |
| Password attacks | Does not provide a secured mechanism for preventing password attacks. Whenever AS sends a message to the client, it is encrypted with the key based on the client's password. This message can be captured by an opponent who may then attempt to decrypt it by trying various passwords. If the opponent chooses the right mechanism to acquire the password, then he or she can use it to acquire the authentication credentials from Kerberos. | Though version 5 does not completely prevent the password attacks, it provides a preauthentication mechanism that makes the password attacks more difficult. |
7. Define the terms forwardable, renewable and postdatable tickets.
Ans.: Kerberos version 5 supports the use of forwardable, renewable and postdatable tickets.
 Forwardable ticket: This ticket can be used by the user to get a new ticket on behalf of the current credentials. This allows the user to get validated on other machines also. However, the user has to use a different IP address.
Forwardable ticket: This ticket can be used by the user to get a new ticket on behalf of the current credentials. This allows the user to get validated on other machines also. However, the user has to use a different IP address.
 Renewable ticket: As the name suggests, this ticket can be renewed by asking the KDC to issue a new ticket with an extended lifetime. Note that a ticket can only be renewed before the expiration of its time limit. It is similar to renewing an insurance policy or a credit card before the validity is expired.
Renewable ticket: As the name suggests, this ticket can be renewed by asking the KDC to issue a new ticket with an extended lifetime. Note that a ticket can only be renewed before the expiration of its time limit. It is similar to renewing an insurance policy or a credit card before the validity is expired.
 Postdatable ticket: This ticket is similar to a postdated cheque, which bears a starting time as some time in the future. Thus, the ticket is initially invalid. A postdatable ticket can only be used after getting it validated from the KDC during its valid lifetime.
Postdatable ticket: This ticket is similar to a postdated cheque, which bears a starting time as some time in the future. Thus, the ticket is initially invalid. A postdatable ticket can only be used after getting it validated from the KDC during its valid lifetime.
8. Explain the X.509 authentication service and its certificates.
Ans.: X.509 was designed by ITU-T to describe the public-key certificates in a structured way. It is a part of the X.500 series of recommendations that define a directory service. A directory is basically a server or a set of servers distributed over a network that maintains a database of information about the users, such as mappings from user names to network addresses. X.509 provides authentication services to its users through the X.500 directory, which may act as the repository of public-key certificates associated with each user. Each certificate contains the public key of the user and is signed by the private key of the trusted certification authority (CA). It may be noted that only the CA can create the user certificates and place them in the directory. The directory server itself is not responsible for creating public keys or certificates; it simply acts as a warehouse of certificates for the users.
X.509 also defines a set of alternative authentication protocols based on the use of public-key certificates. The format of the certificate and the authentication protocols defined in X.509 are used in several contexts such as IP Security, S/MIME, SSL/TLS and SET, and hence it is considered to be an important standard.
The first version of X.509 was issued in 1988. Then, in 1993, its second version came out, to address some of the security concerns. A third version was released in 1995, which was revised in 2000. X.509 makes uses of the ASN.1 (Abstract Syntax Notation One) protocol, which defines the general format of the X.509 certificate with several fields, as shown in Figure 9.3. The description of these fields is as follows:
 Version number: This field differentiates among the various versions of the certificate format. That is, the version of X.509 is specified in this field. The first version number was 0, and the current version (third version) is 2.
Version number: This field differentiates among the various versions of the certificate format. That is, the version of X.509 is specified in this field. The first version number was 0, and the current version (third version) is 2.
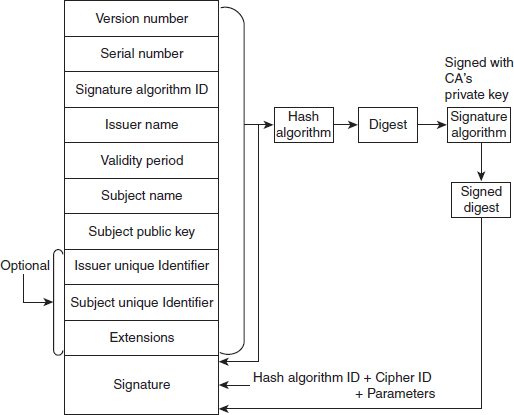
Figure 9.3 X.509 Certificate Format
 Serial number: This field contains an integer value assigned to each certificate. This value is unique within the issuing CA.
Serial number: This field contains an integer value assigned to each certificate. This value is unique within the issuing CA.
 Signature algorithm ID: This field specifies the algorithm used by CA to sign the certificate, together with any associated parameters.
Signature algorithm ID: This field specifies the algorithm used by CA to sign the certificate, together with any associated parameters.
 Issuer name: This field specifies the name of the CA that has created and signed the certificate. The name is usually specified as a hierarchy of strings that include the name of the country, state, organization, department and so on.
Issuer name: This field specifies the name of the CA that has created and signed the certificate. The name is usually specified as a hierarchy of strings that include the name of the country, state, organization, department and so on.
 Validity period: This field specifies the lifetime of the certificate. It includes the earliest time and latest time; the certificate is invalid before the earliest time and after the latest time.
Validity period: This field specifies the lifetime of the certificate. It includes the earliest time and latest time; the certificate is invalid before the earliest time and after the latest time.
 Subject name: This field specifies the entity to which this certificate refers. That is, this certificate certifies the public key of the user who is holding the corresponding private key. This field is also specified as a hierarchy of strings; one of the strings is called the common name, which is the actual name of the user.
Subject name: This field specifies the entity to which this certificate refers. That is, this certificate certifies the public key of the user who is holding the corresponding private key. This field is also specified as a hierarchy of strings; one of the strings is called the common name, which is the actual name of the user.
 Subject public key: This field specifies the main content of the certificate, which is the public key. It also specifies the corresponding public-key algorithm and its associated parameters.
Subject public key: This field specifies the main content of the certificate, which is the public key. It also specifies the corresponding public-key algorithm and its associated parameters.
 Issuer unique identifier: This is an optional field that specifies the unique identifier of the authority issuing the certificate. This field allows having the same value in the issuer name field of two different certificates, provided they have different values in the issuer unique identifier field.
Issuer unique identifier: This is an optional field that specifies the unique identifier of the authority issuing the certificate. This field allows having the same value in the issuer name field of two different certificates, provided they have different values in the issuer unique identifier field.
 Subject unique identifier: This is also an optional field, which specifies the unique identifier of the subject to which the certificate is issued. This field allows having the same value in the subject name field of two different certificates, provided they have different values in the subject unique identifier field.
Subject unique identifier: This is also an optional field, which specifies the unique identifier of the subject to which the certificate is issued. This field allows having the same value in the subject name field of two different certificates, provided they have different values in the subject unique identifier field.
 Extensions: This field is used by the issuers to add more private information to the certificate. The extensions were added in the third version of X.509. This is also an optional field.
Extensions: This field is used by the issuers to add more private information to the certificate. The extensions were added in the third version of X.509. This is also an optional field.
 Signature: This field is divided into three sections as discussed in the following:
Signature: This field is divided into three sections as discussed in the following:
 The first section includes all the other fields in the certificate.
The first section includes all the other fields in the certificate.
 The second section contains the digest of the first section, which is encrypted with the private key of CA.
The second section contains the digest of the first section, which is encrypted with the private key of CA.
 The third section includes the algorithm identifier that has been used to create the second section.
The third section includes the algorithm identifier that has been used to create the second section.
9. Explain the terms certificate renewable and certificate revocation with respect to X.509. Also, discuss how the format of the X.509 certificate is different from that of the certificate revocation list?
Ans.: The X.509 certificates have a validity associated with them. If everything goes smoothly, then the certificates can be renewed by the CA. A new certificate is issued before the validity of the old one expires. This process is known as certificate renewal. However, sometimes, the certificate has to be revoked before the validity of the certificate expires. This is known as certificate revocation. The certificates can be revoked due to several reasons. Some of them are as follows:
 The private key of the user might have been compromised.
The private key of the user might have been compromised.
 The private key of the CA that can verify the certificates might have been compromised. In this case, the CA must revoke all unexpired certificates.
The private key of the CA that can verify the certificates might have been compromised. In this case, the CA must revoke all unexpired certificates.
 The certificate authority is no longer willing to issue a certificate to the user.
The certificate authority is no longer willing to issue a certificate to the user.
The certificate revocation is implemented by periodically issuing a Certificate Revocation List (CRL), which contains all the revoked certificates that have not expired till the issue date of the CRL. A typical format of CRL is shown in Figure 9.4. It contains many fields, some of which are the same as in the X.509 certificate. The fields common to both X.509 certificates and CRL are signature algorithm ID, issuer name and signature. The fields that are new in CRL are as follows:
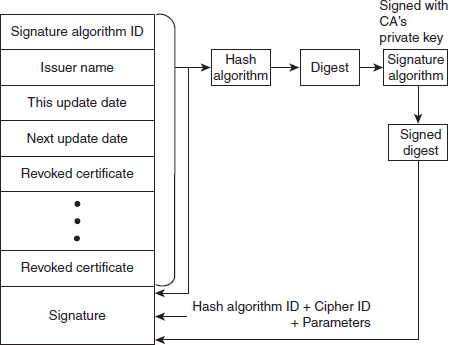
Figure 9.4 Certificate Revocation List Format
 This update date: This field defines the issue date of CRL.
This update date: This field defines the issue date of CRL.
 Next update date: This field specifies the date when the list will be issued next.
Next update date: This field specifies the date when the list will be issued next.
 Revoked certificate: This is a repeated list of all the certificates that are not expired and have been revoked. Each list is divided into two sections, namely, user certificate serial number and revocation date.
Revoked certificate: This is a repeated list of all the certificates that are not expired and have been revoked. Each list is divided into two sections, namely, user certificate serial number and revocation date.
10. What do you understand by directory authentication service?
Ans.: The directory authentication service is used when two entities wish to communicate with each other, and each of them needs to authenticate the other. That is, both the sender and receiver need to ensure that the other communicating party is the one that it claims to be. There are two types of directory authentication services, namely, peer entity authentication and data origin authentication.
 Peer entity authentication: This authentication service enables the user to verify the identity of a peer entity involved in the communication process. It prevents an entity from masquerading as another entity or an unauthorized replay of a previously established connection. The peer entity service can be used during the establishment phase or occasionally during the data transfer phase of a connection. Note that there must be an association between the two parties for peer entity authentication.
Peer entity authentication: This authentication service enables the user to verify the identity of a peer entity involved in the communication process. It prevents an entity from masquerading as another entity or an unauthorized replay of a previously established connection. The peer entity service can be used during the establishment phase or occasionally during the data transfer phase of a connection. Note that there must be an association between the two parties for peer entity authentication.
 Data origin authentication: This authentication service enables the recipient to verify that the message has not been tampered with in transit (data integrity) and that it has originated from the expected sender (authenticity). That is, it is used to verify the original source of a received message. The data origin authentication services allow the receiver to verify the identity of the message as belonging to the original message creator even if the message has passed through one or more intermediaries before arriving at the receiver. Note that unlike peer entity authentication, no association between the sender and receiver is required. Thus, this type of service is suitable for e-mail service in which there is initially no communication between the entities.
Data origin authentication: This authentication service enables the recipient to verify that the message has not been tampered with in transit (data integrity) and that it has originated from the expected sender (authenticity). That is, it is used to verify the original source of a received message. The data origin authentication services allow the receiver to verify the identity of the message as belonging to the original message creator even if the message has passed through one or more intermediaries before arriving at the receiver. Note that unlike peer entity authentication, no association between the sender and receiver is required. Thus, this type of service is suitable for e-mail service in which there is initially no communication between the entities.
11. Discuss the authentication procedures of X.509.
Ans.: X.509 includes three authentication procedures, namely, one-way authentication, two-way authentication and three-way authentication. These authentication procedures make use of public-key signatures and can be used across a variety of applications. While working with these procedures, it is assumed that two communicating nodes know each other's public key. These procedures are discussed in the following.
 One-way authentication: This involves a single transfer of information from user
One-way authentication: This involves a single transfer of information from user A to user B [see Figure 9.5(a)]. This information is transferred in order to confirm that the message is generated by user A, and that the message is intended for user B and has not been altered or replayed by any intruder. Thus, this procedure only verifies the identity of A. At a minimum, the message includes the following and is signed with the private key of A.
 Timestamp (
Timestamp (tA): This indicates the time when the message was generated, along with the validity or expiration time of the message.
 Nonce (
Nonce (rA): This is a random number used to protect the message from replay attacks. The value of nonce must be unique during the validation period. This is done so that B can discard any new messages having the same nonce value.
 Identity of
Identity of B (IDB): This is included so that the user B can access the X.509 directory and be sure that the message is intended for him or her only.
 Signed data (
Signed data (sgnData): This is the information that is actually conveyed between the two users. This information is included within the scope of the signature, thus ensuring its authenticity and integrity.
 Encrypted data (
Encrypted data (EBPUB[KAB]): This includes the session key KAB, encrypted with B's public key (BPUB). This key is used after the authentication process gets over.
 Two-way authentication: This involves a two-way transfer of information; first from user
Two-way authentication: This involves a two-way transfer of information; first from user A to B, and then from user B to A. This two-way transfer allows both users to verify each other's identity. First, A sends a message containing the same fields as described in one-way authentication to B. Then, B replies to A with a message including tB, rB, IDA, rA, sgnData and optionally EAPUB[KAB], and the message is signed by B [see Figure 9.5(b)]. The inclusion of nonce rA in the reply message ensures that the reply is valid and has come from B, whereas rB protects the information being transferred by B from replay attacks.
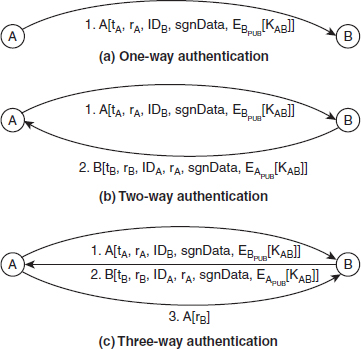
Figure 9.5 Authentication Procedures
 Three-way authentication: This involves the three-way transfer of information from
Three-way authentication: This involves the three-way transfer of information from A to B. In this procedure, a third message from A to B is included, in addition to two messages that are the same as described in two-way authentication. The third message contains a signed copy of the nonce rB signed by A [see Figure 9.5(c)]. Since both the nonces are echoed back by the other side, each user can check the returned nonce to detect replay attacks. This approach is useful when synchronized clocks are not available.
12. Explain the services of PGP.
Ans.: PGP (stands for pretty good privacy) is a simple protocol that was invented by Phil Zimmermann to provide confidentiality, authentication and integrity services for electronic mail and other file storage applications. PGP offers various services, which are discussed as follows:
Authentication only
PGP provides digital signature service for authentication. Suppose user A wants to send a message to B, then, to achieve authentication, these steps are followed.
1. A creates a message, and applies the SHA-1 algorithm to find the 160-bit hash code of the message.
2. The generated hash code is encrypted with RSA using A's private key. The resultant encrypted code is then added to the beginning of the message.
3. On receiving the message, B decrypts the message with RSA using A's public key and extracts the hash code.
4. A new hash code for the message is also generated at B's end, and it is compared with the decrypted hash code. If both are same, the message is accepted as authentic; otherwise it is rejected.
Due to the use of both SHA-1 and RSA, the digital signature scheme becomes effective. The use of RSA assures the receiver that the signature can only be generated by the owner of the private key, whereas SHA-1 ensures that no intruder can create a new message with the same hash code, and hence, the signature of the original message. Alternatively, signatures can also be generated using DSS/SHA-1.
Confidentiality only
The confidentiality service is provided by encrypting the messages that are to be transmitted, or to be stored on the local server. The three commonly used symmetric encryption algorithms are CAST-128, IDEA and 3DES. Note that, in PGP, each session key is used only once, and hence, a new key needs to be generated each time a message is to be transmitted. The key is generated as a random 128-bit number, bound to the message and transmitted with it. To provide protection for the key, it is encrypted with the receiver's public key. The steps to achieve confidentiality are as follows.
1. A creates a message and a random 128-bit number. This number is used as a session key K for this message.
2. A encrypts the message using the CAST-128 (or IDEA or 3DES) encryption algorithm with the session key K.
3. The session key K is encrypted with B's public key using RSA (or ElGamal). The encrypted key is then added to the beginning of the message.
4. On receiving the message, B uses its private key to decrypt and recover the session key K.
5. The message is finally decrypted using the session key K.
Confidentiality and Authentication
In some cases, both the confidentiality and authentication services are required for the same message. In such situations, the following sequence is used:
1. The sender A first signs the plaintext message using his or her private key. The signature is then added to the beginning of the message.
2. The signature and the plaintext message together are encrypted with the session key using CAST-128, IDEA or the 3DES algorithm.
3. The session key is encrypted with B's public key using the RSA or ElGamal algorithm.
4. On receiving the message, B uses its private key to decrypt and recover the session key K.
5. B then decrypts with session key K to recover the plaintext message and signature.
6. To verify the signature, a new hash code for the message is computed at B's end and compared with the decrypted hash code. If both are the same, the message is accepted as authentic; otherwise, it is rejected.
Compression
By default, PGP compresses the messages using the ZIP compression algorithm after applying the signature, however, before encrypting them. This saves space for e-mail transmission as well as for file storage. There are two reasons for signing an uncompressed message, which are discussed in the following:
 Generally, the signed messages along with signatures need to be stored for future verification. If an uncompressed message is signed, then the message and the signature can be stored together and retrieved when verification is required. However, if a compressed message is signed, then either the compressed message needs to be stored or the message needs to be recompressed when verification is required.
Generally, the signed messages along with signatures need to be stored for future verification. If an uncompressed message is signed, then the message and the signature can be stored together and retrieved when verification is required. However, if a compressed message is signed, then either the compressed message needs to be stored or the message needs to be recompressed when verification is required.
 Even if the user is ready to recompress the message dynamically for verification, then also PGP's compression algorithm presents certain problems. The main problem is that the algorithm is nondeterministic in nature; that is, the various implementations of the algorithm produce different compressed forms at different times. This is because they achieve different tradeoffs in running speed versus compression ratio. However, all the implementations are interoperable as any version of the algorithm can correctly decompress the output of any other version. If the signature is created after compression, it would restrict all PGP implementations to use the same version of the compression algorithm.
Even if the user is ready to recompress the message dynamically for verification, then also PGP's compression algorithm presents certain problems. The main problem is that the algorithm is nondeterministic in nature; that is, the various implementations of the algorithm produce different compressed forms at different times. This is because they achieve different tradeoffs in running speed versus compression ratio. However, all the implementations are interoperable as any version of the algorithm can correctly decompress the output of any other version. If the signature is created after compression, it would restrict all PGP implementations to use the same version of the compression algorithm.
Encrypting the message after encryption strengthens the cryptographic security. Since, the compressed message contains less redundancy than the plaintext (or uncompressed) message, it would be more difficult to perform cryptanalysis.
E-mail Compatibility
When PGP is used, the encryption has to be done in at least a portion of the message to be transmitted. These encrypted blocks are made of a stream of arbitrary 8-bit octets that are not supported by many e-mail systems as they permit the use of only ASCII text. To make the encrypted blocks compatible with e-mail systems, PGP converts the 8-bit octets into a stream of printable ASCII characters. For this, it uses the radix-64 conversion scheme. In this scheme, each group of three octets is converted into four ASCII characters. A CRC is also added at the end of the block for detecting any transmission errors.
One problem with this conversion scheme is that it expands a message by 33%. Thus, the message needs to be more compressed so that it compensates for the radix-64 expansion. Another main disadvantage of the radix-64 format is that it blindly performs the conversion regardless of the content, even if the input is ASCII text. Thus, when a message containing ASCII text is signed but not encrypted will be converted by radix-64, the output becomes unreadable for the normal user. To overcome this, PGP can be configured to convert only the signature part to radix-64 format, thus making the message readable by normal users without using PGP. The signature would still have to be verified using PGP.
Segmentation and Reassembly
E-mail facilities generally impose a restriction on the maximum length of the message to be transmitted (generally 50,000 octets). Thus, to send a message having length longer than maximum specified, it has to be broken down into smaller parts, and each part needs to be mailed individually. To achieve this, PGP uses segmentation and reassembly functions. If a PGP message is too large, then it is broken down into smaller segments that are of standard e-mail message size. The segmentation is performed after all other processing on the message has been done (even after radix-64 conversion); otherwise, all the processing needs to be done on each segment. Thus, only the first segment contains the session key component and signature component of the message. The segmented message is reassembled at the receiver's end, removing the e-mail headers from each segment. It must be noted that reassembling is performed before applying radix-64 conversion, decryption and decompression.
13. Discuss the steps that are followed for the transmission and reception of PGP messages.
Ans.: The PGP messages are transmitted from the sender to receiver using the following steps:
1. If signature is required, the hash code of the uncompressed plaintext message is created and encrypted using the sender's private key.
2. The plaintext message plus the signature are compressed using the ZIP compression algorithm.
3. The compressed plaintext message plus compressed signature (if present) are encrypted with a randomly generated session key to provide confidentiality. The session key is then encrypted with the recipient's public key and is added to the beginning of the message.
4. The entire block is converted to radix-64 format.
On receiving the PGP message, the receiver follows the reverse process, as described in the following:
1. The entire block is first converted back to binary format.
2. The recipient recovers the session key using his or her private key, and then decrypts the message with the session key.
3. The decrypted message is then decompressed.
4. If the message is signed, the receiver needs to verify the signature. For this, he or she computes a new hash code and compares it with the received hash code. If they match, the message is accepted; otherwise, it is rejected.
14. What are key rings in PGP?
Ans.: When a sender needs to send messages to many people, then he or she requires the key rings. In this case, a sender needs to have two sets of rings—one is a ring of private/public keys, and other is a ring of public keys. The ring of private/public keys includes different key pairs of public and private keys that are owned by the sender, and the ring of public keys includes public key of each user with whom the sender wants to communicate. There are two reasons for keeping various pairs of private/public keys, which are discussed as follows:
 The sender might wish to change his private/public key pair from time to time for more secured communication.
The sender might wish to change his private/public key pair from time to time for more secured communication.
 The sender may want to use different key pairs for different community of people such as friends, colleagues, etc.
The sender may want to use different key pairs for different community of people such as friends, colleagues, etc.
Note that the private/public key ring is stored only on the machine of the user who owns the key pairs, so that it is accessible to that user only.
15. How does PGP use the concept of trust and legitimacy?
Ans.: Like other protocols, PGP also makes use of certificates to authenticate public keys. However, the process is completely different. In PGP, no certification authority (CA) is involved; rather, anyone in the ring can sign a certificate for others in the ring. Thus, PGP certificates are not issued by any certification authority; rather, the users themselves are responsible for issuing certificates to each other. The entire working of PGP is based on the introducer trust, the certificate trust and the key legitimacy.
 Introducer (or producer) trust levels: Since there is no certification authority that the PGP users can trust, the users have to maintain a level of trust among each other. The introducer trust level
indicates the trustworthiness of the introducer (the user who issues certificates to other users). PGP defines three levels of trusts, namely, none, partial, and full. For example, user
Introducer (or producer) trust levels: Since there is no certification authority that the PGP users can trust, the users have to maintain a level of trust among each other. The introducer trust level
indicates the trustworthiness of the introducer (the user who issues certificates to other users). PGP defines three levels of trusts, namely, none, partial, and full. For example, user A can have full trust on user B, partial trust on users C and D and no trust on user E. It must be noted that there is no way in PGP to determine the trustworthiness of the introducer; it entirely depends on the user who makes an assessment of the trust to be assigned to the introducer.
 Certificate trust levels: When a user
Certificate trust levels: When a user A receives a certificate signed by the introducer, it assigns a level of trust to this certificate. Thus, the certificate trust level indicates the extent to which a PGP user can trust the certificate issued by an introducer. It is generally the same as that of the introducer trust level. For example, suppose B issues a certificate for E, and A receives that certificate, then A assigns a full level of trust to this certificate, as A fully trusts B. However, if A receives a certificate from E, then A can either discard this certificate or assign a zero level of trust to it, as A has no trust on E.
 Key legitimacy: This indicates the level of legitimacy of public key of a user. That is, the extent to which one can trust that a particular key is a valid key for a particular user. PGP defines certain weighted trust levels to determine the level of legitimacy of the key for the user. The higher the weight, the stronger the binding of the user ID to his or her key. For example, a weight of 0 indicates a nontrusted certificate, weight of ½ indicates a partially trusted certificate and, finally, a weight of 1 indicates a fully trusted certificate. For example,
Key legitimacy: This indicates the level of legitimacy of public key of a user. That is, the extent to which one can trust that a particular key is a valid key for a particular user. PGP defines certain weighted trust levels to determine the level of legitimacy of the key for the user. The higher the weight, the stronger the binding of the user ID to his or her key. For example, a weight of 0 indicates a nontrusted certificate, weight of ½ indicates a partially trusted certificate and, finally, a weight of 1 indicates a fully trusted certificate. For example, A can use E's public key because B has issued a certificate (with a trust level of 1) for E. However, A cannot use any certificate issued by E, as for A, E has a trust level of none. Thus, it is clear from our example that the legitimacy of the public key of a particular user does not depend on the trust level of that user; rather, it depends on the trust level of the introducer who has issued this certificate.
16. What is the structure of the key rings of PGP? Explain how messages are exchanged with the help of key rings.
Ans.: The structure of a private/public key ring can be represented as a table where each row represents one of the public/private key pairs owned by the user. Each row contains various entries, which are as follows:
 Timestamp: This field specifies the date and time when that particular private/public key pair was generated.
Timestamp: This field specifies the date and time when that particular private/public key pair was generated.
 Key ID: This field contains the least significant 64 bits of the public key for this entry. Since the user can have multiple public keys, this field helps in uniquely identifying each key.
Key ID: This field contains the least significant 64 bits of the public key for this entry. Since the user can have multiple public keys, this field helps in uniquely identifying each key.
 Public key: This field contains the public key portion of the pair.
Public key: This field contains the public key portion of the pair.
 Private key: This is an encrypted field that contains the private key portion of the pair.
Private key: This is an encrypted field that contains the private key portion of the pair.
 User ID: This field generally contains the e-mail address of the user. However, in some cases, the user may wish to associate different names with each pair or to reuse the same user ID.
User ID: This field generally contains the e-mail address of the user. However, in some cases, the user may wish to associate different names with each pair or to reuse the same user ID.
The public key ring contains the public keys of the other users who are known to this user. The fields of the public-key ring are explained as follows:
 Timestamp: This field contains the date and time when the entry was generated.
Timestamp: This field contains the date and time when the entry was generated.
 Key ID: This field contains the least significant 64 bits of the public key for this entry.
Key ID: This field contains the least significant 64 bits of the public key for this entry.
 Public key: This field contains the public key for this entry.
Public key: This field contains the public key for this entry.
 Producer trust: This field specifies the introducer level of trust. It can take one of the three values: none, partial or full.
Producer trust: This field specifies the introducer level of trust. It can take one of the three values: none, partial or full.
 Certificate(s): This field contains one or more certificates signed by other users for this user.
Certificate(s): This field contains one or more certificates signed by other users for this user.
 Certificate Trust(s): This field contains the trust level of certificates. If
Certificate Trust(s): This field contains the trust level of certificates. If A has signed a certificate for B, then the value in the certificate trust field for B is equal to the value in the producer trust field for A.
 Key legitimacy: This field stores a value that is computed on the basis of the value contained in the certificate trust field and the predefined weight for each certificate trust.
Key legitimacy: This field stores a value that is computed on the basis of the value contained in the certificate trust field and the predefined weight for each certificate trust.
 User ID: This field specifies the owner of this public key, and generally contains the e-mail address of the user. There may be more than one user IDs associated with a single public key.
User ID: This field specifies the owner of this public key, and generally contains the e-mail address of the user. There may be more than one user IDs associated with a single public key.
The general structure of private/public ring and public ring is shown in Figure 9.6. Both the private/public and public ring can be indexed by either User ID or Key ID.
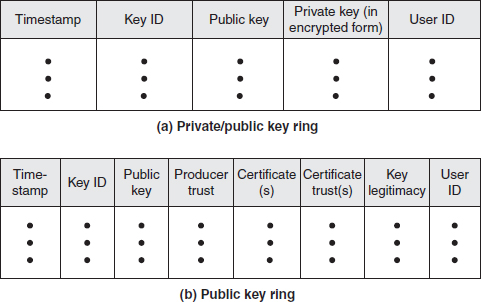
Figure 9.6 General Structure of Private/public and Public Ring
To understand the working of key rings, let us suppose that user A wants to send a message to many users and also wants to receive messages from the others. For this, A would have many pairs of private/public keys belonging to him or her and various public keys belonging to the other people with whom he or she wants to communicate. Now, when A wants to send a message to another person in the community, it needs to perform the following steps.
1. A signs the message digest using its private key. The private key of A is retrieved from the private/public key ring using the User ID field as an index.
2. A encrypts a newly created session key using the desired recipient's public key. The public key is retrieved from the public key ring using the User ID of the intended recipient as an index.
3. A encrypts the message and the signed digest using the newly created session key.
When A receives a message from another person in the community, it needs to perform the following steps.
1. A decrypts the session key using its private key. The private key of A is retrieved from the private/public key ring using the Key ID field included in the signature key component as an index.
2. A decrypts the message and the digest using the session key.
3. A verifies the digest using its public key. To retrieve the public key, the Key ID field included in the signature key component is used as an index.
17. What is the need of the Key ID field in the private/public and public key rings in PGP, if the public keys for a user are themselves unique?
Ans.: When a user (say, A) wants to send a message to another user (say, B), then it sends the message and digest encrypted with the session key K. The session key encrypted with the recipient's public key is sent along with the message. However, as in PGP, every user has multiple pairs of private/public keys, then, how does the recipient know which of its public keys has been used for encrypting the session key? One solution is to send the used public key of the recipient along with the message. This approach is fine; however, it results in wastage of space, as public keys are very long. Another solution is to attach a Key ID with each public key, which consists of its least significant 64 bits. The key ID is much shorter than the public key, and uniquely identifies each public key. Now, instead of sending the whole public key, the sender can transmit only the Key ID of the public key. Thus, the Key ID field is included in the private/public and public rings in PGP.
18. Discuss the general format of a PGP message.
Ans.: A PGP message consists of three components: a session key component, a signature and the message (see Figure 9.7). The entire block containing these components is generally encoded with radix-64 encoding. These components are discussed as follows:
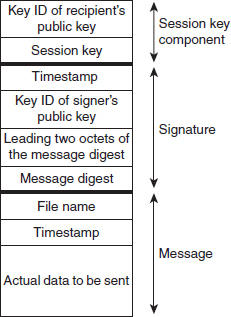
Figure 9.7 PGP message format
 Session key component: This component includes the session key and Key ID of the recipient's public key that the sender has used to encrypt the session key.
Session key component: This component includes the session key and Key ID of the recipient's public key that the sender has used to encrypt the session key.
 Signature component: This component includes the following fields.
Signature component: This component includes the following fields.
 Timestamp: This is 4-byte field that defines the time of creation of the signature.
Timestamp: This is 4-byte field that defines the time of creation of the signature.
 Key ID: This is an 8-byte field that contains the Key ID of the signer's public key. This enables the recipient to identify the public key to be used for decrypting the message digest.
Key ID: This is an 8-byte field that contains the Key ID of the signer's public key. This enables the recipient to identify the public key to be used for decrypting the message digest.
 Message digest: This field contains the 160-bit SHA-1 digest, which is computed over the timestamp of the signature along with the data portion of the message component. The inclusion of the timestamp safeguards against replay attacks. The message digest is signed by the sender using its private key.
Message digest: This field contains the 160-bit SHA-1 digest, which is computed over the timestamp of the signature along with the data portion of the message component. The inclusion of the timestamp safeguards against replay attacks. The message digest is signed by the sender using its private key.
 Leading two octets of message digest: This field contains the first 2 bytes of digest in plaintext. These 2 bytes are included as a kind of checksum. These bytes ensure that the recipient is using the correct public key to decrypt the message digest. The recipient compares the plaintext copy of these two octets with the first two octets of the decrypted digest. If they match, it is verified that the recipient is using the correct public key.
Leading two octets of message digest: This field contains the first 2 bytes of digest in plaintext. These 2 bytes are included as a kind of checksum. These bytes ensure that the recipient is using the correct public key to decrypt the message digest. The recipient compares the plaintext copy of these two octets with the first two octets of the decrypted digest. If they match, it is verified that the recipient is using the correct public key.
 Message component: This component contains the actual data to be transmitted. It also includes a filename and a timestamp that specifies the time of creation.
Message component: This component contains the actual data to be transmitted. It also includes a filename and a timestamp that specifies the time of creation.
19. How are PGP certificates different from X.509 certificates?
Ans.: Both PGP and X.509 certificates are standard security certificates. The main differences between PGP and X.509 are discussed in Table 9.3.
| PGP | X.509 |
|---|---|
| PGP certificates contain a self signature, and also support multiple signatures. The public key in a PGP certificate is associated with several fields, which are used to identify the key owner in different ways. | X.509 certificates contain only a single digital signature to verify the key's validity. Moreover, only one field is used for identifying the key owner. |
| PGP certificates can be created by a normal user; no CA is involved in the creation of certificates. The keys are managed by the users, and a user can validate another user. This process eventually results in a web of trust between groups of people. | X.509 certificates have to be issued by a certification authority. The keys here are managed by the CA only. |
| In PGP, multiple paths can exist from fully trusted or partially trusted authorities to any certificate. | In X.509, only a single path exists from the fully trusted authority (CA) to any certificate. |
| In PGP, the certificates can be revoked by the owner of the certificate or the revoker. | In X.509, the certificate can be revoked only by the issuer of the certificate, that is, the CA. |
20. Explain the S/MIME protocol.
Ans.: S/MIME (stands for secure/multipurpose Internet mail extension) is a protocol designed for e-mail that enhances the standard MIME protocol by providing the security features. The S/MIME is similar to PGP as far as IETF standards are concerned, however, it is assumed that, in future, S/MIME is most likely to be used for commercial and organizational purposes, while PGP will be used for personal e-mail security purpose. S/MIME uses the same standards that were used in MIME, along with a few security enhancements. The MIME overview and the S/MIME features are discussed in the following sections.
MIME Overview
MIME (stands for multipurpose Internet mail extensions) is a protocol that enables transferring non-ASCII data through e-mails, and thus, overcomes the limitations of SMTP (simple mail transfer protocol), which only allows sending text messages over the Internet. MIME converts non-ASCII messages to a 7-bit NVT (network virtual terminal) ASCII format at the sender's side. The converted message is then forwarded to the client message transfer agent (MTA), so that it can be sent over the Internet to the receiver. At receiver's side, the message is converted to its original format. MIME can also be used to send messages in different languages such as French, German, Chinese, etc. The structure of MIME defines five new headers that were included in the original e-mail header section. These headers are described as follows.
 MIME-Version: This header specifies the MIME version and tells the receiver that the sender is using MIME message format. The version number 1.1 is being used nowadays.
MIME-Version: This header specifies the MIME version and tells the receiver that the sender is using MIME message format. The version number 1.1 is being used nowadays.
 Content-Type: This header defines the type and subtype of the data used in the message body. The type of the data is followed by its subtype, separated by a slash, that is, type/subtype. Some of the types and their subtypes used by MIME are listed in Table 9.4.
Content-Type: This header defines the type and subtype of the data used in the message body. The type of the data is followed by its subtype, separated by a slash, that is, type/subtype. Some of the types and their subtypes used by MIME are listed in Table 9.4.
| Type | Subtype | Description |
|---|---|---|
| Text | Plain | Unformatted |
| HTML | HTML format | |
| Image | JPEG | Image is in JPEG format |
| GIF | Image is in GIF format | |
| Video | MPEG | Video is in MPEG format |
| Audio | Basic | Single-channel encoding of voice at 8 kHz |
 Content-Transfer-Encoding: This header defines the different methods used in encoding the messages into various formats so that it can be transmitted over a network. Some schemes used for encoding the message body are listed in Table 9.5.
Content-Transfer-Encoding: This header defines the different methods used in encoding the messages into various formats so that it can be transmitted over a network. Some schemes used for encoding the message body are listed in Table 9.5.
| Type | Description |
|---|---|
| 7-bit | NVT ASCII characters and short lines |
| 8-bit | Non-ASCII characters and short lines |
| Binary | Non-ASCII characters with unlimited length |
 Content-Id: This header uniquely identifies the message content.
Content-Id: This header uniquely identifies the message content.
 Content-Description: This header tells what the body of the message contains, that is, whether it contains picture, audio or video. It is an ASCII string that helps the receiver decide whether the message needs to be decoded.
Content-Description: This header tells what the body of the message contains, that is, whether it contains picture, audio or video. It is an ASCII string that helps the receiver decide whether the message needs to be decoded.
S/MIME Functionality
The basic functionality of S/MIME is similar to that of PGP, that is, it mainly supports digital signature and encryption of e-mail messages. However, apart from these basic functionalities, it also supports some other functions, which are as follows.
 Enveloped data: S/MIME supports enveloped data, which consists of the message containing any type of contents in encrypted form and the encryption key encrypted with receiver's public key.
Enveloped data: S/MIME supports enveloped data, which consists of the message containing any type of contents in encrypted form and the encryption key encrypted with receiver's public key.
 Signed data: This consists of the message digest encrypted using the sender's private key. S/MIME provides more confidentiality to the message by encoding the message and the signature using base64 encoding. This signed message can only be viewed by the receivers who have S/MIME capability.
Signed data: This consists of the message digest encrypted using the sender's private key. S/MIME provides more confidentiality to the message by encoding the message and the signature using base64 encoding. This signed message can only be viewed by the receivers who have S/MIME capability.
 Clear-signed data: This functionality is similar to the signed data and forms a digital signature of the message. The only difference is that, in this case, only the digital signature is encoded using base64 encoding. This allows the receivers to view the contents of the message even if they do not have S/MIME capability. However, they cannot verify the signature.
Clear-signed data: This functionality is similar to the signed data and forms a digital signature of the message. The only difference is that, in this case, only the digital signature is encoded using base64 encoding. This allows the receivers to view the contents of the message even if they do not have S/MIME capability. However, they cannot verify the signature.
 Signed and enveloped data: This is a mixture of the previously mentioned functions. In this case, S/MIME allows nesting of signed-only and encrypted-only entities, so that the encrypted data can be signed, and signed or clear-signed data can be encrypted.
Signed and enveloped data: This is a mixture of the previously mentioned functions. In this case, S/MIME allows nesting of signed-only and encrypted-only entities, so that the encrypted data can be signed, and signed or clear-signed data can be encrypted.
S/MIME Messages
S/MIME makes the MIME entity (such as a message or a part of it) secure either with a signature or with encryption, or both. Initially, a MIME entity is prepared according to the general rules for MIME message preparation. The MIME entity can either be the entire message, or a part of it (in case the content type is multipart). Then, the MIME entity along with the security-related data, such as algorithm identifiers and digital certificates, are processed by S/MIME. The output generated from this process is the PKCS (public key cryptography standard) object. The PKCS is now wrapped in MIME, and proper MIME headers are added to it.
To add security features such as digital signatures and encryption, S/MIME defines two new content types, which are listed in Table 9.6.
Table 9.6 S/MIME content types
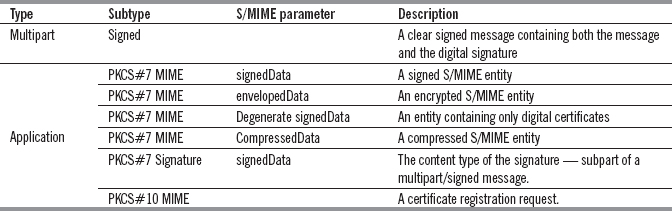
S/MIME Certificate Processing
S/MIME makes use of digital certificates that conform to the third version of X.509. The key-management scheme of S/MIME is a mixture of X.509 certification hierarchy and PGP's web of trust. As with the PGP model, S/MIME users are responsible for maintaining the certificates needed to verify the incoming signatures and for encrypting the outgoing messages, and as with X.509, only CAs are allowed to sign the certificates.
An S/MIME user performs three key-management functions, namely, key generation, registration and certificate storage and retrieval. In the key generation process, the user having administrative capabilities must be able to generate key pairs using DSS and Diffie-Hellman, and should be able to generate the key pairs using RSA. In the registration process, the user receives an X.509 digital certificate. To receive an X.509 certificate, the user has to first register its public key with the CA. The certificate storage and retrieval process deals with maintaining a local list of certificates, so that the users can retrieve their certificates to validate the incoming signatures and encrypt the outgoing messages. This list can be maintained either by the users or by some local administrative entity on behalf of the users.
S/MIME Enhanced Security Services
The S/MIME provides three enhanced security services, which are discussed as follows:
 Signed receipts: This is an acknowledgement message that is used to inform the sender about the delivery of the message. The entire message, including the original message and signature of the
sender, is signed by the receiver, and the new signature is appended to form a new S/MIME message.
Signed receipts: This is an acknowledgement message that is used to inform the sender about the delivery of the message. The entire message, including the original message and signature of the
sender, is signed by the receiver, and the new signature is appended to form a new S/MIME message.
 Security labels: Each signed object can also include a security label in the authenticated attributes. This security label basically includes information regarding the confidentiality (sensitivity) of the message being protected by S/MIME. In addition to confidentiality, the labels can also be used for access control (which users are authorized to access the object), for defining priority of the message (secret, confidential, restricted, etc.) or for defining role-based access (which category of users are allowed to see the information).
Security labels: Each signed object can also include a security label in the authenticated attributes. This security label basically includes information regarding the confidentiality (sensitivity) of the message being protected by S/MIME. In addition to confidentiality, the labels can also be used for access control (which users are authorized to access the object), for defining priority of the message (secret, confidential, restricted, etc.) or for defining role-based access (which category of users are allowed to see the information).
 Secure mailing lists: When a sender wants to send a message to a recipient, he or she needs to encrypt the message using recipient's public key. In case the same message needs to be sent to several recipients, then the sender has to encrypt the message with every recipient's public key before sending it to these recipients. This is very time-consuming task. To simplify this process, S/MIME provides a Mail List Agent (MLA), who is responsible for performing recipient-specific encryption of the message for each recipient. The creator of the message needs to send the original message to MLA, only once, encrypted with the MLA's public key, and the rest is done by MLA itself.
Secure mailing lists: When a sender wants to send a message to a recipient, he or she needs to encrypt the message using recipient's public key. In case the same message needs to be sent to several recipients, then the sender has to encrypt the message with every recipient's public key before sending it to these recipients. This is very time-consuming task. To simplify this process, S/MIME provides a Mail List Agent (MLA), who is responsible for performing recipient-specific encryption of the message for each recipient. The creator of the message needs to send the original message to MLA, only once, encrypted with the MLA's public key, and the rest is done by MLA itself.
21. Give an overview of IP security along with its applications and benefits.
Ans.: The Internet community has developed many application-specific security protocols such as Kerberos (for client/server), PGP and S/MIME (for electronic mail) and many others. These protocols provide security only at higher network layers, such as the application and transport layer. However, some applications such as routing protocols that use IP services need security service at the network layer or Internet protocol (IP) layer. To provide security at the IP layer, the IETF developed a collection of protocols referred to as IP security (IPSec). Before IPSec was initiated, the IP packets were prone to security failure. The data in the IP packets were in plaintext form, which allowed anyone to access or change the contents of the packets during transmission.
The overall idea of IPSec protocol is to encrypt and seal the transport and application layer during transmission, and also to provide integrity protection in the Internet layer itself. IPSec provides three security functions, namely, authentication, confidentiality and key management. Authentication ensures that the packets are arriving from the actual source as specified in the packet header. It also ensures that the packet has not been altered during transmission. The confidentiality function allows two communicating nodes to transfer messages in an encrypted form in order to prevent any third-party intervention. The key management provides a platform for exchanging keys in a secured manner. All these security measures are incorporated in both the versions of IP, namely, IP version 4 (IPv4) and IP version 6 (IPv6).
The IPSec enables secure communication across different types of networks such as LANs and WANs. It also secures the Internet. The applications of IPSec are discussed as follows:
 Secure remote access over the Internet: An end user using IPSec protocols can make a local call to an Internet Service Provider (ISP) and request it to provide a secure access to a company network. This reduces travelling cost and time wastage of employees and telecommuters.
Secure remote access over the Internet: An end user using IPSec protocols can make a local call to an Internet Service Provider (ISP) and request it to provide a secure access to a company network. This reduces travelling cost and time wastage of employees and telecommuters.
 Enhancing electronic commerce security: Though many e-commerce sites provide in-built security services, the use of IPSec further increases the level of security.
Enhancing electronic commerce security: Though many e-commerce sites provide in-built security services, the use of IPSec further increases the level of security.
 Secure branch office connectivity over the Internet: IPSec can be used to create a secured virtual private network over the Internet or over a public WAN, connecting all the branches of a company. This will save the cost of creating a private network that needs expensive leased lines.
Secure branch office connectivity over the Internet: IPSec can be used to create a secured virtual private network over the Internet or over a public WAN, connecting all the branches of a company. This will save the cost of creating a private network that needs expensive leased lines.
 Establishing extranet and intranet connectivity with partners: IPSec can be used to make secure connections with other organizations, since it addresses all the three security issues: authentication, confidentiality and key management.
Establishing extranet and intranet connectivity with partners: IPSec can be used to make secure connections with other organizations, since it addresses all the three security issues: authentication, confidentiality and key management.
IPSec has got many advantages, which are as follows:
 IPSec is very transparent to end users. There is no need to provide any kind of training to the users. It also does not require to issue or revoke keys to and from the users.
IPSec is very transparent to end users. There is no need to provide any kind of training to the users. It also does not require to issue or revoke keys to and from the users.
 When IPSec is implemented in a firewall or router, it provides more security as it becomes the only entry/exit point for all the traffic. However, the internal traffic does not have to use IPSec and is, thus, free from the overhead of any security-related processing.
When IPSec is implemented in a firewall or router, it provides more security as it becomes the only entry/exit point for all the traffic. However, the internal traffic does not have to use IPSec and is, thus, free from the overhead of any security-related processing.
 Since IPSec is implemented at the network layer, there is no need to make any changes at the upper layers such as application and transport layer.
Since IPSec is implemented at the network layer, there is no need to make any changes at the upper layers such as application and transport layer.
 IPSec can provide security to individual users also. Individuals can set up secure virtual sub-networks within an organization for sensitive applications. These types of connections are useful for offsite workers.
IPSec can provide security to individual users also. Individuals can set up secure virtual sub-networks within an organization for sensitive applications. These types of connections are useful for offsite workers.
22. Write a short note on transport and tunnel mode.
Ans.: IPSec operates in two different modes, namely, transport mode and tunnel mode. The transport mode is used to provide protection mainly for the upper layer protocols. In this mode, IPSec protects the packets coming from the transport layer to the network layer. That is, it only protects the IP layer payload and not the IP header. It does not protect the whole IP packet. In this mode, the IPSec header and IPSec trailer are added to the packet coming from the transport layer, which becomes the IP payload in network layer, and later the IP header is added to the payload. This mode is used for secured host-to-host communication. The sender authenticates and/or encrypts the payload received from the transport layer using IPSec. The receiver verifies the authenticity and/or decrypts the IP packet using IPSec and forwards it to the transport layer.
The tunnel mode is used to provide security to the entire IP packet. Here, the IP packet is totally protected, including the IP header. Also, a new IP header is added to the protected packet. The tunnel mode is used when either or both of the communicating parties are security gateways, such as routers. That is, tunnel mode provides secure communication between two routers, or between a router and a host or between a host and a router. The packets transmitting from sender to receiver are protected from intrusion as if the packets pass through an imaginary tunnel.
The main difference between the transport mode and the tunnel mode is that, in the former case, the IPSec layer comes between the transport layer and the network layer. However, in case of tunnel mode, the information flows from the network layer to the IPSec layer and then back to the network layer.
23. Write a short note on IPSec RFC documents.
Ans.: In 1995, the Internet Engineering Task Force (IETF) published several security standards related to IPSec in the form of RFC documents. The most important of these are RFCs 2401, 2402, 2406, and 2408. RFC 2401 gives an overview of security architecture, RFC 2402 contains a description of a packet authentication extension to IPv4 and IPv6, RFC 2406 consists of a description of a packet encryption extension to IPv4 and IPv6, and finally RFC 2408 includes specification of key management capabilities. In addition to these four RFCs, several additional drafts have been published by IP security Protocol Working Group set up by IETF. These documents are divided into seven groups, as shown in Figure 9.8.
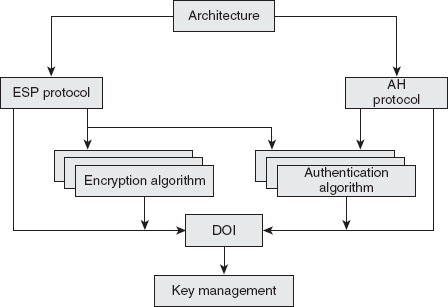
Figure 9.8 Overview of IPSec Document
 Architecture: This includes the general concepts, requirements for security, definitions and the mechanisms needed for defining IP security.
Architecture: This includes the general concepts, requirements for security, definitions and the mechanisms needed for defining IP security.
 Encapsulating security payload (ESP): This includes the packet format and issues related to the use of ESP. The issues deal with the encryption of packets by ESP and, occasionally, with authentication.
Encapsulating security payload (ESP): This includes the packet format and issues related to the use of ESP. The issues deal with the encryption of packets by ESP and, occasionally, with authentication.
 Authentication Header (AH): This includes the packet format and issues related to the use of AH for authentication of packets.
Authentication Header (AH): This includes the packet format and issues related to the use of AH for authentication of packets.
 Encryption algorithm: This is a set of documents describing the use of various encryption algorithms for ESP.
Encryption algorithm: This is a set of documents describing the use of various encryption algorithms for ESP.
 Authentication algorithm: This is a set of documents specifying the use of authentication algorithms for AH. It also deals with the authentication option used in ESP.
Authentication algorithm: This is a set of documents specifying the use of authentication algorithms for AH. It also deals with the authentication option used in ESP.
 Key management: This is a set of documents describing the various key management schemes.
Key management: This is a set of documents describing the various key management schemes.
 Domain of interpretation (DOI): This contains the values that are used to relate all the documents with each other. The values include identifiers for the authentication and encryption algorithms that have already been approved, and operational parameters such as key lifetime.
Domain of interpretation (DOI): This contains the values that are used to relate all the documents with each other. The values include identifiers for the authentication and encryption algorithms that have already been approved, and operational parameters such as key lifetime.
24. Name the two protocols defined by IPSec.
Ans.: The two protocols defined by IPSec are the Authentication Header (AH) protocol and the Encapsulating Security Payload (ESP) protocol. These protocols provide the authentication and/or encryption for the packets at the IP level.
25. Explain the Authentication Header (AH) protocol.
Ans.: The Authentication Header (AH) protocol is used to provide source authentication, and also to ensure the integrity of the payloads being carried in the IP packets.
 The authentication feature allows the receiver to authenticate the sender, and accept or reject packets, accordingly. In addition, it prevents the address spoofing attacks.
The authentication feature allows the receiver to authenticate the sender, and accept or reject packets, accordingly. In addition, it prevents the address spoofing attacks.
 The integrity feature ensures that the contents of the IP packets are not altered during transmission.
The integrity feature ensures that the contents of the IP packets are not altered during transmission.
This protocol is based on the message authentication code (MAC), which implies that the two parties must share a secret key. First, a message digest is created with the help of a hash function and a symmetric key. The message digest is then inserted into the AH. This AH is finally placed in the appropriate location as per the mode used (transport or tunnel). The AH format is shown in the Figure 9.9.
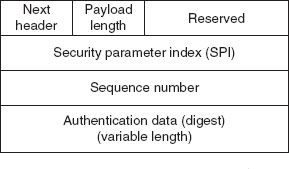
Figure 9.9 Authentication Header format
The various fields of the AH are discussed in the following:
 Next header: This is an 8-bit field that specifies
Next header: This is an 8-bit field that specifies
the type of header immediately following this
header. If ESP header follows the AH, this field contains the value 50, and if another AH follows
this AH, it contains the value 51.
 Payload length: This is an 8-bit field that specifies the length of the AH in 32-bit words (in 4-byte multiples) minus 2. For example, if the length of the authentication data field is 96 bits (or three 32-bit words), then with a three-word fixed length, we have a total of six words in the header. Thus, the value of this field is 4.
Payload length: This is an 8-bit field that specifies the length of the AH in 32-bit words (in 4-byte multiples) minus 2. For example, if the length of the authentication data field is 96 bits (or three 32-bit words), then with a three-word fixed length, we have a total of six words in the header. Thus, the value of this field is 4.
 Reserved field: This is a 16-bit field that has been kept reserved for future use.
Reserved field: This is a 16-bit field that has been kept reserved for future use.
 Security parameter index (SPI): This is a 32-bit field that uniquely identifies the security associations (discussed later) for the traffic to which the IP datagram belongs. It plays the role of a virtual circuit identifier. This field is used in combination with the source and destination addresses, as well as the IPSec protocol used (AH or ESP).
Security parameter index (SPI): This is a 32-bit field that uniquely identifies the security associations (discussed later) for the traffic to which the IP datagram belongs. It plays the role of a virtual circuit identifier. This field is used in combination with the source and destination addresses, as well as the IPSec protocol used (AH or ESP).
 Sequence number: This is a 32-bit field that contains a monotonically increasing number (a counter) that specifies the ordering of the IP datagrams. The sequence number is capable of preventing the replay attacks. The sender must always transmit this field, but the receiver need not always act upon it. The first packet transmitted has a sequence number of 1, and once it reaches the value 232, a new connection must be established and the sender's and receiver's counter must be reset.
Sequence number: This is a 32-bit field that contains a monotonically increasing number (a counter) that specifies the ordering of the IP datagrams. The sequence number is capable of preventing the replay attacks. The sender must always transmit this field, but the receiver need not always act upon it. The first packet transmitted has a sequence number of 1, and once it reaches the value 232, a new connection must be established and the sender's and receiver's counter must be reset.
 Authentication data: This is a variable-length field that contains the authentication data, called the Integrity Check Value (ICV), for the datagram. For IPv4 datagrams, this value must be an integral multiple of 32, and for IPv6, this value must be an integral multiple of 64. The ICV is generated by applying a hash function to the whole IP datagram. The fields that are changed during transmission are not included while applying the hash function.
Authentication data: This is a variable-length field that contains the authentication data, called the Integrity Check Value (ICV), for the datagram. For IPv4 datagrams, this value must be an integral multiple of 32, and for IPv6, this value must be an integral multiple of 64. The ICV is generated by applying a hash function to the whole IP datagram. The fields that are changed during transmission are not included while applying the hash function.
26. How does the AH protocol prevent the replay attack?
Ans.: The sequence number field in the IPSec AH protocol is designed to prevent the replay attacks. Initially, the value of this field is set to 1. Now, each time the sender sends a packet to the receiver over the same security association (or connection), the value is incremented by one. When the value of the sequence reaches 232, it is not set back to 1 in order to prevent the use of the same sequence numbers again. Rather, a new connection with a new secret key must be established between the sender and the receiver.
Since IP is connectionless and unreliable, it does not guarantee that all the packets will be delivered and that the packets will be delivered in the correct sequence. To ensure this, the IPSec authentication document prescribes the receiver to implement a window of size W. The default value of W is 64. The
right edge of the window specifies the highest sequence number N of a valid packet, received so far. After receiving a packet, the receiver takes one of the following actions, depending on the sequence number of the packet:
 The receiver determines whether the received packet is new, and falls in the range of the window, that is, if its sequence number lies between
The receiver determines whether the received packet is new, and falls in the range of the window, that is, if its sequence number lies between N−W+1 and N. If both the conditions are satisfied, then the receiver checks the authenticity of the packet. If the packet is authenticated, the corresponding slot in the window is marked.
 If the sequence number of the newly received packet is greater than
If the sequence number of the newly received packet is greater than N, and if the packet is authenticated, then the receiver advances the window and makes this new sequence number the right edge of the window. Finally, the corresponding slot in the window is marked.
 If the received packet is to the left of the window, that is, its request number is less than
If the received packet is to the left of the window, that is, its request number is less than N−W, or if it is not authenticated, the receiver discards the packet and triggers an auditable event.
The third action prevents the replay attacks, because if the receiver receives a packet with a sequence number less than N−W, then he or she concludes that some attacker is attempting to impersonate the sender and resend an already received packet.
27. Describe how AH is used in transport and tunnel modes in IPSec protocol.
Ans.: The AH protocol can operate in both transport mode and tunnel mode. In transport mode, authentication is provided directly between the server and client workstations. The server and client workstations can be present either on the same network or on different networks. In tunnel mode, a workstation present on a remote network authenticates itself to the corporate firewall. Let us have a look at the scope of authentication provided by AH and the location of AH for the two modes. These two modes further vary for IPv4 and IPv6.
AH Transport Mode
In transport mode AH, when IPv4 packet is used, the AH is inserted after the original IP header but before the IP payload. The entire packet except the mutable fields of IPv4 is authenticated. On the other hand, when IPv6 is used, the AH is inserted after the base header and the hop-by-hop, routing and fragment extension headers. However, the destination options extension header can be placed either before the AH or after it, depending on the desired semantics. The authentication covers the entire IPv6 packet, except the mutable fields. The AH transport mode for both IPv4 and IPv6 packets is shown in Figure 9.10.
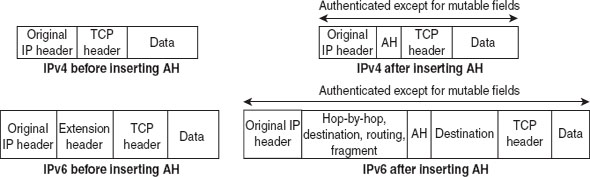
Figure 9.10 Transport mode AH
AH Tunnel Mode
In the tunnel mode AH, a new outer IP header is inserted into the packet, and the AH is inserted in between the original IP header and the new outer IP header. The addresses of the original source and destination are included in the inner IP header, while the addresses of firewalls or other security gateways are included in the new outer IP header. AH protects the entire inner IP packet, including the inner IP header. The new outer IP header is also protected, except for the mutable and unpredictable fields. The AH tunnel mode for both IPv4 and IPv6 packets is shown in Figure 9.11.

Figure 9.11 Tunnel mode AH
28. Explain the ESP protocol.
Ans.: The ESP protocol provides confidentiality and integrity of the messages. Optionally, this protocol can also provide an authentication service. The ESP packet format (containing a header and a trailer) is made up of seven fields (see Figure 9.12). These fields are discussed in the following text:
 Security parameters index (SPI): This is a 32-bit field that uniquely identifies the security associations for traffic to which the datagram belongs. It is used in combination with the source and destination IP addresses, as well as the security protocol used (AH or ESP). The SPI value ranges from 1 to 255, and these values have been reserved by the Internet Assigned Numbers Authority (IANA) for future use.
Security parameters index (SPI): This is a 32-bit field that uniquely identifies the security associations for traffic to which the datagram belongs. It is used in combination with the source and destination IP addresses, as well as the security protocol used (AH or ESP). The SPI value ranges from 1 to 255, and these values have been reserved by the Internet Assigned Numbers Authority (IANA) for future use.
 Sequence number: This is a 32-bit field that contains a number that increases monotonically. Initially, counter of both the sender and receiver is set to zero. This field prevents the replay
attacks similar to the AH. The sender must always transmit the field, but the receiver has the freedom to ignore it.
Sequence number: This is a 32-bit field that contains a number that increases monotonically. Initially, counter of both the sender and receiver is set to zero. This field prevents the replay
attacks similar to the AH. The sender must always transmit the field, but the receiver has the freedom to ignore it.
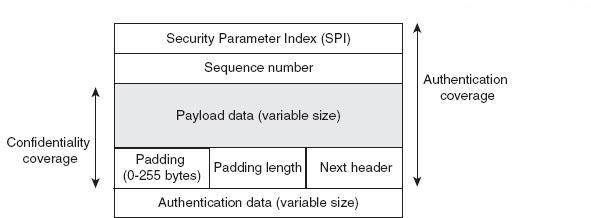
Figure 9.12 IPSec ESP format
 Payload data: This is a variable-length field that contains the transport-layer segment (transport mode) or IP packet (tunnel mode), which is protected using an encryption mechanism.
Payload data: This is a variable-length field that contains the transport-layer segment (transport mode) or IP packet (tunnel mode), which is protected using an encryption mechanism.
 Padding (0–255 bytes): This field contains the padding bits, if any. These bits are mainly used in encryption algorithms for expanding the plaintext to the required length. These can also be used for right-aligning the padding length and next header fields within the 32-bit word. This field also ensures that the ciphertext is an integer multiple of 32 bits.
Padding (0–255 bytes): This field contains the padding bits, if any. These bits are mainly used in encryption algorithms for expanding the plaintext to the required length. These can also be used for right-aligning the padding length and next header fields within the 32-bit word. This field also ensures that the ciphertext is an integer multiple of 32 bits.
 Padding length: This is an 8-bit field that indicates the number of bytes padded in the previous field. It can have a value between 0 and 255. A zero value indicates the absence of any padding bytes. This field is mandatory.
Padding length: This is an 8-bit field that indicates the number of bytes padded in the previous field. It can have a value between 0 and 255. A zero value indicates the absence of any padding bytes. This field is mandatory.
 Next header: This is an 8-bit field that indicates the type of data contained in the payload data field by identifying the first header in that payload (e.g. an upper layer protocol such as TCP in IPv4 and an extension header in IPv6). This field is mandatory.
Next header: This is an 8-bit field that indicates the type of data contained in the payload data field by identifying the first header in that payload (e.g. an upper layer protocol such as TCP in IPv4 and an extension header in IPv6). This field is mandatory.
 Authentication data: This is a variable-length field that contains the Integrity Check Value (ICV). The ICV value is computed by subtracting the authentication data field from the length of the ESP packet. The authentication data must always be an integral multiple of 32-bit words.
Authentication data: This is a variable-length field that contains the Integrity Check Value (ICV). The ICV value is computed by subtracting the authentication data field from the length of the ESP packet. The authentication data must always be an integral multiple of 32-bit words.
29. Describe the transport and tunnel mode of ESP.
Ans.: As with the AH protocol, ESP can also operate in transport and tunnel modes. Considering both IPv4 and IPv6 packets, the working of ESP in transport and tunnel modes is explained in the following:
Transport Mode ESP
The ESP in the transport mode is used to encrypt and optionally authenticate the data carried by IP. In case of IPv4 packets, the ESP header is inserted between the original IP header and transport-layer header (such as TCP, UDP and ICMP). An ESP trailer, consisting of padding, padding length and next header fields, is also placed after the IP packet (see Figure 9.13). If authentication is also used, the ESP authentication data field is also added at the end. The encryption is performed at the entire transport level segment, including the ESP trailer. The ciphertext and the ESP header are then authenticated.
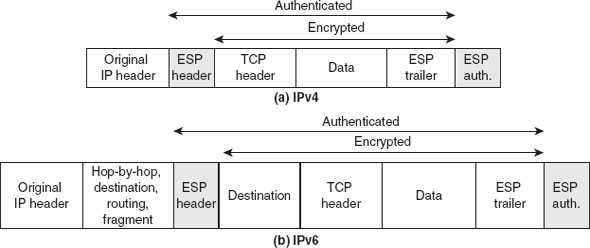
Figure 9.13 Transport mode ESP
In case of IPv6, the ESP header is inserted after the base header and the hop-by-hop, routing and fragment extension headers. Depending on the semantics, the destination options extension header can be inserted either before or after the ESP header. Here, the transport-level segment, the ESP trailer and the destination options extension header (if present) are encrypted, whereas the ciphertext and the ESP header are authenticated.
The operation of ESP transport mode is summarized as follows:
1. At the sender's end, the IP packet is formed by encrypting the plaintext of data containing the ESP trailer and the entire transport-layer segment (TCP header plus data): The authentication can also be added to the IP packet if this option is selected.
2. The packet is transmitted to the destination. The routers falling in the route examine and process only the IP header and the plaintext IP extension headers (if present) and not the ciphertext.
3. When the IP packet is received by the destination, the IP header and the plaintext IP extension headers are processed. After this, the destination decrypts the rest of the packet based on SPI in the ESP header in order to retrieve the plaintext transport layer segment.
Tunnel Mode ESP
In tunnel mode ESP, the entire IP packet is encrypted. The ESP header is prefixed to the packet, and the packet is then encrypted including the ESP trailer (see Figure 9.14). In this mode, the entire block (ESP header, ciphertext and authentication data, if present) is encapsulated with a new IP header because the original IP header contains the destination address and possibly intermediate routing information and, thus, cannot be transmitted as it is. Therefore, a new IP header is needed that will contain the necessary information for routing and not for traffic analysis.
The difference between transport mode ESP and tunnel mode ESP is that the former is used to protect connections between two hosts supporting the ESP feature, while the latter is suitable for protecting connections in configurations when some sort of security gateway or firewall is used. The encryption process in the tunnel mode involves only the external hosts and security gateways. The hosts on the internal network are not involved in this process, thus relieving them from the extra burden of encryption. This makes the key distribution task simpler, as lesser number of keys would be required, and prevents traffic analysis based on the ultimate destination.
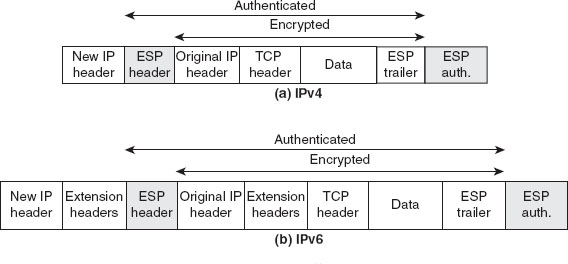
Figure 9.14 Tunnel Mode ESP
The operation of the ESP tunnel mode is summarized as follows.
1. At the sender's end, the inner IP packet is prepared using the destination address of the target host on the internal network. The ESP header is prepended to the packet. The packet and ESP trailer are then encrypted, and authentication data is added (if required) to form a block. The block is encapsulated with a new IP header that consists of the base header and some other extension headers such as routing and hop-by-hop options. This forms the outer IP packet, which contains the destination address of a firewall.
2. The outer IP packet is forwarded to the destination firewall. The routers falling in the route examine and process only the IP header and the plaintext IP extension headers (if present) and not the ciphertext.
3. At the receiver's end (i.e., firewall), the IP header and the plaintext IP extension headers are processed once again by the destination firewall. The ciphertext is then decrypted on the basis of SPI in the ESP header to recover the plaintext inner packet.
4. The inner packet is routed through zero or more routers in the internal network to reach the destination host.
30. Explain the Internet Key Exchange protocol and security association.
Ans.: Internet Key Exchange (IKE) is another supporting protocol that is used for the key management procedures in IPSec. It is the first phase of IPSec, where the cryptographic algorithms and keys to be later used by AH and ESP are decided. After the IKE phase, actual AH and ESP operations are carried over. The output of the IKE phase is Security Association (SA), which is a logical relationship agreement between the sender and receiver that allows both the communication parties to agree upon some factors such as IPSec protocol version in use, mode of operation (transport or tunnel mode), cryptographic algorithms and keys, lifetime of keys, etc.
The main objective of IKE is to build an SA between the sender and the receiver, which is further used by AH and ESP for their actual operation. Note that in case both AH and ESP are in use, then each communicating party requires two sets of SA: one for AH and other for ESP. Moreover, SA allows only one-way communication, and hence, the communicating parties require two more sets of SA; one for incoming messages and other for outgoing messages. Thus, in total, they require four sets of SA, if both AH and ESP are in use.
31. What are the services provided by IPSec?
Ans.: The services provided by IPSec are as follows:
 Access control
Access control
 Connectionless integrity
Connectionless integrity
 Data origin authentication
Data origin authentication
 Rejection of replayed packets
Rejection of replayed packets
 Confidentiality
Confidentiality
 Limited traffic flow confidentiality
Limited traffic flow confidentiality
The AH and ESP protocols of IPSec are responsible for providing some or all of these services. The AH protocol provides the first four services, that is, access control, connectionless integrity, data origin authentication and rejection of replayed packets. However, for ESP protocol, there are two cases, which are as follows:
 If the ESP protocol allows encryption only, then it provides access control, rejection of replayed packets, confidentiality and limited traffic flow confidentiality.
If the ESP protocol allows encryption only, then it provides access control, rejection of replayed packets, confidentiality and limited traffic flow confidentiality.
 If the ESP protocol allows both encryption and authentication, then it provides all these services.
If the ESP protocol allows both encryption and authentication, then it provides all these services.
32. Describe the features of Oakley algorithm used for key determination in IPSec.
Ans.: The Oakley algorithm is a key exchange protocol developed by Hilarie Orman. It is based on Diffie-Hellman algorithm, and is designed to retain the advantages of Diffie-Hellman while overcoming its limitations. Oakley is a free-formatted protocol, in the sense that it does not define any specific format for the message to be transmitted. It also provides more security than Diffie-Hellman algorithm. There are five features in Oakley algorithm that are used for key determination. These features are discussed in the following text:
 The clogging attack encountered in the Diffie-Hellman algorithm is removed in Oakley using the cookie mechanism. In this attack, the victim's system is clogged with useless work as it remains busy in generating secret keys for forged public keys sent by the intruder. In cookie exchange mechanism, a pseudo-random number, called a cookie, is generated by applying a hash function (such as MD5) over the source and destination address, the UDP source and destination ports, and a locally generated secret value. The cookie is sent from each side in the initial message, which is acknowledged by the other side. This acknowledgement must be repeated in the first message of the Diffie-Hellman key exchange. If the source address was forged, the intruder gets no answer. Thus, the intruder can only force a user to generate acknowledgements and not to perform useless calculations.
The clogging attack encountered in the Diffie-Hellman algorithm is removed in Oakley using the cookie mechanism. In this attack, the victim's system is clogged with useless work as it remains busy in generating secret keys for forged public keys sent by the intruder. In cookie exchange mechanism, a pseudo-random number, called a cookie, is generated by applying a hash function (such as MD5) over the source and destination address, the UDP source and destination ports, and a locally generated secret value. The cookie is sent from each side in the initial message, which is acknowledged by the other side. This acknowledgement must be repeated in the first message of the Diffie-Hellman key exchange. If the source address was forged, the intruder gets no answer. Thus, the intruder can only force a user to generate acknowledgements and not to perform useless calculations.
 The Oakley algorithm allows two parties to negotiate a group for specifying global parameters of Diffie-Hellman key exchange. Oakley supports the use of different groups for the Diffie-Hellman key exchange, where each group specifies the two global parameters (one is
The Oakley algorithm allows two parties to negotiate a group for specifying global parameters of Diffie-Hellman key exchange. Oakley supports the use of different groups for the Diffie-Hellman key exchange, where each group specifies the two global parameters (one is p, a large prime number and second is q, a primitive root of p), and the identity of the Diffie-Hellman algorithm. The present specification includes five groups, which are as follows:
 Modular exponentiation with a 768-bit modulus
Modular exponentiation with a 768-bit modulus
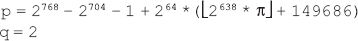
 Modular exponentiation with a 1024-bit modulus
Modular exponentiation with a 1024-bit modulus
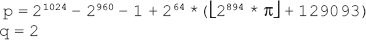
 Modular exponentiation with a 1536-bit modulus
Modular exponentiation with a 1536-bit modulus
– Parameters to be determined
 Elliptic curve group over 2155
Elliptic curve group over 2155
– Generator (hexadecimal): X = 7B, Y = 1C8.
– Elliptic curve parameters (hexadecimal): A = 0, Y = 7338F
 Elliptic curve group over 2185
Elliptic curve group over 2185
– Generator (hexadecimal): X = 18, Y = D
– Elliptic curve parameters (hexadecimal): A = 0, Y = 1EE9
 The Oakley algorithm prevents replay attacks by using nonces. The nonce is a pseudo-random number that is generated locally. Nonces are included in response messages, and are encrypted during certain portion of the exchange to secure their use.
The Oakley algorithm prevents replay attacks by using nonces. The nonce is a pseudo-random number that is generated locally. Nonces are included in response messages, and are encrypted during certain portion of the exchange to secure their use.
 The Oakley algorithm facilitates the exchange of Diffie-Hellman public key values (discussed in Chapter 5).
The Oakley algorithm facilitates the exchange of Diffie-Hellman public key values (discussed in Chapter 5).
 The Oakley algorithm authenticates the Diffie-Hellman exchange to prevent man-in-the-middle attacks. It can apply various authentication mechanisms such as digital signatures, public-key encryption and symmetric-key encryption on some important parameters such as user IDs and nonces to authenticate the key exchange.
The Oakley algorithm authenticates the Diffie-Hellman exchange to prevent man-in-the-middle attacks. It can apply various authentication mechanisms such as digital signatures, public-key encryption and symmetric-key encryption on some important parameters such as user IDs and nonces to authenticate the key exchange.
33. Explain the header format for an ISAKMP message.
Ans.: Internet Security Association and Key Management Protocol (ISAKMP) is designed to carry messages for Internet key exchange in IPSec. It defines procedures and formats for establishing, maintaining and deleting information regarding security associations. An ISAKMP message consists of an ISAKMP header followed by one or more payloads. This entire block is encapsulated inside a transport segment (such as a TCP segment). The header format for an ISAKMP message is shown in Figure 9.15. It consists of the following fields.

Figure 9.15 ISAKMP header format
 Initiator cookie: This is a 64-bit field
Initiator cookie: This is a 64-bit field
defining the cookie of the entity that initiates
the SA establishment, notification or deletion.
 Responder cookie: This is also a 64-bit field defining the cookie of the entity responding to the initiator. This field contains the value 0 in the first message sent by the initiator.
Responder cookie: This is also a 64-bit field defining the cookie of the entity responding to the initiator. This field contains the value 0 in the first message sent by the initiator.
 Next payload: This is an 8-bit field indicating the type of the first payload of the message.
Next payload: This is an 8-bit field indicating the type of the first payload of the message.
 Major version: This is a 4-bit field indicating the major ISAKMP version as used in the current exchange. The current value of this field is 1.
Major version: This is a 4-bit field indicating the major ISAKMP version as used in the current exchange. The current value of this field is 1.
 Minor version: This is also a 4-bit field indicating the minor ISAKMP version as used in the current exchange. The current value of this field is 0.
Minor version: This is also a 4-bit field indicating the minor ISAKMP version as used in the current exchange. The current value of this field is 0.
 Exchange type: This is an 8-bit field indicating the type of exchange that is being carried by the ISAKMP packets.
Exchange type: This is an 8-bit field indicating the type of exchange that is being carried by the ISAKMP packets.
 Flags: This is an 8-bit field indicating the specific set of options for this ISAKMP exchange. Each bit in this field defines a single option. So far, only 3 bits have been defined, which are as follows.
Flags: This is an 8-bit field indicating the specific set of options for this ISAKMP exchange. Each bit in this field defines a single option. So far, only 3 bits have been defined, which are as follows.
 Encryption bit is set to 1, if all the payloads following the header are encrypted using the encryption algorithm for this SA.
Encryption bit is set to 1, if all the payloads following the header are encrypted using the encryption algorithm for this SA.
 Commit bit is set to 1 to ensure that the encrypted packet is not received until the SA is established.
Commit bit is set to 1 to ensure that the encrypted packet is not received until the SA is established.
 Authentication bit is set to 1 to ensure that the rest of the payload, which is not encrypted, is still authenticated for integrity.
Authentication bit is set to 1 to ensure that the rest of the payload, which is not encrypted, is still authenticated for integrity.
 Message ID: This is a 32-bit field specifying a unique ID for this message.
Message ID: This is a 32-bit field specifying a unique ID for this message.
 Message length: This is a 32-bit field specifying the total length of the packet (including the header and all payloads) in octets.
Message length: This is a 32-bit field specifying the total length of the packet (including the header and all payloads) in octets.
34. What is SSL? Discuss its architecture.
Ans.: The Secure Socket Layer (SSL) protocol was developed by Netscape Corporation in 1994 to provide exchange of information between a web browser and a web server in a secure manner. As with other protocols, its main aim is to provide entity authentication, message integrity and confidentiality. SSL is an additional layer located between the application layer and the transport layer of the TCP/IP protocol suite. All the major web browsers support SSL. It comes in three versions: 2, 3 and 3.1. Among these, version 3, which was released in 1995, is the most popular version.
SSL architecture
SSL is not a single protocol; rather, it is two layers of protocols, as shown in Figure 9.16. The higher-layer protocols include Handshake protocol, Change Cipher Spec protocol and Alert protocol. These three protocols are defined as part of SSL, and are used in the SSL management process. The lower layer includes the SSL Record protocol, which is used for providing various basic security services to the higher-layer protocols. HTTP, which enables the web browser to interact with the web server, can work on the top of SSL.
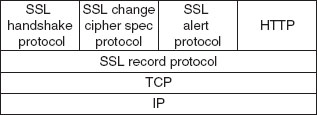
Figure 9.16 SSL Architecture
These protocols are discussed as follows:
 SSL Record protocol: This protocol acts as a carrier. That is, it is used for carrying the messages from the higher-layer protocols as well as data coming from the application layer. It receives the data to be transmitted from the application layer, and operates on it as follows:
SSL Record protocol: This protocol acts as a carrier. That is, it is used for carrying the messages from the higher-layer protocols as well as data coming from the application layer. It receives the data to be transmitted from the application layer, and operates on it as follows:
1. Fragmentation: The data is first divided into the blocks of 214 bytes or less.
2. Compression: This is an optional phase in which each fragment of data is compressed using one of the lossless compression techniques agreed upon between the client and server.
3. Message integrity: A keyed-hash function is applied on the compressed data to compute a message authentication code (MAC). This ensures the integrity of the message.
4. Confidentiality: The original data and the MAC are encrypted using symmetric-key cryptography to ensure confidentiality.
5. Framing: Finally, an SSL header is added to the encrypted payload, which is then transmitted to a reliable transport layer protocol.
 Handshake protocol: This protocol is the most complex part of SSL. It allows authentication between the server and the client. It allows the server and the client to negotiate on an encryption and MAC algorithm, and cryptographic keys to be used for encrypting the data in an SSL record. In this protocol, several messages are exchanged between the server and the client. All of these messages have a fixed format with three fields [see Figure 9.17(a)], as listed in the following:
Handshake protocol: This protocol is the most complex part of SSL. It allows authentication between the server and the client. It allows the server and the client to negotiate on an encryption and MAC algorithm, and cryptographic keys to be used for encrypting the data in an SSL record. In this protocol, several messages are exchanged between the server and the client. All of these messages have a fixed format with three fields [see Figure 9.17(a)], as listed in the following:
 Type: This is a 1-byte field indicating one of the ten possible message types. The ten message types are hello_request, client_hello, server_hello, certificate, server_key_exchange, certificate_request, server_done, certificate_verify, client_key_exchange and finished.
Type: This is a 1-byte field indicating one of the ten possible message types. The ten message types are hello_request, client_hello, server_hello, certificate, server_key_exchange, certificate_request, server_done, certificate_verify, client_key_exchange and finished.
 Length: This is a 3-byte field specifying the length of the message in bytes.
Length: This is a 3-byte field specifying the length of the message in bytes.
 Content: This field contains the parameters associated with this message, depending on the message type. For example, in case of hello_request and server_done messages, the parameter list is null. In case of certificate message, the parameter list contains a list of X.509v3 certificates.
Content: This field contains the parameters associated with this message, depending on the message type. For example, in case of hello_request and server_done messages, the parameter list is null. In case of certificate message, the parameter list contains a list of X.509v3 certificates.
The Handshake protocol consists of four phases. These phases are:
1. Establish security capabilities: In this phase, a logical connection is initiated and the security capabilities associated with that connection are established. This is done with the help of two messages, the client_hello and server_hello.
2. Server authentication and key exchange: This phase is initiated by the server. In this phase, the server is authenticated to the client, and the client is made aware of the public key of the server if needed. In this phase, only the server sends the messages, while the client only receives the messages. The messages used in this phase are: certificate, server_key_exchange, certificate_request and server_done.
3. Client authentication and key exchange: This phase is initiated by the client. In this phase, the client is authenticated to the server, and both the client and server know the pre-master secret. In this phase, the client sends the messages, and the server only receives the messages. The messages used in this phase are: certificate, client_key_exchange, certificate_request and certificate_verify.
4. Finish: This is last phase in the SSL handshake protocol, which completes the setting up of a secure connection. It is initiated by the client and terminated by the server. First, two messages, change_cipher_spec and finished, are sent by the client, and then the server responds with two similar messages change_cipher_spec and finished message.
 Change cipher spec protocol: Once the server and the client have negotiated on the cryptographic secrets during the Handshake protocol, the next step is to use these secrets. The change cipher spec is the simplest protocol that is used to signal that the cryptographic secrets are ready for use. This protocol consists of only one message, which consists of a single byte with the value 1 [see Figure 9.17(b)]. This value causes the pending state to be changed to the active state. The pending state is the one in which two communicating parties keep track of the parameters and secrets. The active state is the one in which the two parties use these parameters and secrets to sign/verify or encrypt/decrypt the messages. The change cipher spec protocol is responsible for moving values between the pending state and active state.
Change cipher spec protocol: Once the server and the client have negotiated on the cryptographic secrets during the Handshake protocol, the next step is to use these secrets. The change cipher spec is the simplest protocol that is used to signal that the cryptographic secrets are ready for use. This protocol consists of only one message, which consists of a single byte with the value 1 [see Figure 9.17(b)]. This value causes the pending state to be changed to the active state. The pending state is the one in which two communicating parties keep track of the parameters and secrets. The active state is the one in which the two parties use these parameters and secrets to sign/verify or encrypt/decrypt the messages. The change cipher spec protocol is responsible for moving values between the pending state and active state.
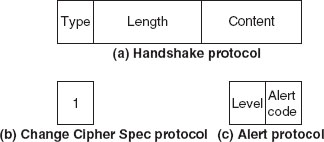
Figure 9.17 Message Format of SSL Protocols
 Alert protocol: This protocol is used to signal errors or any abnormal conditions to the nodes. It enables the nodes to exchange the error or warning information. The type of message associated with alert protocol is the Alert message. There are two bytes in each message of the alert protocol [see Figure 9.17(c)]. The first byte conveys the severity of the error. It can take either the value 1 or 2, where value 1 indicates warning and value 2 indicates fatal. In case of fatal error, the connection is immediately terminated. The second byte contains a code that indicates the specific alert. Some of the possible alert codes are unexpected_message, handshake_failure, decompression_failure, no_certificate, certificate_revoked and certificate_expired.
Alert protocol: This protocol is used to signal errors or any abnormal conditions to the nodes. It enables the nodes to exchange the error or warning information. The type of message associated with alert protocol is the Alert message. There are two bytes in each message of the alert protocol [see Figure 9.17(c)]. The first byte conveys the severity of the error. It can take either the value 1 or 2, where value 1 indicates warning and value 2 indicates fatal. In case of fatal error, the connection is immediately terminated. The second byte contains a code that indicates the specific alert. Some of the possible alert codes are unexpected_message, handshake_failure, decompression_failure, no_certificate, certificate_revoked and certificate_expired.
35. What are the differences between an SSL connection and an SSL session?
Ans.: The differences between an SSL connection and an SSL session are discussed in the following:
A session is established between a client and a server, while a connection is established between two peers having equal roles.
 A session can consist of many connections, while a connection is associated with only one session.
A session can consist of many connections, while a connection is associated with only one session.
 A connection can be terminated and re-established within the same session. When a connection is terminated, the session between the two parties may or may not be terminated. However, when the session is terminated, all the connections of that session also terminate. A session may be suspended or resumed again.
A connection can be terminated and re-established within the same session. When a connection is terminated, the session between the two parties may or may not be terminated. However, when the session is terminated, all the connections of that session also terminate. A session may be suspended or resumed again.
 Data can be exchanged only when the connection between the two parties is established; mere establishment of session is not enough for exchange of data.
Data can be exchanged only when the connection between the two parties is established; mere establishment of session is not enough for exchange of data.
 To create a new session, the communicating parties have to go through a negotiation process. However, to create a new connection within the same session, the negotiation process can be skipped.
To create a new session, the communicating parties have to go through a negotiation process. However, to create a new connection within the same session, the negotiation process can be skipped.
36. Describe briefly the TLS protocol. Also, differentiate between the SSL and TLS protocols.
Ans.: The Transport Layer Security (TLS) protocol is the Internet standard version of the SSL protocol by IETF. Netscape wanted to have a standardized version of SSL, and hence handed over it to IETF. The core idea and implementation of both the protocols are quite similar; however, there are some minor differences. These differences are listed in Table 9.7.
| Property | SSL | TLS |
|---|---|---|
| Version | The commonly used version of SSL is 3.0. | The current version of TLS is 1.0. |
| Cipher suite | An algorithm called Fortezza is used. | The algorithm Fortezza is not used. |
| Cryptography secret | It uses the standard SSL encryption to create a master secret. | A pseudorandom function (PRF) is used to create a master secret. |
| Alert protocol | It uses the standard SSL alert protocol. | The no_certificate alert message is not supported. Some new messages are added, such as decryption_failed, record_overflow, access_denied, unknown_CA, export_restriction, decode_error, protocol_version, insufficient_security and internal_error. |
| Handshake protocol | It uses the standard SSL handshake protocol. | The details of the certificate_verify message and finished message are changed. |
| Record protocol | Uses MAC | Uses HMAC |
37. What is SET? How does SET work? Also, discuss the dual signature for SET and its purpose.
Ans.: The Secure Electronic Transaction (SET) protocol is used for secured credit card transactions over the Internet. SET itself is not a payment system; rather, it contains the security protocols and formats that are used to provide security to the credit card payments made by a user on a public network such as the Internet. The SET concept was started as early as the year 1996, but the first product came to be available only in the year 1998. SET mainly provides three services, which are as follows:
 It provides a secured medium of communication for all the parties involved in a communication.
It provides a secured medium of communication for all the parties involved in a communication.
 It provides trust by the use of X.509v3 digital certificates.
It provides trust by the use of X.509v3 digital certificates.
 It provides complete privacy as the parties involved in the communication can access the information only when and where necessary.
It provides complete privacy as the parties involved in the communication can access the information only when and where necessary.
To understand the working of SET, it is important to know the participants of the SET system. The main participants of SET system are:
 Cardholder: The person who owns the card (such as MasterCard, Visa) and does the purchasing on the Internet.
Cardholder: The person who owns the card (such as MasterCard, Visa) and does the purchasing on the Internet.
 Merchant: The organization or the individual who sells goods or offers services to the cardholder. Usually, these goods and services are offered via a website.
Merchant: The organization or the individual who sells goods or offers services to the cardholder. Usually, these goods and services are offered via a website.
 Issuer: The financial institutions (such as banks) that issue the credit cards and are responsible for the payment of purchases made by the cardholder.
Issuer: The financial institutions (such as banks) that issue the credit cards and are responsible for the payment of purchases made by the cardholder.
 Acquirer: This is also a financial institution that is responsible for establishing an account with the merchant and processing payment card authorizations and payments. Generally, a merchant accepts many credit cards issued by different banks. Since the merchant cannot deal with all the banks, or it cannot have account in all the banks, therefore, it needs an acquirer who provides authorization to the merchant that the card account is valid and active. The acquirer also transfers the payments electronically to the merchant's account. The issuer subsequently reimburses the acquirer over some kind of payment network for electronic funds transfer.
Acquirer: This is also a financial institution that is responsible for establishing an account with the merchant and processing payment card authorizations and payments. Generally, a merchant accepts many credit cards issued by different banks. Since the merchant cannot deal with all the banks, or it cannot have account in all the banks, therefore, it needs an acquirer who provides authorization to the merchant that the card account is valid and active. The acquirer also transfers the payments electronically to the merchant's account. The issuer subsequently reimburses the acquirer over some kind of payment network for electronic funds transfer.
 Acquirer payment gateway: This is an interface between SET and the computer networks of banks for authorization and payment functions.
Acquirer payment gateway: This is an interface between SET and the computer networks of banks for authorization and payment functions.
 Certification authority (CA): This is an organization that offers different classes of certificates for cardholders, merchants and payment gateways.
Certification authority (CA): This is an organization that offers different classes of certificates for cardholders, merchants and payment gateways.
Working of SET
Before using SET, both the cardholder and the merchant must register with the CA. After the registration process, the working of SET involves many steps, which are as follows:
1. The customer browses the merchant's website to evaluate the products offered by the merchant. He or she then selects the products to be purchased and adds them to the shopping cart.
2. The customer then uses a single message to communicate with the merchant and payment gateway. The message has two parts, namely, purchase order, which is used by the merchant, and card information, which is used by the merchant's bank (acquirer).
3. The card information is then forwarded to the acquirer.
4. The acquirer contacts the issuer and checks about payment authorization.
5. If the purchase is authorized, the issuer sends the authorization to the acquirer.
6. A copy of the authorization is also forwarded to the merchant.
7. The merchant completes the order and informs the customer about it.
8. Merchant captures the transaction from its bank.
9. Finally, the credit card invoice is printed by the issuer and provided to the customer.
Dual Signatures
As stated in step 2 of SET, the customer uses a single message to communicate with the merchant and the payment gateway. Therefore, the customer has to ensure that the merchant will not be able to view the payment instruction, and that the acquirer will not be able to view the order instruction. Also, the order and payment has to be linked together, so that the customer can prove that the payment is for the particular order. This whole process is implemented using a concept known as dual signature. The creation of dual signature involves five steps, which are as follows:
1. The customer creates the Payment Information Message Digest (PIMD) by taking the hash (using SHA-1) of the Payment Information (PI).
2. The customer creates another digest, that is, the Order Information Message Digest (OIMD) by taking the hash (again using SHA-1) of the Order Information (OI).
3. Both the PIMD and OIMD are combined together.
4. The combined result is again passed through the hash algorithm SHA-1, and a new digest, Payment Order Message Digest (POMD), is created.
5. Finally, the customer encrypts the POMD with his or her private key using the RSA algorithm, thereby creating the dual signature (DS). This POMD is available to both the merchant and the payment gateway.
Now, the cardholder sends OI, DS and PIMD to the merchant. The merchant verifies that the order information has come from the cardholder, and not from any imposter, by following these steps:
1. The merchant computes its own OIMD by taking hash of OI.
2. The PIMD received from the customer and the computed OIMD are then combined to form a new POMD (say, POMD1).
3. The merchant decrypts the received DS to recover the original POMD.
4. The merchant then compares POMD and POMD1. If both are equal, the message is accepted; otherwise, it is rejected.
Similarly, the payment gateway receives PI, DS and OIMD from the cardholder. Then, it verifies that the payment information has come from the cardholder and not from anyone else. For this, it uses a similar process as used by the merchant to verify the order information. To protect the payment information from the merchant, the cardholder encrypts PI, DS and OIMD with one-time session key K. The key K is also encrypted with the private key of the payment gateway. These two together form a digital envelope, which is sent to the merchant. The merchant is supposed to send this envelope to the payment gateway. Since the merchant does not know the public key of the payment gateway, it cannot decrypt the envelope to obtain the payment details. The payment gateway verifies the authenticity of the cardholder by following these steps.
1. The payment gateway computes its own PIMD by taking hash of PI.
2. The OIMD received from the customer and the computed PIMD are then combined to form a new POMD (say, POMD1).
3. The payment gateway decrypts the received DS to recover the original POMD.
4. The payment gateway then compares the POMD and POMD1. If both are equal, it is verified that the message has come from the cardholder, and not from any imposter.
38. Differentiate between SSL and SET.
Ans.: SSL and SET are both Internet security protocols. However, they differ in some aspects as SET is more secured than SSL. The authentication mechanism used in SET is very complex, which makes it almost impossible for both the sender and receiver to commit any kind of fraud. In a nutshell, SET has been specifically designed for secured e-commerce transactions involving online payments, while SSL has been designed only for exchanging messages over the Internet. The main differences between SSL and SET are listed in the Table 9.8.
| Issue | SSL | SET |
|---|---|---|
| Main objective | To allow exchange of data in an encrypted form | To support e-commerce-related payment mechanisms |
| Certification | The certificates are exchanged between the two parties. | A trusted third party certifies all the parties involved in the communication process. |
| Authentication | The authentication mechanism is not very strong. | The authentication mechanism is very strong. |
| Risk of merchant fraud | It is prone to merchant fraud as financial data is provided to the merchant. | It is free from this fraud as financial data is given to the payment gateway only. |
| Risk of customer fraud | It is prone to this kind of fraud as the customer can refuse to pay later; there is no mechanism that can prevent such kind of fraud. | The payment instructions are digitally signed by the customer. Thus, there is less chance of such fraud. |
| Action in case of customer fraud | Merchant is responsible if a customer later refuses to pay | Payment gateway is responsible in case of customer fraud. |
| Practical usage | High | Less |
Multiple-choice Questions
1. Which server acts as KDC in the Kerberos protocol?
(a) TGS
(b) AS
(c) Real server
(d) None of these
2. Which encryption algorithm is used in the Kerberos 4 protocol?
(a) AES
(b) Block cipher
(c) DES
(d) Triple DES
3. In which year was X.509 first issued?
(a) 1988
(b) 1978
(c) 1982
(d) 1994
4. Who issues the PGP certificates?
(a) ITU-T
(b) IEEE
(c) IETF
(d) The users themselves
5. What are the two modes that IPSec protocol works on?
(a) On and Off
(b) Transport and Tunnel
(c) Forward and Backward
(d) Linked and Unlinked
6. Which of the following are IPSec protocols?
(a) PGP and S/MIME
(b) Kerberos 4, Kerberos 5
(c) AH and ESP
(d) SSL and SET
7. Which algorithm solves the man-in-the-middle attack problem?
(a) Diffie-Hellman
(b) RSA
(c) Oakley
(d) ISAKMP
8. Which of the following Internet security protocols is used for secure credit card payments?
(a) SET
(b) PGP
(c) SSL
(d) TLS
9. The _________ protocol uses the Fortezza algorithm.
(a) TLS
(b) SET
(c) ESP
(d) SSL
10. In which protocol is the payment gateway used?
(a) SET
(b) PGP
(c) TLS
(d) SSL
Answers
1. (b)
2. (c)
3. (a)
4. (d)
5. (b)
6. (c)
7. (c)
8. (a)
9. (d)
10.(a)
1. What do you mean by the term intruders? Explain intrusion techniques in brief.
Ans.: Intruders are the attackers who attempt to breach the security of a network. They attack the network in order to get unauthorized access. Intruders are of three types, namely, masquerader, misfeasor and clandestine user.
 Masquerader is an external user who is not authorized to use a computer, and yet tries to gain privileges to access a legitimate user's account. Masquerading is generally done either using stolen IDs and passwords, or through bypassing authentication mechanisms.
Masquerader is an external user who is not authorized to use a computer, and yet tries to gain privileges to access a legitimate user's account. Masquerading is generally done either using stolen IDs and passwords, or through bypassing authentication mechanisms.
 Misfeasor is a legitimate user who either accesses some applications or data without sufficient privileges to access them, or has privilege to access them, but misuses these privileges. A misfeasor is generally an internal user.
Misfeasor is a legitimate user who either accesses some applications or data without sufficient privileges to access them, or has privilege to access them, but misuses these privileges. A misfeasor is generally an internal user.
 Clandestine user is either an internal or external user who gains administrative control of the system and tries to avoid access control and auditing information.
Clandestine user is either an internal or external user who gains administrative control of the system and tries to avoid access control and auditing information.
Intrusion Techniques
The intruders always indulge in finding some way to gain access to the system or to increase the number of privileges assigned to them. To do this, the intruders need access to information that should have been protected, such as some legitimate user's password. After learning the password of an authorized user, intruders can use it to log on to the system and misuse the privileges assigned to the authorized user. Some techniques that the intruders can use to learn others' passwords are as listed here:
 They can try the passwords that are by default assigned to standard accounts such as administrator, as it is possible that the administrators may not change their passwords.
They can try the passwords that are by default assigned to standard accounts such as administrator, as it is possible that the administrators may not change their passwords.
 They can thoroughly test all the short passwords made up of one, two or three characters.
They can thoroughly test all the short passwords made up of one, two or three characters.
 They can intercept the communication between the host system and a remote user.
They can intercept the communication between the host system and a remote user.
 They can use a malicious program, such as a Trojan horse, to get around the restrictions imposed on access.
They can use a malicious program, such as a Trojan horse, to get around the restrictions imposed on access.
 They can try the words that are available in the system's online dictionary or that are expected to be used.
They can try the words that are available in the system's online dictionary or that are expected to be used.
 They can try the users' personal information such as their IDs, phone numbers, room numbers, names of their spouses and children, birthdates, etc.
They can try the users' personal information such as their IDs, phone numbers, room numbers, names of their spouses and children, birthdates, etc.
Besides learning passwords, the intruders can go for other ways to gain access to the system or to gain further privileges. For example, they can exploit attacks such as buffer overflows on a program that executes with certain privileges.
2. Discuss password protection approaches.
Ans.: Generally, passwords are stored by the system in a password file along with the user IDs. Thus, to protect passwords from being captured by the intruders, it is necessary to protect the password file. There are two ways to protect the password file, as listed here:
 One-way function: The system does not store the passwords in a clear form in the password file; rather, it applies a function on the user's password and stores the resulting value in the password file. Whenever a user attempts to log on to the system with the help of his or her user ID and password, the system applies the same function on the supplied password. Then it checks whether the newly computed value matches with the stored value. If so, the user is authenticated and allowed access; otherwise, access is denied. The advantage of using this method of protecting the password file is that even if an intruder gets access to the password file, he or she will not be able to get the passwords.
One-way function: The system does not store the passwords in a clear form in the password file; rather, it applies a function on the user's password and stores the resulting value in the password file. Whenever a user attempts to log on to the system with the help of his or her user ID and password, the system applies the same function on the supplied password. Then it checks whether the newly computed value matches with the stored value. If so, the user is authenticated and allowed access; otherwise, access is denied. The advantage of using this method of protecting the password file is that even if an intruder gets access to the password file, he or she will not be able to get the passwords.
 Access control: Another means of protecting the password file is by restricting access to the password file. Only a few users such as the system administrator must be allowed to access the password file.
Access control: Another means of protecting the password file is by restricting access to the password file. Only a few users such as the system administrator must be allowed to access the password file.
3. Explain any two approaches for intrusion detection.
Ans.: To prevent intruders from getting unauthorized access to the system, intrusion prevention and intrusion detection can be used. Intrusion prevention is a process that involves detecting the signs of intrusion and attempting to stop the intrusion efforts. On the other hand, intrusion detection is a process that involves monitoring the actions occurring on the network or in the computer systems. In intrusion detection, analysis is done to detect the sign of violations of computer security policies, standard security policies or acceptable use of policies.
It is not possible to completely prevent the efforts of intruders as they constantly try to find their way into the secured system. Hence, we mainly focus on intrusion detection, as it helps collect more information about intrusions. There are generally two approaches for intrusion detection, as listed here:
 Statistical anomaly detection: In this category, the behaviour of legitimate users is evaluated over some time interval. That is, their actions are captured as statistical data and then, by applying certain rules on the collected data, their behaviour is checked to determine the legitimacy of the users. This can be achieved by two ways, namely, threshold detection and profile-based detection.
Statistical anomaly detection: In this category, the behaviour of legitimate users is evaluated over some time interval. That is, their actions are captured as statistical data and then, by applying certain rules on the collected data, their behaviour is checked to determine the legitimacy of the users. This can be achieved by two ways, namely, threshold detection and profile-based detection.
 Threshold detection: In threshold detection, thresholds are defined for all users as a group, and the total number of events that are attributed to the user are measured against these threshold values. The number of events is assumed to round up to a number that is most likely to occur, and if the event count exceeds this number, then intrusion is said to have occurred.
Threshold detection: In threshold detection, thresholds are defined for all users as a group, and the total number of events that are attributed to the user are measured against these threshold values. The number of events is assumed to round up to a number that is most likely to occur, and if the event count exceeds this number, then intrusion is said to have occurred.
 Profile-based detection: In profile-based detection, profiles for all users are created, and then matched with available statistical data to find out if any unwanted action has been performed. A user profile contains several parameters; therefore, change in a single parameter is not a sign of alert.
Profile-based detection: In profile-based detection, profiles for all users are created, and then matched with available statistical data to find out if any unwanted action has been performed. A user profile contains several parameters; therefore, change in a single parameter is not a sign of alert.
 Rule-based detection: In this category, certain rules are applied on the actions performed by the users. These rules can determine whether an action performed by any user is suspicious enough to be classified as an intrusion attempt. Rule-based detection is classified into two types, namely, anomaly detection and penetration identification.
Rule-based detection: In this category, certain rules are applied on the actions performed by the users. These rules can determine whether an action performed by any user is suspicious enough to be classified as an intrusion attempt. Rule-based detection is classified into two types, namely, anomaly detection and penetration identification.
 Anomaly-based detection: In anomaly-based detection, the usage patterns of users are collected, and certain rules are applied to check any deviation from the previous usage pasterns. The collected patterns are defined by the set of rules that includes past behaviour patterns of users, programs, privileges, time-slots, terminals, etc. The current behaviour patterns of the user are matched with the defined set of rules to check whether there is any deviation in the patterns. In this approach, a large database of rules is needed.
Anomaly-based detection: In anomaly-based detection, the usage patterns of users are collected, and certain rules are applied to check any deviation from the previous usage pasterns. The collected patterns are defined by the set of rules that includes past behaviour patterns of users, programs, privileges, time-slots, terminals, etc. The current behaviour patterns of the user are matched with the defined set of rules to check whether there is any deviation in the patterns. In this approach, a large database of rules is needed.
 Penetration identification: In penetration identification, an expert system is maintained that looks for any unwanted attempts. This system also contains rules that are used to identify the suspicious behaviour and penetrations that can exploit known weaknesses. Here, the rules are generated by interviewing experts such as system administrators and security analysts. The data collected in the interview process consist of known penetration scenarios and events that may threaten the security of the system. Thus, the rules are confined to the system and the operating system that is being used.
Penetration identification: In penetration identification, an expert system is maintained that looks for any unwanted attempts. This system also contains rules that are used to identify the suspicious behaviour and penetrations that can exploit known weaknesses. Here, the rules are generated by interviewing experts such as system administrators and security analysts. The data collected in the interview process consist of known penetration scenarios and events that may threaten the security of the system. Thus, the rules are confined to the system and the operating system that is being used.
4. Explain audit records.
Ans.: An audit record (also known as audit log) is a very important tool used in intrusion detection. Audit records are used to track the actions performed by users. If any user tries to get unauthorized access in a network, then traces of such actions can be detected in these records, so that appropriate measures can be taken. Audit records can be categorized into two types, namely, native auditrecords and detection-specific audit records.
 Native audit records: Almost all multiuser operating systems come with in-built accounting software that collects information about the actions of each user. The advantage of using this approach is that there is no need for additional collection software. However, the disadvantage is that some of the needed information may not be available in the native audit record or may be in a form that is not convenient to use.
Native audit records: Almost all multiuser operating systems come with in-built accounting software that collects information about the actions of each user. The advantage of using this approach is that there is no need for additional collection software. However, the disadvantage is that some of the needed information may not be available in the native audit record or may be in a form that is not convenient to use.
 Detection-specific audit records: These records record only specific information that is related to the detection of unauthorized access in a network. These types of records contain more focused information, but duplication of information may happen. The advantage of using this approach is that it could be made vendor-independent and can be ported onto different systems. However, the disadvantage of this approach is the extra overhead, as two accounting packages need to remain on a single machine.
Detection-specific audit records: These records record only specific information that is related to the detection of unauthorized access in a network. These types of records contain more focused information, but duplication of information may happen. The advantage of using this approach is that it could be made vendor-independent and can be ported onto different systems. However, the disadvantage of this approach is the extra overhead, as two accounting packages need to remain on a single machine.
Irrespective of the type, each audit record contains some fields, as listed here:
 Subject: This field gives the information of the user or process or terminal who has started an action.
Subject: This field gives the information of the user or process or terminal who has started an action.
 Action: This field defines the operation performed by the user (subject) on an object. For example, read/write, login, execute, print, I/O activity, etc.
Action: This field defines the operation performed by the user (subject) on an object. For example, read/write, login, execute, print, I/O activity, etc.
 Object: This field provides the information of the receiver who has received the action. For example, database record, a disk file or an application program.
Object: This field provides the information of the receiver who has received the action. For example, database record, a disk file or an application program.
 Exception-condition: This field stores the result of any exception condition, if any occurs because of the actions performed by the subject on the object.
Exception-condition: This field stores the result of any exception condition, if any occurs because of the actions performed by the subject on the object.
 Resource-usage: This field records the information regarding the usage of resources in performing an action. For example, the disk space, or CPU time used by an action, number of lines printed or displayed, or number of I/O units used.
Resource-usage: This field records the information regarding the usage of resources in performing an action. For example, the disk space, or CPU time used by an action, number of lines printed or displayed, or number of I/O units used.
 Time-stamp: This field indicates the unique date and time stamp that indicates when an action was executed.
Time-stamp: This field indicates the unique date and time stamp that indicates when an action was executed.
5. Why is distributed intrusion detection needed? Explain its architecture.
Ans.: A typical organization consists of a large collection of hosts distributed over a LAN or supported by an internetwork. One way to detect intrusion in such an organization is to use stand-alone intrusion detection systems on individual hosts. Though this type of defence is possible, it has not proved to be much effective. Thus, a better and more effective defence is required, which is achieved through coordination and cooperation among the intrusion detection systems across the network.
Figure 10.1 shows the architecture of a distributed intrusion detection system that was developed at the University of California. It consists of the following three components:
 Host agent module: This is an audit collection module that runs as a background process on the system being monitored. It is responsible for collecting information related to security on the host and reporting this to the central manager.
Host agent module: This is an audit collection module that runs as a background process on the system being monitored. It is responsible for collecting information related to security on the host and reporting this to the central manager.
 LAN manager agent module: This module works in a similar manner as that of a host agent module. However, the difference is that it examines the LAN traffic, as its name implies, rather than security-related events. It also reports the results of analysis to the central manager.
LAN manager agent module: This module works in a similar manner as that of a host agent module. However, the difference is that it examines the LAN traffic, as its name implies, rather than security-related events. It also reports the results of analysis to the central manager.
 Central manager module: This is the main module that is responsible for processing and correlating the reports received from the host agent module and LAN manager agent module in order to detect the intrusion.
Central manager module: This is the main module that is responsible for processing and correlating the reports received from the host agent module and LAN manager agent module in order to detect the intrusion.
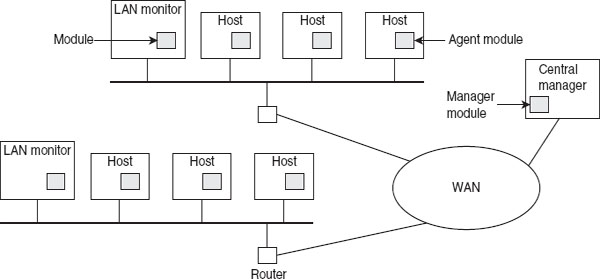
Figure 10.1 Architecture of Distributed Intrusion Detection System
6. List some issues in the design of distributed intrusion detection systems.
Ans.: Although distributed intrusion detection systems are an effective way to prevent intrusion across the network, there are still some issues in its design. These issues are discussed as follows:
 In case different hosts in a network are not similar (that is, heterogeneous environment), the native audit collection system used by each host may differ. Further, if intrusion detection is used, different hosts may have their own format for security-related audit records. This necessitates a distributed intrusion detection system to deal with different audit formats.
In case different hosts in a network are not similar (that is, heterogeneous environment), the native audit collection system used by each host may differ. Further, if intrusion detection is used, different hosts may have their own format for security-related audit records. This necessitates a distributed intrusion detection system to deal with different audit formats.
 The intrusion detection system can be implemented using either centralized or decentralized architecture. If centralized architecture is used, the entire audit data is collected and analyzed at
a single central location. Though centralizing the data makes the task of correlating the reports easier, it results in a serious bottleneck in case of failure of the central location. On the other hand, if decentralized architecture is used, we have more than one location to collect and analyze the data. To work effectively, the coordination and exchange of information among these locations is required, which results in an extra overhead. Therefore, the choice of which architecture is to be employed is a matter of concern.
The intrusion detection system can be implemented using either centralized or decentralized architecture. If centralized architecture is used, the entire audit data is collected and analyzed at
a single central location. Though centralizing the data makes the task of correlating the reports easier, it results in a serious bottleneck in case of failure of the central location. On the other hand, if decentralized architecture is used, we have more than one location to collect and analyze the data. To work effectively, the coordination and exchange of information among these locations is required, which results in an extra overhead. Therefore, the choice of which architecture is to be employed is a matter of concern.
 As many nodes in the network are responsible for collecting and analyzing the audit data, either the raw audit data or summary data needs to be transmitted across the network. This necessitates ensuring the integrity and confidentiality of data being transmitted. Integrity refers to ensuring that the data is not altered by the intruder, and confidentiality is about maintaining the secrecy of the data.
As many nodes in the network are responsible for collecting and analyzing the audit data, either the raw audit data or summary data needs to be transmitted across the network. This necessitates ensuring the integrity and confidentiality of data being transmitted. Integrity refers to ensuring that the data is not altered by the intruder, and confidentiality is about maintaining the secrecy of the data.
7. What are honeypots?
Ans.: Honeypots are a recent innovation in intrusion detection technology. They are the traps that are designed to attract the potential intruders and, thus, track their activities. The main aim of such systems is to collect the information about the intruder's activities, deviate them from accessing the critical systems and boost them to stay on the system for more time so that the network administrator can take actions accordingly.
Honeypots are fabricated to look like real systems by putting real-looking information into them, so that they appear valuable to the potential intruders. However, legitimate users are not allowed to know about or access these systems. Thus, if anyone accesses the honeypots, he or she is a potential attacker. Honeypots are equipped with sensors and loggers to detect accesses and to track the intruder's activities.
8. How are passwords stored in a password file in the UNIX operating system? How are users authenticated?
Ans.: Earlier, in the UNIX operating system, passwords of all users were stored in plaintext in the password file, and the password file was protected by allowing it to be accessed only by the system administrator and privileged users. However, this practice may prove dangerous because any mistake in programming or any other error can make the password file vulnerable to attack. Thus, a new scheme is now used in the UNIX operating system, where the passwords are not stored in plaintext in the password file; instead, a hash of the password is computed and stored in the password file.
Each user in UNIX is allowed to choose a password of maximum eight printable characters, which are converted using 7-bit ASCII to form a 56-bit value. This 56-bit value is used as the encryption key in the encryption function, crypt(3). The crypt(3) function is based on the Data Encryption Standard (DES) algorithm. In UNIX, DES algorithm is modified with the help of 12-bit salt—a value indicating the time a password was assigned to a user. To store a password in the password file, the modified DES algorithm takes a 64-bit block consisting of 0s and encrypts it using the 56-bit encryption key. The resulting 64-bit ciphertext block serves as input for the next encryption. A total of 25 encryptions are performed, and the final obtained 64-bit ciphertext is converted to 11 printable characters. This hashed password is then stored in the password file along with the user ID and the salt.
At the time a user attempts to log on to the system, he or she presents his or her user ID and password to the system. The UNIX operating system uses the supplied user ID as index to find the corresponding entry in the password file. After finding the entry, it extracts the plaintext salt and hashed
password. The salt along with the password supplied by the user are given as input to the crypt(3) function, which then repeats the same process as described earlier to compute the hash of the password. If the newly computed value matches with the stored value in the password file, the user is authenticated; otherwise, the access is denied.
9. Discuss some password selection strategies.
Ans.: Generally, users choose passwords that are short and easy to remember. However, such passwords may be easily guessed, making it simple for intruders to hack into the corresponding user's accounts. On the other hand, if passwords given to the users are long and are randomly generated, it is not effectively possible to crack the passwords. However, such passwords are hard to remember for the users. Thus, some password-selection strategies have been introduced with the aim of building a password that cannot be easily guessed and can be easily remembered. These strategies are listed here:
 User education: This strategy is based on educating the users about the importance of using strong passwords that are difficult to guess. The users can also be provided with certain guidelines that help them in choosing hard-to-guess passwords. Though this strategy is simple, it generally fails, especially when there are a large number of users. This is because many users simply ignore the guidelines of selecting strong passwords, while others are unable to judge what a strong password is.
User education: This strategy is based on educating the users about the importance of using strong passwords that are difficult to guess. The users can also be provided with certain guidelines that help them in choosing hard-to-guess passwords. Though this strategy is simple, it generally fails, especially when there are a large number of users. This is because many users simply ignore the guidelines of selecting strong passwords, while others are unable to judge what a strong password is.
 Computer-generated passwords: In this strategy, the system randomly generates passwords for the users. Being random, these passwords may or may not be correctly pronounceable. Thus, it becomes difficult for the users to remember the passwords. The situation becomes even worse in case the password is not pronounceable because, in that case, the user does not have any choice except to write down the password somewhere, which makes it subject to be stolen by an intruder. Therefore, this technique is not so popular among the users.
Computer-generated passwords: In this strategy, the system randomly generates passwords for the users. Being random, these passwords may or may not be correctly pronounceable. Thus, it becomes difficult for the users to remember the passwords. The situation becomes even worse in case the password is not pronounceable because, in that case, the user does not have any choice except to write down the password somewhere, which makes it subject to be stolen by an intruder. Therefore, this technique is not so popular among the users.
 Reactive password checking: In this strategy, the system executes its own password cracker at regular intervals of time to identify passwords that can be guessed easily. The idea is to determine easy-to-guess passwords and to reject them, thus, improving password security. The system also notifies the corresponding users about the cancellation of their passwords. The disadvantage of this strategy is that any easy-to-guess password in the system remains vulnerable to attack as long as it is not found by the password cracker of the system.
Reactive password checking: In this strategy, the system executes its own password cracker at regular intervals of time to identify passwords that can be guessed easily. The idea is to determine easy-to-guess passwords and to reject them, thus, improving password security. The system also notifies the corresponding users about the cancellation of their passwords. The disadvantage of this strategy is that any easy-to-guess password in the system remains vulnerable to attack as long as it is not found by the password cracker of the system.
 Proactive password checker: This strategy allows users to select their passwords on their own. However, it provides sufficient guidance to the users at the time of password selection so that they can select passwords that are strong as well as easy to remember. To achieve this, the system may employ certain rules that must be followed by each user while selecting the password. For example, the system may enforce a rule that the password must be minimum eight characters long and must be the combination of lower case letters, upper case letters and numeric digits. Now, at the time of password selection, if all rules are followed by the user, the system allows the password, else rejects it.
Proactive password checker: This strategy allows users to select their passwords on their own. However, it provides sufficient guidance to the users at the time of password selection so that they can select passwords that are strong as well as easy to remember. To achieve this, the system may employ certain rules that must be followed by each user while selecting the password. For example, the system may enforce a rule that the password must be minimum eight characters long and must be the combination of lower case letters, upper case letters and numeric digits. Now, at the time of password selection, if all rules are followed by the user, the system allows the password, else rejects it.
The proactive password checker strategy is based on creating a balance between the strength of the password and user acceptability. This is essential because, if the system chooses a complex algorithm for determining whether a selected password is acceptable, then too many password rejections may occur and, as a result, the user may not find the system user-friendly. In contrast, if the system uses a simple algorithm, then it may enable a password cracker to understand the basis of password selection and, thus, help them to guess the passwords easily.
10. What do you understand by malicious software?
Ans.: Malicious software (shortened form malware) are programs that generate threats to the computer system and stored data. They could be in the form of viruses, worms, Trojan horses, logic bombs and zombie programs. All malicious programs fall under two categories: one that require a host program such as an application program or a system program in order to be executed by the operating system, and another that can be executed by the operating system independently. Some examples of malicious programs belonging to first category include viruses and logic bombs, while worms and zombie programs are examples of the second category.
11. What is a virus? Explain different types of viruses.
Ans.: Virus (stands for Vital Information Resources Under Seize) is a program or small code segment that is designed to replicate, attach to other programs and perform unsolicited and malicious actions. It enters into the computer system from external sources such as CD, pen drive or e-mail and executes when the infected program is executed. Further, as an infected computer gets in contact with an uninfected computer (for example, through computer networks), the virus may pass on to the uninfected system and destroy data.
Just as flowers are attractive to the bees that pollinate them, virus host programs are deliberately made attractive to victimize the user. They become destructive as soon as they enter a system or are programmed to lie dormant until activated by a trigger. The different types of virus are discussed as follows:
 Boot sector virus: This virus infects the master boot record of a computer system. This virus moves the boot record to another sector on the disk, or replaces it with the infected one. It then marks that sector as a bad sector on the disk. This type of virus is very difficult to detect since the boot sector is the first program that is loaded when a computer starts. In effect, the boot sector virus takes full control of the infected computer.
Boot sector virus: This virus infects the master boot record of a computer system. This virus moves the boot record to another sector on the disk, or replaces it with the infected one. It then marks that sector as a bad sector on the disk. This type of virus is very difficult to detect since the boot sector is the first program that is loaded when a computer starts. In effect, the boot sector virus takes full control of the infected computer.
 File-infecting virus: This virus infects files with the extensions .com and .exe. This type of virus usually resides inside the memory and infects most of the executable files on a system. The virus replicates by attaching a copy of itself to an uninfected executable program. It then modifies the host programs and, subsequently, when the program is executed, it executes along with it. File-infecting virus can only gain control of the computer if the user or the operating system executes a file infected with the virus.
File-infecting virus: This virus infects files with the extensions .com and .exe. This type of virus usually resides inside the memory and infects most of the executable files on a system. The virus replicates by attaching a copy of itself to an uninfected executable program. It then modifies the host programs and, subsequently, when the program is executed, it executes along with it. File-infecting virus can only gain control of the computer if the user or the operating system executes a file infected with the virus.
 Polymorphic virus: This virus changes its code as it propagates from one file to another. Therefore, each copy of virus appears different from others; however, they are functionally similar. This makes the polymorphic virus difficult to detect, like the stealth virus. The variation in copies is achieved by placing superfluous instructions in the virus code or by interchanging the order of instructions that are not dependent. Another more effective means to achieve variation is by using encryption. A part of the virus, called the mutation engine, generates a random key that is used to encrypt the rest of the virus. The random key is kept stored with the virus, while the mutation engine changes by itself. At the time the infected program is executed, the stored key is used by the virus to decrypt itself. Each time the virus replicates, the random key changes.
Polymorphic virus: This virus changes its code as it propagates from one file to another. Therefore, each copy of virus appears different from others; however, they are functionally similar. This makes the polymorphic virus difficult to detect, like the stealth virus. The variation in copies is achieved by placing superfluous instructions in the virus code or by interchanging the order of instructions that are not dependent. Another more effective means to achieve variation is by using encryption. A part of the virus, called the mutation engine, generates a random key that is used to encrypt the rest of the virus. The random key is kept stored with the virus, while the mutation engine changes by itself. At the time the infected program is executed, the stored key is used by the virus to decrypt itself. Each time the virus replicates, the random key changes.
 Stealth virus: This virus attempts to conceal its presence from the user. It makes use of compression such that the length of infected program is exactly same as that of the uninfected version. For example, it may keep intercept logic in some I/O routines so that when some other program requests for information from the suspicious portions of the disk using these routines, it will present the original uninfected version to the program. The Stoned Monkey virus is an example
of stealth virus. This virus uses ‘read stealth’ capability, and if a user executes a disk-editing or antivirus program to examine the main boot record, the user would not find any evidence of infection.
Stealth virus: This virus attempts to conceal its presence from the user. It makes use of compression such that the length of infected program is exactly same as that of the uninfected version. For example, it may keep intercept logic in some I/O routines so that when some other program requests for information from the suspicious portions of the disk using these routines, it will present the original uninfected version to the program. The Stoned Monkey virus is an example
of stealth virus. This virus uses ‘read stealth’ capability, and if a user executes a disk-editing or antivirus program to examine the main boot record, the user would not find any evidence of infection.
 Multipartite virus: This virus infects both boot sectors and executable files, and uses both mechanisms to spread. It is the worst virus of all because it can combine some or all of the stealth techniques along with polymorphism to prevent detection. For example, if a user runs an application infected with a multipartite virus, the virus activates and infects the hard disk's master boot record. Moreover, the next time the computer starts; the virus gets activated again and starts infecting every program that the user runs. One-half virus is an example of a multipartite virus, which exhibits both stealth and polymorphic behaviour.
Multipartite virus: This virus infects both boot sectors and executable files, and uses both mechanisms to spread. It is the worst virus of all because it can combine some or all of the stealth techniques along with polymorphism to prevent detection. For example, if a user runs an application infected with a multipartite virus, the virus activates and infects the hard disk's master boot record. Moreover, the next time the computer starts; the virus gets activated again and starts infecting every program that the user runs. One-half virus is an example of a multipartite virus, which exhibits both stealth and polymorphic behaviour.
12. What are the typical phases of operation of a virus?
Ans.: Virus is a destructive program that attaches to other programs, replicates itself and performs malicious actions when the host program is executed. The whole operation of a virus involves the following four phases.
 Dormant phase: This is the initial phase in the lifetime of a virus. During this phase, the virus remains idle; however, later, it is activated due to occurrence of some events including the date, time, capacity of disk beyond limit or the presence of some other program or file. It may be noted that this phase exists only in case of some viruses and not all.
Dormant phase: This is the initial phase in the lifetime of a virus. During this phase, the virus remains idle; however, later, it is activated due to occurrence of some events including the date, time, capacity of disk beyond limit or the presence of some other program or file. It may be noted that this phase exists only in case of some viruses and not all.
 Propagation phase: During this phase, the virus replicates itself and infects other programs as well as some disk areas by putting its identical copies (referred to as clones) into them. All the infected programs now contain the same virus, which has already entered into the propagation phase.
Propagation phase: During this phase, the virus replicates itself and infects other programs as well as some disk areas by putting its identical copies (referred to as clones) into them. All the infected programs now contain the same virus, which has already entered into the propagation phase.
 Triggering phase: In this phase, the virus is activated to enter the execution phase, so that it can perform its intended action. The activation of the virus may occur due to the events as specified in dormant phase. In addition, it also takes into account the number of times a single copy of virus replicates itself.
Triggering phase: In this phase, the virus is activated to enter the execution phase, so that it can perform its intended action. The activation of the virus may occur due to the events as specified in dormant phase. In addition, it also takes into account the number of times a single copy of virus replicates itself.
 Execution phase: This is the last phase of the virus's operation where it performs the function for which it was designed. The functions performed by viruses range from simple harmless functions such as displaying a message on the screen to serious malicious functions such as destroying programs and data files.
Execution phase: This is the last phase of the virus's operation where it performs the function for which it was designed. The functions performed by viruses range from simple harmless functions such as displaying a message on the screen to serious malicious functions such as destroying programs and data files.
13. Write a short note on the following:
(a) Worms
(b) Trojan horses
(c) Logic bomb
(d) Spyware
Ans.: (a) Worms: Worms are programs constructed to infiltrate into legitimate data processing programs and alter or destroy the data. They often use network connections to spread from one computer system to another; thus, worms attack systems that are linked through communication lines. Once active within a system, worms behave like a virus and perform a number of disruptive actions. To reproduce themselves, worms make use of network medium such as: network mail facility, in which a worm can mail a copy of itself to other systems, remote execution capability, in which a worm can execute a copy of itself on another system and remote log in capability, whereby a worm can log into a remote system as a user and then use commands to copy itself from one system to another.
Both worms and viruses tend to fill computer memory with useless data thereby preventing users from using memory space for the intended applications or programs. In addition, they can destroy or modify data and programs to produce erroneous results, as well as halt the operation of a computer
system or network. Similar to a virus, the operation of a network worm also involves dormant, propagation, triggering and execution phases.
(b)Trojan horse: A Trojan horse is a malicious program that appears to be legal and useful but concurrently does something unexpected, such as destroying existing programs and files. It does not replicate itself in the computer system and, hence, it is not a virus. However, it usually opens the way for other malicious programs such as viruses to enter into the computer system. In addition, it may also allow unauthorized users to access the information stored in the computer.
Trojan horses spread when users are convinced to open or download a program because they think it has come from a legitimate source. They can also be included in software that is freely downloadable. They are usually subtler, especially in the cases where they are used for espionage. They can be programmed to self-destruct, without leaving any evidence other than the damage they have caused. The most famous Trojan horse is a program called back orifice, which is an unsubtle play of words on Microsoft's Back Office suite of programs for NT server. This program allows anybody to have the complete control over the computer or server it occupies.
(c)Logic bomb: A logic bomb is a program or portion of a program that lies dormant until a specific part of program logic is activated. The most common activator for a logic bomb is date. The logic bomb periodically checks the computer system date and does nothing until a pre-programmed date and time is reached. It could also be programmed to wait for a certain message from the programmer. When logic bomb sees the message, it gets activated and executes the code. A logic bomb can also be programmed to activate on a wide variety of other variables such as when a database grows past a certain size or a user's home directory is deleted. For example, the well-known logic bomb is a Michelangelo, which has a trigger set for Michelangelo's birthday. On the given birth date, it causes system crash or data loss or other unexpected interactions with existing code.
(d)Spyware: Spyware are the small programs that install themselves on computers to gather data secretly about the computer user without his or her consent and report the collected data to interested users or parties. The information gathered by the spyware may include e-mail addresses and passwords, net surfing activities, credit card information, etc. Spyware often gets automatically installed on your computer when you download a program from the Internet or click any option from pop-up windows in the browser.
14. What is an antivirus? What are its approaches?
Ans.: An antivirus is an application software that is used for providing protection against malicious software. It is a software utility that (upon installing on a computer) detects viruses and, if found, tries to remove them. The built-in scanner of antivirus software scans all the files on the computer's hard disk to look for particular types of code within programs. Most antivirus programs include an auto-update feature that enables the program to download profiles of new viruses so that it can check for the new viruses as soon as they are discovered. The most popular available antivirus software includes Norton antivirus, McAfee antivirus and Quick Heal antivirus.
Antivirus Approaches
A simple and ideal approach against threat of viruses is to prevent them from entering into the system. Practically, it is not possible to achieve total prevention; however, the frequency of successful virus attacks can be reduced. Thus, an alternative approach is used that is based on the detection, identification and removal of viruses from the infected programs.
 Detection: In case the system has been infected by viruses, the first step is to identify that the infection has occurred and where it has occurred, that is, the location of the virus.
Detection: In case the system has been infected by viruses, the first step is to identify that the infection has occurred and where it has occurred, that is, the location of the virus.
 Identification: After the infection has been detected and the virus located, the next step is to determine the specific type of virus that has infected the file.
Identification: After the infection has been detected and the virus located, the next step is to determine the specific type of virus that has infected the file.
 Removal: After identifying the specific virus in a file, the final step is to remove it completely from the infected file and to bring the file back to its original state. The virus must be removed from all the systems in the network in order to prevent it from spreading further.
Removal: After identifying the specific virus in a file, the final step is to remove it completely from the infected file and to bring the file back to its original state. The virus must be removed from all the systems in the network in order to prevent it from spreading further.
15. List and brief the different generations of antivirus software.
Ans.: Earlier, viruses were simple code fragments; thus, antivirus software packages used for those viruses were also simpler. However, with the evolution in virus as well as antivirus technology, the attackers have generated more complex viruses that are not easily detectable. To protect against such viruses, antivirus software have also grown complex. The growth of antivirus software has been divided into four generations which are as follows:
 First generation: The antivirus software of this generation used simple scanners that rely on virus signatures to detect viruses. It detects viruses that have basically the same structure and the same bit pattern in all copies. However, these types of scanners can detect only the known viruses. Another type of scanner used in the first generation maintains a record of the program length, and monitors the change in length for detecting the viruses.
First generation: The antivirus software of this generation used simple scanners that rely on virus signatures to detect viruses. It detects viruses that have basically the same structure and the same bit pattern in all copies. However, these types of scanners can detect only the known viruses. Another type of scanner used in the first generation maintains a record of the program length, and monitors the change in length for detecting the viruses.
 Second generation: The antivirus software of this generation used heuristic scanners that rely on some heuristic rules to detect virus infections. One approach to detect virus infection is to scan the files and look for code fragments that are usually related to viruses. For example, in case of a polymorphic virus, the scanner may determine the starting of the encryption loop and then find the encryption key. Once the scanner has found the key, it cleans the virus infection from the infected program by decrypting the code fragment with the key and then returns the virus-free program back to service.
Second generation: The antivirus software of this generation used heuristic scanners that rely on some heuristic rules to detect virus infections. One approach to detect virus infection is to scan the files and look for code fragments that are usually related to viruses. For example, in case of a polymorphic virus, the scanner may determine the starting of the encryption loop and then find the encryption key. Once the scanner has found the key, it cleans the virus infection from the infected program by decrypting the code fragment with the key and then returns the virus-free program back to service.
Another approach for detecting virus infection is integrity checking. In this approach, a checksum is added at the end of each program. If any program gets infected by a virus, however, with no change in the checksum, the change in program can be detected by performing an integrity check. On the other hand, if a virus is so complex that it changes the checksum in addition to the program, then an encrypted hash function can be used to deal with the virus. By storing the encryption key at a different location from that of the program, we can prevent a virus from generating a new hash code and then encrypting it. Moreover, the use of the hash function instead of checksum prevents the virus from adapting the program to generate the same hash code as previously.
 Third generation: The antivirus software of this generation are the memory-resident programs that do not take into account the structure of viruses or heuristic rules to identify them. Rather, they scan the program to look for a small set of actions that indicate the infection and then deal with the viruses. An advantage is that it is not required to maintain any signatures or rules for a wide range of viruses in order to detect an infection.
Third generation: The antivirus software of this generation are the memory-resident programs that do not take into account the structure of viruses or heuristic rules to identify them. Rather, they scan the program to look for a small set of actions that indicate the infection and then deal with the viruses. An advantage is that it is not required to maintain any signatures or rules for a wide range of viruses in order to detect an infection.
 Fourth generation: The antivirus software of this generation are the packages that use scanning and activity trapping components in conjunction. These packages also comprise the access control capability, which restricts the viruses from entering into the system and updating the files for spreading the infection. All these features collectively strengthen the ability of the antivirus software.
Fourth generation: The antivirus software of this generation are the packages that use scanning and activity trapping components in conjunction. These packages also comprise the access control capability, which restricts the viruses from entering into the system and updating the files for spreading the infection. All these features collectively strengthen the ability of the antivirus software.
16. What is digital immune system? Explain how it works.
Ans.: With the increased use of Internet-based capabilities such as integrated mail systems (Lotus Notes and Microsoft Outlook) and mobile-program systems (Java and ActiveX), the threat of Internet-based virus propagation has also risen. Therefore, IBM has developed the digital immune system in response to these Internet-based virus threats. The goal of this system is to offer a very fast response time so that the viruses can be removed instantly as they enter into the system. Whenever a new virus is introduced into an organization, it is automatically captured by the digital immune system, which then examines it, adds detection and shielding for it and removes it from the system. The immune system also passes the information related to that virus to the other systems that are running the IBM antivirus, so that those systems can detect this virus before it begins to run.
The operation of the digital immune system involves the following steps (see Figure 10.2):
1. The monitoring program installed on each client machine in the organization detects the presence of a virus using various heuristic rules based on system behaviour, virus signatures or unexpected changes in the programs. In case any program on a client machine is found infected by a virus, the monitoring program sends a copy of that program to the administrative machine within the organization.
2. The administrative machine encrypts the copy of infected program received from monitoring program and forwards it to a central virus analysis machine.
3. The virus analysis machine is responsible for analyzing the infected program to detect new viruses. It creates an environment in which the infected program can be executed and analyzed. During execution, the structure and behaviour of the virus is analyzed and, based on this analysis, a virus signature is extracted. Now, the virus analysis machine examines the infected program for the extracted signature and produces a prescription for identifying and removing that virus.
4. The prescription produced by the virus analysis machine is then sent back to the administrative machine from where the infected program came.
5. The administrative machine sends the prescription to the infected client machine as well as to other client machines in the organization.
6. The prescription is also forwarded to all the subscribers and the individual user who are outside the organization network, so that they too can protect their systems from the new virus.
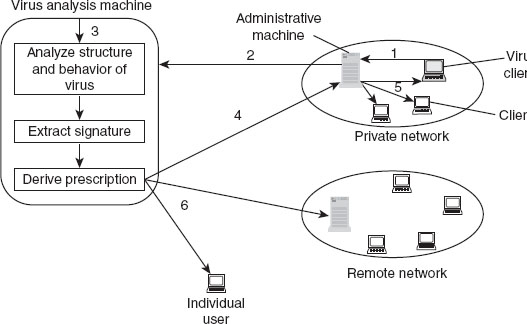
Figure 10.2 Operation of Digital Immune System
17. Discuss on behaviour-blocking software?
Ans.: Behaviour-blocking software is an approach to countering viruses that, unlike other approaches, is integrated with the operating system of a host computer. To detect a program for viral infections, it monitors the behaviour of a program in real time to determine any malicious actions. In case any attempt for a malicious action is detected, the behaviour-blocking software blocks the malicious action before it can affect the system. Certain malicious actions for which a program is analyzed are as follows:
 Attempts for viewing, opening, deleting and modifying files
Attempts for viewing, opening, deleting and modifying files
 Attempts for formatting disk drives
Attempts for formatting disk drives
 Starting network communications
Starting network communications
 Changes in important system settings
Changes in important system settings
 Changes in the logic of executable files.
Changes in the logic of executable files.
Behaviour-blocking software can block the malicious behaviours of a program in real time and/or terminate the entire program if it detects that the program may cause threat as it executes. The advantage of this software over other antivirus approaches is that it is able to detect and then block the malicious actions even if the instructions of a malicious code are modified or rearranged in order to evade detection. However, the disadvantage is that the as behaviours of a malicious code can be identified only after actually executing it on the machine, the malicious code may cause severe destruction to the system before its behaviours have been detected and blocked by the behaviour-blocking software.
18. What do you mean by firewall? Describe its characteristics.
Ans.: The progressive use of the Internet in organizations has opened up possibilities for the outside world to interact with internal networks, creating a great threat to the organization. Usually, organizations have huge amount of confidential data, leaking of which may prove to be a serious setback. Moreover, it is also necessary to protect the internal network against malicious programs such as virus and worms. Therefore, some mechanism is needed to ensure that the valuable data within the organization remains inside, as well as that outside attackers cannot break the security of the internal network.
A firewall is a mechanism that protects and isolates the internal network from the outside world. Simply put, a firewall prevents certain outside connections from entering into the network. It traps inbound or outbound packets, analyses them, and then permits access or discards them. Basically, a firewall is a router or a group of routers and computers that filter the traffic and implement access control between an un-trusted network (Internet) and the more trusted internal networks. Depending on the criteria used for filtering traffic, there are three common types of firewalls: packet filters (or packet-filtering router), application-level gateways and circuit-level gateways.
The characteristics of a firewall are as follows:
 A firewall specifies a single choke point by consolidating all the security-related capabilities into a single system or a set of systems. This results in simplified security management.
A firewall specifies a single choke point by consolidating all the security-related capabilities into a single system or a set of systems. This results in simplified security management.
 The choke point stops vulnerable services from entering or exiting through the network, prevents the intruders from accessing the protected network and protects against attacks such as IP spoofing.
The choke point stops vulnerable services from entering or exiting through the network, prevents the intruders from accessing the protected network and protects against attacks such as IP spoofing.
 It provides support for performing various Internet functions such as mapping a local address to an Internet address or maintaining logs for recording the usage of Internet, etc.
It provides support for performing various Internet functions such as mapping a local address to an Internet address or maintaining logs for recording the usage of Internet, etc.
 Virtual private networks can be implemented using firewalls.
Virtual private networks can be implemented using firewalls.
 A firewall specifies a single location from where all security-related events can be monitored and analyzed. Alarms and audits can also be used with firewall systems to protect against unauthorized events.
A firewall specifies a single location from where all security-related events can be monitored and analyzed. Alarms and audits can also be used with firewall systems to protect against unauthorized events.
19. List some limitations of firewalls.
Ans.: Though the firewall is an effective means of providing security to an organization, it has certain limitations, which are as follows:
 A firewall provides effective security to the internal network if it is configured as the only entry-exit point in the organization. However, if there are multiple entry-exit points in the organization and firewall is implemented at just one of them, then the incoming or outgoing traffic may bypass the firewall. This makes the internal network susceptible to attack through the points where the firewall has not been implemented.
A firewall provides effective security to the internal network if it is configured as the only entry-exit point in the organization. However, if there are multiple entry-exit points in the organization and firewall is implemented at just one of them, then the incoming or outgoing traffic may bypass the firewall. This makes the internal network susceptible to attack through the points where the firewall has not been implemented.
 A firewall is designed to protect against outside attacks. However, it does not have any mechanism to protect against internal threats such as an employee of a company who unknowingly helps an external attacker.
A firewall is designed to protect against outside attacks. However, it does not have any mechanism to protect against internal threats such as an employee of a company who unknowingly helps an external attacker.
 The firewall does not provide protection against any virus-infected program or files being transferred through the internal network. This is because it is almost impossible to scan all the files entering in the network for viruses. To protect the internal network against virus threats, a separate virus detection and removal strategy should be used.
The firewall does not provide protection against any virus-infected program or files being transferred through the internal network. This is because it is almost impossible to scan all the files entering in the network for viruses. To protect the internal network against virus threats, a separate virus detection and removal strategy should be used.
20. Discuss the packet-filtering router firewall.
Ans.: A packet-filtering router, also known as screening router or screening filter, is the one of the oldest firewall technologies that operates at the network layer. It examines the incoming and outgoing packets by applying a fixed set of rules on them and, thus, determines whether to forward the packets or to reject them. The rules used for filtering the packets are defined based on the following information contained in a network (IP) packet.
 The IP address of the system from where the packet has come
The IP address of the system from where the packet has come
 The IP address of the system for which the packet is destined
The IP address of the system for which the packet is destined
 The transport layer protocol used such as TCP or UDP
The transport layer protocol used such as TCP or UDP
 Transport-level address (that is, port number) of source and destination, which identifies the application such as Telnet or SNMP
Transport-level address (that is, port number) of source and destination, which identifies the application such as Telnet or SNMP
 The interface of the router where the packet came from or is destined to.
The interface of the router where the packet came from or is destined to.
The filtering rules specify which packets are allowed to pass through and in which direction they should flow, that is, from external to internal network or vice versa. Each rule has a specified action associated with it, either to allow or to deny a packet. Thus, there are two sets of filtering rules: allow, which permits the traffic, and deny, which discards the traffic. While examining a packet, if a match is found with any of the allow set of rules, then the packet is forwarded to the desired destination. On the other hand, if a match is found with any of the deny set of rules, the packet is discarded. In case no match is found, the default action is taken. The default policy can be either to forward or discard the packet. The former default policy provides more ease of use to the end users; however, it offers a reduced level of security. In contrast, the latter default policy is more conservative; however, it provides more security. Therefore, generally, the implementation of a firewall is initiated with default discard policy and, later, packet filtering is enforced by applying the rules one by one.
Advantages
Some advantages of packet filters are as follows:
 They are simple, since a single rule is enough to indicate whether to allow or deny the packet.
They are simple, since a single rule is enough to indicate whether to allow or deny the packet.
 They are transparent to the users; the users need not know the existence of packet filters.
They are transparent to the users; the users need not know the existence of packet filters.
 They operate at a fast speed as compared to other techniques.
They operate at a fast speed as compared to other techniques.
 The client computers need not be configured specially while implementing packet-filtering firewalls.
The client computers need not be configured specially while implementing packet-filtering firewalls.
 They protect the IP addresses of internal hosts from the outside network.
They protect the IP addresses of internal hosts from the outside network.
Disadvantages
Some disadvantages of packet filters are as follows:
 They are unable to inspect the application layer data in the packets and thus, cannot restrict access to ftp services.
They are unable to inspect the application layer data in the packets and thus, cannot restrict access to ftp services.
 It is a difficult task to set up the packet-filtering rules correctly.
It is a difficult task to set up the packet-filtering rules correctly.
 They lack support for authentication and have no alert mechanisms.
They lack support for authentication and have no alert mechanisms.
 Being stateless in nature, they are not well suited to application layer protocols.
Being stateless in nature, they are not well suited to application layer protocols.
21. What kind of attacks is possible on packet-filtering firewalls. Suggest appropriate countermeasures.
Ans.: Though packet-filtering firewalls operate at a fast speed and do not require users to be aware of packet filters, they are still prone to some attacks, which are as follows:
 IP address spoofing: In this attack, an intruder external to the organization's network sends a packet towards the network. The IP address of this packet is the same as that of one of the hosts in the network. The attacker thinks that he or she can penetrate into the internal network by spoofing IP address and, therefore, can attack on the systems easily. To prevent such attacks, packet-filtering firewalls should discard all the packets coming to the organization's network, which contains the IP address of any internal host.
IP address spoofing: In this attack, an intruder external to the organization's network sends a packet towards the network. The IP address of this packet is the same as that of one of the hosts in the network. The attacker thinks that he or she can penetrate into the internal network by spoofing IP address and, therefore, can attack on the systems easily. To prevent such attacks, packet-filtering firewalls should discard all the packets coming to the organization's network, which contains the IP address of any internal host.
 Source routing attack: In this attack, an intruder specifies the pre-defined route that a packet should take to reach its destination by selecting a particular option in the IP packet header. By choosing such an option, the intruder hopes that the packet-filtering firewall will bypass the security measures of checking the source routing information. The countermeasure for this attack is that packet-filtering firewalls should discard all the packets that are using this option.
Source routing attack: In this attack, an intruder specifies the pre-defined route that a packet should take to reach its destination by selecting a particular option in the IP packet header. By choosing such an option, the intruder hopes that the packet-filtering firewall will bypass the security measures of checking the source routing information. The countermeasure for this attack is that packet-filtering firewalls should discard all the packets that are using this option.
 Tiny fragment attack: In this attack, an intruder takes advantage of the IP packet fragmentation option and intentionally divides the original IP packet into small fragments. This is done to force the TCP header information to go into a separate packet fragment. The intruder hopes that the filtering rules that are based on the TCP header information can be circumvented this way, and that the packet-filtering firewall can be fooled such that it will examine only the first fragment of the packet and the rest will bypass through it without any checks. This attack can be prevented by discarding all the fragmented packets that are using TCP as the upper-layer protocol type.
Tiny fragment attack: In this attack, an intruder takes advantage of the IP packet fragmentation option and intentionally divides the original IP packet into small fragments. This is done to force the TCP header information to go into a separate packet fragment. The intruder hopes that the filtering rules that are based on the TCP header information can be circumvented this way, and that the packet-filtering firewall can be fooled such that it will examine only the first fragment of the packet and the rest will bypass through it without any checks. This attack can be prevented by discarding all the fragmented packets that are using TCP as the upper-layer protocol type.
22. Write a short note on application-level gateways.
Ans.: An application-level gateway operates at the application layer of the OSI model. It is also termed as a proxy server (or simply called proxy), which handles the flow of application-level traffic. The operation of application-level gateways is as follows:
1. A user contacts the application gateway with the help of a TCP/IP application such as Telnet, FTP or HTTP.
2. In response, the application gateway asks the user for the name, IP address and other information about the remote host that is to be accessed. It also asks the user to present its user ID and password to access the gateway.
3. The user supplies a valid user ID, password and other desired information to the gateway.
4. After verifying the user, the application gateway contacts the application running on the remote host on behalf of the user. The TCP segments comprising the application data are exchanged between the two end points.
5. Now, the application gateway serves as a proxy of the original user and delivers application data in both directions, from remote host to the user and vice versa.
Advantages
Application-level gateways are considered the most secure type of firewalls since they provide a number of advantages, which are as follows:
 The entire communication between the internal and external network happens only through the application gateways. This protects the internal IP addresses from the external network.
The entire communication between the internal and external network happens only through the application gateways. This protects the internal IP addresses from the external network.
 The use of application gateways provides transparency between the users and the external network.
The use of application gateways provides transparency between the users and the external network.
 They understand and implement high-level protocols such as HTTP and FTP.
They understand and implement high-level protocols such as HTTP and FTP.
 They support functions such as user authentication, caching, auditing and logging.
They support functions such as user authentication, caching, auditing and logging.
 They can process and manipulate the packet data.
They can process and manipulate the packet data.
 Strong user authentication can be enforced with application gateways.
Strong user authentication can be enforced with application gateways.
 They can disallow access to certain network services and allow others at the same time.
They can disallow access to certain network services and allow others at the same time.
Disadvantages
Some disadvantages of application-level gateways are as follows:
 Each new network service requires a number of proxy services to be added. Thus, application-level gateways are not scalable.
Each new network service requires a number of proxy services to be added. Thus, application-level gateways are not scalable.
 The addition of proxy services causes client applications to be modified.
The addition of proxy services causes client applications to be modified.
 Application gateways operate at a slower speed and, as a result, network performance degrades.
Application gateways operate at a slower speed and, as a result, network performance degrades.
 As they rely on the support provided by the underlying operating system, they are vulnerable to the bugs in the system.
As they rely on the support provided by the underlying operating system, they are vulnerable to the bugs in the system.
23. When the system administrator trusts the internal users, what type of firewall is to be used? What are its advantages and disadvantages?
Ans.: For a situation where the system administrator trusts the internal users, circuit-level gateways are the best suited. Circuit-level firewalls operate in a similar manner as that of packet-filtering firewalls, except that they operate at the session and transport layers of the OSI model. Whenever a session is to be established between a host in the internal network and a host outside the internal network, two TCP connections are to be established, one between the TCP user in the internal network and the circuit-level gateway, and another between the circuit-level gateway and the TCP user in the external network. After both the connections have been established, the circuit-level gateway forwards the packet from one connection to another without inspecting their contents. This is because, in circuit-level gateways, the session is validated before opening the connections. Thus, there is no need to examine the packet contents once the session has been established.
Circuit-level gateways maintain a virtual table to store session-related information of all the valid connections. This information includes the session date, a unique session identifier, connection state, IP addresses of source and destination, the sequencing information and the physical network interface through which the packet has come and has to go. Rather than allowing all packets that meet the rule set requirements to pass, it allows only those packets that are part of a valid, established connection.
Advantages
Some advantages of circuit-level gateways are as follows:
 They operate at a faster speed as compared to application-level gateways.
They operate at a faster speed as compared to application-level gateways.
 They offer more security than packet filters.
They offer more security than packet filters.
 They are not subject to IP address spoofing attacks.
They are not subject to IP address spoofing attacks.
 They perform network address translation (NAT) by changing source node IP address to its own and, thus, protecting internal host IP addresses from the external network.
They perform network address translation (NAT) by changing source node IP address to its own and, thus, protecting internal host IP addresses from the external network.
Disadvantages
Some disadvantages of circuit-level gateways are as follows:
 They are unable to perform security checks on higher-level protocols.
They are unable to perform security checks on higher-level protocols.
 They can restrict access only to TCP protocol subsets.
They can restrict access only to TCP protocol subsets.
 They have only a confined audit event generation capability.
They have only a confined audit event generation capability.
24. What is the role of bastion host?
Ans.: A bastion host is a system in an organization's internal network that acts as a vital point in the security of the network. This system is distinguished from other systems by the firewall administrator and serves as a platform for an application-level or circuit-level gateway. The hardware platform of the bastion host executes a secured version of the operating system and, therefore, behaves like a trusted system. Moreover, only limited proxy applications that are considered necessary by the network administrator, such as Telnet, DNS and SMTP, are installed on the bastion host. It requires additional authentication if any user wants access to these proxy services, and each proxy service needs its own authentication. Thus, the role of bastion host is to enhance the security of the network, so that it becomes more difficult for intruders to gain access to the internal network.
25. Describe the common types of firewall configurations.
Ans.: Firewalls may be implemented as a single system, such as a single packet filter or a single application gateway, or it may be implemented as a combination of packet filters and application gateways. There are three possible firewall configurations, which are as follows:
 Screened host firewall, single-homed bastion: In this firewall configuration, a packet filter and an application gateway (bastion host) are used in combination. The packet filter checks the traffic from the Internet to the internal corporate network and from the internal corporate network to the Internet, based on the specific rule. It allows packets from outside the network to enter the internal network if it is destined for the application gateway. Similarly, it allows packets from the internal network to move to the outside network only if the packet has originated from the application gateway. The application gateway is responsible for performing authentication and proxy functions.
Screened host firewall, single-homed bastion: In this firewall configuration, a packet filter and an application gateway (bastion host) are used in combination. The packet filter checks the traffic from the Internet to the internal corporate network and from the internal corporate network to the Internet, based on the specific rule. It allows packets from outside the network to enter the internal network if it is destined for the application gateway. Similarly, it allows packets from the internal network to move to the outside network only if the packet has originated from the application gateway. The application gateway is responsible for performing authentication and proxy functions.
This firewall configuration enhances the security of the network by implementing both packet-level and application-level filtering. The intruder now has to penetrate two separate firewalls in order to breach the security of the network. Moreover, it allows the network administrator more freedom in defining security policy. However, the demerit of this configuration is that internal hosts are connected to the packet filter as well as the application gateway. Therefore, if the security of the packet filter router is compromised, then an intruder can gain access to the whole internal network.
 Screened host firewall, dual-homed bastion: In this firewall configuration, the internal hosts of the network are not directly connected to the packet filter. Rather, the packet filter is directly connected only to the application gateway, which has separate connections with the internal hosts. This arrangement overcomes the problem of a screened host, single-homed bastion configuration. Thus, even if the packet filter is successfully attacked by an intruder, he or she gains access only to the application gateway and not to the whole network.
Screened host firewall, dual-homed bastion: In this firewall configuration, the internal hosts of the network are not directly connected to the packet filter. Rather, the packet filter is directly connected only to the application gateway, which has separate connections with the internal hosts. This arrangement overcomes the problem of a screened host, single-homed bastion configuration. Thus, even if the packet filter is successfully attacked by an intruder, he or she gains access only to the application gateway and not to the whole network.
 Screened subnet firewall: In this firewall configuration, two packet filters and one application gateway are used. One of the packet filters connects the outside network with the application gateway and other packet filter connects the internal hosts with the application gateway. It is the most secured type of configuration as an intruder has to attack three levels before gaining an access to the internal network.
Screened subnet firewall: In this firewall configuration, two packet filters and one application gateway are used. One of the packet filters connects the outside network with the application gateway and other packet filter connects the internal hosts with the application gateway. It is the most secured type of configuration as an intruder has to attack three levels before gaining an access to the internal network.
26. What do you understand by a trusted system?
Ans.: A computer and operating system that can be relied upon to a determined level to implement a given security policy is referred to as a trusted system. In other words, a trusted system is defined as the one system whose failure may cause a specified security policy to be compromised. Trusted systems are of prime importance in areas where it is required to protect the system resources or the information on the basis of levels of security defined; that is, where multilevel security is needed. For example, in military, the information is classified into various levels such as unclassified (U), confidential (C), secret (S) and top secret (TS), and each user is allowed to access only certain levels of information. In addition to military, the trusted systems are also being prominently used nowadays in banking and financial areas.
Central to the trusted systems is the reference monitor, which is an entity residing in the operating system of a computer and entrusted the responsibility of making all the access-control-related decisions on the basis of the defined security levels. The reference monitor is expected to be tamperproof, always invoked and subject to independent testing.
Multiple-choice Questions
1. Which of the following is a type of intruder?
(a) Masquerader
(b) Misfeasor
(c) Clandestine user
(d) All of these
2. The __________ strategy aware all the users about the importance of non-guessable or strong passwords.
(a) User education
(b) Reactive password checking
(c) Proactive password checker
(d) None of these
3. A virus is a computer __________.
(a) File
(b) Network
(c) Program
(d) Database
4. A __________ replicates itself by creating its own copies, in order to bring the network to a halt.
(a) Worm
(b) Virus
(c) Trojan horse
(d) Logic bomb
5. The __________ generation of antivirus software uses heuristic scanners.
(a) First
(b) Second
(c) Third
(d) Fourth
6. The digital immune system was developed by __________.
(a) HCL
(b) IEEE
(c) ANSI
(d) IBM
7. The firewall should be situated __________.
(a) Outside a network
(b) Inside a network
(c) Between a network and the outside world
(d) None of these
8. __________ firewall is mostly used in small businesses.
(a) Packet-filtering
(b) Circuit-level gateway
(c) Application-level gateway
(d) None of these
9. Circuit-level gateways are __________ as compared to packet filters.
(a) Less secure
(b) More secure
(c) Slower
(d) None of these
10. The trap set to attract the potential intruders is known as __________.
(a) Honeypot
(b) Trapdoor
(c) Proxy
(d) All of these
Answers
1. (d)
2. (a)
3. (c)
4.(a)
5.(b)
6.(d)
7.(c)
8.(a)
9.(b)
10.(a)
A
Advanced Encryption Standard (AES), 56–58
AES. See Advanced Encryption Standard (AES)
AH. See Authentication Header (AH)
alert protocol, 161
algebraic structure, 19
antivirussoftware, 176
application-level gateways, 180–181
arbitrated digital signature, 114–115
asymmetric-key cryptography, 76
characteristics of, 76
asymmetric-key encipherment, 11
audit records, 169
Authentication Header (AH), 151–152
avalanche effect, 51
B
bastion host, 182
behavior-blocking software, 178
birthday bound, 95
birthday paradox, 95
bit-oriented cipher, 33
boot sector virus, 173
C
Caesar cipher, 26
certificate renewable, 137–138
Certificate Revocation List (CRL), 137
change cipher spec protocol, 161
Chinese Remainder Theorem (CRT), 69–70
chosen-ciphertext attack, 77–78
Cipher Block Chaining (CBC) mode, 62
Cipher Feedback (CFB)mode, 62–63
cipher key, 45
ciphers, 10
ciphertext, 9
classical encryption techniques, 25
different categories of, 25
columnar transposition cipher, 32
common modulus attack, 78
completeness effect, 51
compression function, 96
congruence, 17
conventional encryption model, 24–25
issuesin, 25
co-prime, 65
CRT. See Chinese Remainder Theorem (CRT)
cryptography, 9
D
Data Encryption Standard (DES), 45
strength of, 49
decryption, 10
DES. See Data Encryption Standard (DES)
detection-specific audit records, 169
differential cryptanalysis, 50
Diffie-Hellman key exchange algorithm, 81–82
advantages of, 82
limitations of, 82
diffusion, 35
digital immune system, 176–177
attacks on, 113
process of, 112
properties and requirements of, 113
Digital Signature Standard (DSS), 117–119
direct digital signature, 114
directory authentication service, 138
discrete logarithmic problems, 70–71
distributed intrusion detection, 170
architecture of, 170
distributed intrusion detection systems, 170–171
DSS. See Digital Signature Standard (DSS)
E
ECC. See elliptic curve cryptosystem (ECC)
Electronic Code Book (ECB) mode, 61
ElGamal algorithm, 85
attacks on, 85
encryption and decryption process, 83–84
ElGamal encryption system, 83–84
elliptic curve cryptosystem (ECC), 86
elliptic curves, 85
Encapsulating Security Payload (ESP), 151
encryption, 10
transport and tunnel mode of, 155–157
ESP. See Encapsulating Security Payload (ESP)
Euler's totient function, 66
F
factorization attack, 77
Federal Information Processing Standard (FIPS 186), 117–119
model of, 36
file-infecting virus, 173
firewall, 178
limitations of, 178
firewall configurations, 182–83
forwardable ticket, 135
G
group, 19
H
hash function, 93
hash-based MAC (HMAC), 106–109
design objectives of, 107
HMAC. See Hash-based MAC (HMAC)
honeypots, 171
I
IDEA. See International Data
Encryption Algorithm (IDEA)
IKE. See Internet Key Exchange (IKE)
Improved PES (IPES), 53
International Data Encryption Algorithm (IDEA), 53
Internet Key Exchange (IKE), 157
Internet Security Association and Key Management Protocol (ISAKMP), 159
header format of, 159
intruders, 167
intrusion detection, 168
intrusion techniques, 167
IP address spoofing, 180
IPES. See Improved PES (IPES)
ISAKMP. See Internet Security Association and Key Management Protocol (ISAKMP)
iterated hash functions, 96
K
Kerberos
Kerberos principal, 131
Kerberos realm, 131
key, 10
key clustering, 50
key management, 14
functions of, 14
rules for maintaining, 14
keyed transposition cipher, 25, 32
keyless transposition cipher, 25, 31
L
logic bomb, 175
M
MAC. See message authentication code (MAC)
malicious software, 173
man-in-the-middle attack, 83
MD5 (message digest, version 5), 96–99
meet-in-the-middle attack, 52
message authentication, 91
attacks on, 91
types of authentication, 91
message authentication code (MAC), 92–93
Miller-Rabin algorithm, 68
modular arithmetic, 16
monoalphabetic cipher, 25
different techniques of, 25
multiplicative cipher, 27
mutual authentication protocol, 121–124
N
National Institute of Standards and Technology (NIST), 45
native audit records, 169
NESSIE. See New European Schemes for Signatures, Integrity, and Encryption (NESSIE)
New European Schemes for Signatures, Integrity, and Encryption (NESSIE), 104
NIST. See National Institute of Standards and Technology (NIST)
non-Feistel cipher, 38
O
onetime pad, 33
one-way authentication protocol, 124–125
Output Feedback (OFB) mode, 63–64
P
packet-filtering router, 179–180
passive attack, 2
password protection approaches, 168
password selection strategies, 172
PES. See Proposed Encryption Standard (PES)
PGP. See pretty good privacy (PGP)
plaintext, 9
plaintext attack, 78
polyalphabetic ciphers, 25, 28
technique of, 28
polymorphic virus, 173
possible weak keys, 50
postdatable ticket, 135
pretty good privacy (PGP), 139–142
concept of trust and legitimacy, 142–143
general format of, 145
key rings and, 142
steps followed for transmission and reception of, 142
structure of key rings of, 143–145
prime number, 65
private key, 112
product cipher, 36
Proposed Encryption Standard (PES), 53
public announcement, 78
public directory, 78
public-key authority, 79
public-key certificates, 79–80
public-key cryptography, 80–81
distribution of secret keys using, 80–81
public-key encryption technique, 125
R
Rabin-Miller test. See Miller-Rabin algorithm
renewable ticket, 135
ring, 19
RSA digital signature scheme, 115–117
S
secret key, 113
Secure Electronic Transaction (SET), 162–164
Secure Hash Algorithm (SHA), 99–103
Secure Hash Standard (SHS), 99
Secure Socket Layer (SSL), 160–161
secure/multipurpose Internet mail extension (S/MIME), 146–149
semi-weak keys, 50
SHA. See Secure Hash Algorithm (SHA)
Shannon's theory of diffusion and confusion, 35
shift cipher, 26
SHS. See Secure Hash Standard (SHS)
source routing attack, 180
spyware, 175
SSL record protocol, 160
steganography, 15
stream cipher, 32
substitution cipher, 25
symmetric-key cipher, 24
symmetric-key encipherment, 10
symmetric-key encryption technique, 124–125
T
timing attack, 78
tiny fragment attack, 180
Transport Layer Security (TLS), 162
transposition cipher, 25
Trojan horse, 175
trusted system, 183
V
Vigenere cipher, 30
Vital Information Resources Under Seize (Virus), 173–174
W
weak keys, 50
Whirlpool, 104
Whirlpool cryptographic hash function, 104–106
X
certificate renewable and, 137–138
certificate revocation and, 137–138
authentication procedure of, 138–139


Copyright © 2012 Dorling Kindersley (India) Pvt. Ltd
This book is sold subject to the condition that it shall not, by way of trade or otherwise, be lent, resold, hired out, or otherwise circulated without the publisher's prior written consent in any form of binding or cover other than that in which it is published and without a similar condition including this condition being imposed on the subsequent purchaser and without limiting the rights under copyright reserved above, no part of this publication may be reproduced, stored in or introduced into a retrieval system, or transmitted in any form or by any means (electronic, mechanical, photocopying, recording or otherwise), without the prior written permission of both the copyright owner and the publisher of this book.
ISBN 978-81-317-6452-7
First Impression
Published by Dorling Kindersley (India) Pvt. Ltd, licensees of Pearson Education in South Asia.
Head Office: 7th Floor, Knowledge Boulevard, A-8(A), Sector 62, Noida 201 309, UP, India.
Registered Office: 11 Community Centre, Panchsheel Park, New Delhi 110 017, India.
Compositor: Cameo Corporate Services Ltd., Chennai.
Printer: xxx.
Today, the Internet has undoubtedly become the largest public data network that facilitates personal and business communications worldwide. The amount of traffic moving through the Internet as well as corporate networks is growing day by day. More and more people are communicating via e-mails, branch offices are using the Internet to remotely connect to their corporate networks and most commercial transactions such as shopping, bill payments and banking are also being done through the networks. Due to growing dependency of users, businesses and organizations on computer networks, it has become important to protect the information being exchanged from various security attacks. In addition, the confidentiality, authenticity and integrity of the messages moving across the networks must be ensured. This is where network security is important.
Network security is a set of protocols that facilitates the use of networks without any fear of security attacks. The most common and traditional technique used for providing network security is cryptography, which is a process of transforming messages into an unintelligible form before transmitting and converting them back to the original when received by the receiver. However, with the evolution of cryptography and network security disciplines, more practical and readily available applications such as Kerberos, Pretty Good Privacy (PGP), IPSec, Secure Socket Layer (SSL), Transport Layer Security (TLS) and firewalls have developed to implement the network security. Keeping in mind the importance of network security, almost all universities have integrated the study of cryptography and network security in B.Tech. (CSE and IT), MCA and MBA courses. The book in your hands, Cryptography and Network Security, in its unique easy-to-understand question-and-answer format directly addresses the need of students enrolled in these courses.
The book comprises questions and their corresponding answers on the basic issues to be addressed by cryptography and network security capability as well as practical applications that are being used for providing network security. The text has been designed to make it particularly easy for students to understand the principles and practice of cryptography and network security. An attempt has been made to make the book self-contained so that students can learn the subject by themselves. The organized and accessible format allows students to quickly find questions on specific topics.
The book Cryptography and Network Security is a part of series named Pearson Instant Learning Series (PILS), which has a number of books designed as quick reference guides.
Unique Features
1. Designed as a student friendly self-learning guide, the book is written in a clear, concise and lucid manner.
2. Easy-to-understand question-and-answer format.
3. Includes previously asked as well as new questions organized in chapters.
4. All types of questions including multiple-choice questions, short and long questions are covered.
5. Solutions to numerical questions asked at examinations are provided.
6. All ideas and concepts are presented with clear examples.
7. Text is well structured and well supported with suitable diagrams.
8. Inter-chapter dependencies are kept to a minimum.
9. A comprehensive index at the end of the book for quick access to desired topics.
Chapter Organization
All the questions-answers are organized into ten chapters. A brief description of these chapters is as follows:
 Chapter 1 provides an overview of basic concepts of network security. It discusses the need, goals and principles of network security as well as different kinds of attacks on computer systems and network. It also gives a brief idea of security services and security mechanisms.
Chapter 1 provides an overview of basic concepts of network security. It discusses the need, goals and principles of network security as well as different kinds of attacks on computer systems and network. It also gives a brief idea of security services and security mechanisms.
 Chapter 2 introduces the concept of cryptography, which is the most common technique used for providing network security. It describes important mathematical principles that are central to the design of ciphers. The chapter further discusses modular arithmetic, which is the fundamental concept to understand the working of ciphers. It also discusses the concept of cryptanalysis and various cryptanalysis attacks.
Chapter 2 introduces the concept of cryptography, which is the most common technique used for providing network security. It describes important mathematical principles that are central to the design of ciphers. The chapter further discusses modular arithmetic, which is the fundamental concept to understand the working of ciphers. It also discusses the concept of cryptanalysis and various cryptanalysis attacks.
 Chapter 3 deals with symmetric-key ciphers. It starts with a discussion on traditional symmetric-key ciphers that include various substitution ciphers such as additive, shift, multiplicative, affine, autokey, Playfair, Vigenere and Hill cipher and transposition ciphers. Then, the discussion moves on to two important categories of ciphers, namely stream and block ciphers. The chapter also includes a brief discussion on Shannon's theory of diffusion and confusion. Finally, the chapter concludes with a discussion on product ciphers proposed by Shannon, and the two categories of product ciphers, namely Feistel and non-Feistel ciphers.
Chapter 3 deals with symmetric-key ciphers. It starts with a discussion on traditional symmetric-key ciphers that include various substitution ciphers such as additive, shift, multiplicative, affine, autokey, Playfair, Vigenere and Hill cipher and transposition ciphers. Then, the discussion moves on to two important categories of ciphers, namely stream and block ciphers. The chapter also includes a brief discussion on Shannon's theory of diffusion and confusion. Finally, the chapter concludes with a discussion on product ciphers proposed by Shannon, and the two categories of product ciphers, namely Feistel and non-Feistel ciphers.
 Chapter 4 concentrates on the symmetric-key algorithms, which include Data Encryption Standard (DES) and Advanced Encryption Standard (AES). The chapter presents a detailed study on the design and analysis of DES. It also explains the general structure and the key expansion algorithm of AES.
Chapter 4 concentrates on the symmetric-key algorithms, which include Data Encryption Standard (DES) and Advanced Encryption Standard (AES). The chapter presents a detailed study on the design and analysis of DES. It also explains the general structure and the key expansion algorithm of AES.
 Chapter 5 is based on the number theory, which provides a mathematical background required to understand the asymmetric-key cryptography. It covers several important concepts related to prime numbers such as Fermat's theorem, Euler's totient function, Euler's theorem, Miller-Rabin algorithm and Chinese Remainder theorem.
Chapter 5 is based on the number theory, which provides a mathematical background required to understand the asymmetric-key cryptography. It covers several important concepts related to prime numbers such as Fermat's theorem, Euler's totient function, Euler's theorem, Miller-Rabin algorithm and Chinese Remainder theorem.
 Chapter 6 deals with asymmetric-key algorithms, which include RSA, Diffie-Hellman algorithm, ElGamal encryption system and Elliptic curve cryptography (ECC).
Chapter 6 deals with asymmetric-key algorithms, which include RSA, Diffie-Hellman algorithm, ElGamal encryption system and Elliptic curve cryptography (ECC).
 Chapter 7 focuses on message authentication mechanisms used to ensure that the integrity of the received message has been preserved. It explains various authentication functions and message authentication code (MAC). It also gives a detailed description of standard hash functions such as MD5, SHA-1 and Whirlpool. The chapter also spells out the concept of birthday attacks against hash functions.
Chapter 7 focuses on message authentication mechanisms used to ensure that the integrity of the received message has been preserved. It explains various authentication functions and message authentication code (MAC). It also gives a detailed description of standard hash functions such as MD5, SHA-1 and Whirlpool. The chapter also spells out the concept of birthday attacks against hash functions.
 Chapter 8 familiarizes the reader with the concept of digital signatures, and presents the essential properties and requirements of digital signatures, possible attacks on digital signatures and various digital signature schemes including RSA, ElGamal and DSS. The chapter then shifts its focus on authentication protocol and discusses its two categories, namely mutual authentication and one-way authentication.
Chapter 8 familiarizes the reader with the concept of digital signatures, and presents the essential properties and requirements of digital signatures, possible attacks on digital signatures and various digital signature schemes including RSA, ElGamal and DSS. The chapter then shifts its focus on authentication protocol and discusses its two categories, namely mutual authentication and one-way authentication.
 Chapter 9 presents the working principle of Kerberos protocol, X.509 authentication service and its certificates. The chapter also describes the security at the application layer covering PGP and S/MIME, security at the transport layer covering SSL and TSL, and security at the network layer describing IPSec.
Chapter 9 presents the working principle of Kerberos protocol, X.509 authentication service and its certificates. The chapter also describes the security at the application layer covering PGP and S/MIME, security at the transport layer covering SSL and TSL, and security at the network layer describing IPSec.
 Chapter 10 provides a description on system security, covering the concepts of intrusion prevention and detection, Honeypots, malicious software, viruses, digital immune system, behaviour-blocking software, firewalls and trusted systems.
Chapter 10 provides a description on system security, covering the concepts of intrusion prevention and detection, Honeypots, malicious software, viruses, digital immune system, behaviour-blocking software, firewalls and trusted systems.
Acknowledgements
 Our publisher Pearson Education, their editorial team and panel reviewers for their valuable contributions toward content enrichment.
Our publisher Pearson Education, their editorial team and panel reviewers for their valuable contributions toward content enrichment.
 Our technical and editorial consultants for devoting their precious time to improve the quality of the book.
Our technical and editorial consultants for devoting their precious time to improve the quality of the book.
 Our entire research and development team who have put in their sincere efforts to bring out a high-quality book.
Our entire research and development team who have put in their sincere efforts to bring out a high-quality book.
Feedback
For any suggestions and comments about this book, please feel free to send an e-mail to itlesl@rediffmail.com.
Hope you enjoy reading this book as much as we have enjoyed writing it.
ROHIT KHURANA
Founder and CEO
ITL ESL
1. What is the need for network security? Explain its goals.
Ans.: During the last two decades, computer networks have revolutionized the use of information. Information is now distributed over the network. Authorized users can use computer networks for sending and receiving information from a distance. People can also perform various tasks such as shopping, bill payments and banking over a computer network. This implies that the computer networks are nowadays used for carrying personal as well as financial data. Thus, it becomes important to secure the network, so that unauthorized people cannot access such sensitive information.
For secure communication, there are some basic goals of network security that should be achieved. These are as follows:
 Confidentiality: This refers to maintaining the secrecy of the message being transmitted over a network. Only the sender and the intended receiver should be able to understand and read the message, and eavesdroppers should not be able to read or modify the contents of the message. To achieve confidentiality the message should be transmitted over the network in an encrypted form.
Confidentiality: This refers to maintaining the secrecy of the message being transmitted over a network. Only the sender and the intended receiver should be able to understand and read the message, and eavesdroppers should not be able to read or modify the contents of the message. To achieve confidentiality the message should be transmitted over the network in an encrypted form.
 Integrity: Any message sent over the network must reach the intended receiver without any modification made to it. If any changes are made, the receiver must be able to detect that some alteration has happened. Integrity can be achieved by attaching a checksum to the message. This checksum ensures that an attacker cannot alter the message and, hence, that integrity is preserved.
Integrity: Any message sent over the network must reach the intended receiver without any modification made to it. If any changes are made, the receiver must be able to detect that some alteration has happened. Integrity can be achieved by attaching a checksum to the message. This checksum ensures that an attacker cannot alter the message and, hence, that integrity is preserved.
 Availability: Information created and stored by an organization should be available all the time to authorized users, failing which the information ceases to be useful. Availability is also equally important for organizations, because unavailability of information can adversely affect an organization's day-to-day operations. For example, imagine the status/service of a bank if its customers are unable to make transactions using their accounts.
Availability: Information created and stored by an organization should be available all the time to authorized users, failing which the information ceases to be useful. Availability is also equally important for organizations, because unavailability of information can adversely affect an organization's day-to-day operations. For example, imagine the status/service of a bank if its customers are unable to make transactions using their accounts.
2. What are the principles of network security?
Ans.: The principles of network security include confidentiality, integrity, availability, nonrepudiation, access control and authentication.
 Confidentiality: Refer previous question.
Confidentiality: Refer previous question.
 Integrity: Refer previous question.
Integrity: Refer previous question.
 Availability: Refer previous question.
Availability: Refer previous question.
 Nonrepudiation: After a message has been sent and received, the sender and receiver should not be able to deny about the sending and receiving of the message, respectively. The receiver should be able to prove that the message has come from the intended sender and not from anyone else. In addition, the receiver should be able to prove that the received message's contents are the same as sent by the sender.
Nonrepudiation: After a message has been sent and received, the sender and receiver should not be able to deny about the sending and receiving of the message, respectively. The receiver should be able to prove that the message has come from the intended sender and not from anyone else. In addition, the receiver should be able to prove that the received message's contents are the same as sent by the sender.
 Access control: The term ‘access’ involves writing, reading, executing and modifying. Thus, access control determines and controls who can access what. It regulates which user has access to a resource, under what circumstances the access is possible and which operations the user can perform on that resource. For example, we can specify that user
Access control: The term ‘access’ involves writing, reading, executing and modifying. Thus, access control determines and controls who can access what. It regulates which user has access to a resource, under what circumstances the access is possible and which operations the user can perform on that resource. For example, we can specify that user A is allowed to only view the records in a database but not to modify them. However, user B is allowed to read as well as update the records.
 Authentication: Authentication is concerned with determining whom you are communicating with. Authentication is necessary to ensure that the receiver has received the message from the actual sender, and not from an attacker. That is, the receiver should be able to authenticate the sender, which can be achieved by sharing a common secret code word, by sending digital signatures or by the use of digital certificates.
Authentication: Authentication is concerned with determining whom you are communicating with. Authentication is necessary to ensure that the receiver has received the message from the actual sender, and not from an attacker. That is, the receiver should be able to authenticate the sender, which can be achieved by sharing a common secret code word, by sending digital signatures or by the use of digital certificates.
3. Define a network security attack?
Ans.: A network security attack refers to an act of breaching the security or authentication routines of a network. Such an act is a threat to the basic goals of secure communication, such as confidentiality, integrity and authentication.
4. Explain passive attacks and active attacks.
Ans.: Network security attacks can be classified into two categories—passive attacks and active attacks.
Passive Attacks
In a passive attack, the attacker indulges in eavesdropping, that is, listening to a communication channel and monitoring the contents of a message. The term ‘passive’ indicates that the main goal of the intruder is just to gather information and not to do any alteration to the message or harm the system resources. A passive attack is hard to recognize, as the message is not tampered with or altered; therefore, the sender and receiver remains unaware that the message contents have been read by another party. However, some measures such as encryption are available to prevent such attacks.
Two types of passive attacks are:
 Release of message contents: This type of passive attack involves (1) capturing the sensitive information that is sent via email or (2) tapping a conversation that is conducted over a telephone line.
Release of message contents: This type of passive attack involves (1) capturing the sensitive information that is sent via email or (2) tapping a conversation that is conducted over a telephone line.
 Traffic analysis: In this type of attack, an intruder observes the frequency and length of messages being exchanged between communicating nodes. A passive attacker can then use this information for guessing the nature of the communication that was taking place.
Traffic analysis: In this type of attack, an intruder observes the frequency and length of messages being exchanged between communicating nodes. A passive attacker can then use this information for guessing the nature of the communication that was taking place.
Active Attacks
In an active attack, an intruder either alters the original message or creates a fake message. This attack tries to affect the operation of system resources. When compared to passive attacks, it is easier to recognize an active attack, but harder to prevent it. Active attacks can be classified into four categories, as follows:
 Masquerade: In computer terms, ‘masquerading’ is said to happen when an entity impersonates another. In such an attack, an unauthorized entity tries to gain more privileges than it is authorized for. Masquerading is generally done by using stolen IDs and passwords, or through bypassing authentication mechanisms.
Masquerade: In computer terms, ‘masquerading’ is said to happen when an entity impersonates another. In such an attack, an unauthorized entity tries to gain more privileges than it is authorized for. Masquerading is generally done by using stolen IDs and passwords, or through bypassing authentication mechanisms.
 Replay: This active attack involves capturing a copy of the message sent by the original sender and retransmitting it later to bring about an unauthorized result.
Replay: This active attack involves capturing a copy of the message sent by the original sender and retransmitting it later to bring about an unauthorized result.
 Modification of messages: This attack involves making certain modifications to the captured message, or delaying or reordering the messages to cause an unauthorized effect.
Modification of messages: This attack involves making certain modifications to the captured message, or delaying or reordering the messages to cause an unauthorized effect.
 Denial of service (DoS): This attack prevents the normal functioning or proper management of communication facilities. For example, a network server can be overloaded by unwanted packets, thus resulting in performance degradation. DoS attacks can interrupt and slow down the services of a network, or even completely jam a network.
Denial of service (DoS): This attack prevents the normal functioning or proper management of communication facilities. For example, a network server can be overloaded by unwanted packets, thus resulting in performance degradation. DoS attacks can interrupt and slow down the services of a network, or even completely jam a network.
5. Explain various network security services.
Ans.: The International Telecommunication Union-Telecommunication Standardization Sector (ITU-T), also known as X.800, defines security service as ‘a service provided by a protocol layer of communicating open system, which ensures adequate security of the systems or of data transfers’. Another definition of security service is found in RFC 2828, which defines it as ‘a processing or communication service that is provided by a system to give a specific kind of protection to system resources; security services implement security policies and are implemented by security mechanisms’. According to X.800, security services are divided into five categories and 14 specific services (see Figure 1.1).

Figure 1.1 Security Services
 Authentication: This service provides the assurance that the communicating party at the other end of the line is the correct party. Two types of authentication services defined by X.800 are:
Authentication: This service provides the assurance that the communicating party at the other end of the line is the correct party. Two types of authentication services defined by X.800 are:
 Peer entity authentication: This provides authentication of the receiver or sender during the connection establishment phase in connection-oriented communication.
Peer entity authentication: This provides authentication of the receiver or sender during the connection establishment phase in connection-oriented communication.
 Data origin authentication: This service provides authentication of the data source in a connectionless communication.
Data origin authentication: This service provides authentication of the data source in a connectionless communication.
 Nonrepudiation: This service provides the assurance that the sender and receiver are not able to deny about the sending and receiving of the message, respectively. X.800 defines two types of services for nonrepudiation:
Nonrepudiation: This service provides the assurance that the sender and receiver are not able to deny about the sending and receiving of the message, respectively. X.800 defines two types of services for nonrepudiation:
 Origin nonrepudiation: This helps the receiver prove that the message was sent by the intended sender.
Origin nonrepudiation: This helps the receiver prove that the message was sent by the intended sender.
 Destination nonrepudiation: This helps the sender prove that the message was delivered to the intended receiver.
Destination nonrepudiation: This helps the sender prove that the message was delivered to the intended receiver.
 Data confidentiality: This service provides protection against the disclosure of data to unauthorized parties. For data confidentiality, X.800 defines four types of services:
Data confidentiality: This service provides protection against the disclosure of data to unauthorized parties. For data confidentiality, X.800 defines four types of services:
 Connection confidentiality: This provides confidentiality for all the messages transmitted between two users on a connection-oriented transmission, such as over a TCP connection.
Connection confidentiality: This provides confidentiality for all the messages transmitted between two users on a connection-oriented transmission, such as over a TCP connection.
 Connectionless confidentiality: This service provides confidentiality for all user data in a single data block.
Connectionless confidentiality: This service provides confidentiality for all user data in a single data block.
 Selective-field confidentiality: This provides confidentiality for a single message or some selected data fields of a message in a single data block or on a connection.
Selective-field confidentiality: This provides confidentiality for a single message or some selected data fields of a message in a single data block or on a connection.
 Traffic flow confidentiality: This provides confidentiality for the data derived from the traffic flow analysis.
Traffic flow confidentiality: This provides confidentiality for the data derived from the traffic flow analysis.
 Data integrity: This service provides assurance that data received by the receiver are exactly the same (with no modification, duplication, reordering, deletion or insertion) as sent by the authorized sender. For data integrity, the services defined by X.800 are as follows:
Data integrity: This service provides assurance that data received by the receiver are exactly the same (with no modification, duplication, reordering, deletion or insertion) as sent by the authorized sender. For data integrity, the services defined by X.800 are as follows:
 Connection integrity with recovery: This provides integrity to the entire user data or stream of messages on a connection. That is, it detects any modification, duplication, reordering, deletion, insertion or replay made to data or messages within an entire data or message sequence. If any change in data is detected, then this service tries to recover the original data.
Connection integrity with recovery: This provides integrity to the entire user data or stream of messages on a connection. That is, it detects any modification, duplication, reordering, deletion, insertion or replay made to data or messages within an entire data or message sequence. If any change in data is detected, then this service tries to recover the original data.
 Connection integrity without recovery: This service provides integrity to the entire user data or stream of messages on a connection. That is, it detects any change made to the messages or data, but does not try to recover the original data.
Connection integrity without recovery: This service provides integrity to the entire user data or stream of messages on a connection. That is, it detects any change made to the messages or data, but does not try to recover the original data.
 Selective-field connection integrity: This provides integrity to selected data fields within a block of user data or selected part of the message over a connection.
Selective-field connection integrity: This provides integrity to selected data fields within a block of user data or selected part of the message over a connection.
 Connectionless integrity: This provides integrity to a single data block or a single message in a connectionless communication and detects any modification made to data. It may also provide detection of replay attacks.
Connectionless integrity: This provides integrity to a single data block or a single message in a connectionless communication and detects any modification made to data. It may also provide detection of replay attacks.
 Selective-field connectionless integrity: This provides integrity of selected data fields within a block of user data in a connectionless communication and also detects any modification in these fields.
Selective-field connectionless integrity: This provides integrity of selected data fields within a block of user data in a connectionless communication and also detects any modification in these fields.
 Access control: This provides protection to data and resources from unauthorized access. This service defines the condition for accessing any data and controls the users who can access the resources.
Access control: This provides protection to data and resources from unauthorized access. This service defines the condition for accessing any data and controls the users who can access the resources.
6. Explain various security mechanisms. How are they related to security services?
Ans.: Security mechanisms have been defined by ITU-T (X.800). They are used to implement OSI security services and are incorporated into the suitable protocol layer. Some of the security mechanisms recommended by ITU-T (X.800) are shown in Figure 1.2.

Figure 1.2 Security Mechanisms
 Encipherment: This refers to the transformation of the message or data with the help of mathematical algorithms. The main aim of this mechanism is to provide confidentiality. The two techniques that are used for encipherment are cryptography and steganography.
Encipherment: This refers to the transformation of the message or data with the help of mathematical algorithms. The main aim of this mechanism is to provide confidentiality. The two techniques that are used for encipherment are cryptography and steganography.
 Data integrity: This refers to the method of ensuring the integrity of data. For this, the sender computes a check value by applying some process over the data being sent, and then appends this value to the data. On receiving the data, the receiver again computes the check value by applying the same process over the received data. If the newly computed check value is same as the received one, then it means that the integrity of data is preserved.
Data integrity: This refers to the method of ensuring the integrity of data. For this, the sender computes a check value by applying some process over the data being sent, and then appends this value to the data. On receiving the data, the receiver again computes the check value by applying the same process over the received data. If the newly computed check value is same as the received one, then it means that the integrity of data is preserved.
 Digital signature: This refers to the method of electronic signing of data by the sender and electronic verification of the signature by the receiver. It provides information about the author, date and time of the signature, so that the receiver can prove the sender's identity.
Digital signature: This refers to the method of electronic signing of data by the sender and electronic verification of the signature by the receiver. It provides information about the author, date and time of the signature, so that the receiver can prove the sender's identity.
 Authentication exchange: This refers to the exchange of some information between two communicating parties to prove their identity to each other.
Authentication exchange: This refers to the exchange of some information between two communicating parties to prove their identity to each other.
 Traffic padding: This refers to the insertion of extra bits into the stream of data traffic to prevent traffic analysis attempts by attackers.
Traffic padding: This refers to the insertion of extra bits into the stream of data traffic to prevent traffic analysis attempts by attackers.
 Routing control: This refers to the selection of a physically secured route for data transfer. It also allows changing of route if there is any possibility of eavesdropping on a certain route.
Routing control: This refers to the selection of a physically secured route for data transfer. It also allows changing of route if there is any possibility of eavesdropping on a certain route.
 Notarization: This refers to the selection of a trusted third party for ensuring secure communication between two communicating parties.
Notarization: This refers to the selection of a trusted third party for ensuring secure communication between two communicating parties.
 Access control: It refers to the methods used to ensure that a user has the right to access the data or resource.
Access control: It refers to the methods used to ensure that a user has the right to access the data or resource.
Security services and mechanisms share a close relationship with each other. One or more security mechanisms are used together to provide a security service. In addition, the same mechanism can also be used in many security services. Table 1.1 lists the security services along with the mechanisms that are used in these services.
| Security services | Security mechanisms |
|---|---|
| Authentication | Encipherment, digital signature and authentication exchange |
| Nonrepudiation | Data integrity, digital signature and notarization |
| Data confidentiality | Encipherment and routing control |
| Data integrity | Encipherment, data integrity, and digital signature |
| Access control | Access control mechanism |
7. Briefly explain the model for network security.
Ans.: With the phenomenal increase in the use of computer networks such as the Internet over the last few years, it has become essential to enhance the security of the network. To provide secured communication over the network, a general model of network security was created, which enhanced network security. This model consists of various components, which are as follows:
 Message: This is the information that is to be transmitted over the network.
Message: This is the information that is to be transmitted over the network.
 Principals: These refer to communication nodes, one which transmits the message (sender) and the other receives it (receiver).
Principals: These refer to communication nodes, one which transmits the message (sender) and the other receives it (receiver).
 Security-related transformation: This refers to the transformations made to the information to be sent, so that it is unreadable to an intruder. An example for such transformation includes either encryption of the message or inserting a message to verify the identity of the sender.
Security-related transformation: This refers to the transformations made to the information to be sent, so that it is unreadable to an intruder. An example for such transformation includes either encryption of the message or inserting a message to verify the identity of the sender.
 Secret information: This refers to the information that is shared between the two principals and used while applying the transformation at both the sender's and receiver's ends. For example, in case of encryption, the secret information can be a key used for encrypting and decrypting the message.
Secret information: This refers to the information that is shared between the two principals and used while applying the transformation at both the sender's and receiver's ends. For example, in case of encryption, the secret information can be a key used for encrypting and decrypting the message.
 Secure message: This refers to the message obtained after applying a transformation. It contains the secret code that helps the receiver retrieve the original message.
Secure message: This refers to the message obtained after applying a transformation. It contains the secret code that helps the receiver retrieve the original message.
 Logical information channel: This refers to the transmission route from a source to a destination, connected via a network. The route is established by the supportive use of communicating protocols by both parties.
Logical information channel: This refers to the transmission route from a source to a destination, connected via a network. The route is established by the supportive use of communicating protocols by both parties.
 Trusted third party: This is an entity that may either be responsible for transmitting the secret information to the two trusted parties while protecting it from an attacker, or may be responsible for settling disputes regarding the authenticity of a message transmission between two parties.
Trusted third party: This is an entity that may either be responsible for transmitting the secret information to the two trusted parties while protecting it from an attacker, or may be responsible for settling disputes regarding the authenticity of a message transmission between two parties.

Figure 1.3 Model of Network Security
According to this model, there are four basic tasks that are required for designing any security service. These tasks are:
 Designing an algorithm to perform security-related transformation. The algorithm should be designed in such a way that an intruder cannot defeat its purpose.
Designing an algorithm to perform security-related transformation. The algorithm should be designed in such a way that an intruder cannot defeat its purpose.
 Generating the secret information to be used with the algorithm.
Generating the secret information to be used with the algorithm.
 Developing some techniques for the sharing and distribution of the secret information.
Developing some techniques for the sharing and distribution of the secret information.
 Selecting a protocol to be used by the two parties. This protocol makes use of the secret information and security algorithm to achieve a specific security service.
Selecting a protocol to be used by the two parties. This protocol makes use of the secret information and security algorithm to achieve a specific security service.
This model secures the information in such a way that an intruder on the network cannot access it. However, within the organization, the information's security can still be threatened by unauthorized access, or by software attacks such as viruses and worms. To protect information from such threats, some security mechanisms should be implemented, as follows:
 Password-based login: This is used to deny access to all unauthorized users.
Password-based login: This is used to deny access to all unauthorized users.
 Screening login: This is used to detect and remove viruses, worms and other similar attacks.
Screening login: This is used to detect and remove viruses, worms and other similar attacks.
8. Categorize different types of network security attacks on the basis of security goals.
Ans.: As we know, for secured communication, some goals such as confidentiality, integrity and availability have been defined. However, these goals can be threatened by various security attacks. The categorization of attacks on the basis of security goals is shown in Figure 1.4.
 Attacks to integrity: The attacks that threaten the integrity of the data are masquerading, modification, repudiation and replay.
Attacks to integrity: The attacks that threaten the integrity of the data are masquerading, modification, repudiation and replay.
 Masquerading: Refer Question 4 in this chapter.
Masquerading: Refer Question 4 in this chapter.
 Modification: Refer Question 4 in this chapter.
Modification: Refer Question 4 in this chapter.
 Repudiation: Repudiation occurs when the message sender denies that the message was sent by him/her, or when the message receiver denies that the message was received by him/her.
Repudiation: Repudiation occurs when the message sender denies that the message was sent by him/her, or when the message receiver denies that the message was received by him/her.
 Replay: Refer Question 4 in this chapter.
Replay: Refer Question 4 in this chapter.

Figure 1.4 Categorization of Attacks in Relation to Security Goals
 Attacks to confidentiality: The attacks that threaten the confidentiality of data are snooping and traffic analysis.
Attacks to confidentiality: The attacks that threaten the confidentiality of data are snooping and traffic analysis.
 Snooping: Snooping refers to interception or unauthorized access of data. For example, an unauthorized entity may access a file containing confidential information during its transmission over a network and use that information for its benefits. Snooping can be prevented with the help of various encryption techniques, by making the data non-understandable to the unauthorized entity.
Snooping: Snooping refers to interception or unauthorized access of data. For example, an unauthorized entity may access a file containing confidential information during its transmission over a network and use that information for its benefits. Snooping can be prevented with the help of various encryption techniques, by making the data non-understandable to the unauthorized entity.
 Traffic analysis: Refer Question 4 in this chapter.
Traffic analysis: Refer Question 4 in this chapter.
 Attacks to availability: The attack that threatens availability is called denial of service (DoS).
Attacks to availability: The attack that threatens availability is called denial of service (DoS).
 Denial of service (DoS): Refer Question 4 in this chapter.
Denial of service (DoS): Refer Question 4 in this chapter.
Multiple-choice Questions
1. __________ ensures that a message was received by the receiver from the actual sender and not from an attacker.
(a) Authentication
(b) Authorization
(c) Integration
(d) None of these
2. Which of the following services is not an authentication service?
(a) Peer entity authentication
(b) Data origin authentication
(c) Data destination authentication
(d) None of these
3. Which of the following is a passive attack?
(a) Masquerade
(b) Replay
(c) Denial of service (DoS)
(d) Traffic analysis
4. Which of the following attacks is not a threat to the integrity of data?
(a) Masquerade
(b) Modification
(c) Repudiation
(d) Snooping
5. Which RFC document includes a definition of security service?
(a) RFC 2828
(b) RFC 2401
(c) RFC 3310
(d) RFC 6600
Answers
1. (a)
2. (c)
3. (d)
4. (d)
5. (a)
1. Explain the term cryptography in brief.
Ans.: Cryptography is a means for implementing some security mechanisms. The term cryptography is derived from the Greek word kryptos, which means “secret writing”. In simple terms, cryptography is the process of altering messages in a way that their meaning is hidden from adversaries who might intercept them. It allows the sender to disguise a message to prevent it from being read or altered by an intruder, and it also enables the receiver to recover the original message from the disguised one.
In data and telecommunications, cryptography is an essential technique required for communicating over any untrusted medium, which includes any network, such as the Internet. By using cryptographic techniques, the sender can first encrypt a message and then transmit it through the network. The receiver on the other hand can decrypt the message and recover its original contents.
Cryptography relies upon two basic components: an algorithm (or cryptographic methodology) and a key. Algorithms are the complex mathematical formulae and keys are the strings of bits. For two parties to communicate over a network (the Internet), they must use the same algorithm (or algorithms that are designed to work together). In some cases, they must also use the same key.
2. Define the following terms:
(a) Plaintext
(b) Ciphertext
(c) Encryption
(d) Decryption
(e) Cipher
(f) Key
Ans.: These terms can be defined as follows:
(a) Plaintext: It refers to the original unencrypted message that the sender wishes to send.
(b) Ciphertext: It refers to the encrypted message that is received by the receiver.
(c) Encryption: It is the process of encrypting the plaintext so that the ciphertext can be produced. Plaintext is transformed into ciphertext using the encryption algorithm.
(d) Decryption: It is the reverse of the encryption process. In this process, the ciphertext is converted back to the plaintext using a decryption algorithm.
(e) Ciphers: The encryption and decryption algorithms are together known as ciphers. Ciphers need not necessarily be unique for each communicating pair; rather a single cipher can be used for communication between multiple pairs of senders and receivers.
(f) Key: A key is usually a number or a set of numbers on which the cipher operates. Encryption and decryption algorithms make use of a key to encrypt or decrypt messages, respectively. At the sender's end, the encryption algorithm and encryption key are required to convert the plaintext into ciphertext. At the receiver's end, a decryption algorithm uses the decryption key to convert ciphertext back into the plaintext. The longer the key is, the harder it is for an attacker to decrypt the message.
3. Explain symmetric-key and asymmetric-key encipherment.
Ans.: Traditionally, cryptography involves the use of the same key for encrypting or decrypting the messages (symmetric-key encipherment). However, modern cryptography involves the use of different keys for encryption and decryption (asymmetric-key encipherment).
Symmetric-key Encipherment
The symmetric-key encipherment, sometimes also called secret-key encipherment or secret-key cryptography, uses a single shared key (secret key) for both encryption and decryption of data. Thus, it is obvious that the key must be known to both the sender and the receiver. As shown in Figure 2.1, the sender uses the shared key and the encryption algorithm to transform the plaintext into ciphertext. The ciphertext is then sent to the receiver via a communication network. The receiver applies the same key and the decryption algorithm to decrypt the ciphertext and to recover the plaintext. Some examples of symmetric-key algorithms include Data Encryption Standard (DES), double DES, triple DES, and Advanced Encryption Standard (AES).

Figure 2.1 Message exchange using secret key
The main problem in secret-key cryptography is getting the sender and receiver to agree on the secret key without anyone else finding it out. If the key is compromised, the security offered by secret-key cryptography is severely reduced or eliminated. Secret-key cryptography assumes that the parties who share a key rely upon each other not to disclose the key and protect it against modification. If they are in separate physical locations, they must trust a medium such as the courier or a phone system to prevent the disclosure of the secret key. Anyone who overhears or intercepts the key in transit can later read, modify, and forge all messages encrypted or authenticated using that key.
Asymmetric-key Encipherment
The asymmetric-key encipherment, sometimes also called public-key encipherment or public-key cryptography, was introduced by Diffie and Hellman in 1976 to overcome the problem found in symmetric-key cryptography. It involves the use of two different keys for encryption and decryption. These two keys are referred to as the public key (used for encryption) and the private key (used for decryption). Each authorized user has a pair of public and private keys. The public key of each user is known to everyone, whereas the private key is known to its owner only.
Now, suppose that a user A wants to transfer some information to user B securely. The user A encrypts the data by using the public key of B and sends the encrypted message to B. On receiving the encrypted message, B decrypts it by using his/her private key. Since decryption process requires a private key of user B, which is only known to B, the information is transferred securely. Figure 2.2 illustrates the whole process. RSA is a well-known example of asymmetric-key algorithm.

Figure 2.2 Message exchange using public key
The main advantage of public-key cryptography is that the need for the sender and the receiver to share the secret key is eliminated and all communication involves only public keys. Thus, the private key is never transmitted or shared. Anyone can send a confidential message using a public key, but the message can only be decrypted with a private key, which is in the sole possession of the intended recipient.
4. Differentiate between symmetric-key and asymmetric-key cryptography.
Ans.: Some differences between symmetric-key and asymmetric-key cryptography are listed in Table 2.1.
| Symmetric-key cryptography | Asymmetric-key cryptography |
|---|---|
| 1. It uses a single key for both encryption and decryption of data. | 1. It uses two different keys—public key for encryption and private key for decryption. |
| 2. Both the communicating parties share the same algorithm and the key. | 2. Both the communicating parties should have at least one of the matched pair of keys. |
| 3. The processes of encryption and decryption are very fast. | 3. The encryption and decryption processes are slower as compared to symmetric-key cryptography. |
| 4. Key distribution is a big problem. | 4. Key distribution is not a problem. |
| 5. The size of encrypted text is usually same or less than the original text. | 5. The size of encrypted text is usually more than the size of the original text. |
| 6. It can only be used for confidentiality, that is, only for encryption and decryption of data. | 6. It can be used for confidentiality of data as well as for integrity and non-repudiation checks (that is, for digital signatures). |
| 7. DES and AES are the commonly used symmetric-key algorithms. | 7. The most commonly used asymmetric-key algorithm is RSA. |
5. What is cryptanalysis? Also, discuss different cryptanalysis attacks.
Ans.: Cryptanalysis is the art and science of breaking the encrypted codes that are created by applying some cryptographic algorithms. The person who performs cryptanalysis is known as a cryptanalyst. A cryptanalysis attack is made by a cryptanalyst to obtain the plaintext or the key that was used to encrypt a message. Depending on the information that the cryptanalyst has, cryptanalysis attacks can be classified under the following categories:
 Ciphertext-only attack: In this type of attack, the cryptanalyst has a part of the ciphertext available and using this information, he/she tries to find out the corresponding key and decipher the plaintext. This attack is based on the assumption that the cryptanalyst knows the algorithm that has been used to encrypt the message and can easily intercept the ciphertext. These types of attacks are very common because the attacker just needs to have the knowledge of the ciphertext. However, we can prevent a cryptanalyst from decrypting the ciphertext by using a strong cipher, which makes it very difficult for the cryptanalyst to decrypt the message. Some common methods that can be used to determine the key or break the ciphers in ciphertext-only attacks include brute-force, statistical, and pattern attacks. Figure 2.3 depicts the process of ciphertext-only attack where
Ciphertext-only attack: In this type of attack, the cryptanalyst has a part of the ciphertext available and using this information, he/she tries to find out the corresponding key and decipher the plaintext. This attack is based on the assumption that the cryptanalyst knows the algorithm that has been used to encrypt the message and can easily intercept the ciphertext. These types of attacks are very common because the attacker just needs to have the knowledge of the ciphertext. However, we can prevent a cryptanalyst from decrypting the ciphertext by using a strong cipher, which makes it very difficult for the cryptanalyst to decrypt the message. Some common methods that can be used to determine the key or break the ciphers in ciphertext-only attacks include brute-force, statistical, and pattern attacks. Figure 2.3 depicts the process of ciphertext-only attack where A and B are the communicating parties and C is the cryptanalyst (attacker).

Figure 2.3 Ciphertext-only attack
 Known-plaintext attack: In this type of attack, the attacker already has some plaintext-ciphertext pairs in addition to the ciphertext that he/she wishes to break. Figure 2.4 depicts the process of known-plaintext attack by
Known-plaintext attack: In this type of attack, the attacker already has some plaintext-ciphertext pairs in addition to the ciphertext that he/she wishes to break. Figure 2.4 depicts the process of known-plaintext attack by C during communication between A and B. Suppose that A sent a secret message to B; however, later, A made the contents of that message public. Further, assume that the attacker C has kept both ciphertext and plaintext (which is now public). Thus, C tries to obtain a relationship between these pairs to find the key used to encrypt the plaintext so that he/she can break the next block of ciphertext from A to B; provided that A uses the same key to encrypt the message as that for the previous message. This type of attack is easy to implement because the attacker has more information to analyze the ciphertext. However, this attack happens rarely because it is more likely that the sender changes the key for every transmission of message, or that the message contents are not made public.

Figure 2.4 Known-plaintext attack
 Chosen-plaintext attack: This attack is similar to the known-plaintext attack with the only difference being that in this attack, the attacker
Chosen-plaintext attack: This attack is similar to the known-plaintext attack with the only difference being that in this attack, the attacker C himself/herself chooses the plaintext–ciphertext pairs. However, it is possible only if C gets access to A's computer by some means. The attacker C can then select some plaintext from A's computer that helps him/her to intercept the created ciphertext. This process is shown in Figure 2.5.

Figure 2.5 Chosen-plaintext attack
 Chosen-ciphertext attack: A chosen-ciphertext attack is similar to a chosen-plaintext attack. The only difference between the two being that in chosen-ciphertext attack, the attacker
Chosen-ciphertext attack: A chosen-ciphertext attack is similar to a chosen-plaintext attack. The only difference between the two being that in chosen-ciphertext attack, the attacker C chooses some ciphertext and then decrypts it to make a ciphertext-plaintext pair. This is possible if C gets access to B's computer. This process is shown in Figure 2.6.

Figure 2.6 Chosen-ciphertext attack
 Chosen-text attack: A chosen-text attack is a combination of chosen-plaintext and chosen-ciphertext attack.
Chosen-text attack: A chosen-text attack is a combination of chosen-plaintext and chosen-ciphertext attack.
6. What is key management? Also, explain the functions of key management.
Ans.: Though cryptography enables maintaining the secrecy of a message, it works only as long as the keys used for encryption and decryption are kept secret. Thus, the secrecy of cryptographic keys is central to the encryption mechanism, and it is achieved through key management. Key management refers to the collection of processes used for the generation, storage, installation, transcription, recording, change, disposition, and control of keys that are used in cryptography. It is essential to the secure ongoing operation of any cryptosystem. The various functions of key management are as follows:
 Generation: This process involves the selection of a key that is to be used for encrypting and decrypting the messages. The key may be generated for the sender, receiver, or an application. It must be long enough to be predicted by a cryptanalyst. Moreover, it must be chosen randomly and its information must not be leaked during the whole process.
Generation: This process involves the selection of a key that is to be used for encrypting and decrypting the messages. The key may be generated for the sender, receiver, or an application. It must be long enough to be predicted by a cryptanalyst. Moreover, it must be chosen randomly and its information must not be leaked during the whole process.
 Distribution: This process involves all the efforts made in carrying the key from the point where it is generated to the point where it is to be used. Distribution is more difficult in symmetric-key cryptography where the key has to be transmitted via a secure channel.
Distribution: This process involves all the efforts made in carrying the key from the point where it is generated to the point where it is to be used. Distribution is more difficult in symmetric-key cryptography where the key has to be transmitted via a secure channel.
 Installation: This process involves getting the key into the storage of the device or the process that needs to use this key. Note that if this process involves manual operations, then it might result in leakage of key information.
Installation: This process involves getting the key into the storage of the device or the process that needs to use this key. Note that if this process involves manual operations, then it might result in leakage of key information.
 Storage: This process involves maintaining the confidentiality of stored or installed keys while preserving the integrity of the storage mechanism. The mechanism may be designed in such a way that once the key is installed, no one from the outside the encryption machine can intercept it. Alternatively, for an effective implementation, the key may be stored in an encrypted form such that the knowledge of the stored key does not disclose the behaviour of the device in which the key is being used.
Storage: This process involves maintaining the confidentiality of stored or installed keys while preserving the integrity of the storage mechanism. The mechanism may be designed in such a way that once the key is installed, no one from the outside the encryption machine can intercept it. Alternatively, for an effective implementation, the key may be stored in an encrypted form such that the knowledge of the stored key does not disclose the behaviour of the device in which the key is being used.
 Change: This process involves ending with the use of one key and starting the use of another. The longer the key is in use and more is the traffic encrypted by it, higher are the chances that it will be intercepted. Therefore, the key must be changed after some time. It may noted that the information about the key is prone to leakage during the key change time.
Change: This process involves ending with the use of one key and starting the use of another. The longer the key is in use and more is the traffic encrypted by it, higher are the chances that it will be intercepted. Therefore, the key must be changed after some time. It may noted that the information about the key is prone to leakage during the key change time.
7. Describe the general rules for maintaining an effective key management system?
Ans.: An effective key management system should follow certain basic rules that are defi ned as follows:
 The secret key must be stored and transmitted in a secure manner because disclosure of the secret key makes the data unsecured.
The secret key must be stored and transmitted in a secure manner because disclosure of the secret key makes the data unsecured.
 The longer the same key is in use, the easier it becomes to crack the key. Thus, the key must be changed from time to time.
The longer the same key is in use, the easier it becomes to crack the key. Thus, the key must be changed from time to time.
 The key must be generated randomly, so that it is hard for any attacker to guess it. The higher the randomness of the key is, higher will be the quality of the key, making it progressively more difficult to guess it.
The key must be generated randomly, so that it is hard for any attacker to guess it. The higher the randomness of the key is, higher will be the quality of the key, making it progressively more difficult to guess it.
 If the length of the key is short, its lifetime must also be short. That is, a short key must not be used for a longer period of time.
If the length of the key is short, its lifetime must also be short. That is, a short key must not be used for a longer period of time.
 The key must be destroyed properly after its use.
The key must be destroyed properly after its use.
8. Briefly discuss the concept of steganography.
Ans.: Steganography, like cryptography, is a technique to implement security mechanisms. The term steganography comes from the Greek word steganos, which means “concealed writing”. Steganography is the technique of writing a message in such a way that apart from the sender and the receiver, no one will suspect the existence of the message. It enables the sender to hide a message inside another message. Although both steganography and cryptography are security mechanisms intended to protect the messages from attackers, but still they differ from each other. Where cryptography conceals the contents of a message by enciphering, steganography conceals the message itself by covering it with something.
Some of the traditional techniques of steganography include:
 Marking selected letters of a printed document with a pencil such that the marks are visible only when the document is exposed at a specific angle to bright light.
Marking selected letters of a printed document with a pencil such that the marks are visible only when the document is exposed at a specific angle to bright light.
 Use of some invisible ink (such as onion juice, lemon juice, or some ammonia salt) to write a secret message such that the contents of a message are not visible until heated or some other chemical is applied.
Use of some invisible ink (such as onion juice, lemon juice, or some ammonia salt) to write a secret message such that the contents of a message are not visible until heated or some other chemical is applied.
 Use of microdots or pin punchers on selected letters such that these dots are not visible until the paper is exposed in front of a light.
Use of microdots or pin punchers on selected letters such that these dots are not visible until the paper is exposed in front of a light.
Some modern techniques of steganography include hiding of a secret message within an image, audio or video file by inserting secret binary message information during the digitization process. Although the digitization process may result in an extra overhead to hide a relatively small message, it is more effective when used along with cryptography.
9. Explain Euclidean algorithm for finding the greatest common divisor.
Ans.: The Euclidean algorithm (also called Euclid's algorithm) is an efficient algorithm for finding the greatest common divisor (GCD) of two positive integers. This algorithm was invented by the Greek mathematician Euclid and is hence named after him. Given two positive integers x and y, then another positive number (say, a) is called the gcd of x and y if and only if the following conditions are satisfied:
(i) a divides both x and y.
(ii) Any other common divisor of x and y also divides a.
In other words, gcd(x,y)=a if a is the largest integer that divides both x and y.
Euclidean's algorithm computes the gcd of two positive integers, x and y, based on the following facts:
(i) gcd(x,0)=x, that is, if the second integer is zero, then the gcd is the first integer.
(ii) gcd(x,y)=gcd(y,r), where r is the remainder obtained on dividing x by y.
Algorithm
The following are the steps to find the gcd of two positive integers x and y, where x>y>0 using Euclidean's algorithm, are as follows:
1. a:=x
2. b:=y
3. while (b>0)
{
q:=a/b
r:=a-q*b
a:=b
b:=r
}
4. gcd(x,y):=a
In this algorithm, we have used two variables a and b to hold the remainders produced during the reduction process. To start with, variables a and b are initialized with x and y, respectively. During each step in the reduction process, we calculate the remainder of a divided by b and then store it into the variable r. Then, a and b are replaced with b and r, respectively. This process is continued until the value of b becomes zero. Eventually, we get the gcd(x, y)as a.
10. Write a short note on modular arithmetic.
Ans.: In mathematics, to perform a division operation, we need two inputs, a divisor (say, m) and a dividend (say, x). After performing the operation we get two outputs, a quotient (say, q) and a remainder (say, r). That is, the division relationship can be expressed as follows:
x=m*q+r
However, in modular arithmetic, we are interested in only one output, that is, the remainder, while the other output (that is, the quotient) is not considered. Thus, in this case, the division operation can be expressed as a binary operator having two inputs, the integers x and m and only one output r. This binary operator is referred to as the modulo operator (written as mod). The input m (divisor) to the modulo operator is referred to as the modulus, while the output r is referred to as the residue. Thus, we can say that:
x mod m=r
where x is an integer from the set of integers Z={…,-3,-2,-1,0,1,2,3,…} and the modulus (m) and residue (r) are the positive integers. In case the value of x is negative, the value of r also comes out negative. Thus, to make it non-negative, the modulus m is added to r.
11. Explain the following with reference to modular arithmetic:
(a) Set of residues
(b) Congruence
(c) Additive and multiplicative inverse
Ans.: (a) Set of residues: Consider a modulo operation x mod m=r, where x is an integer from a set of integers Z while m and r are positive integers. The result of this operation is always an integer less than m. That is, the value of r lies between 0 and m-1. Thus, it can be said that the modulo operation results in a set containing elements from 0 to m-1. In modular arithmetic, this set is called the set of least residues modulo m (denoted as Zm) or simply the set of residues. There can be infinite possible instances of Zm, one for each value of m. For example, Z11 can have 11 values {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, Z4 can have four values {0, 1, 2, 3}, and so on.
Modular arithmetic allows three binary operations: addition, subtraction, and multiplication to be applied on the elements of Zm. After applying each operation, the result obtained may need to be mapped to Zm with the help of the modulo operator. To understand, consider three elements x, y, and z such that both x and y belong to Z (or Zm) and z belongs to Zm. Then the binary operations in Zm can be expressed as (also see Figure 2.7):
(x+y) mod m=z
(x-y) mod m=z
(x*y) mod m=z

Figure 2.7 Binary operations in Zm
(b) Congruence: There is always a many-to-one relationship between Z and Zm. That is, many elements of the set Z can map to a single element of Zm. For example, modulo operations 3 mod 10, 13 mod 10, and 23 mod 10 result in the same value (equal to 3). Thus, these numbers (3, 13, and 23) are referred to as congruent mod 10 in modular arithmetic. To represent the congruence relationship between two integers, the congruence operator represented by the ‘≡’ symbol is used. For example, we can write that 3 ≡ 13 (mod 10), 13 ≡ 23 (mod 10), and 3 ≡ 23 (mod 10).
(c) Additive and multiplicative inverse: While working with modular arithmetic, we often need to determine the inverse of an element with respect to some operation. Two commonly required inverses are additive and multiplicative inverses. The former is the inverse with respect to the addition operation, while the latter is the inverse with respect to the multiplication operation.
Each element in modular arithmetic has only one additive inverse, which is always unique; sometimes, the additive inverse of an element is the element itself. Let x and y be two elements of the set Zm. Now, x is said to be the additive inverse of y and vice versa if:
x+y≡0 (mod m)
Simply put, the additive inverse of any element, say x in Zm is equal to m-x. For example, the additive inverse of 11 in Z15={0,1,2,…,13,14} is 4 (15-11).
On the other hand, an element may or may not have a multiplicative inverse. Let x and y be two elements of the set Zm. Now, x is said to the multiplicative inverse of y and vice versa if:
x*y≡1 (mod m)
For example, the multiplicative inverse of 7 in Z15={0,1,2,…,13,14} is 13, as 7*13≡1 (mod 15).
The simple method to determine whether or not a number (x) in Zm has a multiplicative inverse is to compute the GCD of x and m. If gcd(x,m)comes out to be one, x has a multiplicative inverse; otherwise, the multiplicative inverse for x in Zm does not exist. For example, there does not exist a multiplicative inverse for number 5 in Z15 because gcd(5,15)≠ 1. Notice that if gcd(x,m)=1, x and m are said to be relatively prime.
12. Describe the extended Euclidean algorithm to find the multiplicative inverse.
Ans.: The extended Euclidean algorithm is an extension to the Euclidean algorithm. Besides finding the gcd of two positive integers x and y, it simultaneously finds the multiplicative inverses a and b such that:
m*x+n*y=gcd(x,y)
where m is the multiplicative inverse of x mod y and n is the multiplicative inverse of y mod x.
Algorithm
The following are the steps involved in the extended Euclidean algorithm to find the gcd of two positive integers along with the multiplicative inverses are as follows:
1. a:=x
2. b:=y
3. c:=1
4. d:=0
5. e:=0
6. f:=1
7. while (b>0)
{
q:=a/b
r:=a-q*b
a:=b
b:=r
m:=c-q*d
c:=d
d:=m
n:=e-q*f
e:=f
f:=n
}
8. gcd(x,y):=a
9. m:=c
10. n:=e
Similar to the Euclidean algorithm, the extended Euclidean algorithm also uses the reduction process to find the gcd and multiplicative inverses. It uses three sets of variables, (a,b), (c,d), and (e,f) and during each step of the reduction process, three sets of calculations are made, one per each set of variables. To start with, the variables a, b, c, d, e, and f are initialized with x, y, 1, 0, 0, and 1, respectively. In the while loop, variables q and r are used to hold the quotient and the remainder of a divided by b, respectively. Then, variables a and b are updated in a similar manner as in the Euclidean algorithm. The set of variables (c,d) and (e,f) are also updated on the basis of q's value. This process continues until the value of b becomes zero. Finally, we obtain the gcd(x,y) as a as well as the values of m and n.
13. What is an algebraic structure? Also, explain group, ring, and field.
Ans.: An algebraic structure refers to the combination of a set of integers and the operations that are defined on the elements of the set. The commonly used algebraic structures are as follows:
Group
A group (G), denoted as G=<{…},•>, is a set of elements along with a binary operation “•” performed on each ordered pair (x,y) of elements of G such that x•y satisfies the following four properties:
(a) Closure: If both x and y belong to the same group G, then x•y also is in G. That is, if x and y are the elements of the same group, then the result of a binary operation on these elements is another element of that group.
(b) Associativity: If x, y, and z belong to the same group G, then (x•y)•z=x•(y•z). That is, the order of operation does not affect the result.
(c) Existence of identity: For each element x in G, there always exists an identity element e within the same group such that x•e=e•x = x.
(d) Existence of inverse: For each element x in G, there always exists an inverse element x′ within the same group such that x•x′=x′•x=e.
A group that satisfies all the four properties of a group and an additional property called commutativity is said to be an abelian group, also called commutative group. The commutative property states that for all x and y belonging to G, x•y = y•x.
A group that contains a finite number of elements is referred to as a finite group, whereas a group that is not finite is called an infinite group. For example, a group G1=<{1,3,5,7,9},+> is a finite group while a group G2=<Zn,+> where Zn is a set of integers, is an infinite group. The number of elements in a group indicates the order of the group. For example, the order of group G1 is five while the order of group G2 is infinite.
Ring
A ring (R), denoted as R=<{…},•, , is a set of elements with two binary operations, “ >
>•” and “

R is an abelian group with respect to the first operation (•). In other words, R satisfies the closure, associativity, commutativity, existence of identity, and existence of inverse properties with respect to the “•” operation.

R satisfies the closure and associativity properties with respect to the second operation ( ). In addition, the second operation (
). In addition, the second operation ( ) must be distributed over the first operation (
) must be distributed over the first operation (•). The distributivity of the second operation over the first means that if x, b, and c are the elements of ring R, then x (
y•z) = (x )  y
y• (x ) and ( z
zx•y)  z
zx )  z
z• (y ). z
z
A ring is said to be a commutative ring if it satisfies all the properties of a ring plus if the second operation ( ) also satisfies the commutative property, that is for all
) also satisfies the commutative property, that is for all x and y belonging to the ring R, x  y=y
y=y  x
x
Field
A field (F), denoted as F=<{…},•,>, is a set of elements with two binary operations, “•” and “
 ”, such that
”, such that F is a commutative ring where the second operation ( ) satisfies all the five properties defined for the first operation (
) satisfies all the five properties defined for the first operation (•) except that there is no inverse for the identity element of the first operation with respect to the second operation.
14. Explain each finite field of the form GF(pn).
Ans.: A field with a finite number of elements is called a finite field. The finite fields are the most important and most frequently used in cryptography for performing modular arithmetic operations. The concept and theory of finite fields was given by Galois, according to which if a field is finite, then it contains pn number of elements, where p is a prime number and n is a positive integer. Thus, the finite fields are usually known as Galois field and is denoted by GF(pn).
A finite field with n=1 is called the GF(p) field. This field is in fact the set Zp={0,1,…,p-1}, in which two arithmetic operations, addition and multiplication, can be applied. Each element of this set has an additive and multiplicative inverse except zero, which has no multiplicative inverse.
As we know, positive integers are stored in computers in the form of n-bit words, where the value of n can be 8, 16, 32, and so on. This implies that the range of integers that can be stored is 0 to 2n-1 and the modulus is 2n. Now, using the GF(p) finite field with the set Zp, where p is the largest prime number less than 2n-1, would be inefficient as the integers ranging from p to 2n-1 will not be used. To overcome this inefficiency of the GF(p) field, the GF(2n) field is used. This field uses a set of 2n elements, and each element is an n-bit word.
15. Find out the result of the following operations:
(a) 140 mod 10
(b) -73 mod 13
(c) 0 mod 7
Ans.: (a) When 140 is divided by 10, we get the remainder r=0. This means that 140 mod 10=0.
(b) When -73 is divided by 13, we get the remainder r=-8. To make r non-negative, we need to add modulus (13) to r. That is, r =-8+13=5. This means that -73 mod 13=5.
(c) When 0 is divided by 7, we get the remainder r =7. This means that 0 mod 7 = 7.
16. Find the GCD of 2740 and 1760 using the Euclidean algorithm.
Ans.: Using the Euclidean algorithm as explained in Question 9, we have x = 2740 and y = 1760.
Now, initializing a = x and b = y, we get a = 2740 and b = 1760. As b > 0, we move to the first iteration of the while loop.
Algorithm
First iteration
q=2740/1760=1
r=2740-1*1760=980
a=1760
b=980
As 980 > 0, we move to the next iteration.
Second iteration
q=1760/980=1
r=1760-1*980=780
a=980
b=780
As 780 > 0, we move to the next iteration.
Third iteration
q=980/780=1
r=980-1*780=200
a=780
b=200
As 200 > 0, we move to the next iteration.
Fourth iteration
q=780/200=3
r=780-3*200=180
a=200
b=180
As 180 > 0, we move to the next iteration.
Fifth iteration
q=200/180=1
r=200-1*180=20
a=180
b=20
As 20 > 0, we move to the next iteration.
Sixth iteration
q=180/20=9
r=180-9*20=0
a=20
b=0
As the value of b has become zero, the while loop terminates.
Thus, gcd(x, y)=a

gcd(2740, 1760)=20
17. Find the greatest common divisor of 400 and 60 using the extended Euclidean algorithm. Also, find the values of m and n.
Ans.: Using the extended Euclidean algorithm as explained in Question 12, we have x = 400 and y = 60. Now, initializing a = x and b = y, we get a = 400 and b = 60. We also know that c = 1, d = 0, e = 0, and f = 1.
As b>0, we move to the first iteration of the while loop.
First iteration
q = 400/60=6
r = 400-6*60=40
a = 60
b = 40
m = 1-6*0=1
c = 0
d = 1
n = 0-6*1=-6
e = 1
f = -6
As 40 > 0, we move to the next iteration.
Second iteration
q = 60/40=1
r = 60-1*40=20
a = 40
b=20
m = 0-1*1=-1
c = 1
d = -1
n = 1-1*(-6)=7
e = -6
f = 7
As 20 > 0, we move to the next iteration.
Third iteration
q = 40/20=2
r = 40-2*20=0
a = 20
b = 0
m = 1-2*(-1)=3
c = -1
d = 3
n = (-6) -2*7=-20
e = 7
f = -20
As the value of b has become zero, the while loop terminates.
Now, gcd(x, y)=a, m = c, and n = e. Thus, gcd(400, 60)=20, m = -1, and n = 7.
Multiple-choice Questions
1. The conversion of ciphertext into plaintext is known as __________.
(a) Encryption
(b) Decryption
(c) Cryptography
(d) Cryptanalyst
2. Which of the following is a component of cryptography?
(a) Ciphertext
(b) Ciphers
(c) Key
(d) All of these
3. Which of the following is needed to implement a chosen-plaintext attack?
(a) The attacker must have knowledge of the ciphertext.
(b) The attacker must have access to the receiver's computer.
(c) The attacker must have access to the sender's computer.
(d) Both (a) and (b)
4. Which of the following is needed to implement a chosen-ciphertext attack?
(a) The attacker must have knowledge of the ciphertext.
(b) The attacker must have access to the receiver's computer.
(c) The attacker must have access to the sender's computer.
(d) Both (a) and (b)
5. What is a chosen-text attack?
(a) It is a combination of known-plaintext attack and chosen-ciphertext attack.
(b) It is a combination of chosen-plaintext attack and known-ciphertext attack.
(c) It is a combination of known-plaintext attack and known-ciphertext attack.
(d) It is a combination of chosen-plaintext attack and chosen-ciphertext attack.
6. Which of the following are the functions of key management?
(a) Key generation, distribution, and installation
(b) Key storage, key change, and key control
(c) Both (a) and (b)
(d) None of these
7. Which of the following is true in the context of steganography?
(a) It conceals the existence of the message.
(b) It conceals the contents of the message.
(c) It involves less overhead than cryptography.
(d) Both (a) and (b)
8. In public-key cryptography, __________ key is used for encryption.
(a) Public
(b) Private
(c) Both (a) and (b)
(d) Shared
9. The multiplicative inverse of 13 in Z15 is __________.
(a) Five
(b) Seven
(c) Nine
(d) Eight
10. Which of the following properties designates a group as an abelian group?
(a) Closure
(b) Associativity
(c) Distributivity
(d) Commutativity
Answers
1. (b)
2. (d)
3. (c)
4. (d)
5. (d)
6. (c)
7. (a)
8. (a)
9. (b)
10. (d)
1. Define a symmetric-key cipher.
Ans.: A cipher (a combination of encryption and decryption algorithms) that uses the same key for both encryption and decryption is referred to as a symmetric-key cipher.
2. Explain the symmetric cipher model.
Or
Explain the conventional encryption model.
Ans.: A symmetric cipher model (also referred to as a conventional encryption model) consists of various components (see Figure 3.1), which are described as follows:

Figure 3.1 Symmetric Cipher Model
(a) Plaintext: This refers to the original message that the sender wishes to send securely. It is an input to the encryption algorithm.
(b) Encryption algorithm: This algorithm applies various substitutions and transpositions on the plaintext, with the help of a secret key, to transform it into an unintelligible form. The encryption algorithm is used at the sender's end.
(c) Ciphertext: This refers to the coded (scrambled) message that is produced by the encryption algorithm. The ciphertext is sent to the receiver through a communication channel.
(d) Decryption algorithm: This is the opposite of an encryption algorithm. It is used at the receiver's end to convert ciphertext back into plaintext (original message). The encryption and decryption algorithms are together known as ciphers.
(e) Secret (shared) key: This usually refers to a number or a set of numbers on which the cipher operates. Both encryption and decryption algorithms use the same key (shared between the sender and receiver) to encrypt or decrypt the messages, respectively.
3. What are the issues in a conventional encryption model?
Ans.: Though conventional encryption is fast, efficient and excellent for large data transmissions such as file transfers, it suffers from certain limitations, which are as follows:
 As the sender and receiver share a single key, the key must be sent via a secure channel. However, if such a secure channel already exists, the question then arises as to why encryption was required in the first place.
As the sender and receiver share a single key, the key must be sent via a secure channel. However, if such a secure channel already exists, the question then arises as to why encryption was required in the first place.
 Exchanging the secret key using unsecure channels such as telephone lines, which are prone to eavesdropping, may violate the confidentiality of the key.
Exchanging the secret key using unsecure channels such as telephone lines, which are prone to eavesdropping, may violate the confidentiality of the key.
 There are some organizations that deal with thousands or million's of clients on a daily basis. In such organizations, it is extremely difficult to assign a unique key to each client.
There are some organizations that deal with thousands or million's of clients on a daily basis. In such organizations, it is extremely difficult to assign a unique key to each client.
4. What are the different categories of classical encryption techniques?
Ans.: The classical encryption techniques, also referred to as traditional symmetric-key ciphers, are divided into two categories: substitution ciphers and transposition ciphers.
 Substitution cipher: This cipher replaces a symbol (a single letter or a group of letters) of the plaintext with another symbol. For example, the letter
Substitution cipher: This cipher replaces a symbol (a single letter or a group of letters) of the plaintext with another symbol. For example, the letter A can be replaced with letter C, and letter P with letter Z. If the symbols are digits, then the digit 2 can be replaced by digit 5, and digit 3 with digit 6. Substitution ciphers are further categorized into monoalphabetic ciphers and polyalphabetic ciphers.
 Transposition cipher: In this cipher, there is no substitution of characters; rather, the location of characters in plaintext is changed to form the ciphertext. In other words, a transposition cipher reorders (transposes) the symbols in the plaintext, thereby creating the ciphertext. Thus, the order of characters in the plaintext is no longer preserved in the ciphertext. For example, a symbol at the third position in the plaintext may be placed at the eighth position in the ciphertext, or a symbol at the fifth position in the plaintext may appear at the fifteenth position in the ciphertext. Transposition ciphers are further categorized into keyless transposition ciphers and keyed transposition ciphers
Transposition cipher: In this cipher, there is no substitution of characters; rather, the location of characters in plaintext is changed to form the ciphertext. In other words, a transposition cipher reorders (transposes) the symbols in the plaintext, thereby creating the ciphertext. Thus, the order of characters in the plaintext is no longer preserved in the ciphertext. For example, a symbol at the third position in the plaintext may be placed at the eighth position in the ciphertext, or a symbol at the fifth position in the plaintext may appear at the fifteenth position in the ciphertext. Transposition ciphers are further categorized into keyless transposition ciphers and keyed transposition ciphers
5. What is a monoalphabetic cipher? Explain different techniques of monoalphabetic ciphers.
Ans.: A monoalphabetic cipher is a substitution cipher where a symbol in the plaintext has a one-to-one relationship with a symbol in the ciphertext. It means that a symbol in the plaintext is always replaced with the same symbol in the ciphertext, irrespective of its position in the plaintext. The different techniques based on monoalphabetic ciphers are as follows:
Additive cipher
This is the easiest and simplest monoalphabetic cipher, where each letter in plaintext is coded by shifting a certain number of spaces from it. For this, it uses a key that defines the number of spaces to be shifted. In this technique, each character in the plaintext is first assigned a numeric value according to its position in Z26, the set of alphabets. For example, a (or A) will be assigned 0, b (or B) will be assigned 1, c (or C) will be assigned 2, and so on. The key (say, K) used for encrypting the plaintext is also an integer in Z26.
At the sender's end, the key (K) is added to plaintext (say, P) and the result is mapped to Z26, using the modular arithmetic to form the ciphertext (say, C), as shown here.
C = (P + K) mod 26
At the receiver's end, the reverse process is followed for converting the ciphertext back to plaintext. That is, the additive inverse of key K in Z26, denoted as -K, is added to ciphertext (C) and the result is mapped to Z26 using the modular arithmetic to obtain plaintext (P), as shown here.
P = (C - K) mod 26
Figure 3.2 depicts the process of encryption and decryption in additive cipher. An example given in Question 17 illustrates the encryption and decryption processes using additive cipher.

Figure 3.2 Additive Cipher
Shift cipher
In this cipher, an encryption algorithm can be interpreted as ‘a shift by a key number of characters in the clockwise direction, that is, towards the end of the alphabet’ while a decryption algorithm can be interpreted as ‘a shift by a key number of characters in the anti-clockwise direction, that is, towards the beginning of the alphabet’. For example, for key = 5, the encryption algorithm moves five characters down in the set of alphabets (Z26), while the decryption algorithm moves five characters up the alphabet in the set of alphabets. Notice that during encryption and decryption, as the end or the beginning of the alphabet is reached, we wrap round. For the same value of the key K, both shift and additive ciphers produce the same ciphertext; thus, traditionally, additive ciphers have also been referred to as shift ciphers.
Caesar cipher
This cipher has been named after its inventor, Julius Caesar. It is simply an additive cipher with key = 3. That is, during encryption, each plaintext character is replaced with a character obtained by moving three places down in the alphabet and the reverse happens during decryption. Like shift cipher, on reaching the end or beginning of the alphabet, we wrap around. The simplicity of Caesar cipher becomes its weakness as anyone can determine the plaintext by just replacing each ciphertext character with a character obtained by moving three characters up in the alphabet.
To overcome this limitation of Caesar cipher, its enhanced version, named modified Caesar cipher, was proposed. In this cipher, a character can be replaced with any other character. However, as we know, the English alphabet has only 26 characters; hence, a character can be replaced only with one of the other 25 characters. Thus, the cipher is vulnerable to the brute-force attack, as an attacker just needs to choose one out of 25 possible characters.
Multiplicative cipher
In this cipher, the plaintext is encrypted by multiplying it with the key, while the ciphertext is decrypted by performing division on it with the key(K). Since the operations are in Z26, the result needs to mapped to Z26 using modular arithmetic. Moreover, division by key during decryption implies multiplication by the multiplicative inverse of the key in Z26 (denoted as K-1). The following are the formulae used to encrypt the plaintext (and) P decrypt the ciphertext(C), respectively.
C = (P * K) mod 26
P = (C * K-1) mod 26.
Figure 3.3 depicts the process of encryption and decryption in a multiplicative cipher. The example given in Question 17 illustrates encryption and decryption using multiplicative cipher.

Figure 3.3 Multiplicative Cipher
Affine cipher
Affine cipher is the combination of additive and multiplicative ciphers with a pair of keys. Two ciphers are applied one after another, and a separate key is used for each. The first key of the key-pair is used for the first cipher (either additive or multiplicative), while the second key is used for the other. The process of encryption and decryption in affine cipher is shown in Figure 3.4.

Figure 3.4 Affine Cipher
At the sender's side, the plaintext (P) is first encrypted using the multiplicative cipher and key K1 to obtain the temporary ciphertext (C1), as shown here:
C1 = (P * K1) mod 26
Then, the ciphertext C1 is again encrypted using the additive cipher and key K2 to obtain the final ciphertext (C), as shown here:
C = (C1 + K2) mod 26.
At the receiver's side, the algorithm first decrypts the received ciphertext (C) using the additive cipher and additive inverse of the key K2 in Z26 (denoted as -K2) to obtain a temporary plaintext (P1), as shown here:
P1 = (C - K2) mod 26
Then, the plaintext P1 is again decrypted using the multiplicative cipher and multiplicative inverse of the key K1 in Z26 (denoted as K1-1) to obtain the original plaintext(P), as shown here:
P = (P1 * K1-1) mod 26.
It should be noted that, if the second cipher is the additive cipher in encryption, then the additive inverse should be the first cipher in decryption. In the same way, if the second cipher is the multiplicative cipher in encryption, then the multiplicative inverse should be the first cipher in decryption. An example given in Question 17 illustrates the encryption and decryption processes using the affine cipher.
6. What is polyalphabetic cipher? Also, explain the different techniques of using the polyalphabetic cipher.
Ans.: In polyalphabetic cipher, the characters in the plaintext may have a one-to-many relationship with the characters in the ciphertext. This means that the same character appearing in plaintext can be replaced with a different character in the ciphertext. For example, ‘hello’ can be encrypted to ARHIF using a polyalphabetic cipher. That is, the two occurrences of the letter ‘l’ in the plaintext are replaced with different characters. Due to the one-to-many relationship between the characters of plaintext and ciphertext, the key used must indicate which of the possible characters can be used for replacing a character in the plaintext. For this, the plaintext is divided into groups of characters, and a set of keys K =(K1, K2, K3,…)is used for encrypting the groups of plaintext, such that the ith key(Ki)is used to encrypt the ith character of a plaintext group. The different techniques based on polyalphabetic ciphers are as follows:
Autokey cipher
In this cipher, the key used is a group of subkeys (K1, K2, K3,…, Kn), where each subkey is used to encrypt the corresponding character in the plaintext. That is, the first subkey is used to encrypt the first plaintext character, the second subkey is used to encrypt the second plaintext character and so on. The cipher is named so because the subkeys are generated automatically during the encryption process. The first subkey is predetermined; its value is chosen by the sender and the receiver. The second subkey is the value of the first plaintext character, the third subkey is the value of the second plaintext character and so on.
At the sender's end, a plaintext character (say, Pi) is added with the respective subkey (Ki), and the result is mapped to Z26, using modular arithmetic to obtain the corresponding ciphertext character (Ci), as shown here:
Ci = (Pi + Ki) mod 26
At the receiver's end, the reverse process is followed to decrypt the ciphertext. That is, a ciphertext character (say, Ci) is added with the additive inverse of the respective subkey (denoted as, -Ki) and the result is mapped to Z26 using the modular arithmetic to obtain the corresponding plaintext character (Pi) as shown here:
Pi = (Ci - Ki) mod 26
An example given in Question 18 illustrates the encryption and decryption processes using the autokey cipher.
Playfair cipher
The Playfair cipher, also known as Playfair square, was used by the British army during World War I, and then by Australians during World War II. Despite its invention by Wheatstone in 1854, it is popularly known after the name of Lord Playfair, who heavily promoted its use. Here, the secret key is formed of 25 alphabets organized into a 5 × 5 matrix. (I and J are considered as same and inserted in the same cell in the matrix.) Different keys can be obtained from different possible arrangements of alphabets in the matrix.
The first step in the Playfair encryption technique is to create and populate the matrix. Initially, a keyword (or phrase) is chosen by the sender and receiver that may not necessarily contain all the 25 alphabets. To organize this keyword in the matrix, it is entered starting from the top left position to right (that is, row-wise), and from top to bottom. While entering, the duplicate letters in the keyword are dropped; that is, each letter of the keyword is entered only once. The remaining empty positions of the keyword matrix are filled with the alphabets (in order) that are not included in the keyword. Moreover, if either I or J appears in the keyword, both are ignored while filling the empty positions of the matrix. However, if neither I nor J appears in the keyword, both are placed at the same position in the matrix. This organization of 25 alphabets in the matrix becomes the secret key for encryption and decryption.
The next step is to encrypt the plaintext. However, before encryption, the plaintext message is broken into diagraphs (group of two characters). If both characters in a pair are the same, then we insert a bogus letter (say, X) between them to distinguish. In case the plaintext consists of an odd number of characters, then also a bogus character is inserted at the end of the plaintext to make the number of characters even. For example, if the plaintext is GREETING, then we have four groups of two letters each as GR, EE, TI, and NG. As the second pair of the message contains repeated letter E, the bogus letter X is inserted between two E's. Now, the pairs of the message become GR, EX, ET, IN and G. To make the number of characters even, the bogus character X is inserted at the end, making the last pair as GX.
At the sender's end, each pair of alphabets in the plaintext is encrypted using the following rules:
 If the two letters in a pair appear in the same row of the keyword matrix, they must be replaced with the letters at their immediate right positions. We must wrap around to the beginning of the row if the any of the letters appears at the end of the row.
If the two letters in a pair appear in the same row of the keyword matrix, they must be replaced with the letters at their immediate right positions. We must wrap around to the beginning of the row if the any of the letters appears at the end of the row.
 If the two letters in a pair appear in the same column of the keyword matrix, they must be replaced with the letters at their immediate below positions. We must wrap around to the beginning of the column if any of the letters is the last letter in the column.
If the two letters in a pair appear in the same column of the keyword matrix, they must be replaced with the letters at their immediate below positions. We must wrap around to the beginning of the column if any of the letters is the last letter in the column.
 If the two letters in a pair do not appear in the same row or column of the keyword matrix, each of them must be replaced with the letter placed at the intersecting position of its own row and the column of another.
If the two letters in a pair do not appear in the same row or column of the keyword matrix, each of them must be replaced with the letter placed at the intersecting position of its own row and the column of another.
At the receiver's end, the ciphertext is decrypted using the same rules as for encryption, with some differences. If the two letters of a pair in the ciphertext satisfy the condition of rule 1, they are replaced with the letters at their immediate left positions. If the two letters of a pair in the ciphertext satisfy the condition of rule 2, they are replaced with the letters at their immediate above positions. The rule 3 is same for decryption. During decryption, the bogus letters are also removed. An example given in Question 19 illustrates the encryption and decryption processes using the Playfair cipher.
Vigenere cipher
The Vigenere cipher has been named after its designer Blaise de Vigenere. In this cipher, the group of subkeys used depends on the position of the characters in the plaintext, rather than the character itself. Thus, the group of subkeys can be created independent of the plaintext. The initial secret key of length n (where 1 ≤ n ≤ 26) is chosen by the sender and receiver. Then, the chosen key is repeated till the end of the plaintext. That is, if the initial secret key chosen is(K1, K2,…, Km), then the set of keys used for encryption and decryption will be K=[(K1, K2,…, Km), (K1, K2,…, Km),…]. Thus, this cipher helps to encrypt plaintext of any size.
At the sender's end, each plaintext character (Pi) is added with the respective key character (Ki) and the result is mapped to Z26 using the modular arithmetic to obtain the corresponding ciphertext character (Ci) as shown here:
Ci = (Pi + Ki) mod 26
At the receiver's end, the reverse process is followed to decrypt the ciphertext. That is, a ciphertext character (say, Ci) is added with the additive inverse of the respective key character (denoted as, -Ki) and the result is mapped to Z26 using the modular arithmetic to obtain the corresponding plaintext character (Pi) as shown here:
Pi = (Ci - Ki) mod 26
An example given in Question 20 illustrates the encryption and decryption processes using the Vigenere cipher.
Hill cipher
The Hill cipher was invented in 1929 by Lester S. Hill, and it is named after him. In the Hill cipher, the plaintext is first divided into equal-size blocks. Then, the blocks are encrypted in such a way that each block element (character) participates in the encryption of other block elements in the block. The key (K) used in the Hill cipher is in the form of an n×n square matrix, where n is the block size (see Figure 3.5). Each element of the key matrix is represented as Kij, where 1 ≤ i, j ≤ n.
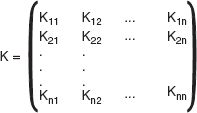
Figure 3.5 Key Matrix
Consider a plaintext block (P) that contains n characters is to be encrypted. Let P1, P2,…, Pn represent the plaintext characters in this block and their corresponding ciphertext characters are represented as C1, C2,…, Cn. Then, we get the ciphertext as shown here:
C1 = (P1K11 + P2K21 + … + PnKn) mod 26C2 = (P1K12 + P2K22 + … + PnKn2) mod 26...Cm = (P1K1n + P2K2n + … + PnKnn) mod 26
The preceding equations can be expressed as:

In general, the encryption in the Hill cipher can be expressed as shown here:
C = K P mod 26
To perform decryption at the receiver's end, the inverse of the key is first determined in Z26, and then the ciphertext is decrypted, as shown here:
P = K-1 C mod 26
An example given in Question 21 illustrates the encryption and decryption processes using the Hill cipher.
7. What are keyless and keyed transposition ciphers?
Ans.: Keyless and keyed ciphers are two categories of transposition ciphers that reorder (permute) the symbols of plaintext to form ciphertext. These are described as follows:
 Keyless transposition ciphers: These are the traditional ciphers, and are easy to use. They do not use any key to permute the characters in the plaintext and thus, are named as keyless ciphers. To permute the characters, the plaintext characters are written in a table either column-wise or row-wise. In the former case, ciphertext is formed by reading the characters from the table row-wise, while in the latter case, column-wise.
Keyless transposition ciphers: These are the traditional ciphers, and are easy to use. They do not use any key to permute the characters in the plaintext and thus, are named as keyless ciphers. To permute the characters, the plaintext characters are written in a table either column-wise or row-wise. In the former case, ciphertext is formed by reading the characters from the table row-wise, while in the latter case, column-wise.
 Keyed transposition ciphers: These ciphers make use of a key to permute the characters in the plaintext and, thus, are named as keyed ciphers. These ciphers first divide the plaintext into blocks of predefined size, and then a key is used to permute the characters within each block individually.
Keyed transposition ciphers: These ciphers make use of a key to permute the characters in the plaintext and, thus, are named as keyed ciphers. These ciphers first divide the plaintext into blocks of predefined size, and then a key is used to permute the characters within each block individually.
8. Write a short note on columnar transposition ciphers.
Ans.: A columnar transposition cipher is the combination of keyless and keyed transposition ciphers. It performs encryption and decryption in three steps; the first and third steps are keyless, while the second step is performed on the basis of a key. The plaintext characters are first arranged in the table row-wise. Secondly, these characters are permuted by reordering the columns based on a key. And, finally, the characters are read from the new table column-wise.
To understand, consider the plaintext ‘hellohowareyou', and the key ‘BACKIN’. Initially, the plaintext characters are arranged in the table row-wise, as shown in the following. The rows are padded with extra characters to fill the table, if required.
After arranging the plaintext, the letters of the key BACKIN are numbered according to the alphabetical order. For example, A is assigned the number 1, B is 2, C is 3, I is 4, K is 5 and N is 6. Now, the columns of the table are reordered according to numbers assigned to the key letters. For example, the column 1 is interchanged with column 2, column 4 with column 5, while columns 3 and 6 remain intact. After reordering the columns, the new table is as shown in the following:
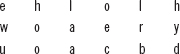
The characters are now read out column-wise from the new table to form the ciphertext. That is, the ciphertext is ‘ewuhoolaaoeclrbhyd’.
9. What is the difference between stream cipher and block cipher?
Ans.: Stream cipher and block cipher are two categories of symmetric ciphers.
 Stream cipher: This cipher operates on one symbol (character) of plaintext at a time and produces a corresponding symbol of ciphertext. As the name of the cipher implies, we have a plaintext stream
Stream cipher: This cipher operates on one symbol (character) of plaintext at a time and produces a corresponding symbol of ciphertext. As the name of the cipher implies, we have a plaintext stream P =(P1,P2,P3,…), a ciphertext stream C=(C1,C2,C3,…), and a key stream K=(K1, K2, K3,…). The plaintext characters are input into the encryption algorithm, one character at a time. The encryption algorithm uses the respective subkey to encrypt each plaintext character, which results in a corresponding ciphertext character. Each character is encrypted and decrypted using the same key, regardless of the fact that multiple keys are being used. For example, consider that the plaintext is ‘user’ and the key stream used is (K1, K2 and K3). Now, the plaintext is encrypted such that the characters ‘u’ and ‘r’ are encrypted using the key K1, the characters ‘s’ is encrypted using the key K2 and the character ‘e’ is encrypted using K3. During decryption also, the same set of keys (K1, K2 and K3) is used, such that the characters ‘u’ and ‘r’ are decrypted using the key K1, the character ‘s’ is decrypted using the key K2 and the character ‘e’ is decrypted using the key K3. The Additive cipher and Vigenere cipher can be categorized as stream ciphers.
 Block cipher: This cipher encrypts a group or block (with size > 1) of symbols in plaintext at one time, producing a block of ciphertext of the same size. Similarly, during decryption, a block of ciphertext symbols is converted back to a block of plaintext with one block at a time. A single key is used to encrypt or decrypt the entire block, even if the key contains multiple values. The Hill cipher and Playfair cipher can be categorized as block ciphers.
Block cipher: This cipher encrypts a group or block (with size > 1) of symbols in plaintext at one time, producing a block of ciphertext of the same size. Similarly, during decryption, a block of ciphertext symbols is converted back to a block of plaintext with one block at a time. A single key is used to encrypt or decrypt the entire block, even if the key contains multiple values. The Hill cipher and Playfair cipher can be categorized as block ciphers.
10. Explain the term one time pad.
Ans.: The one-time pad (also known as the Vernam cipher) was first implemented at AT&T using a device called the Vernam machine. It is actually a random set of non-repeating characters that is used as a key for generating the ciphertext message. As the name suggests, the set of characters can be used only once and, therefore, cannot be used for any other message. The algorithm used in generating a ciphertext message by the one-time pad scheme is as follows:
1. The alphabets in the plaintext are assigned numbers in an increasing order. For example, A = 0, B = 1,…, and Z = 25.
2. The one-time pad alphabets are randomly chosen, and numbers are assigned in the same manner as in the plaintext. For example, C = 2, D = 3 and so on.
3. The numbers that correspond to the plaintext and the one-time pad input are added.
4. Then the mod 26 operation is done with each generated character of the sum.
5. The numbers obtained from the sum are translated back to the corresponding alphabet, which gives the output ciphertext.
The security of the one-time pad method is very high because of its randomness and one-time use. Thus, it can only be used for small plaintext messages. The ciphertext message generated using the one-time pad method is also random; that is, the same ciphertext message is not generated for two same plaintexts, thus making it less vulnerable to attacks. In spite of these benefits, it faces some difficulties in practical implementation. One problem is that it is difficult to generate a large set of random numbers each time for the same nodes to communicate with each other. Another problem is that of key distribution and protection, as a key of equal length is needed by both the sender and the receiver in every message exchange. An example illustrating the use of one-time pad is shown in Question 22.
11. What do you understand by bit-oriented ciphers? Why do we need them?
Ans.: The ciphers that perform encryption or decryption at the bit level rather than at the character level are referred to as bit-oriented ciphers. Earlier, most of the information to be encrypted was in textual form; thus, the use of character-oriented ciphers was justified. However, these days, the information to be encrypted is not just text, but may comprise graphics, audio and video. Thus, bit-oriented ciphers are needed, because such types of data can be conveniently transformed into streams of bits, which can then be encrypted and sent to the intended receiver. Moreover, as the text is treated at the bit level, each character of plaintext can be replaced with 8 bits or 16 bits. This increases the number of symbols in the plaintext by 8 or 16 times, thereby also increasing the security.
12. What do you mean by modern block cipher? What are its components?
Ans.: The modern block cipher is a bit-oriented symmetric-key cipher that encrypts an m-bit block of plaintext at a time to produce an m-bit block of ciphertext. Similarly, during decryption, an m-bit block of ciphertext is converted back to an m-bit block of plaintext, one block at a time. Each block of bits is encrypted or decrypted using the k-bit key (see Figure 3.6). The decryption algorithm used is the inverse of the encryption algorithm, and the same secret key is used for both encryption and decryption. Thus, the same block of plaintext is always encrypted to same block of ciphertext.

Figure 3.6 Modern Block Cipher
If the plaintext contains less than m bits, extra bits (padding) are added to make it an m-bit block. On the other hand, if the plaintext contains more than m bits, the plaintext is divided into blocks of m bits each and extra bits are added to the last block to make it an m-bit block if it contains less than m bits.
The modern block cipher consists of various components, described as follows:
 S-box: This is a substitution box having the same characteristics as that of the substitution cipher, except that the substitution of several bits is performed in parallel. It takes
S-box: This is a substitution box having the same characteristics as that of the substitution cipher, except that the substitution of several bits is performed in parallel. It takes n bits of plaintext at a time as input and produces m bits of ciphertext as output, where the value of n and m may be the same or different. An S-box can be keyed or keyless. In a keyed S-box, the mapping of n inputs to m outputs is decided with the help of a key, whereas in a keyless S-box, the mapping from inputs to outputs is predetermined. Usually, keyless S-boxes are used in modern block ciphers.
 P-box: This is a permutation box having the same characteristics as that of the traditional transposition cipher, except that it performs transposition at the bit-level, and that transposition of several bits is performed at the same time. The input bits are permuted to produce the output bits. For example, the first input bit can be the second output bit, the second input bit can be the third output bit and so on. A P-box is sometimes also referred to as a D-box (diffusion box). It is normally a keyless cipher and can be classified into the following three types (see Figure 3.7), based on the length of input and output:
P-box: This is a permutation box having the same characteristics as that of the traditional transposition cipher, except that it performs transposition at the bit-level, and that transposition of several bits is performed at the same time. The input bits are permuted to produce the output bits. For example, the first input bit can be the second output bit, the second input bit can be the third output bit and so on. A P-box is sometimes also referred to as a D-box (diffusion box). It is normally a keyless cipher and can be classified into the following three types (see Figure 3.7), based on the length of input and output:
 Straight P-box: This P-box takes
Straight P-box: This P-box takes n bits as input, permutes them and produces n bits as output. As the number of inputs and outputs is the same, there are a total of n! ways to map n inputs to n outputs.
 Compression P-box: This P-box takes
Compression P-box: This P-box takes n bits as input and permutes them in such a way that an output of m bits is produced, where m < n. This implies that some of the inputs are blocked and do not reach the output. Compression P-boxes are used in those situations where we need to permute the bits and at the same time need lesser number of bits at each successive stage.
 Expansion P-box: This P-box takes
Expansion P-box: This P-box takes n bits as input and permutes them in such a way that an output of m bits is produced, where m > n. This implies that a single input is mapped to more than one output. The expansion P-boxes are used in those situations where we want a higher number of bits at each successive stage.
 Circular shift: Another important component involved in modern block cipher is the circular shift operation, which tends to conceal the bit patterns in a transmitted word. The bits can be shifted either in the left or the right direction. In a circular left shift operation [see Figure 3.8 (a)], every bit of an
Circular shift: Another important component involved in modern block cipher is the circular shift operation, which tends to conceal the bit patterns in a transmitted word. The bits can be shifted either in the left or the right direction. In a circular left shift operation [see Figure 3.8 (a)], every bit of an m-bit word is shifted by a specific number of positions (say, n) in the left direction. In other words, the n leftmost bits of the word are removed and placed at the rightmost positions. The reverse happens in a circular right-shift operation [see Figure 3.8 (b)], where each bit of an m-bit word is shifted by n positions in the right direction. That is, the n rightmost bits of the word are removed and placed at the leftmost position. The circular shift operation can be either keyed or keyless. In the former case, the key defines the number of positions by which the bits are to be shifted. On the other hand, in the latter case, the number of positions to be shifted is usually fixed and predetermined. It is important to note that if a circular left shift operation is used in encryption, then a circular right shift operation is used in decryption, and vice-versa. Thus, both these operations are inverses of each other.

Figure 3.7 Types of P-Boxes

Figure 3.8 Circular Shift Operati
13. Explain Shannon's theory of diffusion and confusion.
Ans.: The theory of diffusion and confusion was proposed by Claude Shannon in attempt to thwart cryptanalysis based on statistical analysis. Both diffusion and confusion are the essential properties of block ciphers. Diffusion is based on the idea of hiding the relationship between the ciphertext and plaintext. This will frustrate a cryptanalyst who examines the ciphertext statistics in order to determine the plaintext. To achieve diffusion, a ciphertext symbol must depend on some or all symbols in the plaintext. That is, a change in a single symbol in the plaintext causes change in several or all symbols in the ciphertext.
On the other hand, confusion is based on the idea of hiding the relationship between the ciphertext and the key. This will frustrate a cryptanalyst who attempts to determine the key using the ciphertext. To prevent intruders from discovering the key, confusion attempts to make the relationship between the value of encryption key and the statistics of ciphertext as complex as possible. This can be achieved by making sure that a ciphertext symbol depends on some or all symbols of the key used. That is, a change in a single bit of the key causes changes in several or all symbols in the ciphertext.
14. What is a product cipher?
Ans.: The concept of product cipher was proposed by Shannon. The basic idea of a product cipher is to build a complex cipher by combining two or more ciphers (transformations) in such a manner that the resulting cipher is more secure than the individual components. That is, various transformations, including substitutions, permutations, circular shifts and transposition, are combined within a single unit to make a complex cipher, known as product cipher. The complexity of a product cipher makes it more secure and resistant to various attacks, thereby making it more difficult for a cryptanalyst to thwart the security. All modern ciphers are product ciphers, and are classified into two categories on the basis of the type of components used in them, namely, Feistel and non-Feistel ciphers.
15. Explain Feistel cipher and its structure.
Ans.: The Feistel cipher, proposed by Horst Fiestel, belongs to a class of product ciphers that permits the use of invertible as well as noninvertible components. The Feistel cipher uses three types of components (units), namely, self-invertible, invertible and noninvertible components. This cipher works by combining all noninvertible units into a single unit and then using the same unit in encryption and decryption algorithms. Now, the problem is that since both encryption and decryption algorithms use noninvertible units, how can they be the inverses of each other? To resolve this problem, we use the XOR operation, so that the effects of a noninvertible component in encryption can be cancelled out during decryption.
Initially, a basic model of the Fiestel cipher was proposed, which had certain shortcomings. To overcome these shortcomings, the basic model was improved, resulting in the final design. Here, we will discuss both the designs.
Basic model
In this structure, the plaintext is divided into two equal-length blocks: left and right. During encryption, a noninvertible function (f), which accepts key (K) as an input, is applied to the right block of the plaintext (denoted as Rp), and the resultant output is XOR-ed with the left block (denoted as Lp). The output of the XOR operation becomes the left block of the ciphertext (denoted as Lc), while the right block of ciphertext (denoted as Rc) is same as the right block of plaintext. The function f and the XOR operation together are referred to as the mixer, which is self-invertible in nature. During decryption, the reverse process is followed. However, the input to the function f remains the same in both the encryption and decryption processes, as shown in Figure 3.9.

Figure 3.9 Basic Model of Fiestel Cipher
To verify the correctness of the design, we need to ensure that the encryption and decryption algorithms are inverses of each other. That is, it must be proved that Lp = Lp' and Rp = Rp'. To prove this, let us assume that there is no change in the ciphertext during transmission, which means Lc = Lc' and Rc=Rc'. As Rc = Rp and Rc' = Rp', we have Rp' = Rp.
Now, we can write that

As we know that Lc = Lp and  f(Rp,K)
f(Rp,K)Rc = Rp, the equation (1) can be written as:

Hence, the decryption algorithm produces the same plaintext as used by the encryption algorithm. In other words, the encryption and decryption algorithms are the inverses of each other.
Final design of the Feistel cipher
In the basic model of the Feistel cipher, the right block of the plaintext never changes and remains the same in the ciphertext also. Due to this, the generated ciphertext becomes vulnerable to attacks and is more prone to interception by a hacker. Thus, the design was improved by including the following enhancements:
 The number of rounds was increased in the final design.
The number of rounds was increased in the final design.
 A new element called swapper was added to each round. The role of the swapper is to swap the left and right blocks in each round. In addition, the effect of the swapper during encryption is cancelled out with the effect of the swapper during decryption.
A new element called swapper was added to each round. The role of the swapper is to swap the left and right blocks in each round. In addition, the effect of the swapper during encryption is cancelled out with the effect of the swapper during decryption.
 Two round keys (
Two round keys (K1 and K2) are used during encryption and decryption. The encryption and decryption algorithms use the keys in reverse order.
Figure 3.10 shows the final design of the Feistel cipher with two rounds.
The mixers and swappers used in encryption and decryption are inverses of each other, respectively. This implies that the encryption and the decryption algorithms are also inverses of each other. To prove this fact, we need to show that Lp = Lp' and Rp = Rp'. To prove this, let us assume that there is no change in the ciphertext during transmission, which means Lc = Lc' and Rc = Rc'. First, we will prove the equality between the middle texts (L and L', R and R'), and then between the final text. As R' = Lc', Lc' = Lc and Lc = R, we have R' = R.
We can write that:

As we know that Rc= and  f(R,K2)
f(R,K2)Lc=R, Equation (2) can be written as:
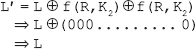
Now, we have Rp'=L', L'=L and L=Rp. Thus, it is proved that Rp' = Rp.

Figure 3.10 Final Design of Fiestel Cipher with two Rounds
We can also write that:

As R'=R and L'=L, Equation (3) can be written as:

As we know that L=Rp and R=Lp, Equation (4) can be written as: f(Rp,K1)
f(Rp,K1)
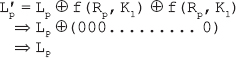
Hence, the decryption algorithm produces the same plaintext as used by the encryption algorithm. In other words, encryption and decryption algorithms are the inverses of each other.
16. What is a non-Feistel cipher?
Ans.: A non-Feistel cipher uses only invertible components. Each element in the plaintext has a respective element in the cipher. For example, if an S-box is used, then it must have the same number of inputs and outputs. In addition, only the straight P-boxes can be used, because the compression and expansion P-boxes are non-invertible in nature. Unlike the Fiestel cipher, it is not required to break the plaintext into two halves in a non-Fiestel cipher.
17. Encrypt the message ‘this is an exercise’ using the following ciphers. Ignore the spaces between the words while encrypting. Also, decrypt the message to get the original plaintext.
(a) Additive cipher with key = 20
(b) Multiplicative cipher with key = 15
(c) Affine cipher with key = (15, 20)
Ans.: (a) Additive cipher with key = 20
Plaintext (P) = ‘this is an exercise’
Key (K) = 20
 Encryption: In additive cipher, the ciphertext
Encryption: In additive cipher, the ciphertext (C) = (P + K) mod 26, which can be found as follows:

Hence, the corresponding ciphertext is ‘nbcmcmuhyrylwcmy’.
 Decryption: To decrypt the ciphertext (
Decryption: To decrypt the ciphertext (C), we first need to determine the additive inverse of 20 in Z26, which is equal to 6 (26–20). Now, the ciphertext (C) can be decrypted to obtain the plaintext (P) using the formula (C+6) mod 26, as shown here:

(b) Multiplicative cipher with key = 15
Plaintext (P) = ‘this is an exercise’
Key (K) = 15
 Encryption: In multiplicative cipher, the ciphertext
Encryption: In multiplicative cipher, the ciphertext (C) = (P * K) mod 26, which can be found as follows:

Hence, the corresponding ciphertext is ‘zbqkqkanihiveqki’.
 Decryption: To decrypt the ciphertext, first we need to determine the multiplicative inverse of 15 in
Decryption: To decrypt the ciphertext, first we need to determine the multiplicative inverse of 15 in Z26, which is equal to 7, as 15 * 7 ≡ 1 (mod 26). Now, the ciphertext (C) can be decrypted to obtain the plaintext (P) using the formula (C * 7) mod 26, as shown here:

(c) Affine cipher with key = (15, 20)
Plaintext (P) = ‘this is an exercise’
Key (K) = 15
 Encryption: In affine cipher, the plaintext (
Encryption: In affine cipher, the plaintext (P) is first encrypted using the multiplicative cipher and the first key (that is, 15) to produce the temporary ciphertext (C1). Then, C1 is again encrypted using the additive cipher and the second key (that is, 20) to produce the final ciphertext(C), as shown here:

Hence, the corresponding ciphertext is ‘tvkekeuhcbcpykec’.
 Decryption: First, the ciphertext (
Decryption: First, the ciphertext (C) is decrypted using the additive cipher and the additive inverse of key 20 to produce the temporary plaintext P1. Then, P1 is again decrypted using the multiplicative cipher and the multiplicative inverse of key 15. The additive inverse of key 20 in Z26 is 6, while the multiplicative inverse of key 15 in Z26 is 7. Now, the decryption is performed as shown here:

18. Encrypt the plaintext message ‘ATTACK SUCCESSFUL’ by using the initial key stream as 12 with the autokey cipher.
Ans.: The plaintext will be encrypted to form the ciphertext as shown here:

Hence, the corresponding ciphertext is ‘MTMTCMCMWEGWKXZF’.
19. Given the key ‘MONARCHY', apply the Playfair cipher to the plaintext ‘FACTIONALISM’. Decrypt the ciphertext also.
Ans.: The given keyword = ‘MONARCHY’
The corresponding keyword matrix is as follows:

Encryption
The given plaintext is ‘FACTIONALISM’. The different pairs of plaintext are FA, CT, IO, NA, LI and SM. These pairs are encrypted as follows:
 In the first pair, the letter F is at position (3, 2), and A is at position (1, 4) in the keyword matrix. That is, neither their rows nor their columns match. Thus, F is replaced with the letter at the intersecting position of the third row and fourth column, which is either I or J. Let us use I. Similarly, A is replaced with the letter at the intersecting position of the first row and second column, which is the letter O.
In the first pair, the letter F is at position (3, 2), and A is at position (1, 4) in the keyword matrix. That is, neither their rows nor their columns match. Thus, F is replaced with the letter at the intersecting position of the third row and fourth column, which is either I or J. Let us use I. Similarly, A is replaced with the letter at the intersecting position of the first row and second column, which is the letter O.
 For the next two pairs, CT and IO, neither the rows nor the columns match. Thus, using the same rule as earlier, they are replaced with DL and FA, respectively.
For the next two pairs, CT and IO, neither the rows nor the columns match. Thus, using the same rule as earlier, they are replaced with DL and FA, respectively.
 In the fourth pair, NA, both letters appear in the same row. Thus, they are replaced with the letters at their immediate right positions, which are A and R.
In the fourth pair, NA, both letters appear in the same row. Thus, they are replaced with the letters at their immediate right positions, which are A and R.
 In the last two pairs, LI and SM, neither the rows nor the columns match. Thus, they are replaced with SE and LA, respectively.
In the last two pairs, LI and SM, neither the rows nor the columns match. Thus, they are replaced with SE and LA, respectively.
Hence, the corresponding ciphertext is ‘IODLFAARSELA’.
Decryption
The different pairs of ciphertext are IO, DL, FA, AR, SE and LA. These pairs are decrypted as follows:
 In the first pair, the letter I is at position (3, 4) and O appears at position (1, 2) in the keyword matrix. That is, neither their rows nor their columns match. Thus, I is replaced with the letter at the intersecting position of third row and second column, which is F. Similarly, O is replaced with the letter at the intersecting position of first row and fourth column, which is the letter A.
In the first pair, the letter I is at position (3, 4) and O appears at position (1, 2) in the keyword matrix. That is, neither their rows nor their columns match. Thus, I is replaced with the letter at the intersecting position of third row and second column, which is F. Similarly, O is replaced with the letter at the intersecting position of first row and fourth column, which is the letter A.
 For the next two pairs, DL and FA, neither the rows nor the columns match. Thus, using the same rule as earlier, they are replaced with CT and IO, respectively.
For the next two pairs, DL and FA, neither the rows nor the columns match. Thus, using the same rule as earlier, they are replaced with CT and IO, respectively.
 In the fourth pair, AR, both letters appear in the same row. Thus, they are replaced with letters at their immediate left positions, which are N and A.
In the fourth pair, AR, both letters appear in the same row. Thus, they are replaced with letters at their immediate left positions, which are N and A.
 In the last two pairs, SE and LA, neither the rows nor the columns match. Thus, they are replaced with LI and SM, respectively.
In the last two pairs, SE and LA, neither the rows nor the columns match. Thus, they are replaced with LI and SM, respectively.
Hence, the corresponding plaintext is ‘FACTIONALISM’.
20. Encrypt the plaintext message ‘honesty is the best’ by using a 6-character key ‘CENTRE’ with the Vigenere cipher.
Ans.: The encryption process using the Vigenere cipher is shown here:

Hence, the corresponding ciphertext is ‘jsaxjxamfmyidifm’.
21. Given the key ‘GYBNQKURP', apply the Hill cipher to the plaintext ‘ACT’ to show how encryption and decryption are performed and prove authenticity.
Ans.: The given plaintext (P) = ‘ACT’
Key (K) = ‘GYBNQKURP’
The key used can be written as:

Encryption
The plaintext ACT can be written as:

Thus, the ciphertext (is) C given as PK mod 26 as shown here.

Hence, the corresponding ciphertext is ‘POH’.
Decryption
In order to decrypt the ciphertext, we first need to calculate the inverse of the key matrix and then multiply it with the ciphertext, that is, P = K-1C mod 26. Now, the inverse of the key matrix is:
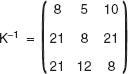
Thus, the plaintext can be obtained as shown here:
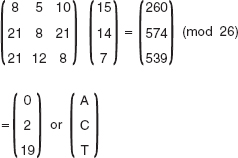
Since the receiver receives the same message as sent by the sender, the authenticity of the message is proved.
22. Generate the ciphertext message using the one-time pad algorithm for the plaintext message ‘higautam’.
Ans.:

Hence, the corresponding ciphertext is ‘ikfsptxf’.
Multiple-choice Questions
1. Which of the following is a monoalphabetic cipher?
(a) Caesar cipher
(b) Autokey cipher
(c) Vigenere cipher
(d) All of these
2. The __________ cipher is a combination of additive and multiplicative ciphers with a pair of keys.
(a) Affine
(b) Caesar
(c) Autokey
(d) Shift
3. In the polyalphabetic cipher, the characters in plaintext have a __________ relationship with the characters in ciphertext.
(a) One-to-one
(b) One-to-many
(c) Many-to-one
(d) Many-to-many
4. The Hill cipher belongs to the category of ciphers, named __________.
(a) Stream cipher
(b) Block cipher
(c) Both (a) and (b)
(d) None of these
5. The __________ cipher can be categorized as a stream cipher.
(a) Additive
(b) Hill
(c) Playfair
(d) None of these
6. Which of the following is/are components of a modern block cipher?
(a) Circular shift
(b) S-box
(c) P-box
(d) All of these
7. __________ is based on the idea of hiding the relationship between the ciphertext and the key.
(a) Diffusion
(b) Confusion
(c) Both (a) and (b)
(d) None of these
8. The concept of product cipher was proposed by __________.
(a) Verman
(b) Fiestel
(c) Lester S. Hill
(d) Shannon
9. The Feistel cipher uses the __________ operation.
(a) AND
(b) NOR
(c) XOR
(d) OR
10. A non-Feistel cipher uses only the __________ P-box.
(a) Compression
(b) Expansion
(c) Straight
(d) None of these
Answers
1. (a)
2. (a)
3. (b)
4. (b)
5. (a)
6. (d)
7. (b)
8. (d)
9. (c)
10. (c)
1. Explain DES with its structure. Also explain its function.
Ans.: Data Encryption Standard (DES) is a symmetric-key block cipher that was first published in 1977 by National Institute of Standards and Technology (NIST). It was originally proposed by IBM in 1973 in response to the request for proposals for a national symmetric-key cryptosystem. This encryption standard was adopted by the US government for non-classified information and by various industries for use in security products. DES is also known as the Data Encryption Algorithm (DEA) by ANSI and DEA-1 by ISO.
At the sender's end, DES divides the plaintext into 64-bit blocks and encrypts each block using a 56-bit cipher key to produce a 64-bit ciphertext block. At the receiver's end, the reverse process is followed; that is, DES decrypts the 64-bit ciphertext to obtain 64-bit plaintext. Being a symmetric-key cipher, DES uses the same 56-bit cipher key for both encryption and decryption. Originally, the cipher key is of 64 bits including 8 parity bits; however, the usable bits in key are only 56.
DES involves multiple rounds to produce ciphertext, and the key used in each round (called the round key) is the subset of the general key, called the cipher key; the round keys are generated by the round key generator. Thus, if there are P rounds in the cipher, then the round key generator produces total P round keys (K1, K2,…, KP) where K1 is used in first round, K2 in second round and so on.
DES Structure
Figure 4.1 shows the general structure of the DES encryption algorithm (referred to as the DES cipher); the design of the DES decryption algorithm (referred to as the DES reverse cipher) is also similar, except that the round keys are used in the reverse order from that of encryption. The whole process of producing ciphertext from plaintext comprises 19 stages. The first stage is the initial transposition, which performs keyless straight permutations that are the inverse of each other on the 64-bit plaintext block, according to a predetermined rule. The next 16 stages are the rounds that are functionally similar and, in each round, a different round key Ki of 48 bits derived from the cipher key of 56 bits is used. The second-last stage performs a swap function in which the leftmost 32 bits are exchanged with the rightmost 32 bits. The last stage, final transposition, is simply the opposite of the first stage; that is, it performs inverse transposition on the 64 bits received from the 32-bit swapper to generate
a 64-bit ciphertext block. For example, if in the initial transposition stage, the input bit 2 becomes the output bit 50, then in the final transposition stage, the input bit 50 becomes the output bit 2. At the receiver's end, the decryption is performed using the same key as in encryption; however, the steps are performed in the reverse order.
The structure of one of the 16 rounds (say, i-th round) during encryption in DES is shown in Figure 4.2. It takes two inputs: the leftmost 32 bits as left input (Li) and the rightmost 32 bits as right input (Ri), and produces two outputs, left output (Li+1) and right output (Ri+1), each of 32 bits. The left output (Li+1) is just the right input (Ri). The right output (Ri+1) is obtained by first applying the DES function (f) on the right input (Ri) and the 48-bit key (Ki) being used in the i-th round, denoted as f(Ri, Ki), and then performing the bitwise XOR of the result of DES function and the left input (Li). The structure of decryption round in DES is simply the opposite of the encryption round.

Figure 4.1 General Structure of DES Encryption

Figure 4.2 Structure of Encryption Round
DES Function
The essence of DES is the DES function, f(Ri, Ki). During each round, this function takes the -rightmost 32 bits and applies the 48-bit round key generated for that round on it to produce the 32-bit output. The function comprises four steps (see Figure 4.3), which are described as follows:
1. Expansion P-box: The right output (Ri) of 32 bits is initially fed into the expansion P-box, which expands it to 48 bits, because the key (Ki) used is of 48 bits. For this, the 32 bits of Ri are divided into eight blocks of 4 bits each. Each 4-bit block is then expanded to 6 bits using a predetermined rule, as explained in the following text.
a. Copy the input bits 1, 2, 3 and 4 to output bits 2, 3, 4 and 5, respectively.
b. Copy the input bit 4 of the previous block to output bit 1 of the block under consideration. This step is an exception to the first block.
c. Copy the input bit 1 of the next block to output bit 6 of the block under consideration. This step is an exception to the last (eighth) block.
Notice that in case of first block, the input bit 4 of the last block becomes the output bit 1, while in case of last block, the input bit 1 of the first block becomes the output bit 6. The resulting 48 bits are forwarded to the next step.
2. XOR operation: A bitwise XOR operation is performed on the 48-bit output obtained from the previous step and 48-bit round key Ki, resulting in 48 bits. These 48 bits are forwarded to the next step.
3. S-boxes: The 48-bit output obtained after the XOR operation is broken down into eight groups, with each group consisting of 6 bits. Each group of 6 bits is then fed to one of eight S-boxes. Each S-box follows a predetermined rule to map six inputs to four outputs and, thus, total 32 bits are obtained from eight S-boxes. The rule for substitution in each S-box is based on a table consisting of four rows and 16 columns. To perform the substitution in an S-box, the input bits 1 and 6 (2 bits) together define the row number, and the input bits 2, 3, 4 and 5 (4 bits) together define the column number. Now, the value at the intersection of the computed row and column number defines the 4 output bits. For example, if the input to an S-box is 101011, then the row number is 11 (equivalent to decimal number 3), and the column number is 0101 (equivalent to decimal number 5). Now, if the value at the intersection of third row and fifth column is 6, then the resulting output bits will be 0110.
4. Straight P-box: The 32 bits obtained from S-boxes are input to a straight P-box, which permutes them and produces 32 bits as output. As with the previous operations, the input bits are permuted based on the predetermined rule. For example, the input bit 7 becomes the output bit 2.

Figure 4.3 DES Function
2. Explain key generation of DES with the help of a block diagram.
Ans.: The generation of keys in DES for each round is done by round-key generator. The round-key generator produces sixteen 48-bit keys out of a 56-bit cipher key, one for each round. As in DES, the original key size is 64 bits, including the parity bits; therefore, the parity bits are initially dropped using the parity bit drop process before the actual key generation process starts. The parity bit drop process is actually a compression transposition step that drops the parity bits present at every eighth position (8, 16, 24, 32, 40, 48, 56 and 64) in the 64-bit key, generating a 56-bit key. Then the 56 bits of the key are permuted according to a predetermined rule, as shown in Table 4.1. For example, the bit 1 of the original 56-bit key becomes the eighth bit of the new 56-bit key. This 56-bit key is the actual cipher key used for key generation.
Table 4.1 Parity Drop Box Table

During each round, the round key generator uses the 56-bit cipher key and performs the following steps to generate the key for that round (see Figure 4.4).
1. Divide the plaintext into two halves of 28 bits each.
2. Perform circular left shift operation on each 28-bit half. Shifting is done either by 1 or 2 bits, depending on the round number. In case of rounds 1, 2, 9 and 16, shifting is done by 1 bit, while in the case of the other rounds, shifting is done by 2 bits.
3. After shifting has been performed, both halves are combined again to form a 56-bit part. These 56 bits are then given as input to the compression P-box.
4. The compression P-box, as its name suggests, compresses the 56-bit input to produce 48-bit output. This 48-bit output generated from the P-box is then used as a key for the round.

Figure 4.4 Key Generation in DES
3. Discuss the strength of DES.
Ans.: The strength of any cryptographic system is measured by the fact that how resistive it is to an attack. In case of DES, the strength of the system lies in two important aspects: key size and the use of S-boxes.
 Key size: DES uses 56-bit keys in each round, which means 256 (approximately 7.2 * 1016) number of keys. Therefore, a brute-force attack on DES seems practically impossible. However, if we assume that, to get the correct key, only half of the total keys are needed to be examined, a single computer performing one DES encryption per microsecond would still take more than 1000 years to break the DES.
Key size: DES uses 56-bit keys in each round, which means 256 (approximately 7.2 * 1016) number of keys. Therefore, a brute-force attack on DES seems practically impossible. However, if we assume that, to get the correct key, only half of the total keys are needed to be examined, a single computer performing one DES encryption per microsecond would still take more than 1000 years to break the DES.
 Use of S-boxes: DES uses eight S-boxes (substitution tables) in each round. The internal design of these substitution tables has been kept secret by IBM. Therefore, a suspicion has grown that there may be some weaknesses in the internal design of S-boxes that can be exploited by cryptanalysts to break the DES security. Over the years, a number of studies have appeared which suggest that there is a scope of attacking DES through S-boxes; however, no one has succeeded till date.
Use of S-boxes: DES uses eight S-boxes (substitution tables) in each round. The internal design of these substitution tables has been kept secret by IBM. Therefore, a suspicion has grown that there may be some weaknesses in the internal design of S-boxes that can be exploited by cryptanalysts to break the DES security. Over the years, a number of studies have appeared which suggest that there is a scope of attacking DES through S-boxes; however, no one has succeeded till date.
4. Comment on the weaknesses of DES.
Ans.: Although the DES cipher is widely used and is resistant to various attacks, some weaknesses are still found in it. The weaknesses have been found in two aspects of DES, in the cipher design and in the cipher key.
Weakness in the Cipher Design
The DES cipher involves a number of S-boxes and P-boxes, which suffer from certain problems. Some weaknesses found in S-boxes are as follows:
 In fourth S-box, the last 3 bits in the output can be obtained in the same way as the first bit in the output by performing complement operation on some of the bits in input.
In fourth S-box, the last 3 bits in the output can be obtained in the same way as the first bit in the output by performing complement operation on some of the bits in input.
 In a single round, the same output can be obtained if the bits in only three neighbouring S-boxes are changed.
In a single round, the same output can be obtained if the bits in only three neighbouring S-boxes are changed.
 Two specific chosen inputs when given to the array of eight S-boxes can result in the same output.
Two specific chosen inputs when given to the array of eight S-boxes can result in the same output.
Some weaknesses found in P-boxes are as follows:
 The initial and final permutation stages used in DES do not provide any security benefits.
The initial and final permutation stages used in DES do not provide any security benefits.
 In the expansion permutation used within the DES function, the input bits 1 and 4 of each 4-bit series are repeated in the output.
In the expansion permutation used within the DES function, the input bits 1 and 4 of each 4-bit series are repeated in the output.
Weakness in the Cipher Key
The cipher key used in DES has got certain shortcomings, which are described as follows:
 Size of cipher key: As the cipher key used in DES is of 56 bits, an intruder needs to examine 256 possible keys in order to attempt a brute-force attack. If a computer with a single processor that can process about one million keys per second is used for examining the whole key domain, it will take more than 2000 years to attempt brute-force attack on DES. In 1977, this period of 2000 years reduced to 120 days when 3500 networked computers and the concept of parallel processing were used. The entire key domain was divided into several parts, and each computer had to examine only some parts. Furthermore, a secret society having 42000 members can break the
cipher and thus, determine the key in 10 days only. Thus, it can be concluded that the DES with a cipher key of 56 bits is not safe enough for use.
Size of cipher key: As the cipher key used in DES is of 56 bits, an intruder needs to examine 256 possible keys in order to attempt a brute-force attack. If a computer with a single processor that can process about one million keys per second is used for examining the whole key domain, it will take more than 2000 years to attempt brute-force attack on DES. In 1977, this period of 2000 years reduced to 120 days when 3500 networked computers and the concept of parallel processing were used. The entire key domain was divided into several parts, and each computer had to examine only some parts. Furthermore, a secret society having 42000 members can break the
cipher and thus, determine the key in 10 days only. Thus, it can be concluded that the DES with a cipher key of 56 bits is not safe enough for use.
 Weak keys: Out of 256 keys, there are four keys that comprise either all 0s, all 1s or half 0s and half 1s. These four keys are referred to as the weak keys. When the round keys are created from any of the weak keys, they follow the same pattern as that of the cipher key. For example, a round key created from the weak key containing all 0s or all 1s will also comprise all 0s or 1s, respectively. This is because the cipher key is divided into two equal parts during key generation in DES. Thus, neither substitution nor permutation affects the block containing all 1s or all 0s. The disadvantage of using a weak key lies in the fact that it is the inverse of itself. That is, when a plaintext block is encrypted with a weak key and then the result is further encrypted with the same weak key, we get back the original plaintext block. Exploiting this fact, the intruder can easily attempt to decrypt the intercepted ciphertext using the weak keys. In case the result is the same after two decryptions, it means the intruder has got the key. Therefore, it is recommended that the use of weak keys be avoided.
Weak keys: Out of 256 keys, there are four keys that comprise either all 0s, all 1s or half 0s and half 1s. These four keys are referred to as the weak keys. When the round keys are created from any of the weak keys, they follow the same pattern as that of the cipher key. For example, a round key created from the weak key containing all 0s or all 1s will also comprise all 0s or 1s, respectively. This is because the cipher key is divided into two equal parts during key generation in DES. Thus, neither substitution nor permutation affects the block containing all 1s or all 0s. The disadvantage of using a weak key lies in the fact that it is the inverse of itself. That is, when a plaintext block is encrypted with a weak key and then the result is further encrypted with the same weak key, we get back the original plaintext block. Exploiting this fact, the intruder can easily attempt to decrypt the intercepted ciphertext using the weak keys. In case the result is the same after two decryptions, it means the intruder has got the key. Therefore, it is recommended that the use of weak keys be avoided.
 Semi-weak keys: In 256 keys, there are six pairs of keys that create only two distinct round keys for total 16 rounds, and each key is used in eight rounds. These six key pairs are referred to as semi-weak keys. Each pair of semi-weak keys creates the same two round keys; however, they are used in 16 rounds in different order.
Semi-weak keys: In 256 keys, there are six pairs of keys that create only two distinct round keys for total 16 rounds, and each key is used in eight rounds. These six key pairs are referred to as semi-weak keys. Each pair of semi-weak keys creates the same two round keys; however, they are used in 16 rounds in different order.
 Possible weak keys: There are 48 such keys that create only four different round keys, and each of them is repeated four times. These 48 keys are referred to as possible weak keys.
Possible weak keys: There are 48 such keys that create only four different round keys, and each of them is repeated four times. These 48 keys are referred to as possible weak keys.
 Key complement: In 256 keys, half of the keys (that is, 255) are the complement of the other half keys. That is, if half of the total keys are known, the remaining half can be obtained by simply inverting the bits (1 to 0 or 0 to 1) of the known keys. This proves to be beneficial to the intruder as now he or she has to examine only half of the key domain to attempt a brute-force attack. This is because of the fact that if the complement of plaintext is encrypted using the complement of a key, then a complement of the ciphertext is obtained.
Key complement: In 256 keys, half of the keys (that is, 255) are the complement of the other half keys. That is, if half of the total keys are known, the remaining half can be obtained by simply inverting the bits (1 to 0 or 0 to 1) of the known keys. This proves to be beneficial to the intruder as now he or she has to examine only half of the key domain to attempt a brute-force attack. This is because of the fact that if the complement of plaintext is encrypted using the complement of a key, then a complement of the ciphertext is obtained.
 Key clustering: The situation where two or more different keys result in the same ciphertext from the same plaintext is referred to as key clustering. In DES, each pair of semi-weak keys is a key cluster.
Key clustering: The situation where two or more different keys result in the same ciphertext from the same plaintext is referred to as key clustering. In DES, each pair of semi-weak keys is a key cluster.
5. What do you understand by differential and linear cryptanalysis of DES?
Ans.: Differential cryptanalysis is a chosen-plaintext attack that was introduced by Eli Biham and Adi Shamir in 1990. The basic idea of this attack is to choose a pair of plaintexts having specific differences and then analysing the corresponding ciphertext pair. The attacker examines how these differences propagate in the ciphertexts as the plaintexts pass through the rounds of DES. Using the differences in the ciphertexts, the attacker determines the probability of different possible keys and, eventually, as ciphertexts are analysed progressively, the actual cipher key emerges. The designers of DES were aware of chosen-plaintext attacks; therefore, they used S-boxes and 16 rounds to encrypt the plaintext in DES. Doing so makes DES invulnerable to differential cryptanalysis as breaking a DES message by differential analysis will need either 247 chosen plaintexts or 255 known plaintexts. Although differential cryptanalysis attacks are much powerful than brute-force attacks, finding 247 chosen plaintexts or 255 known plaintexts is not practically possible. Moreover, if we increase the number of rounds in DES to 20, then a differential cryptanalysis attack needs 264 chosen plaintexts, which is practically impossible, because DES can only have 264 possible plaintexts.
Linear cryptanalysis is a cryptanalysis technique that was introduced by Mitsuru Matsui in 1993. It is a known-plaintext attack that is based on linear approximations. The idea is to perform the XOR operation on some bits in the plaintext and ciphertext together, and then take the XOR of the result; the final result is a single bit that will be the XOR of some bits in the key. The linear cryptanalysis attacks on DES are more vulnerable than differential cryptanalysis attacks, because the designers of DES had no idea about linear cryptanalysis attacks at the time of designing. Also, S-boxes are not very resistant to linear cryptanalysis. A linear cryptanalysis attack can break DES in 243 pairs of known plaintexts. However, it is not practically feasible to find so many pairs.
6. Define Avalanche effect and completeness effect. Also, discuss the strength of DES with regard to these.
Ans.: Both Avalanche effect and completeness are the desirable properties of a block cipher. These properties are described as follows:
 Avalanche effect: This property states that any small change made to the plaintext or the key should cause a significant change in the ciphertext. That is, change in a single bit in the plaintext should result in changes in multiple bits in the ciphertext. This property is desired because the lack of it would considerably reduce the key domain to be searched, thus making it easier for a cryptanalyst to attempt a brute-force attack. In general, an encryption method is considered to have a good avalanche effect if change in a single bit of plaintext results in a random change in approximately half of the bits in the ciphertext.
Avalanche effect: This property states that any small change made to the plaintext or the key should cause a significant change in the ciphertext. That is, change in a single bit in the plaintext should result in changes in multiple bits in the ciphertext. This property is desired because the lack of it would considerably reduce the key domain to be searched, thus making it easier for a cryptanalyst to attempt a brute-force attack. In general, an encryption method is considered to have a good avalanche effect if change in a single bit of plaintext results in a random change in approximately half of the bits in the ciphertext.
DES has been proved to be very strong with regard to the Avalanche effect. In DES, when two plaintext blocks having only a single bit difference are encrypted using the same key, the ciphertexts obtained do not have much resemblance. Similarly, when the same plaintext is encrypted using two neighbouring keys (keys with only a small difference), we obtain two significantly different ciphertexts.
 Completeness effect: This property states that each bit of the ciphertext should depend on -multiple bits of the plaintext or the key. It tightens the concept of avalanche effect even more by requiring that, for each modified bit in the plaintext or the key, the change in ciphertext must be distributed uniformly. In other words, completeness means that the avalanche effect spans across all pairs of bits in the plaintext and ciphertext, almost uniformly. DES represents a strong completeness effect because of the diffusion and confusion produced by the P-boxes and S-boxes used in the DES cipher.
Completeness effect: This property states that each bit of the ciphertext should depend on -multiple bits of the plaintext or the key. It tightens the concept of avalanche effect even more by requiring that, for each modified bit in the plaintext or the key, the change in ciphertext must be distributed uniformly. In other words, completeness means that the avalanche effect spans across all pairs of bits in the plaintext and ciphertext, almost uniformly. DES represents a strong completeness effect because of the diffusion and confusion produced by the P-boxes and S-boxes used in the DES cipher.
7. What is double DES? Explain the meet-in-the-middle attack.
Ans.: Double DES (2-DES) is the simplest version of multiple-DES. As the name implies, double DES performs DES encryption/decryption twice using two different keys (K1 and K2) of 56 bits each. This increases the key size to 112 bits, thus, increasing the cryptographic strength to double that of normal DES.
At the sender's end, the plaintext P is initially encrypted using DES with key K1 to obtain the temporary ciphertext T = EK1(P). Then, the temporary ciphertext T is again encrypted using DES with key K2 to obtain the final ciphertext C = EK2(T), that is, C = EK2(EK1(P)). At the receiver's end, the reverse process is followed to decrypt the ciphertext, and the keys are used in the reverse order of that of encryption. That is, first the ciphertext C is decrypted using DES with key K2 to obtain the temporary plaintext T′ = DK2(C), and then the temporary plaintext T′ is again decrypted using DES with key K1 to get back the original plaintext P = DK1(T′), that is, P = DK1(DK2(C)). Figure 4.5 shows the encryption and decryption processes in double DES.

Figure 4.5 Encryption and Decryption in Double DES
Meet-in-the-middle Attack
The use of key size of 112 bits implies that an attacker would need 2112 attempts, which is twice that of normal DES, to break the cipher key. However, this is not true because of the meet-in-the-middle attack that was introduced by Merkle and Hellman. In this attack, encryption is performed from one end, decryption is performed from the other and matching the result in the middle, and it is hence that the attack is named so.
The meet-in-the-middle attack is based on the observation that if we have C = EK2(EK1(P)), then we can have EK1(P)= DK2(C), that is, T = T′. To understand how this attack happens, let us consider that the attacker knows a plaintext block P and a ciphertext block C of some message. Now, to determine K1 and K2, the attacker may perform the following steps:
1. For each of the 256 possible values of K1, allocate a large table in the memory and perform the following:
a. Compute the temporary ciphertext T = EK1(P).
b. Store the value of T in the next available row of the table in memory.
After performing the preceding two steps, we get a table containing the values of the temporary ciphertext T.
2. For each of the 256 possible values of K2, perform the following:
a. Compute the temporary plaintext T′ = DK2(C).
b. Compare the value of T′ with all the values in the table of temporary ciphertext T.
c. If T′ matches with any value of T in the table, use the corresponding pair of K1 and K2 to encrypt and decrypt another known pair of plaintext (say, P′) and ciphertext (say, C′) blocks, respectively.
d. If EK1(P′)= DK2(C′), then K1 and K2 are the correct keys and can be used for remaining blocks of the message.
Though the meet-in-the-middle attack is possible on double-DES, it needs a lot of memory space to store the values of T. For example, if a 64-bit plaintext block and a 56-bit key are used, then 256 64-bit blocks (equivalent to 217 bytes) of memory would be needed, which is too high. This makes the meet-in-the-middle attack practically infeasible.
8. Write a short note on triple DES.
Ans.: To overcome the problem of meet-in-the-middle attack in double DES, triple DES (3-DES) was developed. As the name implies, it performs the DES encryption process thrice. There are two implementations of 3-DES: one with two keys, and another with three keys.
3-DES with Two Keys
This version uses two keys, say K1 and K2 of 56 bits each to perform encryption and decryption. At the sender's end, the following three steps are performed to produce ciphertext C from the plaintext P.
1. Encrypt the plaintext P using DES with key K1 to produce T = EK1(P).
2. Decrypt T using DES with key K2 to produce S = DK2(EK1(P)).
3. Encrypt S using DES with key K1 to produce ciphertext C = EK1(DK2(EK1(P))).
Similarly, during decryption, the following three steps are used to obtain plaintext P from ciphertext C.
1. Decrypt the ciphertext C using DES with key K1 to produce T′ = DK1(C).
2. Encrypt T′ using DES with key K2 to produce S′ = EK2(DK1(C)).
3. Decrypt S′ using DES with key K1 to get back the original plaintext P = DK1(EK2(DK1(C))).
The use of two keys in 3-DES increases the key size to 112 bits and provides more secure communication. In addition, there is no special significance of using decryption in the second step. It is simply used to provide backward compatibility with the original DES by putting K1 = K2. In case of K1 = K2, 3-DES becomes equivalent to single DES and, thus, enables the users of 3-DES to decrypt the data encrypted by the users of single DES.
3-DES with Three Keys
This version uses three keys of 56 bits each, and a different key is used for performing encryption/decryption in each step. At the sender's end, the plaintext P is encrypted to form ciphertext C, as shown here:
c = EK3(DK2(EK1(P)))
At the receiver's end, the keys are used in the reverse order from that of encryption to obtain the original plaintext P from the ciphertext C, as shown here:
P = DK1(EK2(DK3(C)))
The use of three different keys increases the key length to 168 bits, making 3-DES three-key version more secure; however, it results in an increased overhead due to managing and transporting one more key. Here, the backward compatibility with DES is provided by having either K1 = K2 or K2 = K3.
9. Explain IDEA encryption and decryption in brief.
Ans.: The International Data Encryption Algorithm (IDEA) is a patented and universally applicable block cryptographic algorithm. It was proposed and launched in 1990 by Xuejia and James, and was initially named as Proposed Encryption Standard (PES). In 1991, some improvements were made in PES, and the new improved version was given the name Improved PES (IPES). Then, it was renamed to IDEA in 1992.
IDEA is a block cipher and is considered one of the strongest cryptographic algorithms. It offers effective protection of stored and transmitted data against unauthorized access by third parties. It uses a 128-bit-long key and both diffusion and confusion for encryption. This makes it more secure than the widely known DES, which is based on the use of a 56-bit key. However, as with DES, IDEA also operates on 64-bit plaintext blocks, and uses the same algorithm for encryption and decryption.
Though IDEA is powerful and strong, it is not as popular as DES because of two reasons. Firstly, it is not free and must be licensed before being used for commercial purposes. Secondly, IDEA keeps only a few history and track records as compared to DES. However, one popular e-mail privacy technique called Pretty Good Privacy (PGP) is based on IDEA.
Working of IDEA
Figure 4.6 shows the broad-level steps involved in the IDEA encryption process. The IDEA algorithm breaks down the 64-bit input data block into four 16-bits data blocks: P1, P2, P3 and P4. These four data blocks are then processed through eight rounds, and each round uses six 16-bit sub-keys generated from the original key. During each round, these data blocks are transformed by applying various arithmetic operations among each other and with the sub-keys. The whole encryption process uses a total of 52 sub-keys (K1 to K52), out of which six sub-keys, K1 to K6, are used in the first round. In the second round, the next six sub-keys, K7 to K12, are used and so on. Finally, the sub-keys K43 to K48 are used in the eighth round. The final step of the encryption process is output transformation, which uses four sub-keys, K49 to K52. The output produced from this step is four blocks of ciphertext: C1, C2, C3 and C4, each of 16 bits, which are then concatenated to form the final 64-bit ciphertext block.

Figure 4.6 IDEA Encryption Process
Encryption Round
Each round of the IDEA encryption process performs a sequence of operations on four plaintext blocks using the corresponding six sub-keys. These operations include XOR, addition and multiplication. It may be noted that addition and multiplication operations here do not imply the ordinary addition and multiplication; rather, they are addition modulo 216 and multiplication modulo (216+1), respectively. The steps involved in an encryption round are as follows:
1. Multiply P1 and K1.
2. Add P2 and K2.
3. Add P3 and K3.
4. Multiply P4 and K4.
5. XOR the results of step 1 and step 3.
6. XOR the results of step 2 and step 4.
7. Multiply the results of step 5 with K5.
8. Add the results of steps 6 and 7.
9. Multiply the results of step 8 with the K6.
10. Add the results of step 7 and step 9.
11. XOR the results of step 1 and step 9 and store the result in R1.
12. XOR the results of step 3 and step 9 and store the result in R2.
13. XOR the results of step 2 and step 10 and store the result in R3.
14. XOR the results of step 4 and step 10 and store the result in R4.
15. Swap the blocks R2 and R3.
The resultant data blocks R1, R2, R3 and R4 in each round are passed to the next round. Note that the eighth round does not involve the last step (step 15); that is, it does not perform the swapping of blocks R2 and R3. After performing all the eight rounds, the final data blocks, R1, R2, R3 and R4, of 16 bits each are passed to the next stage – that is, output transformation.
Output Transformation
This stage applies four keys, K49 to K52, on the input data blocks, R1, R2, R3 and R4, and produces the four ciphertext blocks, C1, C2, C3 and C4, by performing the following steps:
1. Multiply R1 and K49 to obtain C1.
2. Multiply R2 and K50 to obtain C2.
3. Multiply R3 and K51 to obtain C3.
4. Multiply R4 and K52 to obtain C4.
Finally, the four ciphertext blocks (C1, C2, C3 and C4) are combined to form a 64-bit ciphertext block.
Decryption
The decryption process of IDEA is the same as that of the encryption process; however, the sub-keys are used in the reverse order from that of encryption. The sub-keys used for decryption are the inverse of the sub-keys used for encryption.
Strength of IDEA
The IDEA algorithm is resistant to all known cryptanalysis attacks. It uses a 128-bit-long key. Therefore, to attempt a cryptanalysis attack on IDEA, the attacker needs to perform 2128 encryption operations, which is practically infeasible.
10. Explain the sub-key generation in the IDEA algorithm.
Ans.: As each round in the IDEA algorithm uses six sub-keys of 16-bit each and the output transformation step also needs four sub-keys, thus, a total of 52 16-bit sub-keys are required from the key length of 128 bits. For this, a sub-key generation process is used, which generates the sub-keys as follows:
 In the first round, six sub-keys of 16 bits each, that is, 96 bits, are required. Therefore, the first 96 bits of 128-bit key (say,
In the first round, six sub-keys of 16 bits each, that is, 96 bits, are required. Therefore, the first 96 bits of 128-bit key (say, K) are used for the first round. The rest of the key bits (97–128) remain unused and, thus, are kept for the second round.
 The second round also requires six sub-keys of 16 bits each; that is, a total of 96 bits. However, we have only 32 unused bits of the key
The second round also requires six sub-keys of 16 bits each; that is, a total of 96 bits. However, we have only 32 unused bits of the key K and, therefore, we need 64 bits more. To generate the rest of the bits, the IDEA algorithm uses the key shifting technique. In this technique, the original 128-bit key K is shifted left circularly by 25 bits. After shifting, the 26-th bit of the original key K becomes the first bit of the new key (say, K′), and the 25-th bit of key K becomes the 128-th bit of key K′. Now, the bits 1 to 64 of key K′ and the unused 32 bits (97–128) of key K are used to form six 16-bit sub-keys for the second round.
 In the third round, we have 64 unused bits of key
In the third round, we have 64 unused bits of key K′ generated in the second round, and 32 bits are still required. Thus, the key shifting technique is again applied, and the key K′ is left shifted by 25 bits. This process continues to obtain 96 bits in each round.
 The output transformation stage also needs four sub-keys of 16 bits each. Notice that after the eighth round, the key gets exhausted. Thus, the key is left shifted by 25 bits, and the bits 1 to 64 of the newly created key are used to generate four sub-keys (
The output transformation stage also needs four sub-keys of 16 bits each. Notice that after the eighth round, the key gets exhausted. Thus, the key is left shifted by 25 bits, and the bits 1 to 64 of the newly created key are used to generate four sub-keys (K49 to K52) for this stage.
11. Explain Advanced Encryption Standard.
Ans.: The Advanced Encryption Standard (AES) is the latest and, potentially, the most secure encryption method published by NIST. It is a symmetric-key block cipher that was designed to be a significant improvement over DES/3-DES. In 1990s, the US government decided to standardize the cryptographic algorithm and to name it as AES. In response to this, a lot of proposals were submitted. After long debates, in 2000, the US government chose one of the proposals, the Rijndael algorithm, as AES. This algorithm is named on the surnames of the two Belgian researchers Vincent Rijmen and John Daemen. Finally, in 2001, AES was published as Federal Information Processing Standard (FIPS) 197 by NIST.
General Design of AES
AES is a non-Feistel cipher that operates on a data block of 128 bits (16 bytes) and comprises several rounds for encryption and decryption. It is available in three versions, depending on the key size and the number of rounds used. These versions include AES-128 with key size 128 bits and 10 rounds, AES-192 with key size 192 bits and 12 rounds and AES-256 with key size 256 bits and 14 rounds. Despite the fact that each version uses a different key size, the round keys used in each version are always 128 bits long, which is the same size as that of the plaintext or ciphertext block. In AES, the round keys are generated using the key-expansion algorithm (explained in the next question), and the number of round keys generated is always equal to the number of rounds plus one. Figure 4.7 shows the general design for AES encryption algorithm (referred to as the AES cipher); the design of AES decryption algorithm (referred to as the AES inverse cipher) is also similar, except that the round keys are used in the reverse order from that of encryption.

Figure 4.7 General Design of AES Encryption Cipher
Each round in AES consists of many stages, each of which transforms the 16-byte data block. In AES, the term ‘data block’ is used at the beginning and end of the cipher, while before and after each
stage, the term ‘state’ is used to refer to a data block. A state, like a data block, is also 16-bytes long and contains the data before and after the transformation. Usually, a 16-byte state (say, S) is organized as a 4×4 bytes matrix, and each element of the matrix is referred to as Si,j (0≤i≤3 and 0≤j≤3), where i and j denote the row number and column number, respectively.
Structure of Encryption Round
During encryption, each round, excluding the last one, involves four transformations, namely: Substitute Bytes, Shift Rows, Mix Columns and Add Round Key (see Figure 4.8). Each transformation accepts a state, changes it and creates a new state that is given as input to the next transformation or the next round. The last round in AES comprises only three transformations, except the Mix Columns transformation. Moreover, one Add Round Key transformation is applied before the first round (mentioned as pre-round transformation in Figure 4.7). Each transformation in AES is invertible in nature and, during decryption, the inverse of these transformations, namely, Inverse Substitute Bytes, Inverse Shift Rows, Inverse Mix Columns and Add Round Key (which is self-invertible), are used. Figure 4.8 shows the general structure of an encryption round in AES.

Figure 4.8 General Structure of an Encryption Round
Transformations
All the transformations performed during encryption and decryption fall under four broad categories that include substitution, permutation, mixing and key adding. These transformations are described as follows:
 Substitution: As with DES, AES also performs the substitution of bytes, but using a different mechanism. In AES, substitution is performed for all bytes, and that too, using only one table. This implies that if 2 bytes are the same then their transformations are also same, which is contrastive to DES where eight different S-boxes perform transformations. Moreover, the bytes are substituted either with the help of a transformation table or by performing the mathematical calculations in GF(28) field. The two invertible transformations that fall under this category are as follows:
Substitution: As with DES, AES also performs the substitution of bytes, but using a different mechanism. In AES, substitution is performed for all bytes, and that too, using only one table. This implies that if 2 bytes are the same then their transformations are also same, which is contrastive to DES where eight different S-boxes perform transformations. Moreover, the bytes are substituted either with the help of a transformation table or by performing the mathematical calculations in GF(28) field. The two invertible transformations that fall under this category are as follows:
 Substitute Bytes: It is the first transformation of a round used during encryption. The input to this transformation is a state organized as a 4×4 matrix of bytes. The bytes in the matrix are substituted one at a time. Thus, there are 16 distinct byte-to-byte transformations. To substitute the bytes using a transformation table, each byte is treated as two hexadecimal digits, where the first digit (left one) specifies the row and the second digit (right one) specifies the column of the substitution table. The value (two hexadecimal digits) at the intersection of the row and the column in the transformation table is the new byte with which the given byte is to be replaced.
Substitute Bytes: It is the first transformation of a round used during encryption. The input to this transformation is a state organized as a 4×4 matrix of bytes. The bytes in the matrix are substituted one at a time. Thus, there are 16 distinct byte-to-byte transformations. To substitute the bytes using a transformation table, each byte is treated as two hexadecimal digits, where the first digit (left one) specifies the row and the second digit (right one) specifies the column of the substitution table. The value (two hexadecimal digits) at the intersection of the row and the column in the transformation table is the new byte with which the given byte is to be replaced.
 Inverse Substitute Bytes: It is used at the decryption side and is the inverse of the Substitute Bytes transformation.
Inverse Substitute Bytes: It is used at the decryption side and is the inverse of the Substitute Bytes transformation.
 Permutation: AES also permutes the bytes. It performs a byte-level permutation (unlike DES, which works on the bit level), such that the order of bits in each byte does not change in the resultant bytes. The two invertible transformations that fall under this category are as follows:
Permutation: AES also permutes the bytes. It performs a byte-level permutation (unlike DES, which works on the bit level), such that the order of bits in each byte does not change in the resultant bytes. The two invertible transformations that fall under this category are as follows:
 Shift Rows: It is used at the encryption side. In this transformation, the bytes in the rows of the input state matrix are shifted to the left, and the number of bytes to be shifted depends on the row number. For example, the row 0 is not shifted at all, the row 1 is shifted 1 byte, row 2 is shifted 2 bytes and row 3 is shifted 3 bytes.
Shift Rows: It is used at the encryption side. In this transformation, the bytes in the rows of the input state matrix are shifted to the left, and the number of bytes to be shifted depends on the row number. For example, the row 0 is not shifted at all, the row 1 is shifted 1 byte, row 2 is shifted 2 bytes and row 3 is shifted 3 bytes.
 Inverse Shift Rows: It is used at the decryption side and is similar to the Shift Rows transformation, except that here the bytes in the rows are shifted to the right.
Inverse Shift Rows: It is used at the decryption side and is similar to the Shift Rows transformation, except that here the bytes in the rows are shifted to the right.
 Mixing: The Substitute Bytes transformation is an intrabyte transformation as it transforms the bytes but does not affect the bits inside the bytes. It also does not take into account the neighbouring bytes. Similarly, the Shift Rows transformation permutes only the bytes but not the bits inside the bytes and, thus, is referred to as a byte-exchange transformation. In contrast, the Mixing is an interbyte transformation in which the bits inside the bytes are changed on the basis of bits in the neighbouring bytes. Mixing transformation takes 4 bytes at a time and combines these bytes to make 4 new bytes. In the combination process, each byte is first -multiplied with a different constant and, then, all the 4 bytes are mixed. For mixing, matrix multiplication is used. AES specifies the following two invertible transformations that fall under this category:
Mixing: The Substitute Bytes transformation is an intrabyte transformation as it transforms the bytes but does not affect the bits inside the bytes. It also does not take into account the neighbouring bytes. Similarly, the Shift Rows transformation permutes only the bytes but not the bits inside the bytes and, thus, is referred to as a byte-exchange transformation. In contrast, the Mixing is an interbyte transformation in which the bits inside the bytes are changed on the basis of bits in the neighbouring bytes. Mixing transformation takes 4 bytes at a time and combines these bytes to make 4 new bytes. In the combination process, each byte is first -multiplied with a different constant and, then, all the 4 bytes are mixed. For mixing, matrix multiplication is used. AES specifies the following two invertible transformations that fall under this category:
 Mix Columns: It is used at the encryption side. This is a column-level transformation that takes one column of input state matrix at a time and transforms it to a new column. For transforming the columns, a constant square matrix is used. The square matrix is multiplied by each column of state matrix resulting into a column. Notice that the bytes multiplication operation is performed in GF(28) field and the bytes addition operation is performed by simply XORing the bits within bytes.
Mix Columns: It is used at the encryption side. This is a column-level transformation that takes one column of input state matrix at a time and transforms it to a new column. For transforming the columns, a constant square matrix is used. The square matrix is multiplied by each column of state matrix resulting into a column. Notice that the bytes multiplication operation is performed in GF(28) field and the bytes addition operation is performed by simply XORing the bits within bytes.
 Inverse Mix Columns: It is used at the decryption side and is similar to Mix Columns transformation except that it uses the inverse of the constant square matrix used in Mix Columns transformation.
Inverse Mix Columns: It is used at the decryption side and is similar to Mix Columns transformation except that it uses the inverse of the constant square matrix used in Mix Columns transformation.
 Key adding: This is the only transformation that makes use of the round key (generated from cipher key) and, thus, is considered an important transformation. To perform key adding transformation, the 128-bit round key is considered as four 32-bit words, and further, each 32-bit word is treated as a column matrix. A self-invertible transformation that falls under this category is as follows:
Key adding: This is the only transformation that makes use of the round key (generated from cipher key) and, thus, is considered an important transformation. To perform key adding transformation, the 128-bit round key is considered as four 32-bit words, and further, each 32-bit word is treated as a column matrix. A self-invertible transformation that falls under this category is as follows:
 Add Round Key: Like Mix Columns transformation, it also operates on one column at a time; however, it uses matrix addition operation rather than matrix multiplication. Each column of the state matrix is XORed with the corresponding key word (column matrix) to produce the new column. This transformation is used in both encryption and decryption.
Add Round Key: Like Mix Columns transformation, it also operates on one column at a time; however, it uses matrix addition operation rather than matrix multiplication. Each column of the state matrix is XORed with the corresponding key word (column matrix) to produce the new column. This transformation is used in both encryption and decryption.
12. What do you mean by key expansion in AES? Explain the key expansion process in AES-128.
Ans.: Key expansion is a process used in AES to generate the round keys from the given cipher key. In AES, the number of round keys generated by this process is always one greater than the number
of rounds. That is, if there are n rounds, the key expansion generates (n+1) keys (say, K0 to Kn), out of which the first round key K0 is used in the Add Round Key transformation before the first round, and the remaining keys (K1 to Kn) are used in the corresponding rounds. In addition, the key expansion generates each round key word-by-word, where each word is an array of 4 bytes. Thus, the total number of words created in n rounds is equal to 4(n+1), denoted as d0, d1,…, d4(n+1)-1.
Key Expansion in AES-128
In AES-128, there are 10 rounds, and the cipher key is 128 bits long. Therefore, the number of keys generated is 11 (K0 to K10), and the number of words created is 44 (d0 to d43). The cipher key of 128 bits is treated as an array of 16 bytes (say, r0 to r15) – that is, four 32-bit words. Before we describe the steps involved in key expansion, we need to know the two routines, RotWord() and SubWord(), as well as round constant RCon, which are used in the process.

RotWord(): The RotWord (which stands for rotate word) routine performs a similar function as that of the Shift Rows transformation, with the exception that it is applied to only one row. It takes a 4-byte word, and shifts each byte of the word to the left with wrapping.

SubWord(): The SubWord (which stands for substitute word) routine performs a similar function as that of the Substitute Bytes transformation, with the exception that it is applied to only 4 bytes (that is, a single word). It takes each byte of a 4-byte word and substitutes it with another byte with the help of transformation table.

RCon: RCon (which stands for round constants) is a 4-byte value where the leftmost byte is non-zero and the rightmost 3 bytes are always zero. As the name implies, this value is fixed for each round. Table 4.2 lists the round constants for 10 rounds of AES-128.
| Round | RCon |
|---|---|
| 1 | (01 00 00 00 00)16 |
| 2 | (02 00 00 00 00)16 |
| 3 | (04 00 00 00 00)16 |
| 4 | (08 00 00 00 00)16 |
| 5 | (10 00 00 00 00)16 |
| 6 | (20 00 00 00 00)16 |
| 7 | (40 00 00 00 00)16 |
| 8 | (80 00 00 00 00)16 |
| 9 | (1B 00 00 00 00)16 |
| 10 | (36 00 00 00 00)16 |
The steps involved in creating 44 words (d0 to d43) from the original cipher key of 16 bytes (r0 to r15) are as follows (see Figure 4.9):
1. The 16 bytes of the cipher key (that is, r0 to r15) form the first four words d0, d1, d2 and d3. That is, d0: = r0r1r2r3, d1: = r4r5r6r7, d2: = r8r9r10r11 and d3: = r12r13r14r15.
2. Create the remaining 40 words using the following process.
for ( i = 4 to 43)do
{
if ( i mod 4)= 0 then
{
s : = SubWord(RotWord( d i-1 ))
ti: = s  RConi/4
di : = ti
RConi/4
di : = ti  di-4
}
else
di: = di-1
di-4
}
else
di: = di-1  di-4
}
di-4
}

Figure 4.9 Key Expansion in AES-128
13. How is the key expansion in AES-192 and AES-256 different from that in AES-128?
Ans.: AES-192 and AES-256 employ a similar key expansion as that of AES-128, however, with a few differences. In AES-192, the cipher key is 192 bits long and is treated as an array of 24 bytes (r0 to r23), that is, six 32-bit words. As there are 12 rounds, the key expansion creates 52 words of round key (d0 to d51), and these words are generated in groups of six. The differences between key expansion in AES-192 and AES-128 are as follows:
1. The 24 bytes of cipher key (that is, r0 to r23) form the first six words (d0 to d5) of the round key.
2. For the remaining words (di, i = 6 to 51), if (i mod 6)= 0 then di: = ti ; else,  di-6
di-6di: = di-1 . di-6
di-6
On the other hand, in AES-256, the cipher key is 256 bits long and is treated as an array of 32 bytes (r0 to r31), that is, eight 32-bit words. As there are 14 rounds, the key expansion creates 60 words of
round key (d0 to d59) and these words are generated in the groups of eight. The differences between key expansion process in AES-256 and AES-128 are as follows:
1. The 32 bytes of the cipher key (that is, r0 to r31) form the first eight words (d0 to d7) of the round key.
2. For the remaining words (di, i = 8 to 59)

if (i mod 8)= 0 then di: = ti  di-8; else, di: = di-1
di-8; else, di: = di-1  di-8.
di-8.

if (i mod 4)= 0, but (i mod 8)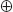 0, then di: = SubWord(di-1)
0, then di: = SubWord(di-1) 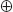 di-8.
di-8.
14. What do you mean by mode of operation in block ciphers? Explain block cipher modes of operation.
Ans.: Modern block ciphers such as DES and AES perform symmetric-key encipherment, thus providing data security. Both DES and AES have been devised to encipher/decipher fixed-size blocks of 64 and 128 bits, respectively. However, in real-life applications, the data to be enciphered is generally of variable size. Thus, some technique is needed to enhance the strength of block ciphers such as DES and AES and to adapt them to such applications so that data of any size can be enciphered. Such technique is referred to as the mode of operation. There are four commonly used block cipher modes of operations that have been suggested by NIST. These modes are discussed in the following sections.
Electronic Code Book (ECB) Mode
This is the simplest mode of operation in which the entire plaintext message is divided into m blocks (P1, P2,…, Pm), with each block containing n (usually n = 64) bits. While breaking the message, if the last block contains less than n bits, padding is used to make it equal to the other blocks.
During encryption, one n-bit block of plaintext (say, Pi) is taken at a time and encrypted using a key K to produce the corresponding n-bit ciphertext block (say, Ci). Each block is encrypted independently of the other blocks, and the same key (say, K) is used for encrypting all the blocks. During decryption also, one block is decrypted at a time, and the same key K is used for decrypting the blocks. Figure 4.10 shows the encryption and decryption processes in the ECB mode.

Figure 4.10 Encryption and Decryption in the ECB Mode
In the ECB mode, since all blocks are encrypted independent of each other, a bit error in one block during transmission will not affect any other block; however, it may cause errors in many bits within the same block. In addition, as the same key is used for encrypting all the blocks, if an n-bit block repeats in the plaintext message, the corresponding ciphertext block also repeats in the ciphertext. That is, two same plaintext blocks always result in the same ciphertext blocks. This makes the ECB mode suitable for sending only short messages, such as an encryption key, for example. For long messages, this mode may not be secure, as there are more chances of repetition in long messages.
Cipher Block Chaining (CBC) Mode
This mode of operation overcomes the problem of the ECB mode by ensuring that the same plaintext blocks will not result in the same ciphertext blocks. For this, in the CBC mode, a plaintext block is encrypted based on the previous ciphertext block. In other words, each ciphertext block depends on the corresponding current plaintext block, as well as on all the previous plaintext blocks. Like the ECB mode, the same key (say, K) is used for encrypting all the blocks.
During encryption, each plaintext block (except the first one) is first XORed with the previous ciphertext block, and then encrypted. As there is no ciphertext block prior to the first block, a data block called initialization vector (IV) is used for this. The value of this vector is randomly generated and is agreed upon by the sender and the receiver. During decryption, each ciphertext block is first decrypted using the same key (K) that was used for encryption, and then the decrypted result is XORed with the previous ciphertext block to obtain the corresponding plaintext block. In case of the first ciphertext block, the output of the decryption algorithm is XORed with IV, as used in the encryption process. Figure 4.11 shows the encryption and decryption processes in the CBC mode.

Figure 4.11 Encryption and Decryption in the CBC Mode
Cipher Feedback (CFB) Mode
The block ciphers including DES and AES operate on 64 and 128 blocks of data, respectively, and thus, are not suitable for character-oriented applications where we need to encrypt/decrypt the smaller units (say, 8 bits) at a time. In such situations, stream ciphers prove useful. The CFB is the mode that enables converting DES (or AES) into a stream cipher. As with the CBC mode, the CFB mode also uses an initialization vector (IV) that consists of 64 bits. The contents of IV are stored in the shift register. To understand how the CFB mode works, consider that d bits are to be encrypted/decrypted at a time. The following steps are used during encryption (see Figure 4.12):
1. Encrypt IV, which is stored in the shift register using the block cipher such as DES with key K, to produce an encrypted IV.
2. Take the r leftmost bits of encrypted IV and XOR them with r bits of the plaintext to be encrypted, thus producing an r-bit ciphertext (say, C). Send the ciphertext C to the receiver.
3. Shift the contents of IV stored in the shift register left by r positions, and fill the rightmost r positions with r bits of C.
4. Repeat steps 1 to 3 until the whole plaintext message is encrypted.

Figure 4.12 Encryption in the CFB Mode
During decryption, the same process is used, except that now the XOR operation is performed on the received ciphertext and the output of encryption algorithm to produce the plaintext. It should be noted that the encryption algorithm, and not the decryption algorithm, is used during decryption also.
Output Feedback (OFB) Mode
This mode is similar to the CFB mode, except that in this mode, instead of feeding ciphertext as an input to the shift register in the next stage of the encryption process, the output of IV encryption (that is, encrypted IV) is fed into the shift register. Thus, the ciphertext does not take any part in the encryption process. Figure 4.13 shows the encryption process in the OFB mode.

Figure 4.13 Encryption in the OFB Mode
An advantage of the OFB mode is that bit errors are not propagated. This means that if a bit error occurs in the ciphertext during transmission, then only the corresponding plaintext bit will be erroneous, rather than the whole message. However, an attacker can simultaneously make changes to the ciphertext and checksum of the message in a controlled way. Thus, there is no way to detect this change.
Multiple-choice Questions
1. There are _________ encryption rounds in IDEA.
(a) 5
(b) 16
(c) 10
(d) 8
2. DES encrypts/decrypts blocks of _________ bits.
(a) 128
(b) 64
(c) 56
(d) 192
3. The algorithm in the AES cipher was actually given by _________.
(a) Rijndael
(b) IDEA
(c) Blowfish
(d) None of these
4. Which of the following modes of operations does not make use of an initialization vector?
(a) Cipher block chaining
(b) Output feedback
(c) Cipher feedback
(d) Electronic codebook
5. Each round in DES uses _________ S-boxes.
(a) Five
(b) Ten
(c) Eight
(d) Six
6. Which of the following services is based on the IDEA algorithm?
(a) PGP
(b) S/MIME
(c) SET
(d) SSL
7. Which of the following transformations belong to permutation?
(a) Inverse sub-bytes
(b) Shift Rows
(c) Add Round Key
(d) All of these
8. The key expansion in AES-256 creates _________ words.
(a) 44
(b) 52
(c) 60
(d) 54
Answers
1. (d)
2. (b)
3. (a)
4. (d)
5. (c)
6. (a)
7. (b)
8. (c)
1. What are prime numbers and relatively prime numbers?
Ans.: Any positive integer greater than 1 is a prime number if and only if it is divisible by only two integers, 1 and itself. For example, the numbers 2, 3, 5, 7, 11, 13, 17 and 19 are all prime numbers, whereas the numbers 4, 6, 8 and 10 are composite (means not prime), because they have more than two divisors.
Two positive integers a and b are said to be relatively prime, or co-prime, if gcd(a, b)= 1. In other words, two numbers are said to be relatively prime if they have no common factors except the integer 1. For example, the integers 14 and 15 are relatively prime; however, the integers 14 and 16 are not relatively prime because they have a common factor other than the integer 1. Note that the integer 1 is relatively prime with any integer. Also, if n is a prime number, all integers ranging from 1 to n-1 are relatively prime to n.
2. State and prove Fermat's theorem.
Ans.: Fermat's theorem, also called Fermat's little theorem, plays an important role in public-key cryptography. The theorem states that if p is a prime number and x is a positive integer not divisible by p, then:
xp-1 ≡ 1 (mod p)
In other words, we can say that:
xp-1 mod p = 1
Proof
Consider a set of integers Zp={1, 2,…, p-1} where each element of Zp is relatively prime to p.
If all elements of Zp are multiplied by x, and the result is mapped to Zp using modular arithmetic, we get another set (say, S), as shown here:
S = {x mod p, 2x mod p,…, (p-1)x mod p}
As x is not divisible by p, none of the elements of S is zero. Also, no two elements of S are equal. Thus, we can say that the set S contains the elements of Zp, that is, {1, 2,…, p-1} in some order. On multiplying the elements in both the sets and taking the result modulo p, we get:
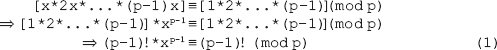
As p and (p-1) are relatively prime, the term (p-1)! can be cancelled out from both sides. Thus, equation (1) becomes:
xp-1 ≡ 1 (mod p)
Hence, proved.
There is another version of Fermat's theorem which states that, if p is a prime number and x is a positive integer, then:
xp ≡ x (mod p)
3. Explain Euler's totient function.
Ans.: Euler's totient function, also called Euler's phi function [denoted as Φ(n)], has an important role in cryptography. The value of this function is the number of positive integers that are smaller than n and relatively prime to n. The set of these numbers is represented by Zn.
A set of rules is to be followed while calculating the value of Φ(n) in the set Zn. These rules are as follows:
Rule 1: Φ(1)= 1
Rule 2: Φ(p)= p-1, if p is a prime number
Rule 3: Φ(m * n)= Φ(m)* Φ(n), if m and n are relatively prime
Rule 4: Φ(pe)= pe-pe-1, if p is prime
To compute Φ(n), suppose that we have two prime numbers p and q, such that p ≠ q and n = pq. Thus, we can write:
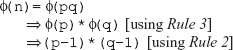
For example, for n = 21
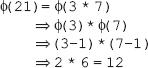
From the preceding example, it is clear that there are 12 integers that are smaller than the number 21 and relatively prime to 21.
4. State and prove Euler's theorem with the help of an example.
Ans.: Euler's theorem is also known as Fermat-Euler theorem or Euler's totient theorem. This theorem has two forms. The first form of Euler's theorem states that for every positive integer x that is relatively prime to n,
xΦ(n) ≡ 1(mod n)
Proof
If n is a prime number, then Φ(n)= n-1. Thus, the preceding equation becomes xn-1 ≡ 1(mod n), which is true by the Fermat's theorem, discussed in Question 2. Now, consider the case when n is not prime.
Let us consider a set R = {a1, a2, …, aΦ(n)}, where each ai is less than n and relatively prime to n. Multiplying each element of the set R by x and taking the result mod n, we get another set S, as shown here:
S = {(xa1 mod n),(xa2 mod n),…,(xaΦ(n) mod n)}
The set S is a permutation of R, because of the following reasons:
 As
As ai and x are relatively prime to n, xai must also be relatively prime to n. Thus, all the elements of S are positive integers that are less than n and relatively prime to n.
 The set
The set S does not contain any duplicate elements. That is, if xai mod n = xaj mod n, then ai = aj.
Therefore, we can write that:
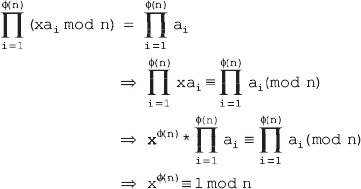
Hence, proved.
The alternative form of Euler's theorem states that:
xΦ(n)+1 ≡ x mod n
Unlike the first form, this form does not require x be relatively prime to n.
5. What is primality testing? What are its categories?
Ans.: In cryptographic algorithms, we often need to create large prime numbers. The selection of such numbers is a very challenging task. Thus, an algorithm is needed that can efficiently check whether a given large number is prime or composite. That is, we need an algorithm that can efficiently perform primality test on numbers. The algorithms for checking the primality are divided into two categories: deterministic and probabilistic.
 Deterministic algorithms: As the name suggests, these algorithms determine whether a given number is prime or not. They accept a number (say,
Deterministic algorithms: As the name suggests, these algorithms determine whether a given number is prime or not. They accept a number (say, p) as input and output the result, either that p is prime or that p is composite. There are two types of deterministic algorithms, which are as follows:
 Basic algorithm: A simple way to check whether a number
Basic algorithm: A simple way to check whether a number p is prime or not is to divide p by all values m (from 2 to p-1) and check whether p is fully divisible by any value of m. If so, then p is composite; else, it is prime.
 Divisibility algorithm: In this algorithm, instead of testing up to
Divisibility algorithm: In this algorithm, instead of testing up to p-1, testing up to only √p is sufficient. The reason behind this is that if p is composite, then it can be factored into two values, and at least one of the values must be less than or equal to √p. Thus, if the number p is divisible by any of the prime numbers less than √p, then it is composite.
 Probabilistic algorithms: As the name suggests, these tests are based on the probability theory and are used to check the probability of a number being prime. These algorithms are also referred to as randomized algorithms. They accept an integer
Probabilistic algorithms: As the name suggests, these tests are based on the probability theory and are used to check the probability of a number being prime. These algorithms are also referred to as randomized algorithms. They accept an integer p and output the probability of p being prime. There are two types of tests based on the probability theory.
 Fermat's primality test: This is a probabilistic test that checks whether a number is prime or not. We check the probability of the Fermat's little theorem to be true or false. As we know that the theorem states that if
Fermat's primality test: This is a probabilistic test that checks whether a number is prime or not. We check the probability of the Fermat's little theorem to be true or false. As we know that the theorem states that if p is prime and x is relatively prime to p such that 1 < x < p ε Zp, then:
xp-1 ≡ 1 (mod p)
To test whether p is prime or not, we pick a random number x from Zp and check whether equality holds. If equality does not hold, then p is composite, whereas if equality holds for many values of x, then p is said to be probably prime or pseudoprime. Usually, it is not possible to check the equality for all values of x. In case we pick such a value of x for which the equality holds, but p is composite, then x is known as a Fermat liar. In contrast, if we do pick a value for x such that the equality fails and p is also composite, then x is known as Fermat witness for the compositeness of p.
 Miller-Rabin test: It is also a probabilistic test to check whether a number taken at random is prime or not. This test returns the result as composite if
Miller-Rabin test: It is also a probabilistic test to check whether a number taken at random is prime or not. This test returns the result as composite if p is not prime, or as inconclusive if p may or may not be a prime number. We check the probability of the number being composite or inconclusive with the help of an algorithm given by Miller and Rabin.
6. Give the Miller-Rabin algorithm for testing primality.
Ans.: The Miller-Rabin algorithm (also known as the Rabin-Miller test) is used to test a large number for primality. It is a polynomial-time algorithm with a run-time complexity of O((log n)3).
As we know, a positive odd integer p can be written in the power of 2 as follows:
p-1 = 2kq
Where, q is an odd number that is obtained by dividing (p-1) by 2, and k is the number of times and k > 0.
For example, let p = 37. Then, p-1 = 36, which can be written as 36 = 22 * 9. Here, 9 is obtained when 36 is divided twice by 2.
In Miller-Rabin algorithm, we take into account two basic properties of prime numbers, which are as follows.
1. If p is a prime number and x is a positive integer (1 < x < p), then x2 mod p = 1 if and only if x mod p = 1 or x mod p = -1. As in modular arithmetic, -1 mod p =(p-1); therefore, x mod p = -1 means x mod p =(p-1). As we know, (x mod p)*(x mod p)= x2 mod p. Hence, whether x mod p = 1 or x mod p = -1, we always get x2 mod p = 1.
2. If p is a prime number greater than 2, we can say that p-1 = 2kq where k > 0 and q is odd, then any one of the following conditions is true:

xq mod p = 1 or xq ≡ 1 (mod p)
 One of the numbers from(
One of the numbers from(xq, x2q, x4q,…, x2(k-1)q, x2kq) is congruent to -1 modulo p. This implies that there is some j in the range(1 ≤ j ≤ k)such that:
x2(j-1)q mod p = -1 or x2(j-1)q mod p = p-1.
After considering these two properties, we can come to the conclusion that a number p can be prime if either the first element of the list (xq, x2q,x4q,…, x2(k-1)q, x2kq) modulo p is equal to 1 or if some element in this list (say, x2(j-1)q) modulo p is equal to p-1. If neither of the conditions is satisfied, the number p is not prime (that is, it is composite).
Here, it is important to note that if the condition is satisfied, it does not necessarily mean that p is prime. That is, even if the condition is satisfied, p may or may not be prime. For example, let p = 2047. Then p-1, that is, 2046, can be written as 2 * 1023, yielding k = 1 and q = 1023. Now, as 21023 mod 2047 = 1, 2047 should be prime; however, it is not. Thus, it is clear that even though a number may satisfy a condition, it may not be prime.
Miller-Rabin algorithm
Let p be an integer to be checked for primality. The algorithm returns the result as composite if p is not prime and inconclusive if p may or may not be a prime number.
1. Find integers k and q where k > 0 and q is odd such that (p-1 = 2kq).
2. Choose a random integer x such that 1< x < p-1
3. S:= xq mod p
4. If S = 1, then print (‘inconclusive’)and exit
5. for j = 0 to k-1
{
S:= x2jq mod p //equivalent to S:= S2 mod p
if S = p-1
print(‘inconclusive’)and exit
}
6. print(‘composite’)
7. Describe and illustrate the Chinese Remainder Theorem.
Ans.: Chinese Remainder Theorem (CRT) is so named as it was discovered by the Chinese mathematician Sun-Tsu in around 100 AD. It is used to solve a set of congruent equations with a single variable but different moduli, which are relatively prime. Consider such a set of equations as shown here:
a = x1 mod m1
a = x2 mod m2
.
.
.
a = xk mod mk
All these equations have a unique solution if the moduli for the equations are pair-wise relatively prime, that is, gcd(mi, mj) = 1. In case the moduli are not relatively prime but satisfy other conditions, then even we can have the solution. In cryptography, we prefer to solve the equations with relatively prime moduli.
The solution to the set of simultaneous equations can be obtained by performing the following steps:
1. Find the common modulus, M = m1* m2*…* mk.
2. Find M1 = M/m1, M2 = M/m2,…, Mk = M/mk.
3. Find the multiplicative inverse of M1, M2,…, Mk using the corresponding moduli m1, m2,…, mk. Let the inverses be M1-1, M2-1,…, Mk-1.
4. The solution to the simultaneous equations is:
a =(x1 * M1 * M1-1 + x2 * M2 * M2-1 +…+ xk * Mk * Mk-1) mod M
8. Define the following terms:
(a) Finite multiplicative group
(b) Order of the group
(c) Order of an element
(d) Primitive roots of a group
(e) Cyclic group
Ans.: (a) Finite multiplicative group: A finite multiplicative group is often used in cryptography. It is represented as G = <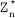 , *>
, *>
Where:
G = finite multiplicative group
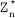
1 and n-1 that are relatively prime to n
* = the multiplication operation
The identity element (e) of the finite multiplicative group G is equal to 1.
(b) Order of the group: As we know, the order of a group is the number of elements in the group. For a finite multiplicative group G = <, the order of the group is 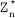 , *>
, *>Φ(n), where Φ(n) is the Euler's totient function.
(c) Order of an element: For a finite multiplicative group G = <, the order of an element (say, 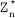 , *>
, *>a), represented as Ord(a), is the smallest integer i such that ai ≡ e(mod n), where e is the identity element of the group G. Here, the value of e is 1.
(d) Primitive roots of a group: For a finite multiplicative group G = <, the primitive roots are the elements that have the order equal to 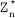 ,*>
,*>Φ(n). The number of primitive roots in a group is equal to Φ(Φ(n)).
(e) Cyclic group: If a finite multiplicative group G = < has primitive roots, it is called a cyclic group. Each primitive root of the cyclic group can be used to generate the elements of the set 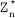 , *>
, *>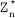
x is a generator, then elements can be created using xa modulo n, where a is an integer ranging from 1 to Φ(n), as shown here:
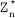 ={x1 mod n, x2 mod n, x3 mod n,…, xΦ(n) mod n}
={x1 mod n, x2 mod n, x3 mod n,…, xΦ(n) mod n}
Notice that a finite multiplicative group G = < is always cyclic if 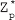 , *>
, *>p is a prime number.
9. Write a short note on discrete logarithmic problems.
Ans.: In cryptography, exponentiation and modular logarithm are often used. Exponentiation and logarithm are reverse of each other. Whenever exponentiation is used to encrypt the plaintext or decrypt the ciphertext, the opponent can use logarithm to attack. Thus, it is required to identify how difficult it is to reverse the exponentiation. An approach to determine this is to use the concept of discrete logarithm.
Consider a finite multiplicative group G = <, where 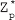 , *>
, *>p is prime. The elements of this group are the integers from 1 to p-1. In addition, the group is cyclic, as p is prime and thus has primitive roots. The primitive roots of such a group can be considered as the base of the logarithm. Thus, in case the group has m primitive roots, the calculation can be performed in m different bases.
Let us consider a as a primitive root of group G. Then, an element (say, y) of 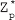
y = ax mod p
Where, x is an integer ranging from 1 to Φ(p) (which is p-1, in this case). Suppose we are given the value of y, and we are to find the value of x. Such type of problem is referred to as a discrete logarithmic problem, and the solution to this problem is given as:
x = logay mod p
That is, we need to find the log of y in base a, and then take the result mod p.
10. Find out the result of 312 mod 11.
Ans.: We can write:
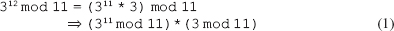
Now, according to second version of Fermat's theorem, xp ≡ x(mod p)or xp mod p = x. Thus, we get (311 mod 11)= 3. Also, (3 mod 11)= 3. Putting both these values in equation (1), we have:
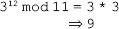
11. Find out the result of 512 mod 13.
Ans.: We can write:
512 mod 13 = 513-1 mod 13
Now, according to Fermat's theorem for a prime number p, which states that xp-1 mod p = 1, we have:
513-1 mod 13 = 1, as 13 is a prime number.
12. Find Φ(7).
Ans.: As 7 is a prime number, according to Rule 2 of the Euler's totient function [f(n)= n-1], we have:
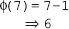
This implies that there are six positive integers that are less than 7 and relatively prime to 7. These integers include 1, 2, 3, 4, 5 and 6.
13. Find Φ(10).
Ans.: The integer 10 is a multiple of 5 and 2, therefore, we can write:
Φ(10)= Φ(5*2)
As 5 and 2 are relatively prime, by applying Rule 3 of Euler's totient function [Φ(m * n)= Φ(m)* Φ(n)], we can write:
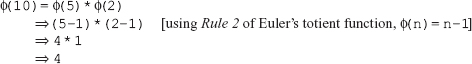
14. Check whether 89 is a prime.
Ans.: To check 89 for primeness, we can apply the divisibility test, where we check whether 89 is divisible by any of the prime numbers less than √89. Now, the integral value of √89 is 9 and the prime numbers less than 9 are {2, 3, 5, 7}. As 89 is not divisible by any of these numbers, it is a prime.
15. Apply Miller-Rabin's algorithm and use base 2 to test whether the number 561 passes the test.
Ans.: Using Miller-Rabin algorithm, explained in Question 6, we can test the number 561 as follows:

As for no value of j, S is equal to 560. Thus, 561 is composite.
16. Solve the following simultaneous congruence using Chinese Remainder Theorem to find the value of a.
a ≡ 2 mod 3
a ≡ 3 mod 5
a ≡ 2 mod 7
Ans.: Applying Chinese Remainder Theorem, explained in Question 7, the solution to the given equations is obtained as follows:
Step 1: Given m1 = 3, m2 = 5, m3 = 7
Thus, the common modulus, M = 3*5*7 = 105
Step 2: Compute M1, M2 and M3.
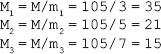
Step 3: Compute the multiplicative inverse of M1, M2 and M3 in modulo m1, m2 and m3, respectively.
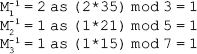
Step 4: The solution to the simultaneous equations is as follows:
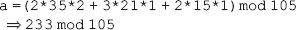
Thus, the value of a is 23.
17. Find the order of all the elements in G = <. Also find the primitive roots in the group  ,*>
,*>G.
Ans.: For the group G = <, the set  , *>
, *> contains those integers between 1 and 6 that are relatively prime to 7. That is,
contains those integers between 1 and 6 that are relatively prime to 7. That is,  = {1, 2, 3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6}= Φ(7)= 6.
For each element a of the set 
i (from 1 to 6), the condition ai ≡ 1(mod n), that is, ai mod n = 1, holds true. That value of i will be the order of the element.
1. For a = 1,
11 mod 7 = 1
Thus, the order of element 1, that is, Ord(1)= 1.
2. For a = 2,
21 mod 7 = 2 ≠ 1
22 mod 7 = 4 mod 7 = 4 ≠ 1
23 mod 7 = 8 mod 7 = 1
Thus, the order of element 2, that is, Ord(2)= 3.
3. For a = 3,
31 mod 7 = 3 ≠ 1
32 mod 7 = 9 mod 7 = 2 ≠ 1
33 mod 7 = 27 mod 7 = 6 ≠ 1
34 mod 7 = 81 mod 7 = 4 ≠ 1
35 mod 7 = 243 mod 7 = 5 ≠ 1
36 mod 7 = 729 mod 7 = 1
Thus, the order of element 3, that is, Ord(3)= 6.
4. For a = 4,
41 mod 7 = 4 mod 7 = 4 ≠ 1
42 mod 7 = 16 mod 7 = 2 ≠ 1
43 mod 7 = 64 mod 7 = 1
Thus, the order of element 4, that is, Ord(4)= 3.
5. For a = 5
51 mod 7 = 5 ≠ 1
52 mod 7 = 25 mod 7 = 4 ≠ 1
53 mod 7 = 125 mod 7 = 6 ≠ 1
54 mod 7 = 625 mod 7 = 2 ≠ 1
55 mod 7 = 3125 mod 7 = 3 ≠ 1
56 mod 7 = 15625 mod 7 = 1
Thus, the order of element 5, that is, Ord(5)= 6.
6. For a = 6,
61 mod 7 = 6 ≠ 1
62 mod 7 = 36 mod 7 = 1
Thus, the order of element 6, that is, Ord(6)= 2.
Only the elements 3 and 5 have the order equal to Φ(7), that is, 6, and therefore the primitive roots of the group G are 3 and 5.
18. Find the value of x in the group G =(for the following cases with the help of the given table. ,*)
,*)
(a) 4 ≡ 3x mod 7
(b) 6 ≡ 5x mod 7

Ans.: For the group G =( and  ,*), Φ(7)= 6
,*), Φ(7)= 6 ={1, 2, 3, 4, 5, 6}
={1, 2, 3, 4, 5, 6}a = bx mod n. These equations can be solved using the table for each 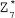
(a) 4 ≡ 3x mod 7
Here, a = 4. Thus, x = log34 mod 7
From the given table, it is clear that log34 = 4. Therefore,
x = 4 mod 7
 4
4
(b) 6 ≡ 5x mod 7
Here, a = 5. Thus, x = log56 mod 7
From the given table, it is clear that log56 = 3. Therefore,
x = 3 mod 7
 3
3
Multiple-choice Questions
1. What is the value of Φ(1)?
(a) Zero
(b) One
(c) Not defined
(d) None of these
2. The gcd of 14 and 15 is __________.
(a) One
(b) Two
(c) Three
(d) Four
3. Two positive integers a and b are said to be relatively prime if __________.
(a) Their gcd is 1
(b) They have no common prime factors
(c) If 1 is their only common divisor
(d) All of these
4. Which of the following is used for testing primality?
(a) Fermat's primality test
(b) Miller-Rabin
(c) Divisibility test
(d) All of these
5. Chinese remainder theorem is given by __________
(a) Fermat
(b) Euler
(c) Sun-Tsu
(d) Miller and Rabin
6. The number of primitive roots in a group is computed by __________
(a) Φ(Φ(n))
(b) Φ(n)
(c) Ord(n)
(d) None of these
Answers
1. (b)
2. (a)
3. (d)
4. (d)
5. (c)
6. (a)
1. What are the requirements of asymmetric-key cryptography?
Or
What are the characteristics that an asymmetric-key cryptographic algorithm must possess?
Ans.: Asymmetric-key cryptography requires the use of two different keys: the public key for encryption and private key for decryption. The public key is known to everyone, whereas the private key is known to its owner only. Diffie and Hellman laid out some requirements that must be fulfilled by the algorithms used for asymmetric-key cryptography. These requirements are listed below:
 It should be easy for the receiver to generate the pair of keys (public and private).
It should be easy for the receiver to generate the pair of keys (public and private).
 It should be easy for the sender to generate the ciphertext from the original message (that is, the plaintext) with the help of the receiver's public key.
It should be easy for the sender to generate the ciphertext from the original message (that is, the plaintext) with the help of the receiver's public key.
 It should be easy for the receiver to decrypt the ciphertext generated by the sender by using its private key in order to recover the original message.
It should be easy for the receiver to decrypt the ciphertext generated by the sender by using its private key in order to recover the original message.
 It should be infeasible for an intruder to determine the private key of the receiver, even if he or she knows the public key of the receiver.
It should be infeasible for an intruder to determine the private key of the receiver, even if he or she knows the public key of the receiver.
 It should be infeasible for an intruder to determine the original message even if he or she knows the public key of the receiver as well as the ciphertext.
It should be infeasible for an intruder to determine the original message even if he or she knows the public key of the receiver as well as the ciphertext.
 It should be possible to use any of the two keys (public or private) for encryption and decryption. That is, it should be possible to encrypt the message with any one of the keys and decrypt it using the other.
It should be possible to use any of the two keys (public or private) for encryption and decryption. That is, it should be possible to encrypt the message with any one of the keys and decrypt it using the other.
2. Explain the RSA cryptosystem.
Ans.: In 1978, a group at MIT discovered a strong method for public-key encryption. It is known as RSA, the name derived from the initials of its three discoverers Ron Rivest, Adi Shamir, and Len Adleman. RSA cryptosystem is the most widely accepted asymmetric-key algorithm; in fact, most of the practically implemented security systems are based on RSA. The algorithm requires keys of at least 1024 bits for good security. This algorithm is based on some principles from number theory, which states that determining the prime factors of a large number is extremely difficult.
RSA Key Generation
Let A and B be two users who wish to communicate. Suppose that A wants to send a message securely to B. To encrypt the message, A needs to know B's public key. Thus, B uses the following steps to generate his or her public and private keys.
1. Choose two large distinct prime numbers, p and q (about 1024 bits), such that p ≠ q.
2. n: = p*q
3. Φ(n): =(p-1)*(q-1)
4. Choose a number E such that 1 < E < Φ(n), and such that E is relatively prime to Φ(n). The public (encryption) key is (E, n), which is announced publicly.
5. Find another number D such that E * D = 1 mod Φ(n), that is, D = E-1 mod Φ(n). In other words, D is the inverse of E modulo Φ(n). The private (decryption) key is D, which is kept secret.
An important property of RSA algorithm is that the roles of E and D can be interchanged. As the number theory suggests, it is very hard to find the prime factors of a large number n, and hence it is extremely difficult for an intruder to determine the private key D using just E and n.
RSA Encryption and Decryption
In RSA, modular exponentiation is used for performing encryption and decryption. For example, if A has to send a message to B using B's public key (E, n), A encrypts the plaintext (P) to produce the ciphertext (C), as shown here:
C = PE mod n
After B has received the ciphertext (C), he or she decrypts the ciphertext using its private key (D) to get back the original plaintext (P) as shown here.
P = CD mod n
3. Discuss the different attacks on RSA.
Ans.: Although RSA is a secure algorithm used for encryption in public-key cryptography, there are still some weaknesses that enable an attacker to crack the security of the algorithm. There are several attacks that have been predicted on the basis of weak plaintext, parameter selection or inappropriate implementation. These attacks are discussed as follows:
 Factorization attack: This attack is possible if the value of
Factorization attack: This attack is possible if the value of n is small, so that the intruders can easily factorize n and obtain the value of p and q (as n = p × q). As the value of e is public, it may further result in obtaining the value of Φ(n) and d (as d = e-1 mod (p-1)(q-1)). Thus, by using all these values, an intruder can now decrypt any encrypted plaintext and crack the security. To prevent such an attack, n must be more than 300 decimal digits, so that it becomes infeasible to factorize such a long value of n.
 Chosen-ciphertext attack: This attack tries to get the plaintext from the ciphertext by using the multiplicative property of RSA. Suppose the sender sends the ciphertext (
Chosen-ciphertext attack: This attack tries to get the plaintext from the ciphertext by using the multiplicative property of RSA. Suppose the sender sends the ciphertext (C) to the receiver and an intruder intercepts it. Now, the intruder sends fake ciphertext, say Y, to the receiver by choosing a random integer X. As the receiver is unaware about the interception of the original ciphertext, he or she decrypts the fake ciphertext by performing Yd mod n to get Z. Thus, an intruder can now easily get the plaintext (P), as P = Z * X-1 mod n. That is, an intruder needs to find only the multiplicative inverse of X to get the original plaintext. Therefore, the name of attack is chosen-ciphertext attack, as only the particular ciphertext was chosen to know the corresponding plaintext.
 Timing attack: This is a cipher-text-only attack that was unveiled by Paul Kocher. In this attack, an intruder determine a private key by keeping track of how long a computer takes to decrypt the encrypted plaintext. That is, variable timing in evaluation helps an intruder find the value of each bit in
Timing attack: This is a cipher-text-only attack that was unveiled by Paul Kocher. In this attack, an intruder determine a private key by keeping track of how long a computer takes to decrypt the encrypted plaintext. That is, variable timing in evaluation helps an intruder find the value of each bit in d. This means that an intruder can now perform bit-by-bit analysis of the exponential. Such an attack can be prevented if random delays are added to exponentiation, such that the underlying hardware takes a random amount of time to process each. In addition, the concept of blinding can also be used. In this concept, the ciphertext is multiplied by a random number before evaluation. Thus, an intruder will be unable to decipher the ciphertext bits and, therefore, bit-by-bit analysis can be prevented.
 Plaintext attack: In this attack, an intruder already knows something about the plaintext. This helps the intruder to also know about the fact that the ciphertext is the permutation of the plaintext. Thus, an intruder can now compute all the possible messages until the result is equal to the ciphertext intercepted.
Plaintext attack: In this attack, an intruder already knows something about the plaintext. This helps the intruder to also know about the fact that the ciphertext is the permutation of the plaintext. Thus, an intruder can now compute all the possible messages until the result is equal to the ciphertext intercepted.
 Common modulus attack: In this attack, a common modulus is used by a group of people. That is, a whole group agrees for a trusted third party to select the values of two prime numbers
Common modulus attack: In this attack, a common modulus is used by a group of people. That is, a whole group agrees for a trusted third party to select the values of two prime numbers p and q, computes n and Φ(n) and then creates exponents (ei ,di) for each person belonging to the group. By doing this, any person who is a member of the group can decrypt the ciphertext by factoring n and can also compute the receiver's private exponent (dr) . Therefore, to prevent such attack, the modulus must not be shared, and each person in the group must calculate his or her own modulus.
4. Discuss the uses of public-key cryptography in relation to key distribution.
Ans.: One of the major problems in secret-key cryptography is that of key distribution, which can be overcome by the use of public-key cryptography. The two aspects that must be taken into account for using public-key cryptography include the distribution of public keys and the use of public-key encryption for the distribution of secret keys.
Distribution of Public Keys
There are several schemes that have been used for the distribution of public keys. These schemes are as follows:
 Public announcement: The main focus of public-key encryption is on the fact that the public key should be public; that is, a user can send his or her public key to any other user or broadcast it to a large community. Though this approach is convenient, it has some drawbacks. The main problem is that of forgery. That is, anyone can forge the key while it is being transmitted. For example, someone could pretend to be user
Public announcement: The main focus of public-key encryption is on the fact that the public key should be public; that is, a user can send his or her public key to any other user or broadcast it to a large community. Though this approach is convenient, it has some drawbacks. The main problem is that of forgery. That is, anyone can forge the key while it is being transmitted. For example, someone could pretend to be user A and send a public key to another user or broadcast it to many users. Until the original user A comes to know about this forgery and alerts other users, the forger is able to read all the messages intended for user A.
 Public directory: As the public announcement scheme for the distribution of public keys was not too secure and there were chances of forgery, a new scheme was introduced, in which a dynamic directory having the name and public key entry for each user is maintained and distributed by some trusted authority. This approach assumes that the public key of the authority is known to everyone, however the corresponding private key is known only to the authority. Each user has to register his or her public key with the directory authority. The authority either publishes the entire directory periodically in a widely circulated newspaper, or the user can access the directory electronically. The user can replace its existing key with a new one as per his or her choice. Although this scheme is more secure than public announcement, it has some weaknesses. If anyone is able to compute the private key of the directory authority, the person would get the authority to pass around the fake public keys and, later, may pretend to be a genuine user and eavesdrop on the messages being sent to any other user. The fake user may also read or alter the records kept by the authority.
Public directory: As the public announcement scheme for the distribution of public keys was not too secure and there were chances of forgery, a new scheme was introduced, in which a dynamic directory having the name and public key entry for each user is maintained and distributed by some trusted authority. This approach assumes that the public key of the authority is known to everyone, however the corresponding private key is known only to the authority. Each user has to register his or her public key with the directory authority. The authority either publishes the entire directory periodically in a widely circulated newspaper, or the user can access the directory electronically. The user can replace its existing key with a new one as per his or her choice. Although this scheme is more secure than public announcement, it has some weaknesses. If anyone is able to compute the private key of the directory authority, the person would get the authority to pass around the fake public keys and, later, may pretend to be a genuine user and eavesdrop on the messages being sent to any other user. The fake user may also read or alter the records kept by the authority.
 Public-key authority: In public directory scheme, if the private key of the authority is stolen, then it may result in loss of data. Thus, to achieve stronger security for public-key distribution, a tighter control needs to be provided over the distribution of public keys from the directory. In this case also, a central authority maintains the dynamic directory of the public keys of all the users. The user knows only the public key of the authority, while the corresponding private key is secret to the authority.
Public-key authority: In public directory scheme, if the private key of the authority is stolen, then it may result in loss of data. Thus, to achieve stronger security for public-key distribution, a tighter control needs to be provided over the distribution of public keys from the directory. In this case also, a central authority maintains the dynamic directory of the public keys of all the users. The user knows only the public key of the authority, while the corresponding private key is secret to the authority.
To understand how the public-key authority scheme works, consider two users A and B who wish to communicate securely. To enable communication, the following steps are used.
1. A sends a timestamped message containing a request for the current public key of B to the public-key authority.
2. The authority responds by sending A a message that is encrypted using the private key of authority (say, Pauthority ). The user A attempts to decrypt the message using the authority's public key. If the message gets decrypted, A is assured that the message has been sent by the authority itself. The message sent by the authority contains the following:

B's public key (say, PUBB), which can be used by A to send messages to B.
 The original request sent by
The original request sent by A, so that A can match the message received from the authority with its corresponding request, and also verify that the request was not altered before reaching the authority.
 The original timestamp, so that
The original timestamp, so that A can verify whether the message is a new one containing the current public key of B, or an old message containing any other public key.
3. A stores B's public key and uses it to encrypt the message destined for B containing an identifier of A (say, IA) and a nonce N1, which uniquely identifies this transaction.
4. B also follows the same method to retrieve A's public key from the authority. It stores the A's public key for future use. Now, both A and B have got the public keys of each other and, thus, may start exchange messages.
5. B sends a message to A, encrypting it with the public key of A (PUBA). The message contains A's nonce N1 as well as B's nonce N2. As the message could have been decrypted by B only, the inclusion of N1 in the message assures A that the corresponding user is B.
6. A returns N2, encrypted with B's public key (PUBB), to assure B that the corresponding user is A.
Note that the first four steps need not to be followed each time, as the users A and B can store the public keys of each other for future use. This technique is known as caching. However, the users should periodically request for fresh or new copies of the public keys.
 Public-key (or digital) certificates: A better approach where a user can exchange keys without communicating to the public-key authority is to use digital certificates—an electronic document that signifies the association between the user and his/her public key. A certificate authority, such as a government agency or some trusted institution, issues a certificate to each user, which contains a public key and the identifier of the key owner. The certificate is signed by the certificate authority. A user can present his or her public key to the authority to get the certificate. The user can then publish his or her certificate. Now, any other user wishing to get the public key can obtain the certificate and verify its validity by means of the attached trusted signature. The user can also send his or her key information to another user by transmitting the certificate. Users can easily verify that the certificate has been generated by the authority and that it is not a fake certificate. Moreover, only the certificate authority can create or update the certificates.
Public-key (or digital) certificates: A better approach where a user can exchange keys without communicating to the public-key authority is to use digital certificates—an electronic document that signifies the association between the user and his/her public key. A certificate authority, such as a government agency or some trusted institution, issues a certificate to each user, which contains a public key and the identifier of the key owner. The certificate is signed by the certificate authority. A user can present his or her public key to the authority to get the certificate. The user can then publish his or her certificate. Now, any other user wishing to get the public key can obtain the certificate and verify its validity by means of the attached trusted signature. The user can also send his or her key information to another user by transmitting the certificate. Users can easily verify that the certificate has been generated by the authority and that it is not a fake certificate. Moreover, only the certificate authority can create or update the certificates.
Distribution of Secret Keys using Public-key Cryptography
The public-key encryption can be exclusively used for providing distribution of secret keys that are to be used for conventional encryption. There are certain schemes for this, which are described as follows:
 Simple method: In this method, a session is created between the two users who wish to communicate (say,
Simple method: In this method, a session is created between the two users who wish to communicate (say, A and B). When A wants to communicate with B, he or she first creates a pair of public and private keys. Then, A transmits to B a message that contains the public key and A's identifier. B creates a secret key, encrypts it with the public key of A, and sends it to A. A recovers the secret key by decrypting the received encrypted message using his or her private key. At this point, both A and B know the secret key. After exchanging the secret key, A discards both the public and private keys, and B discards the public key. Now, both A and B can securely communicate using conventional encryption and the secret key.
The main advantage of this technique is that no keys exist before the start of the communication and none exists after the communication ends. Therefore, the risk of compromising the keys is minimal, and the communication is secure from eavesdropping. Note that the technique is well suited when the only threat is eavesdropping, as it does not provide confidentiality and assure authenticity of the message.
 Distribution with confidentiality and authentication: This method provides protection against both active and passive attacks. To prevent the transmission of the message from attacks, assuming that
Distribution with confidentiality and authentication: This method provides protection against both active and passive attacks. To prevent the transmission of the message from attacks, assuming that A and B have already exchanged their public keys by any of the earlier-discussed schemes, the following steps take place:
1. A sends a message to B, encrypted with the public key of B, say PUBB. The message contains an identifier of A (say, IA) and a nonce N1, which is used to identify this transaction uniquely.
2. B sends a message to A encrypted with the public key of A (say, PUBA). The message contains A's nonce N1 as well as B's nonce N2. Since only B could have decrypted the message sent by A, the inclusion of B's nonce in the message assures A that the corresponding user is B. Similarly, A sends B's nonce N2, encrypted with B's public key, to assure B that the corresponding user is A.
3. A chooses a secret key (say, SCRA), encrypts it with its private key (PRVA) and sends a message m, encrypted with B's public key (PUBB), as shown here:
m = EPUBB[EPRVA[SCRA]]
Encrypting the message m with B's public key ascertains that only B can read it, and encrypting the message with A's private key ascertains that only A could have sent it.
4. Now, B decrypts the message by computing DPUBA[DPRVB[m]], thus recovering the secret key. This method ensures both confidentiality and authenticity in the exchange of a secret key.
 Hybrid method: This method uses the key distribution centre (KDC), in which a secret master key is shared with each user. The role of KDC is to distribute the session secret keys, encrypted using the master key. A public-key scheme is used for the distribution of the session key. Generally, the applications in which session keys often change, the use of public-key encryption for distributing the secret session keys could degrade the overall system's performance. This is because relatively high computational efforts are required for the public-key's encryption and decryption.
Hybrid method: This method uses the key distribution centre (KDC), in which a secret master key is shared with each user. The role of KDC is to distribute the session secret keys, encrypted using the master key. A public-key scheme is used for the distribution of the session key. Generally, the applications in which session keys often change, the use of public-key encryption for distributing the secret session keys could degrade the overall system's performance. This is because relatively high computational efforts are required for the public-key's encryption and decryption.
The main advantage of this three-level hierarchy is that public-key encryption is rarely used to update the master key between a user and a KDC. Moreover, the scheme is compatible with existing KDC schemes and, thus, can be overlaid on existing schemes with minimal changes required.
5. Discuss Diffie-Hellman key exchange algorithm. Also discuss about its security.
Ans.: Diffie-Hellman key exchange is the first published public-key algorithm that was published in 1976 by Whitefield Diffie and Martin Hellman. This algorithm was devised for the exchange of secret keys between the communicating users in a secure manner. It allows two users to securely exchange a key that can be further used for encryption of messages. Notice that this algorithm can be used only for the exchange of keys, and not for encryption and decryption.
Diffie-Hellman key exchange algorithm enables two users to establish a symmetric session (secret) key without requiring the use of KDC. This is what is referred to as the symmetric-key agreement. Once both the communicating parties have agreed (exchanged) on the common secret key, then a symmetric-key encryption algorithm can be used for encryption and decryption of messages.
Diffie-Hellman algorithm
Consider two users A and B who want to communicate with each other securely over an insecure network. Initially, both A and B need to agree upon a key that is to be used for encryption and decryption of the messages. For this, they can follow the Diffie-Hellman key exchange algorithm, which is given below:
1. Select two numbers p and q by the mutual agreement of A and B, such that p is prime, q is a primitive root of p and q < p. There is no need to keep these two numbers secret.
2. A selects a random number XA (less than p), which becomes his or her private key. Then it computes its public key, YA, as shown here:
YA = qXA mod p
A sends its public key YA to B.
3. B selects a random number XB (less than p), which becomes his or her private key. Then, it computes its public key, YB, as shown here:
YB = qXB mod p
B sends its public key YB to A.
4. After exchanging the public keys, both A and B compute the common secret key(K). A generates the secret key as shown here:
K =(YB)XA mod p
B generates the secret key as shown here:
K =(YA)XB mod p
Proof of algorithm
To show that both A and B have computed the same secret key, we need to prove that the calculation of K by A and B produce the identical results.

Hence, proved.
Security of the Diffie-Hellman algorithm
In Diffie-Hellman algorithm, the private keys XA and XB are secret, while the numbers p and q and the public keys YA and YB are known to everyone. Thus, an opponent has p,q,YA and YB to work with. To determine the key using the available information, the opponent has to use the discrete logarithm. For example, if the opponent wants to find the private key of user A, then he or she has to perform the following calculation:
XA = dlogq,p(YA)
After computing XA, the opponent can compute the common secret key (K) in the same way that A computed it. Since it is difficult to compute the discrete logarithm in comparison to computing exponentials modulo a prime number, the security of the Diffie-Hellman algorithm depends on this fact. In case of large prime numbers, it is infeasible to compute the discrete logarithm and, thus, to break the security of the Diffie-Hellman algorithm.
5. List some advantages of the Diffie-Hellman algorithm.
Ans.: Some advantages of the Diffie-Hellman key exchange algorithm are as follows:
 Secret keys are generated as and when required. Thus, they need not be stored for a long time, thereby making them less vulnerable to attacks.
Secret keys are generated as and when required. Thus, they need not be stored for a long time, thereby making them less vulnerable to attacks.
 No pre-existing infrastructure is required for key exchange. The communicating parties just have to agree upon the values of global variables
No pre-existing infrastructure is required for key exchange. The communicating parties just have to agree upon the values of global variables p and q.
6. What are the limitations of the Diffie-Hellman algorithm?
Ans.: Although the Diffie-Hellman key exchange algorithm allows two communicating parties to securely exchange the key over an insecure network, there are a number of weaknesses to this algorithm, which are given below:
 It does not provide any information regarding the identities of the users exchanging the key. In other words, it does not authenticate the communicating users.
It does not provide any information regarding the identities of the users exchanging the key. In other words, it does not authenticate the communicating users.
 It is vulnerable to man-in-the-middle-attack, where a third user (say,
It is vulnerable to man-in-the-middle-attack, where a third user (say, C) pretends to be user B while communicating with A and pretends to be user A while communicating with B, thereby intercepting their messages. This attack is discussed in the next question.
 It involves a lot of computations and, thus, is subject to clogging attacks . In this attack, an opponent requests for a large number of keys, thus keeping the victim busy in doing unnecessary calculations rather than doing the real work.
It involves a lot of computations and, thus, is subject to clogging attacks . In this attack, an opponent requests for a large number of keys, thus keeping the victim busy in doing unnecessary calculations rather than doing the real work.
7. Explain the man-in-the-middle attack.
Ans.: As the Diffie-Hellman algorithm does not authenticate the users exchanging the keys, it is vulnerable to man-in-the-middle attacks, also referred to as the bucket brigade attack. To understand this attack, consider that A and B are two users who want to communicate and, thus, exchange their keys using the Diffie-Hellman algorithm. Let C be an opponent who wants to intercept the communication between A and B. Now, the man-in-the-middle attack proceeds as follows:
1. A sends a message containing its public key (YA) to B.
2. C intercepts this message, stores A's public key and sends a new message containing its public key (YC) and A's user ID to B.
3. On receiving the message, B saves the C's public key (YC) with A's user ID.
4. B sends a message containing its public key (YB) to A.
5. The opponent C intercepts this message, stores B's public key (YB) and sends a new message containing its public key (YC) and B's user ID to A.
6. On receiving the message, A saves C's public key (YC) with B's user ID.
7. A computes the secret key K1 based on its private key XA and C's public key YC as shown here:
K1 =(YC)XA mod p
8. B computes the secret key K2 based on its private key XB and C's public key YC, as shown here:
K2 =(YC)XB mod p
9. C computes K1 using its private key XC and YA and computes K2 using XC and YB as shown here:
K1 =(YA)XC mod p
K2 =(YB)XC mod p
At this point, A and B think that they have shared a common secret key; however, actually A and C have shared the key K1, whereas B and C have shared the key K2. The opponent C is now able to trap all the messages coming from A to B and B to A, without letting A and B know that their communication is shared with C. This happens in the following way:
1. A sends a message m encrypted with key K1 to B.
2. C intercepts the encrypted message and decrypts it to obtain the original message.
3. C sends either the same message (m) or a modified message (m') to B, encrypted using the key K2.
B receives the message assuming that it has come from A. A similar thing happens when B sends a message to A. This way, C comes in the middle of the communication between A and B and, therefore, the attack is named so.
8. What is the ElGamal encryption system? Explain its encryption and decryption processes.
Ans.: The ElGamal encryption system is a public-key cryptosystem based on the concept of Diffie-Hellman key agreement. It was discovered by Taher ElGamal in 1984. It is based on the discrete logarithm problem. To understand this problem, consider that p is a large prime number, q is an integer and e1 is a primitive root in the group G = <. Now, it is easy to compute  , *>
, *>e2 = e by using fast exponential algorithms. However, if  mod p
mod pe1, e2 and p are given, then it is difficult to calculate q = log(e1 * e2)mod p. This is what is known as the discrete logarithm problem. Thus, the security of ElGamal depends on the complexity of computing discrete logarithms.
The Elgamel encryption system consists of three different components, and separate algorithms are defined for them. The components are key generator, encryption algorithm and decryption algorithm.
ElGamal key generation
Suppose A and B are the communicating parties, and A wishes to send a message to B using the ElGamal encryption system. For this, A needs to know the public key of B. Thus, B uses the following steps to generate his or her private and public keys.
1. Choose a large prime number p.
2. Choose a random number q in the group G = <, that is,  ,*>
,*>1 ≤ q < p.
3. Choose a primitive root e1 in the group G = <Zp*,*>.
4. e2: = e.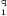 mod p
mod p
5. Announce (e1, e2, p) as the public key.
6. Retain q as the private key and keep it secret.
After knowing the public key of B, anyone can now send a message to B using its public key.
ElGamal encryption
Suppose the user A wants to send an encrypted message to B. For this, A uses the B's public key (e1, e2, p) and the following steps to convert the plaintext P to ciphertexts C1 and C2.
1. Choose a random number d in the group G = <.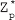 ,*>
,*>
2. C1: = e. mod p
mod p
3. C2: =(P * e.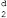 ) mod p
) mod p
4. Send C1 and C2.
ElGamal decryption
After receiving the ciphertext (C1 and C2), the recipient B uses its private key q to decrypt the ciphertext and, thus, obtain the original plaintext P, as shown here:
P =[C2(C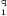 )-1] mod p
)-1] mod p
Proof of decryption
We can also verify the ElGamal decryption expression [C2(C to be equivalent to 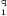 )-1] mod p
)-1] mod pP. Putting the values of C1 and C2 in the ElGamal decryption expression, we get:
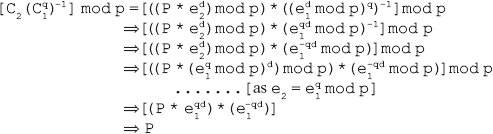
9. Discuss the different attacks on the ElGamal algorithm.
Ans.: Although the ElGamal algorithm can be used for key exchange, encryption, decryption and authentication of small messages, it has certain weaknesses that may help an attacker to crack the security of the algorithm. Generally, the ElGamal cryptosystem is subject to two types of attacks, which are as follows:
 Modulus attack: In case the value of
Modulus attack: In case the value of modulus p is small, it will be much easier for an attacker to solve the discrete logarithm problem. For example, the attacker can easily solve the discrete logarithm problem q = loge1e2 mod p and obtain the value of q. It can store the value of q and use it to decrypt any message sent to the recipient. The attacker can do so as long as the recipient uses the same keys. The attacker can also easily solve the discrete logarithm problem d = loge1C1 mod p and get the value of random number d used by the sender. Thus, to avoid this attack, it is recommended to use large values, at least of 1024 bits, for modulus p.
 Known-plaintext attack: If the sender uses the same value of
Known-plaintext attack: If the sender uses the same value of q to encrypt two different plaintexts, P1 and P2 , the attacker can determine P2 if he or she knows P1 . Let C = P1 * e and 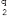 mod p
mod pC' = P2 * e. Now, the attacker can determine 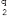 q mod p
q mod pP2 using the following steps:
1. e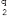 : = C' * P
: = C' * P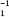 mod p
mod p
2. P2: = C' * (e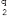 )-1 mod p
)-1 mod p
Thus, to avoid this attack, it is recommended that the sender use a different value of q to encrypt each plaintext.
10. Write a short note on elliptic curves.
Ans.: An elliptic curve can be defined by an equation in two variables with coefficients. The general form of an elliptic curve is given as:
y2 + b1xy +b2y = x3 + a1x2 +a2x +a3
Where x, y are the variables, while a1, a2, a3, b1 and b2 are the coefficients.
There are three kinds of elliptic curves, which are as follows:
 Elliptic curves over real numbers: When we talk about elliptic curves over real numbers, we use a special class of elliptic curves, of the form given here:
Elliptic curves over real numbers: When we talk about elliptic curves over real numbers, we use a special class of elliptic curves, of the form given here:
y2 = x3 + ax + b
Here, the variables x and y take values of real numbers and the coefficients a and b are the real numbers as well.
 Elliptic curves over finite field GF(p): In elliptic curves over finite field
Elliptic curves over finite field GF(p): In elliptic curves over finite field GF(p), the variables and coefficients are bound to be the elements of the finite field. Here, the elliptic curve is denoted as Ep(a,b), where p is the modulus and all calculations are made using modulo p. The elliptic curve Ep(a,b) over finite field GF(p) is represented as:
y2 mod p =(x3 + ax + b)mod p
Notice that the value of x lies between 0 and p.
 Elliptic curves over finite field
Elliptic curves over finite field GF(2n): The elliptic curves over finite field GF(2n), denoted as E2n(a,b), are of the form given here:
y2 + xy = x3 + ax2 + b
Where the variables x and y and the coefficients a and b are the elements of finite field GF(2n), and all calculations are performed in GF(2n).
11. What is the elliptic curve cryptosystem?
Ans.: The elliptic curve cryptosystem (ECC) is a public-key cryptosystem based on the theory of elliptic curves over finite field, and was unveiled by Neal Koblitz and Victor S. Miller in 1985. It involves both groups and logarithmic problems, and provides a higher rate of security at smaller key size, which is not possible using ElGamel and RSA.
In ECC, the plaintext is first encoded in the form of P(x,y) point and then further encrypted or decrypted.
ECC with Diffie-Hellman key exchange
Consider that A and B are two users who wish to communicate and, thus, exchange the secret key using ECC. The exchange of key between A and B proceeds as follows:
1. Choose a large integer p, such that p is either a prime or in the form 2n.
2. Choose the elliptic curve coefficients a and b for the cubic equations of the form y2 mod p = (x3 + ax + b)mod p or y2 + xy = x3 + ax2 + b. This defines Ep(a,b), the elliptic group of points.
3. Choose a base point G =(x1,y1) in Ep(a,b), whose order is a very large value, m.
4. A chooses an integer XA < m, which becomes his or her private key. Then, A calculates his or her public key YA, as shown here:
YA = XA * G
The public key YA is a point in Ep(a,b).
5. B chooses an integer XB < m, which becomes his or her private key. Then, B calculates his or her public key YB, as shown here:
YB = XB * G
The public key YB is a point in Ep(a,b).
6. A calculates the secret key K using his or her private key XA and the public key of B (that is, YB), as shown here:
K = XA * YB
7. Similarly, B calculates the secret key K using his or her private key XB and public key of A (that is, YA), as shown here:
K = XB * YA
Proof of algorithm
To prove that both A and B have generated the same secret key, we need to show that the calculation of K by both users yield the same result.
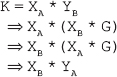
Hence, proved.
ECC encryption
When A has to send a message (say, Pm) to B, A first chooses a random integer (say, r). Then, A encrypts the message using B's public key YB and the base point G to produce the ciphertext Cm, containing the pair of points as shown here:
Cm = {r * G, Pm + r * YB}
ECC decryption
On receiving the ciphertext Cm, B decrypts the ciphertext to obtain the original plaintext Pm. For this, it multiplies the first point in Cm (that is, r * G) with its private key XB, and then subtracts it from the second point (that is, Pm + r * YB), as shown here:
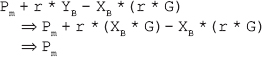
Security of ECC
A encrypts the message Pm with r * YB (r is only known to A) and r * G; therefore, the attacker needs the value of r, G and r * G to decrypt the message, which is not so easy.
12. Encrypt the plaintext 6 using RSA public key encryption algorithm. Use prime numbers 11 and 3 to compute the public key and private key. Also, decrypt the cipher text using the private key.
Ans.: According to the RSA algorithm explained in Question 2, we have:
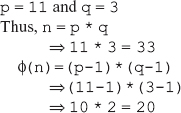
We choose D = 3 (a number relatively prime to 20, that is, gcd (20,3)= 1)
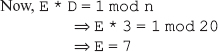
As we know, the public key consists of (E,p), and the private key consists of (D,p). Therefore, the public key is (7, 33), and the private key is (3, 33).
The plaintext 6 can be converted into ciphertext using the public key (7, 33), as shown here:

If we apply the private key to the ciphertext 30, we get the original plaintext, as follows:
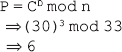
13. In the Diffie-Hellman key exchange algorithm, let the prime number be 353 and one of its primitive root be 3. Let the users A and B select their secret keys XA = 97 and XB = 233. Compute:
(i) The public keys of A and B
(ii) The common secret key
Ans.: According to the Diffie-Hellman key exchange algorithm explained in Question 5, we have:
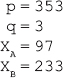
(i) Public key of A
Public key of B

(ii) Common secret key
14. A is using the ElGamal encryption system to transmit a message to B, with p = 11, primitive root in G is 2, private key of A is 3 and the plaintext is 7.
(i) Calculate e2 and public key of A
(ii) If B chooses d = 4, then calculate C1, C2
Ans.: According to the ElGamal encryption system explained in Question 8, we have:

(i) As we know, e2 = e mod p
mod p

Thus, the public key of A =(e1, e2, p)=(2, 8, 11)
(ii) Given, d = 4
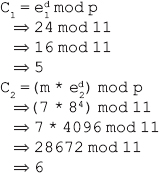
Thus, the ciphertexts are C1 = 5 and C2 = 6.
15. Using elliptic curve encryption/decryption scheme, key exchange between users A and B is accomplished. The cryptosystem parameters are elliptic group of points E11(1, 6) and point G on the elliptic curve is G = (2, 7). B's secret key is XB = 7.
(i) Find out B's public key YB.
(ii) A wishes to encrypt the message Pm = (10, 9) and chooses the random value r = 3. Determine the ciphertext Cm.
(iii) How will B recover Pm from Cm?
Ans.: Given G = (2, 7)
B's private key, XB = 7
(i) B's public key, YB, can be computed as:
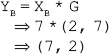
(ii) Given, Pm = (10, 9) and r = 3. Thus, the ciphertext Cm can be computed as:
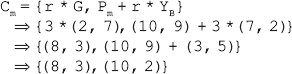
(iii) B can recover Pm from Cm using its private key (XB) as follows:
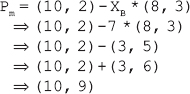
Multiple-choice Questions
1. In asymmetric-key cryptography, how many keys are required for each communicating party?
(a). 2
(b). 3
(c). 4
(d). 1
2. In asymmetric-key cryptography, the private key must be __________.
(a). Shared with anyone
(b). Distributed
(c). Kept secret
(d). None of these
3. In asymmetric-key cryptography, if A wants to communicate with B, then B must know __________.
(a). A's private key
(b). A's public key
(c). B's private key
(d). B's public key
4. If a sender encrypts the message with his or her private key, it achieves __________.
(a). Confidentiality
(b). Confidentiality and authentication
(c). Confidentiality but not authentication
(d). Authentication
5. To decrypt a message that is encrypted using RSA, we need the __________.
(a). Sender's private key
(b). Sender's public key
(c). Receiver's private key
(d). Receiver's public key
6. Which method provides a higher level of security with a small-sized key?
(a). RSA
(b). ElGamal
(c). Elliptic curve cryptography
(d). Diffie-Hellman key agreement
7. Which of the following is the first secure key exchange algorithm?
(a). RSA
(b). ElGamal
(c). Elliptic curve cryptography
(d). Diffie-Hellman key agreement
Answers
1. (a)
2. (c)
3. (b)
4. (b)
5. (c)
6. (c)
7. (d)
1. What do you mean by message authentication?
Ans.: Message authentication refers to the mechanism used to ensure that the integrity of the received message has been preserved - that the message has not been altered during transmission. It also assures the receiver that the message has originated from the intended sender and not from any intruder. Thus, a message is said to be authentic if the message has not been altered and has come from the actual sender.
2. What types of attacks are addressed by message authentication?
Ans.: The messages transmitted across a network are subject to various attacks. The types of attacks that are addressed by message authentication are as follows:
 Masquerade: This attack happens when the messages from a fraud source are put into the network; an intruder impersonates an authorized entity and creates fake messages, which are sent to the recipient. This attack also includes the fake acknowledgements corresponding to the received or failed messages by some other entity except the intended recipient.
Masquerade: This attack happens when the messages from a fraud source are put into the network; an intruder impersonates an authorized entity and creates fake messages, which are sent to the recipient. This attack also includes the fake acknowledgements corresponding to the received or failed messages by some other entity except the intended recipient.
 Modification of the message: This attack involves making certain modifications in the contents of the captured message or changing the sequence of messages being transmitted between the communicating parties. An intruder may insert, delete or transpose the contents of the message, or he or she may reorder the messages being sent in order to cause an unauthorized effect.
Modification of the message: This attack involves making certain modifications in the contents of the captured message or changing the sequence of messages being transmitted between the communicating parties. An intruder may insert, delete or transpose the contents of the message, or he or she may reorder the messages being sent in order to cause an unauthorized effect.
 Timing modification: This attack involves delaying or replaying the messages being transmitted. The term ‘replay’ means capturing a copy of the message sent by the original sender and retransmitting it later to bring about an unauthorized result. In a connection-oriented application, the entire session can be delayed or replayed, whereas in a connection-less application, the individual messages can be delayed or replayed.
Timing modification: This attack involves delaying or replaying the messages being transmitted. The term ‘replay’ means capturing a copy of the message sent by the original sender and retransmitting it later to bring about an unauthorized result. In a connection-oriented application, the entire session can be delayed or replayed, whereas in a connection-less application, the individual messages can be delayed or replayed.
3. Discuss various types of authentication functions?
Ans.: Each authentication mechanism involves the use of a function to produce a value to be used for authenticating a message. This value is known as the authenticator. The authenticator enables the recipient of the message to verify the authenticity of the message.
The authentication functions that are used to produce an authenticator fall under three classes, which are as follows:
 Message encryption: In this class, the authenticator of the message is the ciphertext that is produced after encrypting the entire plaintext.
Message encryption: In this class, the authenticator of the message is the ciphertext that is produced after encrypting the entire plaintext.
 Message authentication code (MAC): In this class, the authenticator of the message is a fixed-length value that is generated by applying a function on the message and the secret key.
Message authentication code (MAC): In this class, the authenticator of the message is a fixed-length value that is generated by applying a function on the message and the secret key.
 Hash function: In this class, a hash function (also called message digest algorithm ) is applied on a variable-length message to produce a fixed-length output that acts as the authenticator of the message.
Hash function: In this class, a hash function (also called message digest algorithm ) is applied on a variable-length message to produce a fixed-length output that acts as the authenticator of the message.
4. Write a short note on message authentication code?
Ans.: Message authentication code (MAC) is a piece of information used to authenticate a message being transmitted between two communicating parties. A MAC algorithm is applied on an arbitrary-length message to be authenticated and the common secret key shared between the parties to generate a small fixed-size block of data called cryptographic checksum (or MAC). The calculated MAC is concatenated with the original message, and the message plus MAC are then sent to the receiver.
Let A and B be two parties that share a common secret key K. When A wants to send a message (say, M) to B, it computes MAC by applying the MAC algorithm (say, C) on message M and secret key K, as shown here:
MAC = C(K, M)
After MAC has been computed, A sends the message M and MAC to B through the network. On receiving, B distinguishes the message M from MAC and applies the same MAC algorithm C on the message M and the secret key K to generate MAC'. Then, MAC' and MAC are compared to determine whether they are the same. If so, B is assured that the message M has not been altered, because if it was changed by an attacker, then MAC' would not match with MAC; the attacker cannot change MAC to correspond to the changed message, as he or she is not aware of the secret key K. In addition, B is also assured that the message M has actually come from A, since nobody else could have created a message with the proper MAC without having knowledge of the secret key K. Notice that in case the messages being transmitted between A and B also comprise sequence numbers, then B can also be assured about the proper sequence, as the attacker cannot change the sequence number successfully.
Figure 7.1 depicts the use of MAC to authenticate a message at the sender's end and to verify the authenticity of the message at the receiver's end.

Figure 7.1 Message Authentication using MAC
MAC is different from message encryption in the sense that the MAC algorithm is not required to be reversible as it should be for decryption at the receiver's end. Generally, the MAC function is a many-to-one function whose domain comprises messages of any length, while the range comprises all possible MACs and keys. For an n-bit MAC, there are 2n possible MACs and m possible messages, where m>>2n. For a k-bit key, there are 2k possible keys. For example, if the messages being transmitted are of 100 bits and the MAC is of 10 bits, then there are 2100 different messages and 210 different MACs. Thus, it can be said that, on average, each MAC is generated by 2100/210 = 290 different messages. Furthermore, if the key used is of 10 bits, then there are 210 different mappings between all the messages and the MACs.
MAC is widely helpful in some situations, which are as follows:
 When the same message has to be broadcasted to several destinations, it would be desirable to assign to one destination the responsibility of checking the authenticity of the message. Thus, the plaintext message and the message authentication code must be sent to all the destinations. Since the responsible destination is aware of the secret key, it verifies whether the message is authentic. In case some violation occurs, it alerts other destinations.
When the same message has to be broadcasted to several destinations, it would be desirable to assign to one destination the responsibility of checking the authenticity of the message. Thus, the plaintext message and the message authentication code must be sent to all the destinations. Since the responsible destination is aware of the secret key, it verifies whether the message is authentic. In case some violation occurs, it alerts other destinations.
 When the receiving side is heavily loaded and cannot decrypt all the messages, then messages can be authenticated on a selective basis. That is, the messages are chosen randomly for verification.
When the receiving side is heavily loaded and cannot decrypt all the messages, then messages can be authenticated on a selective basis. That is, the messages are chosen randomly for verification.
 When it is more important to authenticate messages rather than keeping them secret.
When it is more important to authenticate messages rather than keeping them secret.
5. Write down the purpose of hash function along with a simple hash function.
Ans.: A hash function (or one-way hash function) is a variation of MAC used for message authentication. Like MAC, it takes a variable-length message as input and produces a fixed-length output referred to as the hash code or hash value or a message digest. However, unlike MAC, a hash function does not require a secret key and, thus, is also called a non-key message digest. Formally, the hash code (h) can be expressed as:
h = H(M)
Where,
M = message (string) of any length
H = hash function
H(M) = a fixed-length string (hash code).
At the sender's end, the hash code is computed and concatenated with the message. The message plus hash code are then sent to the receiver through the network. At the receiving end, the receiver separates the message from the hash code and again applies the hash function on it to produce a new hash code. If the recomputed hash code is the same as the received hash code, the message is authenticated.
A secret key is not given as an input to hash function. Thus, hash code plays the role of a ‘signature’ for the data being sent from the sender to the receiver through the network. In addition, the hash function takes into account all bits of the message; therefore, a change to any bit of the message results in a change to the hash code.
Simple Hash Function
All the hash functions consider the input message as a sequence of blocks where each block is of m bits. They process the input message one block at a time iteratively and produce an m-bit hash code.
One of the simple hash functions takes the bitwise XOR of every block of the input message to produce the hash code. This can be expressed as follows:
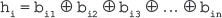
Where,
hi = ith bit of the hash code with 1 ≤ i ≤ m
n = number of m-bit blocks in the input message
bik = ith bit of the kth block with 1 ≤ k ≤ n.
The preceding operation is known as longitudinal redundancy check (LRC), and it generates a simple parity corresponding to each bit position. It effectively ensures data integrity for randomly selected input; however, it proves less effective in case of predictable formatted data. To improve the effectiveness, an alternate simple hash function is used that circular-shifts (or rotates) the hash value by one bit after processing each block. This hash function uses the following steps to produce an m-bit hash code from an input message consisting of m-bit blocks.
1. Set all the m bits of hash code to zeros.
2. For each successive m-bit block, perform the following:
i. Shift left the current value of hash code by one bit.
ii. Take the XOR of new hash code and the block.
6. What characteristics (requirements) are needed in secure hash function.
Ans.: A hash function takes as input a variable-length message, a file or any block of data and produces a hash code, referred to as the fingerprint of the message, file or block of data. If M is a variable-length message and H is the hash function, then the hash code (h) can be expressed as:
h = H(M)
The hash function must possess the following properties in order to be used for message authentication.
1. The hash function should be applicable on a block of data of any size.
2. The output produced by the hash function should always be of fixed length.
3. For any given message or block of data, it should be easier to generate the hash code. That is, given a message M, H(M) should be easily computable. This property is important to make the hardware and software implementation feasible.
4. Given a hash code, it should be nearly impossible to determine the corresponding message or block of data. That is, if h is given, one should not be able to determine M such that H(M)= h. This is referred to as one-way property. This property is of prime importance when a secret value is being used in the authentication technique. Though the secret value is not sent through the network, the attacker can still easily find out the secret value if the used hash function does not show the one-way property.
5. Given a message or block of data, it should not be computationally feasible to determine another message or block of data generating the same hash code as that of the given message or block of data. That is, if M1 is given, there is no other M2 (where M1 ≠ M2) such that H(M1)= H(M2). This property is referred to as weak collision resistance.
6. No two messages or blocks of data, even being almost similar, should be likely to have the same hash code. That is, it is virtually impossible to determine a pair (M1,M2) such that H(M1)= H(M2). This property is referred to as strong collision resistance.
From these six properties, if the first five properties are satisfied, then the hash function is called a weak hash function, and if all the six properties are satisfied, then it is called a strong hash function. This is because the sixth property protects the hash function from the birthday attack.
7. Describe the birthday attack against any hash function.
Ans.: When two different messages on applying the same hash function yield the same hash code, it is known as collision. A specific type of cryptographic attack that is performed against hash functions in order to discover collisions in them is referred to as birthday attack. This attack is based on the principle of Birthday Paradox, according to which, in a group of 23 randomly chosen people, the probability of finding two people sharing the same birthday is more than 50%. In case the number of people increases to 57, this probability becomes more than 99%. Thus, it can be concluded that the probability of finding a pair with same birthday in a group increases with increase in number of people in the group and, at a certain point, it may reach 100%.
In a birthday attack against a given hash function H, the goal of the attacker is to find two input messages, say M1 and M2, such that H(M1)= H(M2); this is what is referred to as collision. To detect the collision, the attacker may continue to evaluate the hash function H for different randomly selected inputs until he or she gets the same output more than once. In case a hash function H produces N different outputs with same probability and N is quite large, then it can be expected to get a pair of different inputs M1 and M2 such that H(M1) = H(M2) after we evaluate the function for approximately 1.25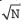 different inputs on average.
different inputs on average.
To estimate the expected number of values that we must choose before detecting the first collision, let us take q values at random from the set of N values, with repetitions allowed. Further, assume that p(q; N) denotes the probability that at least one value is chosen more than once. The approximate value of this probability can be given as shown here:
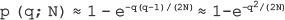
If n(p; N) denotes the least number of values that must be chosen such that the probability for detecting a collision is at least p, then we can find the approximate value of n(p; N) by inverting the preceding expression as shown here:

For 50% probability of detecting collision (that is, p = 0.5), we get
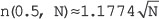
Now, the expected number of values that must be selected before detecting the first collision, denoted as Q(N), can be approximated as shown here:
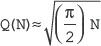
For example, if we use a 64-bit hash code, then there will be approximately 1.8 × 1019 different outputs. If all of these are equally probable (the best case), then an attacker would require approximately 5.1 × 109 attempts to generate a collision using brute force. This value is called birthday bound. In general, for an m-bit hash code, the birthday bound can be approximated as 2m/2.
8. Write a short note on iterated hash functions?
Ans.: To ensure message integrity, the hash functions are used that produce a fixed-length message digest from a variable-length message. To accomplish this efficiently, iterations are used in the hash function. In place of using hash functions with variable-length input, the hash functions with fixed-length input can also be created and used the required number of times. Such a fixed-size input hash function is termed as a compression function. This function takes as input an m-bit string and produces an n-bit string as output such that n < m. This scheme is known as iterated cryptographic hash function.
There are two different approaches that can be used in designing iterated hash functions. In the first approach, the cryptographic hash functions employ a compression function that is made from the scratch and has been designed for that specific purpose. Examples of such cryptographic hash functions include all versions of message digest (MD) algorithm such as MD2, MD4 and MD5 as well as all versions of secure hash algorithm (SHA) such as SHA-1, SHA-224, SHA-256, SHA-384 and SHA-512. On the other hand, in the second approach, the cryptographic hash functions use a symmetric-key block cipher such as triple-DES or AES as the compression function. Notice that the role of block ciphers here is to perform only encryption and not decryption. An example of a cryptographic hash function based on this approach is Whirlpool.
9. Explain MD5 algorithm with the help of a block diagram.
Ans.: MD5 (message digest, version 5) is a cryptographic hash algorithm developed by Ron Rivest in 1991. It came into existence after its four predecessors, all of which were developed by Rivest. The original hash algorithm was named MD. Then came MD2, which was quite weak. Therefore, Rivest started working on MD3. However, due to some technical deficiency, MD3 was never released. This led Rivest to the release of MD4, which too worked for a short period of time and ultimately, it was replaced by MD5. MD5 is quite fast and has been resistant to collision till now.
Figure 7.2 shows the block diagram for generating message digest using MD5. The algorithm takes a variable-length message as input and produces a fixed-length message digest. It processes the given input in blocks of 512 bits, which are again divided into 16 blocks of 32 bits each. The output obtained is a set of four blocks of 32 bits each, that is, total 128 bits.

Figure 7.2 Generation of Message Digest using MD5
The following steps are involved in the working of MD5.
Step 1: Append Padding Bits
In the initial step, the padding bits are added to the end of the original message. This is done as to make the number of bits in the message equal to 64 bits less than an integral multiple of 512. For example, if the original message is of 1900 bits, then 84 bits are padded to make the length of the message 1984 bits. The reason behind adding 84 bits is that when we add 64 to 1984, we get 2048, which is an exact multiple of 512 (512*4 = 2048). Padding bits comprise a single one bit followed by the required number of zero bits. It is mandatory to add padding bits even if the length of the original message plus 64 is already an exact multiple of 512. For example, if the original message is of 448 bits (448 + 64 = 512), even then 512 padding bits need to be added. Thus, the number of padding bits may vary from 1 to 512 bits, and the length of the message after adding padding bits can be 448 bits, 960 bits, 1472 bits, and so on.
Step 2: Append Length
The next step is to calculate the length of the message excluding the padding bits. For example, if the original message is 1900 bits long, and the length of message after adding padding bits is 1984 bits, then here the length is considered as 1900 and not 1984. The length (say, L) is expressed as a 64-bit value, and these 64 bits are added at the end of the message, plus the padding bits. In case the message is too long to be expressed as a 64-bit value, then we need to take the length modulo 264. After appending the length, we get a message whose length is an exact multiple of 512. Now, the digest of this message is to be found.
Step 3: Divide the Input Message into 512-bit Blocks
In this step, the input message is divided into N 512-bit blocks, denoted as M1, M2, …, MN. For example, in our case, the 2048-bit message will be divided into four blocks of 512 bits each.
Step 4: Initialize MD Buffer
A 128-bit buffer is used to hold the intermediate and final results of the hash function while computing the message digest. This buffer is represented as four 32-bit registers (A, B, C, D). Each of these registers is initialized with a 32-bit integer in hexadecimal (initial hash values), as shown here:

The MD5 algorithm treats the registers A, B, C and D as a single 128-bit register ABCD.
Step 5: Process Blocks
Each 512-bit block of the message is now processed as follows:
a. Copy the contents of A, B, C and D into four corresponding 32-bit variables H0, H1, H2 and H3 as shown here:
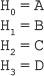
b. The 512-bit block is divided into 16 sub-blocks of 32 bits each, denoted as, S1, S2, …, S16 or in general as Si where 1 ≤ i ≤ 16.
c. Now, the compression function, labelled as HMD5 in Figure 7.2, is applied on the 512-bit block. The compression function comprises four rounds where each round takes three inputs: all the 16 32-bit sub-blocks of the current 512-bit block, the register ABCD and an array of constants T (see Figure 7.3). The array T consists of 64 elements of 32 bits each, represented as T1, T2, …, T64 or in general as Tj where 1 ≤ j ≤ 64. As there are total four rounds, 16 values of array T are used in each round. Each round updates the contents of the register ABCD by performing the MD5 algorithm steps.
d. Each round contains 16 iterations, one per each sub-block, that is, there are total 64 iterations in MD5 for one 512-bit block. Each iteration involves certain operations to update the contents of the register ABCD.
After performing all the 64 iterations for one 512-bit block, each of the four registers (A, B, C and D) is incremented by the value it had before the processing of that block, as shown here:
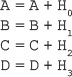
This incremented value of A, B, C and D (128 bits together) becomes one of the inputs to the first round of the next 512-bit block. Notice that addition is performed using modulo 232.

Figure 7.3 MD5 Processing of a Single 512-Block
Single MD5 Iteration: Each iteration in MD5 goes through the following steps (see Figure 7.4).
i. Apply a function F on registers B, C and D. The function F differs for each round.
ii. Add the contents of register A to the output of the previous step.
iii. Add the message sub-block Si to the output of the previous step.
iv. Add the constant Tj to the output of the previous step.
v. Perform circular left shift operation by m bits on the output of the previous step. Notice that the value of m and Tj differ for each iteration, as defined by MD5.
vi. Add the contents of register B to the output of the previous step.
vii. Store the contents of register D into a 32-bit temporary variable (say, Temp).
viii. Copy the contents of register C to register D.
ix. Copy the contents of register B to register C.
x. Copy the output of step (vi) to register B.
xi. Copy the value of variable Temp to register A.

Figure 7.4 Single MD5 Iteration
After performing these steps, we get new ABCD for the next iteration.
Mathematical representation of a single MD5 iteration can be given as:
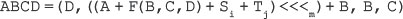
Where,
F = a non-linear function different for each round
Si = Sq x 16 + i, the ith 32-bit sub-block in the qth 512-bit block of the message
Tj = a 32-bit constant
<<<m = circular left shift by m bits
+ = addition modulo 232.
Function F: The function F is different in each of the four rounds, while the rest of the steps are the same. The function F involves some Boolean operations on the variables B, C and D in the four rounds, as shown here:

Step 6: Output
After all the 512-bit blocks of the message have been processed, the contents of the register ABCD form the 128-bit message digest.
10. Explain the working of SHA-1.
Ans.: Secure Hash Algorithm (SHA), also referred to as Secure Hash Standard (SHS), was developed by the National Security Agency (NSA). In 1993, it was published by the National Institute of Standards and Technology (NIST) as a Federal Information Processing Standard (FIPS PUB 180). In 1995, a revised version of SHA was issued as FIPS PUB 180-1, which was given the name SHA-1. SHA-1 has been designed such that it is computationally infeasible to determine the original message from a given message digest, as well as to determine two messages generating the same message digest.
Figure 7.5 shows the block diagram for generating a message digest using SHA-1. Like MD5, the SHA-1 algorithm takes an input message with a maximum length of 264 bits and processes the input in 512-bit blocks. However, it produces a message digest of 160 bits, unlike MD5.

Figure 7.5 Generation of Message Digest using SHA-1
The working of SHA-1 involves the following steps:
Step 1: Append Padding Bits
In the initial step, the padding bits are added to the end of the original message. This is done as to make the number of bits in the message equal to 64 bits less than an integral multiple of 512. For example, if the original message is of 1900 bits, then 84 bits are padded to make the length of the message 1984 bits. The reason behind adding 84 bits is that when we add 64 to 1984, we get 2048, which is an exact multiple of 512 (512*4 = 2048). Padding bits comprise a single one bit followed by the required number of zero bits. It is mandatory to add padding bits even if the length of the original message plus 64 is already an exact multiple of 512. For example, if the original message is of 448 bits (448 + 64 = 512), even then 512 padding bits need to be added. Thus, the number of padding bits may vary from 1 to 512 bits, and the length of the message after adding padding bits can be 448 bits, 960 bits, 1472 bits and so on.
Step 2: Append Length
The next step is to calculate the length of message excluding the padding bits. For example, if the original message is 1900 bits long, and the length of message after adding the padding bits is 1984 bits, then here the length is considered as 1900 and not 1984. The length (say, L) is expressed as a 64-bit value, and these 64 bits are added at the end of the message plus padding bits. In case the message is too long to be expressed as a 64-bit value, then we need to take the length modulo 264. After appending the length, we get a message whose length is an exact multiple of 512. Now, the digest of this message is to be found.
Step 3: Divide the Input Message into 512-bit Blocks
In this step, the input message is divided into N 512-bit blocks, denoted as M1, M2, …, MN. For example, in our case, the 2048-bit message will be divided into four blocks of 512 bits each.
Step 4: Initialize Hash Buffer
A 160-bit buffer is used to hold the intermediate and final results of the hash function while computing the message digest. This buffer is represented as five 32-bit registers (A, B, C, D, E). Each of these registers is initialized with a 32-bit integer in hexadecimal (initial hash values), as shown here:

The SHA-1 algorithm treats the registers A, B, C, D and E as a single 160-bit register ABCDE.
Step 5: Process Blocks
Each 512-bit block of message is now processed. Initially, the contents of the five registers A, B, C, D and E are copied to five 32-bit variables H0, H1, H2, H3 and H4, respectively. Then, the 512-bit block is divided into 16 sub-blocks of 32 bits each. Now, the compression function, labelled as HSHA-1 in Figure 7.5 , is applied on the 512-bit block. The compression function consists of four rounds, with each round consisting of 20 iterations. That is, a total of 80 iterations are performed to process one 512-block. As shown in Figure 7.6 , each of the four rounds takes three inputs: all the 16 32-bit
sub-blocks of the current 512-bit block, the register ABCDE and an additive constant Ti where 1 ≤ i ≤ 80. Unlike MD5, in SHA-1, we have only four values defined for Ti, one value per round, as shown in Table 7.1.

Figure 7.6 SHA-1 Processing of a Single 512-bit Block
| Round | Value of i | Value of Ti (in hexadecimal) |
|---|---|---|
1 |
1 ≤ i ≤ 20 |
5A 92 79 99 |
2 |
21 ≤ i ≤ 40 |
6E D9 EB A1 |
3 |
41 ≤ i ≤ 60 |
F8 1B BC DC |
4 |
61 ≤ i ≤ 80 |
CA 62 C1 D6 |
Each iteration of SHA-1 involves certain operations to update the contents of the register ABCDE. After performing all the 80 iterations for one 512-bit block, each of the five registers (A, B, C, D and E) is incremented by the value it had before the processing of that block, as shown here:
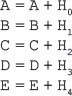
This incremented value of A, B, C, D and E (160 bits together) becomes one of the inputs to the first round of next 512-bit block. Notice that addition is performed using modulo 232.
Single SHA-1 Iteration: Each iteration in SHA-1 goes through the following steps (see Figure 7.7).
i. Apply a function F on registers B, C and D. The function F differs for each round.
ii. Add the contents of register E to the output of the previous step.
iii. Store the contents of register A into a 32-bit temporary variable (say, Temp).
iv. Perform circular left shift operation by five bits on the contents of register A.
v. Add the output of step (ii) and step (iv).
vi. Derive Wi from the current sub-block and add it to the output of the previous step.
vii. Add the constant Ti to the output of the previous step.
viii. Copy the contents of register D to register E.
ix. Copy the contents of register C to register D.
x. Perform circular left shift operation by 30 bits on the contents of register B and store the result in register C.
xi. Copy the value of variable Temp to register B.
xii. Copy the output of step (vii) to register A.

Figure 7.7 Single SHA-1 Iteration
After performing the preceding steps, we get new ABCDE for the next iteration.
Mathematical representation of a single SHA-1 operation can be given as:
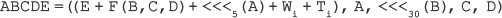
Where,
F = a non-linear function different for each round
Wi = a 32-bit block derived from current 32-bit sub-block Si based on rules (see Table 7.2)
Ti = one of the five 32-bit additive constants
<<<m = circular left shift by m positions
+ = addition modulo 232.
| Value of i | Value of Wi |
|---|---|
1 ≤ i ≤ 16 |
Same as Mi |
17 ≤ i ≤ 80 |
|
Function F: The function F is different in each of the four rounds, while the rest of the steps are the same. The function F involves some Boolean operations on the variables B, C and D in the four rounds, as shown here:
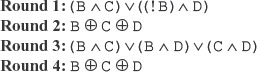
Step 6: Output
After all the 512-bit blocks of the message have been processed, the contents of the register ABCDE form the 160-bit message digest.
11. Differentiate between SHA-1 and MD5.
Ans.: Both SHA-1 and MD5 are message digest algorithms. The design and functionality of SHA-1 and MD5 are almost similar. However, there are certain key differences between them. Some of these differences are listed in the Table 7.3.
| SHA-1 Algorithm | MD5 Algorithm |
|---|---|
| It generates a message digest of 160 bits. | It generates a message digest of 128 bits. |
| It uses little-endian scheme to interpret the message as a sequence of 32-bit words. In this scheme, the most significant byte of a 32-bit word is stored in the low-address byte position. | It uses big-endian scheme, where the least significant byte of a 32-bit word is stored in the low-address byte position. |
| It undergoes four rounds, each having 20 iterations, that is, a total of 80 iterations are used. Moreover, it requires a 160-bit buffer and, thus, is slower in operation than MD5. | It undergoes four rounds, each having 16 iterations, that is, a total of 64 iterations are used. Moreover, it requires a 128-bit buffer and, thus, is faster in operation than SHA-1. |
| It requires 2160 operations for finding the original message from the given message digest and 280 operations to find two messages generating the same message digest. | It requires 2128 operations for finding the original message from the given message digest and 264 operations to find two messages generating the same message digest. |
| It is not vulnerable to cryptanalytic attack. | It is vulnerable to cryptanalytic attack. |
| It is more secure than MD5. | It is less secure as compared to SHA-1. |
12. Explain Whirlpool cryptographic hash function.
Ans.: Whirlpool is a cryptographic hash function designed by Vincent Rijmen and Paulo S.L.M. Barreto. It is one of the hash functions that have been supported by New European Schemes for Signatures, Integrity, and Encryption (NESSIE). It is based on the use of a symmetric-key block cipher instead of a compression function as used in MD5 and SHA. The Whirlpool cipher is a modified version of the Advanced Encryption Standard (AES) cipher.
Whirlpool Hash Function
Figure 7.8 shows the block diagram for generating a message digest using Whirlpool (the triangular hatch in the figure indicates key input). The algorithm takes as input a message with a maximum length of up to 2256 bits, processes the input in 512-bit blocks and returns a 512-bit hash code as output. The steps involved in the working of the Whirlpool hash function are as follows:
1. Append padding bits: In the initial step, the padding bits are added to the end of the original message. This is done so as to make the length of the message an odd multiple of 256. For example, if the original message is of 600 bits, then 168 bits are padded to make the length of the message 768 bits (768 = 256*3). Padding bits comprise a single one bit followed by the required number of zero bits. It is mandatory to add padding bits even if the length of the original message is already of the desired length. For example, if the original message is of 256 bits, even then 512 padding bits need to be added to make the length equal to 768 bits. Thus, the number of padding bits may vary from 1 to 512 bits.

Figure 7.8 Message Digest Generation using Whirlpool
2. Append length: The next step is to calculate the length of the message excluding the padding bits. The length (say, L) is expressed as a 256-bit value, and these 256 bits are added at the end of the message plus padding bits. After appending the length, we get a message whose length is an even multiple of 256 or an integral multiple of 512.
3. Divide the message into 512-bit blocks: The message is divided into N 512-bit blocks, M1, M2, …, MN. Each of these blocks is treated as an array of 8-bit bytes (that is, total 64 bytes). A byte matrix of size 8 × 8 is used to hold the intermediate and final hash values. The matrix is initialized with zero bits.
4. Process message blocks: Each message block of 512 bits is processed through the Whirlpool cipher (W) and, finally, a 512-bit message digest (h) is generated. To process the first message block, the 512-bit message digest (h0) is initialized with all zeros and is used as the cipher key for encrypting the first message block. The ciphertext produced after encrypting each block is XORed with the previous cipher key and previous plaintext block. The result obtained is used as the cipher key for encrypting the next 512-bit block. This process continues, and the final ciphertext block after the last XOR operation becomes the final 512-bit message digest h.
Whirlpool Cipher
The Whirlpool cipher (W) is a non-Feistel cipher that operates on 512-bit blocks (64 bytes). It consists of 10 rounds and uses a key size of 512 bits. The cipher uses a total of 11 round keys (K0, K1, …, K10), with each key of 512 bits. The round keys are generated using the key expansion algorithm. The general design of the Whirlpool cipher is shown in Figure 7.9.

Figure 7.9 General Design of Whirlpool Cipher
State and blocks: Each round in the Whirlpool cipher consists of many stages, where each stage transforms the 512-bit (64-byte) data block. As with AES, the Whirlpool cipher also uses the term ‘block’ at the beginning and end of the cipher and the term ‘state’ before and after each stage. The only difference is that here the size of state and block is 512 bits. Each 512-bit block is treated as a row matrix of 64 bytes, and a state is treated as a square matrix of 8 × 8 bytes. The transformation from block to state and vice versa is performed row wise, unlike in AES cipher.
Structure of each round: Each round involves four transformations; namely, Substitute Bytes, Shift Columns, Mix Rows and Add Round Key (see Figure 7.10). Moreover, one Add Round Key transformation is applied before the first round (mentioned as pre-round transformation in Figure 7.9). Each transformation accepts a state, changes it and creates a new state, which is given as input to the next transformation or the next round.

Figure 7.10 Structure of each Round in Whirlpool Cipher
The transformations involved in each round are described as follows:
 Substitute Bytes: This is the first transformation of a round that performs substitution of bytes. The input to this transformation is an 8 × 8 byte state matrix. The bytes in the matrix are substituted one at a time; thus, there are 64 distinct byte-to-byte transformations. The bytes are substituted either with the help of a substitution table or by performing the mathematical calculations in
Substitute Bytes: This is the first transformation of a round that performs substitution of bytes. The input to this transformation is an 8 × 8 byte state matrix. The bytes in the matrix are substituted one at a time; thus, there are 64 distinct byte-to-byte transformations. The bytes are substituted either with the help of a substitution table or by performing the mathematical calculations in GF(24) field. To substitute the bytes using a substitution table, each byte is treated as two hexadecimal digits, where the first digit (left one) specifies the row and the second digit (right one) specifies the column of the substitution table. The value (two hexadecimal digits) at the intersection of the row and the column in the substitution table is the new byte with which the given byte is to be replaced. Notice that, in this transformation, the contents of each byte is changed; however, the order of bytes in the matrix does not change.
 Shift Columns: This transformation performs the byte-level permutation. It is similar to Shift Rows transformation of AES with the only difference that, here, the columns of the matrix are shifted, and not the rows. The bytes in the columns of the input state matrix are shifted to the left and the number of the bytes to be shifted depends on the column number. For example, the column 0 is not shifted at all, the column 1 is shifted one byte, column 2 is shifted two bytes, and so on.
Shift Columns: This transformation performs the byte-level permutation. It is similar to Shift Rows transformation of AES with the only difference that, here, the columns of the matrix are shifted, and not the rows. The bytes in the columns of the input state matrix are shifted to the left and the number of the bytes to be shifted depends on the column number. For example, the column 0 is not shifted at all, the column 1 is shifted one byte, column 2 is shifted two bytes, and so on.
 Mix Rows: This is a matrix transformation that diffuses the bits inside the bytes of the state matrix. It takes one row of input state matrix at a time and transforms it to a new row. For transforming the rows, a constant square matrix is used whose each row is the circular right shift of its previous row. The square matrix is multiplied by each row of the state matrix, resulting in another row. Notice that the bytes multiplication operation is performed in the
Mix Rows: This is a matrix transformation that diffuses the bits inside the bytes of the state matrix. It takes one row of input state matrix at a time and transforms it to a new row. For transforming the rows, a constant square matrix is used whose each row is the circular right shift of its previous row. The square matrix is multiplied by each row of the state matrix, resulting in another row. Notice that the bytes multiplication operation is performed in the GF(28) field, and the bytes addition operation is performed by simply XORing the bits within bytes.
 Add Round Key: This is the only transformation that makes use of the round key. To perform this transformation, the 512-bit round key is considered as an 8 × 8 state matrix. Each byte of the input state matrix is added with the corresponding byte of round key state matrix in the GF(28 ) field, resulting in a new byte.
Add Round Key: This is the only transformation that makes use of the round key. To perform this transformation, the 512-bit round key is considered as an 8 × 8 state matrix. Each byte of the input state matrix is added with the corresponding byte of round key state matrix in the GF(28 ) field, resulting in a new byte.
13. What is HMAC? What are its design objectives? Explain its working.
Ans.: Hash-based MAC (HMAC) is a message authentication code derived from a cryptographic hash function such as MD5 and SHA-1. The basic idea behind HMAC is to use a secret key in the existing message digest algorithms (hash functions). It has been issued as a standard (FIPS 198) by NIST. As algorithms such as MD5 and SHA-1 do not rely on the secret key, HMAC has been selected as mandatory-to-implement MAC for IP security. It is also used in other Internet protocols, such as Secure Socket Layer (SSL).
HMAC can work with any existing message digest algorithms (hash functions). It considers the message digest produced by the embedded hash function as a black box. It then uses the shared symmetric key to encrypt the message digest, thus, producing the final output, that is, MAC.
Design Objectives of HMAC
HMAC was issued as RFC 2104, which defines the following objectives for HMAC.
 To use the existing hash functions such as MD5 and SHA-1 without modification.
To use the existing hash functions such as MD5 and SHA-1 without modification.
 To be able to easily replace an existing hash function in case a fast hash function is available or needed.
To be able to easily replace an existing hash function in case a fast hash function is available or needed.
 To maintain the original performance of the function till the time it is possible.
To maintain the original performance of the function till the time it is possible.
 To use the keys and to handle them in a simple and efficient manner.
To use the keys and to handle them in a simple and efficient manner.
 To better understand the cryptographic analysis of the strength of the authentication mechanism used in embedded hash function.
To better understand the cryptographic analysis of the strength of the authentication mechanism used in embedded hash function.
HMAC Implementation
The implementation of HMAC is very complex. Before discussing the algorithm, let us define the variables used in the algorithm.
H = embedded cryptographic hash function such as MD5 or SHA
IV = initial value to the hash function
M = input message
q = number of input blocks in M
n = length of the message digest (or hash value)
b = number of bits in a block
Mi = ith block of input message with 1 ≤ i ≤ q
K = shared symmetric key (secret key)
Kpad = secret key K padded with 0s on the left to make the length b bits
Ipad = input pad, a constant having value 00110110 (36 in hex) repeated b/8 times
Opad = output pad, a constant having value 01011100 (5C in hex) repeated b/8 times
Mathematically, the HMAC operation can be expressed as:
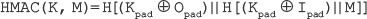
Figure 7.11 depicts the HMAC operation. Initially, the given input message M is divided into q blocks, M1, M2, …, Mq, with each block having b bits. Then, the following steps are performed to produce the n-bit message digest.
1. Add padding bits to secret key K: Add the required number of zeros to the left of secret key K to make it a b-bit string, Kpad. It is recommended that the original size of secret key K should not be greater than n, the length of the message digest.
2. XOR Kpad with Ipad : Apply XOR operation on b-bit Kpad obtained from the previous step and the constant Ipad to create a b-bit block, say S1.
3. Append M to S1 : Append the input message M (equivalent to q b-bit blocks) to the output of the previous step, that is, S1. The result is q+1 blocks of b bits each.

Figure 7.11 HMAC Structure
4. Apply hash function: Apply the selected hash function H on the stream containing q+1 blocks, generated in the previous step, to produce n-bit digest, referred to as the intermediate HMAC. The n-bit IV is also given as input to the hash function.
5. Add padding bits to intermediate HMAC: Add the required number of zeros to the left of n-bit intermediate HMAC to produce h′ with length equal to b bits.
6. XOR Kpad with Opad: Apply XOR operation on b-bit Kpad and the constant Opad to create a b-bit block, say S2.
7. Append h′ to S2: Append the b-bit intermediate HMAC (h′) obtained from step 5 to the output of the previous step, that is, S2.
8. Apply hash function: Apply the same hash function H with an n-bit IV as input on the output of the previous step to produce a final n-bit message digest.
14. Discuss the security of HMAC.
Ans.: The security of HMAC depends on the cryptographic strength of the embedded hash function, the size of secret key used and the length of the message digest produced. In essence, the probability of attacking HMAC successfully is equal to either of the following attacks on the embedded hash function.
 The intruder can calculate the output of compression function without having the knowledge of
The intruder can calculate the output of compression function without having the knowledge of IV, which is selected at random and kept secret.
 The intruder determines the collisions in the hash function even if the I V is secret and random.
The intruder determines the collisions in the hash function even if the I V is secret and random.
To attempt the first attack, the compression function can be viewed as a hash function that is applied on a message containing only one b-bit block. The intruder selects a random value of n bits (i.e. the length of the message digest produced) and uses it in place of IV. However, to perform this attack on the hash function, either a brute-force attack on the secret key or a birthday attack is to be attempted, because HMAC involves the secret key also while computing the hash value. Attempting a brute-force attack on the secret key requires the intruder to perform 2n operations.
On the other hand, to attempt the second attack, the intruder needs to determine two messages, M1 and M2, such that when the hash function H is applied on them, they yield the same output, that is, H(M1)=H(M2). This is the birthday attack, and it requires the intruder to perform 2n/2 operations in case the hash code is of n bits. For example, if the MD5 algorithm, which produces 128-bit hash code, is used as the embedded hash function, the intruder has to perform 264 operations in order to attempt birthday attack on the hash function. Performing so many operations does not seem infeasible with today's technology. However, it does not necessarily mean that MD5 is unsuitable to HMAC. The reason behind this is explained in the following text.
The intruder can attack MD5 by selecting some set of messages and generating the corresponding hash codes to determine the collisions. As the intruder knows the hash function as well as the default IV to MD5, he or she is able to work offline on some dedicated computing facility. However, when MD5 is used in HMAC, the intruder cannot determine the messages and their corresponding hash codes offline. This is because HMAC also involves the use of a secret key that is not known to the intruder. Therefore, the intruder needs to observe a series of messages being generated by HMAC using the same key and then attempt to attack these known messages. For a 128-bit hash code in MD5, this requires observing 264 blocks generated using the same key. To observe so many blocks on a 1-Gbps link, one would need approx 1,50,000 years to succeed. Thus, the use of MD5 is acceptable to HMAC as far as speed is concerned.
Multiple-choice Questions
1. A _________ is used to verify the integrity and authenticity of a message.
(a) Decryption algorithm
(b) Message digest
(c) MAC
(d) Both (b) and (c)
2. Which of the following is the latest version of the SHA algorithm?
(a) SHA-512
(b) SHA-256
(c) SHA-128
(d) SHA-1
3. The purpose of hash function is to ensure _________.
(a) Message integrity
(b) Message authentication
(c) Both (a) and (b)
(d) None of these
4. Choose the odd one out.
(a) RC5
(b) Blowfish
(c) ECC
(d) MAC
5. When two different messages yield the same message digest, it is called _________.
(a) Attack
(b) Collision
(c) Hash
(d) None of these
6. Which of the following is based on the use of asymmetric-key block cipher?
(a) SHA-1
(b) MD5
(c) RIPEMD
(d) Whirlpool
7. An attacker needs to perform _________ operations in order to determine collision in SHA-1.
(a) 264
(b) 280
(c) 2256
(d) 272
Answers
1. (c)
2. (a)
3. (a)
4. (d)
5. (b)
6. (d)
7. (b)
1. What is digital signature? Discuss the various services it provides.
Ans.: A digital signature is an authentication mechanism that allows the sender to attach an electronic code with the message in order to ensure its authenticity and integrity. This electronic code acts as the signature of the sender and, hence, is named digital signature. Digital signatures use the public-key cryptography technique. The sender uses his or her private key and a signing algorithm to create a digital signature, and the signed document can be made public. The receiver, on the other hand, uses the public key of the sender and a verifying algorithm to verify the digital signature.
Digital signatures are analogous to physical handwritten signatures and provide the following security services.
 Message authentication: A normal message authentication scheme protects the two communicating parties against attacks from a third party (intruder). However, a secure digital signature scheme protects the two parties against each other also. Suppose
Message authentication: A normal message authentication scheme protects the two communicating parties against attacks from a third party (intruder). However, a secure digital signature scheme protects the two parties against each other also. Suppose A wants to send a signed message (message with A's digital signature) to B through a network. For this, A encrypts the message using his or her private key, which results in a signed message. The signed message is then sent through the network to B. Now, B attempts to decrypt the received message using A's public key in order to verify that the received message has really come from A. If the message gets decrypted, B can believe that the message is from A. However, if the message or the digital signature has been modified during transmission, it cannot be decrypted using A's public key. From this, B can conclude that either the message transmission has tampered with, or that the message has not been generated by A.
 Message integrity: Digital signatures also provide message integrity. If a message bears a digital signature, then any change in the message after the signature is attached will invalidate the signature. That is, it is not possible to get the same signature if the message is changed. Moreover, there is no efficient way to modify a message and its signature such that a new message with
a valid signature is produced. These days, a hash function is used in the signing and verifying algorithms that help in preserving the integrity of the message.
Message integrity: Digital signatures also provide message integrity. If a message bears a digital signature, then any change in the message after the signature is attached will invalidate the signature. That is, it is not possible to get the same signature if the message is changed. Moreover, there is no efficient way to modify a message and its signature such that a new message with
a valid signature is produced. These days, a hash function is used in the signing and verifying algorithms that help in preserving the integrity of the message.
 Nonrepudiation: Digital signatures also ensure nonrepudiation. For example, if
Nonrepudiation: Digital signatures also ensure nonrepudiation. For example, if A has sent a signed message to B, then in future A cannot deny about the sending of the message. B can keep a copy of the message along with A's signature. In case A denies, B can use A's public key to generate the original message. If the newly created message is the same as that initially sent by A, it is proved that the message has been sent by A only. In the same way, B can never create a forged message bearing A's digital signature, because only A can create his or her digital signatures with the help of that private key.
 Message confidentiality: Digital signatures do not provide message confidentiality, because anyone knowing the sender's public key can decrypt the message. Thus, to achieve message confidentiality, we need to encrypt the message along with the signature using either the secret-key encryption or public-key encryption scheme. For example, if we use the public-key encryption scheme, then at
Message confidentiality: Digital signatures do not provide message confidentiality, because anyone knowing the sender's public key can decrypt the message. Thus, to achieve message confidentiality, we need to encrypt the message along with the signature using either the secret-key encryption or public-key encryption scheme. For example, if we use the public-key encryption scheme, then at A's end, first the message is encrypted using A's private key and then a second encryption is performed using the B's public key. Similarly, at B's end, first the message is decrypted using B's private key and then a second decryption is performed using A's public key. With this mechanism, only B can decrypt the encrypted message received from A because only B knows his or her private key.
2. Describe the digital signature process with the help of a suitable diagram.
Ans.: The digital signature process is shown in Figure 8.1. Suppose user A wants to send a signed message to B through a network. To achieve this communication, these steps are followed:
(i) A uses his private key (EA), applied to a signing algorithm, to sign the message (M).
(ii) The message (M) along with A's digital signature (S) is sent to B.
(iii) On receiving the message (M) and the signature (S), B uses A's public key (DA), applied to the verifying algorithm, to verify the authenticity of the message. If the message is authentic, B accepts the message; otherwise it is rejected.
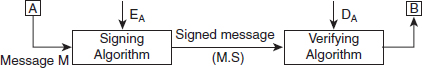
Figure 8.1 Digital Signature Process
3. How is the use of private and public keys in digital signatures different from that in public-key cryptography?
Ans.: The private and public keys used in public-key cryptography are different from the private and public keys used in digital signatures. In the former case, the public and private keys of the receiver are used for encryption and decryption of the message, respectively. That is, the sender encrypts the message using the receiver's public key, and the receiver decrypts the message using his own private key. However, in digital signatures, the private and public keys of the sender are used to create and verify the digital signature, respectively. That is, the sender creates a digital signature using his or her own private key, and the receiver verifies it using the sender's public key.
4. Can we use a secret (symmetric) key in the digital signature process? Justify your answer.
Ans.: We cannot use a secret (symmetric) key to create and verify digital signatures, due to the following two reasons.
 In symmetric-key cryptosystem, a secret key
In symmetric-key cryptosystem, a secret key K is shared between two users only, say A and B. Now, if A wants to send another message to C, then he or she has to use another secret key.

B could create a forged signed message using the secret key K that is shared between A and B, and send that message to C pretending that it has come from A.
5. What are the essential properties and requirements for a digital signature?
Ans.: A digital signature is used in those situations where there is a lack of trust between the sender and the receiver. For example, suppose a user A transfers funds to B electronically. Now, B in future increases the amount of funds transferred and claims that the larger amount had arrived from A. Thus, to achieve secure communication between the two users and to resolve their disputes if any, digital signature must have the following properties:
 It must be able to verify the author and the date and time of the signature.
It must be able to verify the author and the date and time of the signature.
 It must be able to authenticate the contents of the message at the time of the signature.
It must be able to authenticate the contents of the message at the time of the signature.
 There must be some third (trusted) party who can verify the digital signature to resolve disputes between the sender and receiver.
There must be some third (trusted) party who can verify the digital signature to resolve disputes between the sender and receiver.
Thus, we can say that the authentication function is included within the digital signature function. Based on the these properties, we can list out the following requirements for a digital signature:
 The signature must be in the form of a bit pattern and relative to the message being signed.
The signature must be in the form of a bit pattern and relative to the message being signed.
 The signature must contain some information that is unique to the sender, so that forgery and denial can be avoided.
The signature must contain some information that is unique to the sender, so that forgery and denial can be avoided.
 The process of creating the digital signature must be comparatively easy.
The process of creating the digital signature must be comparatively easy.
 The process of recognizing and verifying the digital signature must also be comparatively easy.
The process of recognizing and verifying the digital signature must also be comparatively easy.
 A high computational effort must be required to forge a digital signature. That is, it must be infeasible for an intruder to create a new message for an existing signature or to create a fake digital signature for an existing message.
A high computational effort must be required to forge a digital signature. That is, it must be infeasible for an intruder to create a new message for an existing signature or to create a fake digital signature for an existing message.
 The copy of a digital signature must be retained in some storage mechanism.
The copy of a digital signature must be retained in some storage mechanism.
6. Discuss the different kinds of attacks on digital signatures.
Ans.: There are three kinds of attacks possible on digital signatures, namely, key-only, known message and chosen-message attack. To get an idea of these attacks, consider A and B as the communicating parties and C as the opponent.
 Key-only attack: In this type of attack, the intruder knows only the public information of
Key-only attack: In this type of attack, the intruder knows only the public information of A. With the help of this information, the intruder tries to create A's digital signature. He then forges the message by putting the newly created A's signature and sends the signed message to B pretending that it has come from A. It is similar to the ciphertext-only attack discussed in Chapter 2.
 Known-message attack: In this type of attack, the intruder has access to some messages signed by
Known-message attack: In this type of attack, the intruder has access to some messages signed by A. That is, he or she already has one or more message–signature pairs. With the help of these known message–signature pairs, the intruder tries to create another message and forge A's digital signature on it. This attack is similar to the known-plaintext attack discussed in Chapter 2.
 Chosen-message attack: In this type of attack, the intruder manages to let
Chosen-message attack: In this type of attack, the intruder manages to let A sign one or more messages for him. In other words, the intruder himself chooses a message–signature pair.
Later, he creates a new message with the contents he or she wants and forges A's digital signature on it, and sends it to B pretending that it has come from A. This attack is similar to the chosen-plaintext attack discussed in Chapter 2.
7. Discuss the different approaches proposed for the digital signature function.
Ans.: A digital signature cannot be a constant and must be a function of the entire document it signs. There are several approaches that have been proposed for the digital signature function. These approaches are categorized into two types: direct and arbitrated.
Direct digital signature
In the direct digital signature approach, the signed document is directly passed from the sender to the receiver. That is, no third party is involved in carrying out this communication, because it is assumed that the receiver knows the public key of the sender and, hence, can easily verify the authenticity of the message. There are two ways of creating a digital signature—one, by encrypting the whole message with the sender's private key, and another, by taking the hash of the message and then encrypting it with the sender's private key. Message confidentiality can be achieved by further encrypting the message and the signature with the receiver's public key in case of public-key encryption or shared key in case of symmetric-key encryption.
Though there is no third party directly involved in carrying out the communication between the sender and receiver, in case of disputes, the third party may be involved in resolving the conflicts. The third party views both the message and its signature. If the signature function is applied on the encrypted message, then the third party also needs to know the decryption key to read the plaintext message. However, if the signature function is applied on the plaintext message, then the recipient can simply store the plaintext message and its signature, so that it can be used in future for resolving disputes. Thus, it is better to apply the digital signature function on the message before encrypting it.
The main problem with the direct digital signature scheme is that if the sender wants to deny the sending of a particular message, he or she can claim that his or her private key is stolen or lost and that someone has forged the signatures. Since no trusted third party is directly involved in the communication, it is difficult to verify whether the key was actually stolen, or if the sender is lying. This type of threat can be controlled to some extent by two ways:
 The sender whose key has been stolen can immediately report to a central authority, or
The sender whose key has been stolen can immediately report to a central authority, or
 The sender can include a timestamp (date and time) in each signed message.
The sender can include a timestamp (date and time) in each signed message.
The latter solution can still be compromised. For example, if the private key of the sender A is actually stolen at time (t), then some intruder (say, X) can create A's signature and send a forged signed message to B including a timestamp before or equal to t.
Arbitrated digital signature
In the arbitrated digital signature approach, a third party known as the trusted arbiter is directly involved in the process. Every signed message sent by the sender to the receiver goes through the arbiter. The arbiter performs two functions. First, it verifies the integrity (origin and content) of the signed message and signature by applying a certain number of tests. Second, it attaches the date and time of creation of the message, and forwards the message to its final destination. This scheme is based on the assumption that both the sender and receiver completely trust the arbiter's claim that he or she verifies the message to the level of his or her satisfaction and will not alter the data in any way.
The main advantages of the arbitrated digital signature approach are as follows:
 Both the communicating parties cannot share any kind of information before communication, thus preventing the chances of any kind of fraud.
Both the communicating parties cannot share any kind of information before communication, thus preventing the chances of any kind of fraud.
 Any incorrectly dated message cannot be sent to the receiver.
Any incorrectly dated message cannot be sent to the receiver.
 The contents of the message from
The contents of the message from A to B are hidden from the trusted third party and others.
8. Write a short note on the RSA digital signature scheme.
Ans.: In addition to the encryption and decryption of a message, the RSA approach can also be used for signing and verifying the message. In this case, it is known as the RSA digital signature scheme. At the sender's end, the message M to be signed is given as input to a function, which produces the digital signature S with the help of sender's private key. The sender then transmits both the message and the signature to the receiver. At the receiver's end, the digital signature S is given as input to a function, which computes the copy of the message (M′) with the help of sender's public key. Now, the receiver compares the received and the computed message. If M and M′ are congruent, the receiver accepts the message, otherwise rejects it. The RSA digital signature scheme is shown in Figure 8.2.

Figure 8.2 RSA Digital Signature Scheme
The key generation, signing and verifying algorithms for the RSA digital signature scheme are described as follows:
Key generation: The sender generates his or her private and public key as follows:
(i) The sender chooses two prime numbers p and q and computes the following:
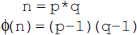
(ii) He then chooses e(1 < e < Φ(n)), the public exponent, and computes his private key d such that:
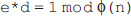
Signing: The sender creates his digital signature S using his private key d as follows:
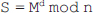
where M is the message to be signed.
Verifying: The receiver receives the message M and signature S, and computes a copy of the message using the sender's public key (e, n) as follows:
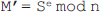
The receiver then compares M′ with M. If M′ ≡ M, the message is accepted; otherwise, it is rejected.
To prove the RSA digital signature scheme, we need to show that M′ ≡ M(mod n).
As,

And,
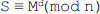
Thus, we can write equation (1) as

Hence, proved.
RSA digital signature scheme on a message digest
The RSA digital signature scheme can also be applied on a message digest. In this case, a strong hash function h is applied on the message M to create the message digest D, which is then encrypted with the sender's private key to form the digital signature S. The sender sends the message M and the signature S to the receiver. At the receiver's end, the same hash function h is applied to the received message M to compute D. The receiver also decrypts the received digital signature S with the help of the sender's public key to produce D′. Now, the receiver compares D and D′, if D is congruent to D′, the message is accepted; otherwise it is rejected.
9. Explain ElGamal digital signature scheme.
Ans.: The ElGamal digital signature scheme also consists of three different components, namely, key generation, signing and verifying. All the three components use separate algorithms. In this scheme, four functions are used, in which one function is common in both the signing and verification process, however, with different inputs. Thus, in total, only three different functions are used in the whole process.
In the signing process, two functions F1 and F2 are used to create two different digital signatures S1 and S2, respectively. The sender transmits the message M and the signatures S1 and S2 to the receiver. On receiving the message and the two signatures, the receiver computes two verification codes V1 and V2 with the help of the functions F1 and F3, respectively. Now, the receiver compares two codes V1 and V2; if both are congruent, the message is accepted; otherwise it is rejected. The ElGamal digital signature scheme is shown in Figure 8.3.

Figure 8.3 ElGamal Digital Signature Scheme
The key generation, signing and verifying algorithms for ElGamal digital signature scheme are described as follows:
Key generation: The sender generates his or her private and public keys as follows:
(i) The sender chooses a large prime number p, such that the discrete log problem is difficult in 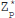 .
.
(ii) The sender then chooses his or her private key d, such that 1≤d < p−1, and computes 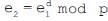 , where
, where e1 is a primitive root 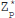 . The public key of
. The public key of A is (e1, e2, p), and the private key is d.
Signing: To create the signature, the sender chooses a random number k, such that 0 < k < q, and then computes the value of S1 and S2 as follows:
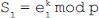
(S1 is independent of the message M)
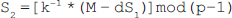
(where k−1 is the multiplicative inverse of k modulo p)
Digital signature = (S1, S2)
Verifying: The receiver verifies the signature as follows.
He or she first checks whether 0 < S1 < p and 0 < S2 < p−1, and then computes the two verification codes V1 and V2 as follows:
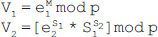
Now, the receiver tests whether V1 ≡ V2. If the condition is satisfied, the signature is accepted; else, it is rejected.
We can prove the verification as follows:

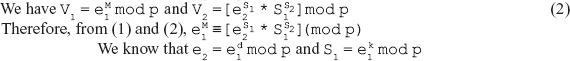
Therefore, we get:
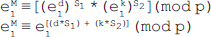
The above congruence holds if and only if:
M ≡[(d * S1) + (k * S2)]mod(p−1) or,
S2 ≡[(M−d * S1) * k−1]mod(p−1), which is same S2 as in the signing process.
10. Explain DSS, its approaches and its algorithm with proof.
Ans.: The Digital Signature Standard (DSS) was published by the National Institute of Standards and Technology (NIST) as the Federal Information Processing Standard (FIPS 186). It was originally developed in 1991. However, it was then criticized by the public because of lack of security in the scheme. Thus, it was revised in 1993, and finally in 2000, an elaborated version of DSS came into existence, which was named FIPS 186-2. The DSS uses Secure Hash Algorithm (SHA) and presents a new digital signature scheme, Digital Signature Algorithm (DSA).
As in the ElGamal digital signature scheme, in the DSS scheme also two functions F1 and F2 are used to create two different digital signatures S1 and S2, respectively. However, in DSS scheme, the message digest (not the message) is used to create the digital signature S2. The sender transmits S1, S2 and M to the receiver. On receiving the message and the two signatures, the receiver computes the message digest using the same hash function, and calculates the verification code Vc using another function F3. Now, the receiver compares Vc with S1; if both are congruent, the message is accepted; otherwise it is rejected. The DSS scheme is shown in Figure 8.4.

Figure 8.4 DSS Scheme
The key generation, signing and verifying algorithms for DSS scheme are described as follows. All the algorithms use the following global parameters:
L = length of the key in bits, where the number of bits are a multiple of 64; L lies between 512 and 1024 bits
p = prime number such that 2L-1 < p < 2L
q = a 160-bit prime factor of (p−1)
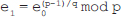 , where
, where e0 is a primitive element in Zp with 1 < e0 < p−1, such that e1 > 1
M = message to be signed
h(M) = hash of message M using the SHA algorithm
Key generation: The sender generates his or her private and public keys as follows:
 Private key: The sender chooses a random integer
Private key: The sender chooses a random integer d such that 0 < d < q; d becomes the private key of the sender
 Public key: The sender computes the following:
Public key: The sender computes the following:
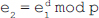
The public key of sender becomes (e1, e2, p, q)
Signing: To create the signature, the sender chooses a random number k, such that 0 < k < q, and then computes the value of S1 and S2 as follows:
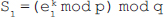
(S1 is independent of the message M)
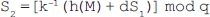
Digital signature = (S1, S2)
Verifying: The receiver verifies the signature as follows:
He or she first checks whether 0 < S1 < p and 0 < S2 < q, and then computes the digest of the message using the same hash function h(M). The receiver finally computes the verification code Vc as follows:
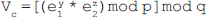
where,

(w, y and z are intermediate variables)
Now, the receiver tests whether S1 ≡ Vc. If the condition is satisfied, the signature is accepted; else, it is rejected.
Proof of the digital signature algorithm
To prove the algorithm, we have to show that Vc = S1.
As we know that:
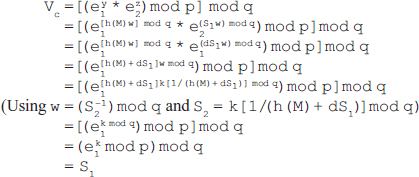
Hence, proved.
11. Why does each digital signature in the ElGamal and DSS schemes require a new value of k?
Ans.: In the ElGamal and DSS schemes, the sender chooses his or her private and public keys once and uses these keys to sign several documents. However, as we know, each time a message is sent, it should be signed with a unique digital signature; that is, no two documents can bear the same digital signature. Thus, to have a unique digital signature for every document, a new value of k (which is used in computing S1 and S2) is required.
12. How is DSS better than the RSA and ElGamal digital signature scheme?
Ans.: DSS is better than the RSA digital signature scheme because computing digital signatures in DSS requires lesser time than that in the RSA digital signature scheme for the same value of p.
DSS is also better than the ElGamal digital signature scheme because DSS scheme produces smaller digital signatures as compared to those produced by the ElGamal scheme, because q < p.
13. Explain the variations of digital signatures?
Ans.: The digital signature scheme has got many variations and additions to its main concept. Some of the variants of digital signature are discussed as follows:
 Timestamped signature: Some digital signatures include a timestamp value in order to prevent replay attacks. This is what we call timestamped signatures. In a replay attack, the documents can be replayed by a third party. For example, if
Timestamped signature: Some digital signatures include a timestamp value in order to prevent replay attacks. This is what we call timestamped signatures. In a replay attack, the documents can be replayed by a third party. For example, if A signs a request to the bank C to transfer a certain amount of money to B, B can intercept the document and replay it if there is no timestamp on the document. One way to handle such problems is to include the actual date and time. However, this may create a problem if the time zones are different or the clocks are not synchronized. Another solution is to use a nonce (which is a randomly generated number that can be used only once). The receiver makes a note that the particular nonce is used by the sender and cannot be used again. That is, a new nonce defines the present time and a used nonce defines the past time.
 Blind signature: The blind signature scheme was developed by David Chaum. The concept of blind signature is used when the sender does not want to reveal the contents of the message to the signer and just wishes get the message signed by the signer. Blind signatures are typically used in situations where the signer and the message author are completely different parties. Examples include electronic voting systems and electronic payment systems. The basic idea behind blind signatures is that the sender
Blind signature: The blind signature scheme was developed by David Chaum. The concept of blind signature is used when the sender does not want to reveal the contents of the message to the signer and just wishes get the message signed by the signer. Blind signatures are typically used in situations where the signer and the message author are completely different parties. Examples include electronic voting systems and electronic payment systems. The basic idea behind blind signatures is that the sender A first creates a message and blinds it. He then sends the blinded message to the signer B. B signs the blinded message and returns the signature on the blinded message to A. A unblinds the signature to obtain a signature on the original message.
Blind signatures scheme can be implemented by using a number of public-key digital signature schemes such as RSA and DSS. Here, we will discuss the implementation using a variation of the RSA scheme. The steps are as follows:
1. A selects a random number b, which is sometimes known as the blinding factor.
2. A calculates the blinded message as follows:
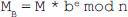
where, e = B's public key
M = original message
n = modulus defined in the RSA digital signature scheme
3. A sends MB to B.
4. B signs MB using the signing algorithm defined in the RSA digital signature scheme, as follows:
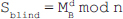
where,
Sblind = signature on the blind version of message
d = B's private key
5. A removes the blind from the signature using the multiplicative inverse of b, as follows:
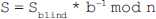
It can be easily proved that S ≡ Md (mod n); that is, the signature made on the original message M as defined in the RSA digital signature scheme. The proof is as follows:
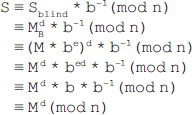
Hence, proved.
In the blind signature scheme, there are more chances of fraud. That is, it is possible that A gets a blind message signed by B that may later hurt him or her. For example, A may get a sign from B on a document that contains B's will. To deal with such type of situations, some laws have been passed that protect B in case he or she has signed a blind document that is against his or her interest.
 Undeniable digital signature: The digital signature schemes discussed so far consist of a signing algorithm and a verifying algorithm. That is, a signer can only create his or her signature using his or her private key, and anyone having the signer's public key can verify the signatures. Thus, the verification can be performed without the signer's consent or involvement. In some cases, a signer may not like it that anyone can verify his or her signatures. Thus, in order to increase the privacy of the signer, another scheme called undeniable digital signature scheme was proposed by David Chaum and Hans van Antwerpen in 1989. This scheme is a non-self-authenticating signature scheme in which no signatures can be verified without the signer's cooperation and notification.
Undeniable digital signature: The digital signature schemes discussed so far consist of a signing algorithm and a verifying algorithm. That is, a signer can only create his or her signature using his or her private key, and anyone having the signer's public key can verify the signatures. Thus, the verification can be performed without the signer's consent or involvement. In some cases, a signer may not like it that anyone can verify his or her signatures. Thus, in order to increase the privacy of the signer, another scheme called undeniable digital signature scheme was proposed by David Chaum and Hans van Antwerpen in 1989. This scheme is a non-self-authenticating signature scheme in which no signatures can be verified without the signer's cooperation and notification.
This scheme has three components, namely, signing algorithm, verification protocol and disavowal protocol.
 Signing algorithm: This allows the signer (say,
Signing algorithm: This allows the signer (say, A) to sign a message.
 Verification (or confirmation) protocol: This allows the signer to limit the users who can verify his or her signature. The verification process is interactive in nature and uses the challenge/response mechanism for verifying the signature, in which the verifier
Verification (or confirmation) protocol: This allows the signer to limit the users who can verify his or her signature. The verification process is interactive in nature and uses the challenge/response mechanism for verifying the signature, in which the verifier B sends a question (or challenge) to the signer A. A then sends a valid answer (response) to B, and B views the response to verify the signature.
 Disavowal (or denial) protocol: Since the verification process requires the involvement of the signer, it is quite possible that the signer can freely decline the request of the verifier. This protocol prevents the signer from proving that a signature invalid when it is valid, and vice versa. To prove that the signature is a fake,
Disavowal (or denial) protocol: Since the verification process requires the involvement of the signer, it is quite possible that the signer can freely decline the request of the verifier. This protocol prevents the signer from proving that a signature invalid when it is valid, and vice versa. To prove that the signature is a fake, A needs to take part in the denial protocol.
The main advantage of this scheme is that if a signature is invalid, a fraud signer cannot prove it valid because he or she will not be able to successfully complete the verification protocol. In the same way, a fraud signer cannot deny a signature that is valid, as he or she will not be able to successfully complete the disavowal protocol.
14. Explain the mutual authentication protocol.
Ans.: The mutual authentication protocol enables the communicating parties to mutually satisfy themselves about their identities and exchange session keys between them. The main issues with authenticated key exchange are confidentiality and timeliness. Confidentiality can be achieved by communicating the essential identification and session key information in an encrypted form so that the compromise of session keys can be prevented. Timeliness is another important issue that must be considered for preventing message replay attacks. The authenticated key exchange can be managed either using the symmetric-key encryption technique or the public-key encryption technique.
Symmetric-key encryption technique
In this technique, a trusted key distribution centre (KDC) is involved who is responsible for generating a session key that is to be used for a short duration between the two communicating parties for a particular session, as well as for distributing that key to both the parties. Each party shares a master key with the KDC, and the KDC uses the master key for distributing the session key to ensure secure distribution of session keys.
Several protocols were proposed for secret key distribution using a KDC; however, each of them had some weaknesses. Finally, in the early 1990s, a protocol was presented for secure key distribution including authentication. The steps of this protocol are as follows:
 To initiate the authentication exchange,
To initiate the authentication exchange, A generates a nonce NA and sends it to B along with its identifier IDA in plaintext. This nonce will be returned to A later in an encrypted message that includes the session key generated by KDC, to assure A of its timeliness.

B sends a message to KDC that includes its identifier IDB and a nonce NB to request KDC for a session key. B's message also includes a block that instructs KDC to issue credentials to A. This block is encrypted with the secret (or master) key shared between the KDC and B, and includes A's identifier (IDA), A's nonce (NA) and the suggested expiration time for the credentials (TE).
 KDC sends a message to
KDC sends a message to A that includes the following:
 Nonce received from
Nonce received from B(NB)
 A block containing
A block containing B's identifier (IDB) to assure A that the second party is B itself, A's nonce (NA) to assure A that this is a timely message and not a replay, a session key (KS) generated by KDC, and the time of expiration of the key (TE). This block is encrypted with the secret key shared between A and KDC, which is KA.
 A block containing
A block containing A's identifier (IDA), the session key (KS), and the time of expiration of the key (TE). This block is encrypted with the secret key shared between B and KDC (that is, KB). It serves as a “ticket” for A for subsequent authentications.
 A transmits the ticket to
A transmits the ticket to B. A also sends B's nonce encrypted with the session key (KS) to assure B that the message has come from A and not from a replay attack. B uses KS to decrypt the nonce.
These steps are summarized as given below:
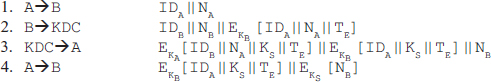
This protocol provides a secure and effective mechanism to establish a session with a secure session key. Suppose A establishes a session with B using this protocol, and then ends that session once the communication is over. Further, assume that within the same time limit TE, A again wants to establish a new session with B. Now, A has the session key KS that can be used for subsequent authentication to B but this time without the involvement of KDC. Thus, A can establish as many sessions he wants within the time limit provided by the protocol using the same session key. Once the time limit is over,
a new session key must be requested from the KDC. The steps for establishing a new session without contacting KDC are as follows:
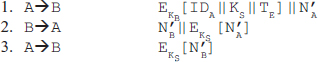
Here, N'A and N'B are newly generated nonces that assure A and B that there is no replay attack. Note that TE is the time relative to B's clock; thus, there is no need to synchronize clocks because B checks only self-generated timestamps.
Public-key encryption technique
In the public-key encryption technique, in addition to generating the session keys, KDC is also responsible for exchanging the public keys of A and B. In this technique, no master key is shared between the KDC and the communicating parties; rather, the public keys of KDC and the communicating parties are used for encryption. The steps of this protocol are as follows:
1. A sends a message to KDC informing that he or she wants to establish a secure connection with B. The message includes the identifiers of A (IDA) and B (IDB) in plaintext.
2. KDC returns a copy of the public-key certificate of B to A, which contains the identifier and public key of B (BPUB), encrypted with the private key of KDC (KDCPRI).
3. A generates a nonce NA and sends it to B along with its identifier (IDA) to inform B that he or she wants to communicate with B. A sends this information by encrypting it with B's public key (BPUB).
4. On receiving this information from A, B sends a request to KDC for issuing the public-key certificate of A, and also for generating a session key (KS). B's request includes the identifiers of A and B in plaintext, along with the nonce NA encrypted with the public key of KDC (KDCPUB).
5. KDC sends a copy of A's public-key certificate (A's identifier plus its public key) to B encrypted with KDCPRI. KDC also sends the session key (KS), nonce NA and B's identifier (IDB). This triplet informs A that KS is bound to NA in order to assure A that KS is a newly generated session key and not an old one. The triplet is first encrypted with KDCPRI to assure B that this information is from KDC itself, and then it is encrypted with B's public key to make sure that no other party can create a fraudulent connection with A.
6. B sends the triplet {NA, KS, IDB} still encrypted with KDC's private key along with the nonce NB to A. This whole information is further encrypted with A's public key (APUB).
7. A decrypts the received information using the public key of KDC (KDCPUB) to obtain the session key (KS). Then, it sends the nonce NB encrypted with the session key KS to B to assure him or her that A has got the session key.
These steps are summarized as given below:
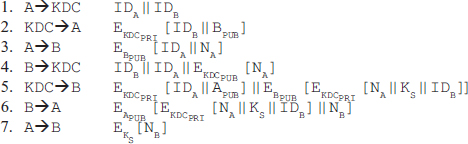
Though this protocol provides protection against several attacks, the authors Woo and Lam themselves found an error and generated a revised version of the algorithm. In the new version of the protocol, the identifier of A (IDA) is added to the information being encrypted with the private key of KDC in steps 5 and 6, as shown here:

The inclusion of IDA binds the session key KS to the identifiers of both A and B that are involved in the communication. IDA is included because of the reason that the nonce NA is considered unique among all the nonces generated by A only, and not among all nonces generated by all parties. Thus, the connection request of A is uniquely identified with the help of a pair {IDA, NA} and not only by NA as in prior protocols.
15. Explain one-way authentication protocol.
Ans.: In some applications, such as e-mail, it is not necessary for the sender and receiver to be online at the same time. The message sent by the sender is rather forwarded to the receiver's electronic mailbox, where it is stored until the receiver reads it. Thus, only one-way authentication is required.
Since the receiver may or may not be online at the time the sender sends an e-mail, a mail-handling mechanism is required that stores the e-mail when the sender sends it, and then forwards it to the receiver at some later time. As we know, an e-mail consists of a header and the message. The header of the e-mail must be clear so that it can be properly handled by the store-and-forward e-mail protocol such as SMTP.
There are two basic requirements for such applications. First, the plaintext form of the e-mail message must not be accessible to the mail-handling protocol. Thus, an e-mail message must be encrypted such that the decryption key is not known to the mail-handling system. Second, the recipient needs to be assured that the message has come from a supposed sender. One-way authentication can also be performed either using symmetric-key encryption technique or public-key encryption technique.
Symmetric-key encryption technique
While using the symmetric-key encryption technique in one-way authentication, the following steps are used.
1. The sender A sends the identifier of A and B, and a nonce N1, to the KDC in plaintext.
2. The KDC then returns a message to A, which contains a newly generated session key KS, B's identifier IDB, the nonce N1, and a block encrypted with the secret key shared between KDC and B (that is, KB). This whole message is further encrypted with the secret key shared between KDC and A (that is, KA). The inclusion of IDB and N1 in the message assures A that this is the original message and that it has not been altered by the KDC in any way. The nonce N1 also helps A in verifying that it is not a replay of some previous message. The block encrypted with KB contains KS and IDA and is intended for B. A will send this block to B as it is to establish the connection and prove A's identity.
3. A forwards to B the message originated from KDC for B, along with the e-mail encrypted with the session key KS.
The protocol is summarized as follows:
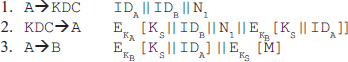
The main advantage of this protocol is that it guarantees that no user other than the intended recipient of the message will be able to read the message. Moreover, it provides a level of authentication that the message has come from an alleged sender. However, this protocol does not provide protection against replay attacks.
Public-key encryption technique
While using the public-key encryption technique for one-way authentication, one can achieve confidentiality, authentication or both. To achieve confidentiality, the sender needs to know the public key of the recipient. If A is the sender and B is the receiver, the following protocol may be used.
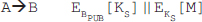
Here, A encrypts the message M with the session key KS, and also encrypts the session key KS with B's public key BPUB, and sends it to B.
To achieve only authentication, B needs to know the public key of A. Thus, the following protocol may be used.
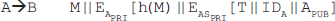
In this protocol, A sends to B the message M, the digital signature encrypted with A's private key, and A's public-key certificate encrypted with the private key of the authentication server (ASPRI). B first determines A's public key from the public-key certificate, and then verifies that it is authentic. B then uses the public key to verify the message itself.
To achieve both confidentiality and authentication, the message M can be encrypted with the session key KS, which is also sent to B encrypting it with B's public key.
16. In the RSA scheme, let p = 3, q = 11 and d = 3. Calculate the public key. Now suppose A wants to send a message M = 107 to B. Sign and verify this message using the RSA digital signature scheme.
Ans.: Here, p = 3 and q = 11
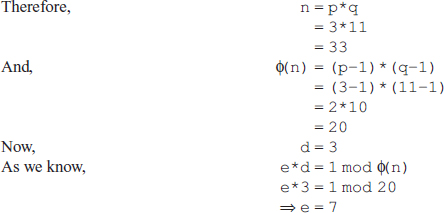
Therefore, the public key is (e, n), that is, (7, 33).
Signing:

Verifying:

Now, we have to verify whether M' ≡ M (mod n)
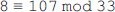
8 ≡ 8, which is true.
Thus, the signature is verified.
17. In the ElGamal scheme, let p = 881, e1 = 2 and d = 127. Calculate the value of e2. Find the values of S1, S2, V1 and V2, if M = 400 and k = 17.
Ans.: Here, p = 881, e1 = 2 and d = 127

Signing:

The multiplicative inverse of 17 in Z880 is 673 (as 17*673 = 11441 mod 880 = 1). The multiplicative inverse can be obtained using the extended Euclidean algorithm discussed in Chapter 2 (Q12).
Therefore, Equation (1) can be written as follows:
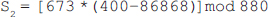
Since 86868 is not lying in Z880, we need to take 86868 mod 880, which is 628. Thus, now the equation becomes:
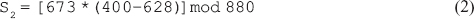
Since 400−628 comes out to be negative, we first take the additive inverse of 628, which can be computed as 880−628 = 252, and then add it to 400. Now, Equation (2) becomes

Therefore, the digital signature = (S1, S2) = (684, 556)
Verifying: Since 0 < 684 < 881 and 0 < 556 < 880, we compute the two verification codes V1 and V2 as follows:

Since V1 ≡ V2, the digital signature is verified.
18. In the DSS scheme, let q = 83, p = 997, e0 = 3 and d = 23. Calculate the values of e1 and e2. Find the values of S1, S2, V1 and V2, if h(M)= 5000 and k = 31.
Ans.: Here, q = 83, p = 997, e0 = 3 and d = 23
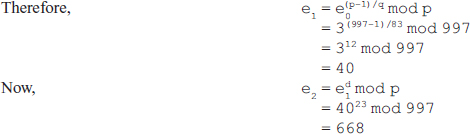
Signing:

The multiplicative inverse of 31 in Z83 is 75 (as 31*75 = 2325 mod 83 = 1).
Therefore, Equation (1) can be written as follows:

Therefore, the digital signature = (S1, S2) = (16, 50)
Verifying: Since 0 < 16 < 83 and 0 < 50 < 83, we compute the verification code Vc as follows:
We first calculate the values of intermediate variables w, z and y.
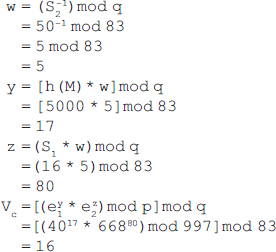
Since S1 ≡ Vc, the digital signature is verified.
Multiple-choice Questions
1. Which of the following services is not provided by digital signatures directly?
(a) Message authenticity
(b) Message confidentiality
(c) Message integrity
(d) Nonrepudiation
2. Which of the following pair of keys is used to create and verify the digital signature, respectively?
(a) Signer's private key and verifier's public key
(b) Verifier's public key and verifier's private key
(c) Signer's private key and signer's public key
(d) Signer's public key and signer's private key
3. The sender encrypts the message with his or her private key to achieve _________.
(a) Authentication
(b) Confidentiality
(c) Both (a) and (b)
(d) None of these
4. RSA _________ be used for digital signatures.
(a) can
(b) cannot
(c) must
(d) must not
5. Which of the following is a property of a digital signature?
(a) It must be able to verify the author.
(b) It must be able to verify the date and time of the signature.
(c) It must be able to authenticate the contents of the message at the time of the signature.
(d) All of these
6. Which of these is a kind of attack possible on digital signatures?
(a) Ciphertext-only attack
(b) Known-message attack
(c) Key-only attack
(d) Both (b) and (c)
7. Which of these statements is not correct about DSS?
(a) It was published by the National Institute of Standards and Technology.
(b) It uses three functions to create a digital signature.
(c) An elaborated version of DSS was named as FIPS 186-2.
(d) It uses Secure Hash Algorithm (SHA).
8. Which of these is not a variation of a digital signature?
(a) Timestamped signature
(b) Blind signature
(c) Encrypted digital signature
(d) Undeniable digital signature
Answers
1. (b)
2. (c)
3. (a)
4. (a)
5. (d)
6. (d)
7. (b)
8. (c)
1. Explain the working principle of the Kerberos protocol.
Ans.: Kerberos is an authentication protocol that has been designed to be used in an open distributed environment, where the users at workstations request for the services on the servers distributed throughout the network. It basically provides a centralized authentication server that is responsible for authenticating users to servers and servers to users. Its name has been derived from Greek mythology after the name of a three-headed dog that guarded the gates of Hades. Kerberos has become very popular as it can also act as a KDC in addition to being an authentication protocol. It was originally developed as a part of Project Athena at the MIT. Several versions of Kerberos have evolved. However, the most commonly used version of Kerberos is version 4. The Kerberos protocol has four components, namely, client workstation, authentication server (AS), ticket-granting server (TGS) and real server.
 Client workstation is an entity that wants to access services from a server.
Client workstation is an entity that wants to access services from a server.
 Authentication server (AS) acts as a KDC in the Kerberos protocol. It is responsible for the verification of the identity of users during login. To get verified, the users first need to register themselves with the AS. Each registered user is assigned a unique ID and a password. All the IDs and their corresponding passwords are stored in a centralized database of AS. In addition to verifying the users, it also issues a session key to the requesting user, which is to be used between the user and the TGS, and sends a ticket for the TGS. AS also shares a unique secret key with each server, and hence, all the servers also need to register themselves with AS.
Authentication server (AS) acts as a KDC in the Kerberos protocol. It is responsible for the verification of the identity of users during login. To get verified, the users first need to register themselves with the AS. Each registered user is assigned a unique ID and a password. All the IDs and their corresponding passwords are stored in a centralized database of AS. In addition to verifying the users, it also issues a session key to the requesting user, which is to be used between the user and the TGS, and sends a ticket for the TGS. AS also shares a unique secret key with each server, and hence, all the servers also need to register themselves with AS.
 Ticket-granting server (TGS) is responsible for issuing tickets for establishing connection with the real server. It also issues the session key, which is to be used between the user and the real server. Once a user has got verified by AS, he or she can contact TGS any number of times to obtain the tickets for different real servers.
Ticket-granting server (TGS) is responsible for issuing tickets for establishing connection with the real server. It also issues the session key, which is to be used between the user and the real server. Once a user has got verified by AS, he or she can contact TGS any number of times to obtain the tickets for different real servers.
 Real server provides the required services to the user. Here, the user uses its own process (client process) to access the server process using a client-server program (e.g. FTP).
Real server provides the required services to the user. Here, the user uses its own process (client process) to access the server process using a client-server program (e.g. FTP).
The working of Kerberos is shown in Figure 9.1. To understand how the Kerberos protocol operates, consider a user A who wants to access the services of a real server B. The user A can access the processes running on B by performing the following steps.
1. The user A logs in to the workstation by entering his or her user ID (say, IDA). The workstation then sends IDA in plaintext to AS.

Figure 9.1 Kerberos Protocol
2. In response, the AS creates a message that includes two items: a randomly generated session key KA−TGS and the ticket for TGS, which is encrypted with the secret key shared between the AS and TGS (KAS−TGS). This whole message is encrypted with the symmetric key of A (KA). The session key KA−TGS is used by the user to contact the TGS. Now, this encrypted message is sent to A.
3. On receiving the message, A's workstation asks him or her for the password. When A enters the correct password, the workstation generates the symmetric key (KA) by applying an appropriate algorithm (generally a hash function) on the password. The password is then immediately destroyed, so that it cannot be stolen by anyone. The symmetric key KA is now used to decrypt the received message. Once the message is decrypted, the ticket for TGS and the session key KA−TGS are extracted. Since the ticket is encrypted with the symmetric key of TGS, only TGS can open it. A now sends a message to TGS containing the ticket received from AS, the name of the real server (B) and a timestamp T encrypted with the session key KA−TGS. This timestamp prevents replay attacks from any other user.
4. The TGS now sends two tickets each for A and B. Both these tickets contain the session key (KA−B) to be used between A and B. A's ticket is encrypted with the secret key (KA−TGS) shared between A and TGS, while the ticket for B is encrypted with the secret key (KTGS−B) shared between TGS and B. This mechanism provides security for the whole process. No other user can extract KA−B, as he or she does not know KA−TGS or KTGS−B. Moreover, step 3 cannot be replayed, since an unauthorized user cannot replace the timestamp with a new one (as he or she does not know KA−TGS).
5. A now sends B's ticket with a timestamp encrypted with KA−B.
6. B acknowledges the receipt of the ticket by adding 1 to the timestamp. It also encrypts the message with KAB and sends it to A.
Now, suppose A wishes to receive services from different servers, then it only has to repeat steps 3 to 6. The first two steps involve the verification of A's identity, which remains same for all the servers. Thus, steps 1 and 2 need not be repeated.
2. Discuss the basic requirements for Kerberos.
Ans.: There are four basic requirements that have been defined for Kerberos. These requirements are as follows:
 Security: Kerberos should be secure enough to prevent eavesdroppers from obtaining any kind of information that is necessary to impersonate a user.
Security: Kerberos should be secure enough to prevent eavesdroppers from obtaining any kind of information that is necessary to impersonate a user.
 Reliability: Kerberos should be highly reliable and should support distributed server architecture so that, in case of failure of one system, some other system can act as a backup.
Reliability: Kerberos should be highly reliable and should support distributed server architecture so that, in case of failure of one system, some other system can act as a backup.
 Transparency: Kerberos should be transparent, such that the user is not able to know that authentication is taking place; the user should only be required to enter his or her password.
Transparency: Kerberos should be transparent, such that the user is not able to know that authentication is taking place; the user should only be required to enter his or her password.
 Scalability: Kerberos should support a modular, distributed architecture, so that it can support a large number of clients and servers.
Scalability: Kerberos should support a modular, distributed architecture, so that it can support a large number of clients and servers.
3. Define the terms ‘Kerberos realm’ and ‘Kerberos principal’.
Ans.: A typical Kerberos environment consists of an authentication server (or a Kerberos server), a number of clients all registered with the authentication server and a number of application servers that provide several services. The Kerberos server must maintain a centralized database that contains the user IDs and hashed passwords of all the users registered with the Kerberos server. It must also share a unique secret key with each application server. All servers need to get registered with the Kerberos server. Such an environment is called Kerberos realm. It is basically a single administrative domain.
The computer system where the Kerberos database is stored (referred to as Kerberos master computer system) should be kept in a physically secure room. The person having the Kerberos master password is only authorized to modify the contents of the Kerberos database. Though several read-only copies of this database can be kept on other Kerberos computer systems, changes can only be made on the master computer system. If there exist several Kerberos realms, then they must share secret keys and trust among themselves.
Kerberos principal is a unique identity to which Kerberos can assign tickets. In other words, all the services or the users known to a Kerberos system are referred to as Kerberos principals. Each Kerberos principal is identified by its principal name. A Kerberos principal has the following form:
primary[/instance]@REALM
Principal is divided into three parts: the primary (service or user name), the instance, and the realm.
 Primary: This is the first part of the principal. For a user, the primary is the
Primary: This is the first part of the principal. For a user, the primary is the username and, for a host, the primary is the word host.
 Instance: This is an optional string that qualifies the primary, and is separated from the primary by a slash (/). In case of a user, the instance is generally
Instance: This is an optional string that qualifies the primary, and is separated from the primary by a slash (/). In case of a user, the instance is generally NULL; however, in some cases, it can have some value (e.g. admin).
 Realm: This is the last component of the principal, and is basically the Kerberos realm. It is generally separated from the rest of the principal by the ‘@’ symbol. In most cases, it is your domain name and must be specified in upper-case letters.
Realm: This is the last component of the principal, and is basically the Kerberos realm. It is generally separated from the rest of the principal by the ‘@’ symbol. In most cases, it is your domain name and must be specified in upper-case letters.
For example, consider the following principals:
robert@ATHENA.MIT.EDU robert/admin@ATHENA.MIT.EDU
In the first principal, robert is primary, instance is NULL and ATHENA.MIT.EDU is realm. In the second principal, robert is primary, admin is instance and ATHENA.MIT.EDU is realm.
4. Discuss the steps involved in inter-realm communication in Kerberos.
Ans.: In a system that crosses organizational boundaries, it is not feasible for all users to be registered with a single AS; rather, multiple ASs will exist with each AS responsible for the registration and authentication of the users and servers within a single realm. In case two users (say, A and B) of
different realms want to communicate with each other, they need to obtain service tickets to access resources in foreign realms. In order to access such services, these steps are followed:
1. The user A contacts the AS of their realm asking for a ticket that will be used with the TGS of the foreign realm. If both the realms share keys and have established a trusted relationship between them, the corresponding AS of A's realm delivers the requested ticket to A.
2. In case A's realm does not share keys with the foreign realm, the AS of A's realm will provide a ticket for an intermediary foreign realm that may be sharing the keys with the target realm.
3. The client can use this ‘intermediary ticket’ to communicate with the AS of the intermediary foreign realm, which will either follow step 2, or it will issue a ticket that can be used with the AS of the target realm (in case it shares keys with the target realm).
4. The client uses this ticket to obtain the service ticket from the TGS of the foreign realm.
5. The user can now use this service ticket to obtain the services of the desired server.
5. How is the encryption key generated from the password in Kerberos?
Ans.: In Kerberos, the user can enter a password of any length; however, the password is restricted to contain only those characters that can be represented in a 7-bit ASCII format. This password is used to generate the symmetric key of the user that is to be used for decrypting the messages received from AS. The steps involved in password-to-key transformation are as follows:
1. The user enters his or her password in the form of a character string (say, s).
2. The character string s is converted into a bit string (say, b) in such a way that the first character of s is stored in the first seven bits of b, the second character is stored in next seven bits and so on, as shown in Figure 9.2(a). That is:
b[0]represents bit 0 ofs[0]…b[6]represents bit 6 ofs[0]b[7]represents bit 0 ofs[1]…b[13]represents bit 6 ofs[1]…b[7i+j]represents bitjofs[i]where, 0 <=j<= 6
3. The bits in the bit string b are aligned in a ‘fanfold’ manner, such that the bits 0 to 55 form the first row, then the bit 56 is placed below the bit 55, bit 57 is placed below 54, bit 58 is placed below 53 and so on, as shown in Figure 9.2(b).
4. A bitwise XOR operation is performed to compact the bit string to 56 bits. For example, if the bit string is of length 60, then
b[55] = b[55]  b[56]
b[56]
b[54] = b[54]  b[57]
b[57]
b[53] = b[53]  b[58]
b[58]
b[52] = b[52]  b[59]
b[59]
This creates a 56-bit DES key [see Figure 9.2(b)]. Note that steps 3 and 4 are performed to compact the bit string.
5. The 56-bit string is then expanded to a 64-bit input key K. For this, the 56-bit key is divided into 7-bit blocks (total 8 blocks), and then each 7-bit block is mapped to a corresponding block of 8 bits, thus creating a 64-bit key.

Figure 9.2 Password-to-key transformation in Kerberos
6. The password supplied by the user is encrypted with the key K using the cipher block chaining (CBC) mode of DES [see Figure 9.2(c)]. This process results in a 64-bit block, referred to as CBC checksum, which becomes the encryption key (say, Kpw) associated with the user's password.
6. Explain the differences between Kerberos version 4 and Kerberos version 5.
Ans.: Though Kerberos version 4 is most commonly used, it suffers from some environmental shortcomings and technical deficiencies. Kerberos version 5 attempts to overcome these problems. The differences between Kerberos versions 4 and 5 based on the environmental shortcomings are listed in Table 9.1.
| Issue | Kerberos 4 | Kerberos 5 |
|---|---|---|
| Encryption system dependence | Requires the use of DES algorithm. | Any encryption algorithm can be used. To make this possible, an encryption type identifier is attached with the ciphertext. |
| Internet protocol dependence | Uses only IP addresses, and no other address can be used in it. | Allows the use of any network address, such as the ISO network address. This is possible due to the reason that the network addresses are labelled with type and length. |
| Message byte ordering | The byte ordering in the message is not uniform. The sender can include either the least significant byte or the most significant byte in the lowest address. That is, the sender has the freedom of choosing his or her own byte ordering. | The byte ordering in the message is uniform. All the message structures are defined using two standards, namely, Abstract Syntax Notation One (ASN.1) and Basic Encoding Rules (BER), thereby providing unambiguous byte ordering. |
| Ticket lifetime | The lifetime of the ticket is limited. The lifetime values are encoded in 8-bit quantities, in units of 5 minutes. Thus, the maximum possible lifetime is 28 * 5 = 1280 minutes or 21 hours, approximately. This time limit may not be sufficient for some applications, such as a long-running simulation. | The tickets can have arbitrary lifetime values. To allow this, an explicit start and end time is included with each ticket. |
| Authentication forwarding | The credentials issued to one client cannot be forwarded to some other host or some other client. | The credentials issued to one client can be forwarded to another. This would allow a client to access a server, and that server to access another server on behalf of the client's credentials. This technique is termed as transitive cross-realm authentication. For example, a print server can access the file server to retrieve the file to be printed on behalf of the client. |
| Inter-realm authentication | The number of Kerberos-to-Kerberos relationships required for interoperability among N realms is calculated as N2 , where N is the number of realms. |
A lesser number of relationships are required. |
In addition to the environmental shortcomings mentioned in the preceding text, version 4 suffers from some technical deficiencies. Version 5 is intended to address these deficiencies. These deficiencies are listed in Table 9.2.
| Issue | Kerberos 4 | Kerberos 5 |
|---|---|---|
| PCBC encryption | Uses a nonstandard mode of the DES algorithm known as propagating cipher block chaining (PCBC) for encryption. The PCBC was supposed to provide an integrity check as part of the encryption operation; however it is found to be prone to an attack that involves the interchange of ciphertext blocks. | Uses the standard cipher block chaining (CBC) mode for encryption. It provides explicit integrity mechanisms such as attaching hash code or checksum to the message before encryption using CBC. |
| Session keys | The session key included in each ticket serves two purposes. First, it is used by the client to encrypt the authenticator sent to the server associated with that ticket. Second, it can be used to encrypt the messages between a client and a server. Since the same ticket is used more than once for accessing a particular server, it leads to the possibility of a replay attack by a third party. | Allows a client and a server to negotiate a sub-session key, which is to be used only for the current session. Thus, if the client wishes to access the server again, he or she would require a new sub-session key. |
| Password attacks | Does not provide a secured mechanism for preventing password attacks. Whenever AS sends a message to the client, it is encrypted with the key based on the client's password. This message can be captured by an opponent who may then attempt to decrypt it by trying various passwords. If the opponent chooses the right mechanism to acquire the password, then he or she can use it to acquire the authentication credentials from Kerberos. | Though version 5 does not completely prevent the password attacks, it provides a preauthentication mechanism that makes the password attacks more difficult. |
7. Define the terms forwardable, renewable and postdatable tickets.
Ans.: Kerberos version 5 supports the use of forwardable, renewable and postdatable tickets.
 Forwardable ticket: This ticket can be used by the user to get a new ticket on behalf of the current credentials. This allows the user to get validated on other machines also. However, the user has to use a different IP address.
Forwardable ticket: This ticket can be used by the user to get a new ticket on behalf of the current credentials. This allows the user to get validated on other machines also. However, the user has to use a different IP address.
 Renewable ticket: As the name suggests, this ticket can be renewed by asking the KDC to issue a new ticket with an extended lifetime. Note that a ticket can only be renewed before the expiration of its time limit. It is similar to renewing an insurance policy or a credit card before the validity is expired.
Renewable ticket: As the name suggests, this ticket can be renewed by asking the KDC to issue a new ticket with an extended lifetime. Note that a ticket can only be renewed before the expiration of its time limit. It is similar to renewing an insurance policy or a credit card before the validity is expired.
 Postdatable ticket: This ticket is similar to a postdated cheque, which bears a starting time as some time in the future. Thus, the ticket is initially invalid. A postdatable ticket can only be used after getting it validated from the KDC during its valid lifetime.
Postdatable ticket: This ticket is similar to a postdated cheque, which bears a starting time as some time in the future. Thus, the ticket is initially invalid. A postdatable ticket can only be used after getting it validated from the KDC during its valid lifetime.
8. Explain the X.509 authentication service and its certificates.
Ans.: X.509 was designed by ITU-T to describe the public-key certificates in a structured way. It is a part of the X.500 series of recommendations that define a directory service. A directory is basically a server or a set of servers distributed over a network that maintains a database of information about the users, such as mappings from user names to network addresses. X.509 provides authentication services to its users through the X.500 directory, which may act as the repository of public-key certificates associated with each user. Each certificate contains the public key of the user and is signed by the private key of the trusted certification authority (CA). It may be noted that only the CA can create the user certificates and place them in the directory. The directory server itself is not responsible for creating public keys or certificates; it simply acts as a warehouse of certificates for the users.
X.509 also defines a set of alternative authentication protocols based on the use of public-key certificates. The format of the certificate and the authentication protocols defined in X.509 are used in several contexts such as IP Security, S/MIME, SSL/TLS and SET, and hence it is considered to be an important standard.
The first version of X.509 was issued in 1988. Then, in 1993, its second version came out, to address some of the security concerns. A third version was released in 1995, which was revised in 2000. X.509 makes uses of the ASN.1 (Abstract Syntax Notation One) protocol, which defines the general format of the X.509 certificate with several fields, as shown in Figure 9.3. The description of these fields is as follows:
 Version number: This field differentiates among the various versions of the certificate format. That is, the version of X.509 is specified in this field. The first version number was 0, and the current version (third version) is 2.
Version number: This field differentiates among the various versions of the certificate format. That is, the version of X.509 is specified in this field. The first version number was 0, and the current version (third version) is 2.

Figure 9.3 X.509 Certificate Format
 Serial number: This field contains an integer value assigned to each certificate. This value is unique within the issuing CA.
Serial number: This field contains an integer value assigned to each certificate. This value is unique within the issuing CA.
 Signature algorithm ID: This field specifies the algorithm used by CA to sign the certificate, together with any associated parameters.
Signature algorithm ID: This field specifies the algorithm used by CA to sign the certificate, together with any associated parameters.
 Issuer name: This field specifies the name of the CA that has created and signed the certificate. The name is usually specified as a hierarchy of strings that include the name of the country, state, organization, department and so on.
Issuer name: This field specifies the name of the CA that has created and signed the certificate. The name is usually specified as a hierarchy of strings that include the name of the country, state, organization, department and so on.
 Validity period: This field specifies the lifetime of the certificate. It includes the earliest time and latest time; the certificate is invalid before the earliest time and after the latest time.
Validity period: This field specifies the lifetime of the certificate. It includes the earliest time and latest time; the certificate is invalid before the earliest time and after the latest time.
 Subject name: This field specifies the entity to which this certificate refers. That is, this certificate certifies the public key of the user who is holding the corresponding private key. This field is also specified as a hierarchy of strings; one of the strings is called the common name, which is the actual name of the user.
Subject name: This field specifies the entity to which this certificate refers. That is, this certificate certifies the public key of the user who is holding the corresponding private key. This field is also specified as a hierarchy of strings; one of the strings is called the common name, which is the actual name of the user.
 Subject public key: This field specifies the main content of the certificate, which is the public key. It also specifies the corresponding public-key algorithm and its associated parameters.
Subject public key: This field specifies the main content of the certificate, which is the public key. It also specifies the corresponding public-key algorithm and its associated parameters.
 Issuer unique identifier: This is an optional field that specifies the unique identifier of the authority issuing the certificate. This field allows having the same value in the issuer name field of two different certificates, provided they have different values in the issuer unique identifier field.
Issuer unique identifier: This is an optional field that specifies the unique identifier of the authority issuing the certificate. This field allows having the same value in the issuer name field of two different certificates, provided they have different values in the issuer unique identifier field.
 Subject unique identifier: This is also an optional field, which specifies the unique identifier of the subject to which the certificate is issued. This field allows having the same value in the subject name field of two different certificates, provided they have different values in the subject unique identifier field.
Subject unique identifier: This is also an optional field, which specifies the unique identifier of the subject to which the certificate is issued. This field allows having the same value in the subject name field of two different certificates, provided they have different values in the subject unique identifier field.
 Extensions: This field is used by the issuers to add more private information to the certificate. The extensions were added in the third version of X.509. This is also an optional field.
Extensions: This field is used by the issuers to add more private information to the certificate. The extensions were added in the third version of X.509. This is also an optional field.
 Signature: This field is divided into three sections as discussed in the following:
Signature: This field is divided into three sections as discussed in the following:
 The first section includes all the other fields in the certificate.
The first section includes all the other fields in the certificate.
 The second section contains the digest of the first section, which is encrypted with the private key of CA.
The second section contains the digest of the first section, which is encrypted with the private key of CA.
 The third section includes the algorithm identifier that has been used to create the second section.
The third section includes the algorithm identifier that has been used to create the second section.
9. Explain the terms certificate renewable and certificate revocation with respect to X.509. Also, discuss how the format of the X.509 certificate is different from that of the certificate revocation list?
Ans.: The X.509 certificates have a validity associated with them. If everything goes smoothly, then the certificates can be renewed by the CA. A new certificate is issued before the validity of the old one expires. This process is known as certificate renewal. However, sometimes, the certificate has to be revoked before the validity of the certificate expires. This is known as certificate revocation. The certificates can be revoked due to several reasons. Some of them are as follows:
 The private key of the user might have been compromised.
The private key of the user might have been compromised.
 The private key of the CA that can verify the certificates might have been compromised. In this case, the CA must revoke all unexpired certificates.
The private key of the CA that can verify the certificates might have been compromised. In this case, the CA must revoke all unexpired certificates.
 The certificate authority is no longer willing to issue a certificate to the user.
The certificate authority is no longer willing to issue a certificate to the user.
The certificate revocation is implemented by periodically issuing a Certificate Revocation List (CRL), which contains all the revoked certificates that have not expired till the issue date of the CRL. A typical format of CRL is shown in Figure 9.4. It contains many fields, some of which are the same as in the X.509 certificate. The fields common to both X.509 certificates and CRL are signature algorithm ID, issuer name and signature. The fields that are new in CRL are as follows:

Figure 9.4 Certificate Revocation List Format
 This update date: This field defines the issue date of CRL.
This update date: This field defines the issue date of CRL.
 Next update date: This field specifies the date when the list will be issued next.
Next update date: This field specifies the date when the list will be issued next.
 Revoked certificate: This is a repeated list of all the certificates that are not expired and have been revoked. Each list is divided into two sections, namely, user certificate serial number and revocation date.
Revoked certificate: This is a repeated list of all the certificates that are not expired and have been revoked. Each list is divided into two sections, namely, user certificate serial number and revocation date.
10. What do you understand by directory authentication service?
Ans.: The directory authentication service is used when two entities wish to communicate with each other, and each of them needs to authenticate the other. That is, both the sender and receiver need to ensure that the other communicating party is the one that it claims to be. There are two types of directory authentication services, namely, peer entity authentication and data origin authentication.
 Peer entity authentication: This authentication service enables the user to verify the identity of a peer entity involved in the communication process. It prevents an entity from masquerading as another entity or an unauthorized replay of a previously established connection. The peer entity service can be used during the establishment phase or occasionally during the data transfer phase of a connection. Note that there must be an association between the two parties for peer entity authentication.
Peer entity authentication: This authentication service enables the user to verify the identity of a peer entity involved in the communication process. It prevents an entity from masquerading as another entity or an unauthorized replay of a previously established connection. The peer entity service can be used during the establishment phase or occasionally during the data transfer phase of a connection. Note that there must be an association between the two parties for peer entity authentication.
 Data origin authentication: This authentication service enables the recipient to verify that the message has not been tampered with in transit (data integrity) and that it has originated from the expected sender (authenticity). That is, it is used to verify the original source of a received message. The data origin authentication services allow the receiver to verify the identity of the message as belonging to the original message creator even if the message has passed through one or more intermediaries before arriving at the receiver. Note that unlike peer entity authentication, no association between the sender and receiver is required. Thus, this type of service is suitable for e-mail service in which there is initially no communication between the entities.
Data origin authentication: This authentication service enables the recipient to verify that the message has not been tampered with in transit (data integrity) and that it has originated from the expected sender (authenticity). That is, it is used to verify the original source of a received message. The data origin authentication services allow the receiver to verify the identity of the message as belonging to the original message creator even if the message has passed through one or more intermediaries before arriving at the receiver. Note that unlike peer entity authentication, no association between the sender and receiver is required. Thus, this type of service is suitable for e-mail service in which there is initially no communication between the entities.
11. Discuss the authentication procedures of X.509.
Ans.: X.509 includes three authentication procedures, namely, one-way authentication, two-way authentication and three-way authentication. These authentication procedures make use of public-key signatures and can be used across a variety of applications. While working with these procedures, it is assumed that two communicating nodes know each other's public key. These procedures are discussed in the following.
 One-way authentication: This involves a single transfer of information from user
One-way authentication: This involves a single transfer of information from user A to user B [see Figure 9.5(a)]. This information is transferred in order to confirm that the message is generated by user A, and that the message is intended for user B and has not been altered or replayed by any intruder. Thus, this procedure only verifies the identity of A. At a minimum, the message includes the following and is signed with the private key of A.
 Timestamp (
Timestamp (tA): This indicates the time when the message was generated, along with the validity or expiration time of the message.
 Nonce (
Nonce (rA): This is a random number used to protect the message from replay attacks. The value of nonce must be unique during the validation period. This is done so that B can discard any new messages having the same nonce value.
 Identity of
Identity of B (IDB): This is included so that the user B can access the X.509 directory and be sure that the message is intended for him or her only.
 Signed data (
Signed data (sgnData): This is the information that is actually conveyed between the two users. This information is included within the scope of the signature, thus ensuring its authenticity and integrity.
 Encrypted data (
Encrypted data (EBPUB[KAB]): This includes the session key KAB, encrypted with B's public key (BPUB). This key is used after the authentication process gets over.
 Two-way authentication: This involves a two-way transfer of information; first from user
Two-way authentication: This involves a two-way transfer of information; first from user A to B, and then from user B to A. This two-way transfer allows both users to verify each other's identity. First, A sends a message containing the same fields as described in one-way authentication to B. Then, B replies to A with a message including tB, rB, IDA, rA, sgnData and optionally EAPUB[KAB], and the message is signed by B [see Figure 9.5(b)]. The inclusion of nonce rA in the reply message ensures that the reply is valid and has come from B, whereas rB protects the information being transferred by B from replay attacks.

Figure 9.5 Authentication Procedures
 Three-way authentication: This involves the three-way transfer of information from
Three-way authentication: This involves the three-way transfer of information from A to B. In this procedure, a third message from A to B is included, in addition to two messages that are the same as described in two-way authentication. The third message contains a signed copy of the nonce rB signed by A [see Figure 9.5(c)]. Since both the nonces are echoed back by the other side, each user can check the returned nonce to detect replay attacks. This approach is useful when synchronized clocks are not available.
12. Explain the services of PGP.
Ans.: PGP (stands for pretty good privacy) is a simple protocol that was invented by Phil Zimmermann to provide confidentiality, authentication and integrity services for electronic mail and other file storage applications. PGP offers various services, which are discussed as follows:
Authentication only
PGP provides digital signature service for authentication. Suppose user A wants to send a message to B, then, to achieve authentication, these steps are followed.
1. A creates a message, and applies the SHA-1 algorithm to find the 160-bit hash code of the message.
2. The generated hash code is encrypted with RSA using A's private key. The resultant encrypted code is then added to the beginning of the message.
3. On receiving the message, B decrypts the message with RSA using A's public key and extracts the hash code.
4. A new hash code for the message is also generated at B's end, and it is compared with the decrypted hash code. If both are same, the message is accepted as authentic; otherwise it is rejected.
Due to the use of both SHA-1 and RSA, the digital signature scheme becomes effective. The use of RSA assures the receiver that the signature can only be generated by the owner of the private key, whereas SHA-1 ensures that no intruder can create a new message with the same hash code, and hence, the signature of the original message. Alternatively, signatures can also be generated using DSS/SHA-1.
Confidentiality only
The confidentiality service is provided by encrypting the messages that are to be transmitted, or to be stored on the local server. The three commonly used symmetric encryption algorithms are CAST-128, IDEA and 3DES. Note that, in PGP, each session key is used only once, and hence, a new key needs to be generated each time a message is to be transmitted. The key is generated as a random 128-bit number, bound to the message and transmitted with it. To provide protection for the key, it is encrypted with the receiver's public key. The steps to achieve confidentiality are as follows.
1. A creates a message and a random 128-bit number. This number is used as a session key K for this message.
2. A encrypts the message using the CAST-128 (or IDEA or 3DES) encryption algorithm with the session key K.
3. The session key K is encrypted with B's public key using RSA (or ElGamal). The encrypted key is then added to the beginning of the message.
4. On receiving the message, B uses its private key to decrypt and recover the session key K.
5. The message is finally decrypted using the session key K.
Confidentiality and Authentication
In some cases, both the confidentiality and authentication services are required for the same message. In such situations, the following sequence is used:
1. The sender A first signs the plaintext message using his or her private key. The signature is then added to the beginning of the message.
2. The signature and the plaintext message together are encrypted with the session key using CAST-128, IDEA or the 3DES algorithm.
3. The session key is encrypted with B's public key using the RSA or ElGamal algorithm.
4. On receiving the message, B uses its private key to decrypt and recover the session key K.
5. B then decrypts with session key K to recover the plaintext message and signature.
6. To verify the signature, a new hash code for the message is computed at B's end and compared with the decrypted hash code. If both are the same, the message is accepted as authentic; otherwise, it is rejected.
Compression
By default, PGP compresses the messages using the ZIP compression algorithm after applying the signature, however, before encrypting them. This saves space for e-mail transmission as well as for file storage. There are two reasons for signing an uncompressed message, which are discussed in the following:
 Generally, the signed messages along with signatures need to be stored for future verification. If an uncompressed message is signed, then the message and the signature can be stored together and retrieved when verification is required. However, if a compressed message is signed, then either the compressed message needs to be stored or the message needs to be recompressed when verification is required.
Generally, the signed messages along with signatures need to be stored for future verification. If an uncompressed message is signed, then the message and the signature can be stored together and retrieved when verification is required. However, if a compressed message is signed, then either the compressed message needs to be stored or the message needs to be recompressed when verification is required.
 Even if the user is ready to recompress the message dynamically for verification, then also PGP's compression algorithm presents certain problems. The main problem is that the algorithm is nondeterministic in nature; that is, the various implementations of the algorithm produce different compressed forms at different times. This is because they achieve different tradeoffs in running speed versus compression ratio. However, all the implementations are interoperable as any version of the algorithm can correctly decompress the output of any other version. If the signature is created after compression, it would restrict all PGP implementations to use the same version of the compression algorithm.
Even if the user is ready to recompress the message dynamically for verification, then also PGP's compression algorithm presents certain problems. The main problem is that the algorithm is nondeterministic in nature; that is, the various implementations of the algorithm produce different compressed forms at different times. This is because they achieve different tradeoffs in running speed versus compression ratio. However, all the implementations are interoperable as any version of the algorithm can correctly decompress the output of any other version. If the signature is created after compression, it would restrict all PGP implementations to use the same version of the compression algorithm.
Encrypting the message after encryption strengthens the cryptographic security. Since, the compressed message contains less redundancy than the plaintext (or uncompressed) message, it would be more difficult to perform cryptanalysis.
E-mail Compatibility
When PGP is used, the encryption has to be done in at least a portion of the message to be transmitted. These encrypted blocks are made of a stream of arbitrary 8-bit octets that are not supported by many e-mail systems as they permit the use of only ASCII text. To make the encrypted blocks compatible with e-mail systems, PGP converts the 8-bit octets into a stream of printable ASCII characters. For this, it uses the radix-64 conversion scheme. In this scheme, each group of three octets is converted into four ASCII characters. A CRC is also added at the end of the block for detecting any transmission errors.
One problem with this conversion scheme is that it expands a message by 33%. Thus, the message needs to be more compressed so that it compensates for the radix-64 expansion. Another main disadvantage of the radix-64 format is that it blindly performs the conversion regardless of the content, even if the input is ASCII text. Thus, when a message containing ASCII text is signed but not encrypted will be converted by radix-64, the output becomes unreadable for the normal user. To overcome this, PGP can be configured to convert only the signature part to radix-64 format, thus making the message readable by normal users without using PGP. The signature would still have to be verified using PGP.
Segmentation and Reassembly
E-mail facilities generally impose a restriction on the maximum length of the message to be transmitted (generally 50,000 octets). Thus, to send a message having length longer than maximum specified, it has to be broken down into smaller parts, and each part needs to be mailed individually. To achieve this, PGP uses segmentation and reassembly functions. If a PGP message is too large, then it is broken down into smaller segments that are of standard e-mail message size. The segmentation is performed after all other processing on the message has been done (even after radix-64 conversion); otherwise, all the processing needs to be done on each segment. Thus, only the first segment contains the session key component and signature component of the message. The segmented message is reassembled at the receiver's end, removing the e-mail headers from each segment. It must be noted that reassembling is performed before applying radix-64 conversion, decryption and decompression.
13. Discuss the steps that are followed for the transmission and reception of PGP messages.
Ans.: The PGP messages are transmitted from the sender to receiver using the following steps:
1. If signature is required, the hash code of the uncompressed plaintext message is created and encrypted using the sender's private key.
2. The plaintext message plus the signature are compressed using the ZIP compression algorithm.
3. The compressed plaintext message plus compressed signature (if present) are encrypted with a randomly generated session key to provide confidentiality. The session key is then encrypted with the recipient's public key and is added to the beginning of the message.
4. The entire block is converted to radix-64 format.
On receiving the PGP message, the receiver follows the reverse process, as described in the following:
1. The entire block is first converted back to binary format.
2. The recipient recovers the session key using his or her private key, and then decrypts the message with the session key.
3. The decrypted message is then decompressed.
4. If the message is signed, the receiver needs to verify the signature. For this, he or she computes a new hash code and compares it with the received hash code. If they match, the message is accepted; otherwise, it is rejected.
14. What are key rings in PGP?
Ans.: When a sender needs to send messages to many people, then he or she requires the key rings. In this case, a sender needs to have two sets of rings—one is a ring of private/public keys, and other is a ring of public keys. The ring of private/public keys includes different key pairs of public and private keys that are owned by the sender, and the ring of public keys includes public key of each user with whom the sender wants to communicate. There are two reasons for keeping various pairs of private/public keys, which are discussed as follows:
 The sender might wish to change his private/public key pair from time to time for more secured communication.
The sender might wish to change his private/public key pair from time to time for more secured communication.
 The sender may want to use different key pairs for different community of people such as friends, colleagues, etc.
The sender may want to use different key pairs for different community of people such as friends, colleagues, etc.
Note that the private/public key ring is stored only on the machine of the user who owns the key pairs, so that it is accessible to that user only.
15. How does PGP use the concept of trust and legitimacy?
Ans.: Like other protocols, PGP also makes use of certificates to authenticate public keys. However, the process is completely different. In PGP, no certification authority (CA) is involved; rather, anyone in the ring can sign a certificate for others in the ring. Thus, PGP certificates are not issued by any certification authority; rather, the users themselves are responsible for issuing certificates to each other. The entire working of PGP is based on the introducer trust, the certificate trust and the key legitimacy.
 Introducer (or producer) trust levels: Since there is no certification authority that the PGP users can trust, the users have to maintain a level of trust among each other. The introducer trust level
indicates the trustworthiness of the introducer (the user who issues certificates to other users). PGP defines three levels of trusts, namely, none, partial, and full. For example, user
Introducer (or producer) trust levels: Since there is no certification authority that the PGP users can trust, the users have to maintain a level of trust among each other. The introducer trust level
indicates the trustworthiness of the introducer (the user who issues certificates to other users). PGP defines three levels of trusts, namely, none, partial, and full. For example, user A can have full trust on user B, partial trust on users C and D and no trust on user E. It must be noted that there is no way in PGP to determine the trustworthiness of the introducer; it entirely depends on the user who makes an assessment of the trust to be assigned to the introducer.
 Certificate trust levels: When a user
Certificate trust levels: When a user A receives a certificate signed by the introducer, it assigns a level of trust to this certificate. Thus, the certificate trust level indicates the extent to which a PGP user can trust the certificate issued by an introducer. It is generally the same as that of the introducer trust level. For example, suppose B issues a certificate for E, and A receives that certificate, then A assigns a full level of trust to this certificate, as A fully trusts B. However, if A receives a certificate from E, then A can either discard this certificate or assign a zero level of trust to it, as A has no trust on E.
 Key legitimacy: This indicates the level of legitimacy of public key of a user. That is, the extent to which one can trust that a particular key is a valid key for a particular user. PGP defines certain weighted trust levels to determine the level of legitimacy of the key for the user. The higher the weight, the stronger the binding of the user ID to his or her key. For example, a weight of 0 indicates a nontrusted certificate, weight of ½ indicates a partially trusted certificate and, finally, a weight of 1 indicates a fully trusted certificate. For example,
Key legitimacy: This indicates the level of legitimacy of public key of a user. That is, the extent to which one can trust that a particular key is a valid key for a particular user. PGP defines certain weighted trust levels to determine the level of legitimacy of the key for the user. The higher the weight, the stronger the binding of the user ID to his or her key. For example, a weight of 0 indicates a nontrusted certificate, weight of ½ indicates a partially trusted certificate and, finally, a weight of 1 indicates a fully trusted certificate. For example, A can use E's public key because B has issued a certificate (with a trust level of 1) for E. However, A cannot use any certificate issued by E, as for A, E has a trust level of none. Thus, it is clear from our example that the legitimacy of the public key of a particular user does not depend on the trust level of that user; rather, it depends on the trust level of the introducer who has issued this certificate.
16. What is the structure of the key rings of PGP? Explain how messages are exchanged with the help of key rings.
Ans.: The structure of a private/public key ring can be represented as a table where each row represents one of the public/private key pairs owned by the user. Each row contains various entries, which are as follows:
 Timestamp: This field specifies the date and time when that particular private/public key pair was generated.
Timestamp: This field specifies the date and time when that particular private/public key pair was generated.
 Key ID: This field contains the least significant 64 bits of the public key for this entry. Since the user can have multiple public keys, this field helps in uniquely identifying each key.
Key ID: This field contains the least significant 64 bits of the public key for this entry. Since the user can have multiple public keys, this field helps in uniquely identifying each key.
 Public key: This field contains the public key portion of the pair.
Public key: This field contains the public key portion of the pair.
 Private key: This is an encrypted field that contains the private key portion of the pair.
Private key: This is an encrypted field that contains the private key portion of the pair.
 User ID: This field generally contains the e-mail address of the user. However, in some cases, the user may wish to associate different names with each pair or to reuse the same user ID.
User ID: This field generally contains the e-mail address of the user. However, in some cases, the user may wish to associate different names with each pair or to reuse the same user ID.
The public key ring contains the public keys of the other users who are known to this user. The fields of the public-key ring are explained as follows:
 Timestamp: This field contains the date and time when the entry was generated.
Timestamp: This field contains the date and time when the entry was generated.
 Key ID: This field contains the least significant 64 bits of the public key for this entry.
Key ID: This field contains the least significant 64 bits of the public key for this entry.
 Public key: This field contains the public key for this entry.
Public key: This field contains the public key for this entry.
 Producer trust: This field specifies the introducer level of trust. It can take one of the three values: none, partial or full.
Producer trust: This field specifies the introducer level of trust. It can take one of the three values: none, partial or full.
 Certificate(s): This field contains one or more certificates signed by other users for this user.
Certificate(s): This field contains one or more certificates signed by other users for this user.
 Certificate Trust(s): This field contains the trust level of certificates. If
Certificate Trust(s): This field contains the trust level of certificates. If A has signed a certificate for B, then the value in the certificate trust field for B is equal to the value in the producer trust field for A.
 Key legitimacy: This field stores a value that is computed on the basis of the value contained in the certificate trust field and the predefined weight for each certificate trust.
Key legitimacy: This field stores a value that is computed on the basis of the value contained in the certificate trust field and the predefined weight for each certificate trust.
 User ID: This field specifies the owner of this public key, and generally contains the e-mail address of the user. There may be more than one user IDs associated with a single public key.
User ID: This field specifies the owner of this public key, and generally contains the e-mail address of the user. There may be more than one user IDs associated with a single public key.
The general structure of private/public ring and public ring is shown in Figure 9.6. Both the private/public and public ring can be indexed by either User ID or Key ID.

Figure 9.6 General Structure of Private/public and Public Ring
To understand the working of key rings, let us suppose that user A wants to send a message to many users and also wants to receive messages from the others. For this, A would have many pairs of private/public keys belonging to him or her and various public keys belonging to the other people with whom he or she wants to communicate. Now, when A wants to send a message to another person in the community, it needs to perform the following steps.
1. A signs the message digest using its private key. The private key of A is retrieved from the private/public key ring using the User ID field as an index.
2. A encrypts a newly created session key using the desired recipient's public key. The public key is retrieved from the public key ring using the User ID of the intended recipient as an index.
3. A encrypts the message and the signed digest using the newly created session key.
When A receives a message from another person in the community, it needs to perform the following steps.
1. A decrypts the session key using its private key. The private key of A is retrieved from the private/public key ring using the Key ID field included in the signature key component as an index.
2. A decrypts the message and the digest using the session key.
3. A verifies the digest using its public key. To retrieve the public key, the Key ID field included in the signature key component is used as an index.
17. What is the need of the Key ID field in the private/public and public key rings in PGP, if the public keys for a user are themselves unique?
Ans.: When a user (say, A) wants to send a message to another user (say, B), then it sends the message and digest encrypted with the session key K. The session key encrypted with the recipient's public key is sent along with the message. However, as in PGP, every user has multiple pairs of private/public keys, then, how does the recipient know which of its public keys has been used for encrypting the session key? One solution is to send the used public key of the recipient along with the message. This approach is fine; however, it results in wastage of space, as public keys are very long. Another solution is to attach a Key ID with each public key, which consists of its least significant 64 bits. The key ID is much shorter than the public key, and uniquely identifies each public key. Now, instead of sending the whole public key, the sender can transmit only the Key ID of the public key. Thus, the Key ID field is included in the private/public and public rings in PGP.
18. Discuss the general format of a PGP message.
Ans.: A PGP message consists of three components: a session key component, a signature and the message (see Figure 9.7). The entire block containing these components is generally encoded with radix-64 encoding. These components are discussed as follows:

Figure 9.7 PGP message format
 Session key component: This component includes the session key and Key ID of the recipient's public key that the sender has used to encrypt the session key.
Session key component: This component includes the session key and Key ID of the recipient's public key that the sender has used to encrypt the session key.
 Signature component: This component includes the following fields.
Signature component: This component includes the following fields.
 Timestamp: This is 4-byte field that defines the time of creation of the signature.
Timestamp: This is 4-byte field that defines the time of creation of the signature.
 Key ID: This is an 8-byte field that contains the Key ID of the signer's public key. This enables the recipient to identify the public key to be used for decrypting the message digest.
Key ID: This is an 8-byte field that contains the Key ID of the signer's public key. This enables the recipient to identify the public key to be used for decrypting the message digest.
 Message digest: This field contains the 160-bit SHA-1 digest, which is computed over the timestamp of the signature along with the data portion of the message component. The inclusion of the timestamp safeguards against replay attacks. The message digest is signed by the sender using its private key.
Message digest: This field contains the 160-bit SHA-1 digest, which is computed over the timestamp of the signature along with the data portion of the message component. The inclusion of the timestamp safeguards against replay attacks. The message digest is signed by the sender using its private key.
 Leading two octets of message digest: This field contains the first 2 bytes of digest in plaintext. These 2 bytes are included as a kind of checksum. These bytes ensure that the recipient is using the correct public key to decrypt the message digest. The recipient compares the plaintext copy of these two octets with the first two octets of the decrypted digest. If they match, it is verified that the recipient is using the correct public key.
Leading two octets of message digest: This field contains the first 2 bytes of digest in plaintext. These 2 bytes are included as a kind of checksum. These bytes ensure that the recipient is using the correct public key to decrypt the message digest. The recipient compares the plaintext copy of these two octets with the first two octets of the decrypted digest. If they match, it is verified that the recipient is using the correct public key.
 Message component: This component contains the actual data to be transmitted. It also includes a filename and a timestamp that specifies the time of creation.
Message component: This component contains the actual data to be transmitted. It also includes a filename and a timestamp that specifies the time of creation.
19. How are PGP certificates different from X.509 certificates?
Ans.: Both PGP and X.509 certificates are standard security certificates. The main differences between PGP and X.509 are discussed in Table 9.3.
| PGP | X.509 |
|---|---|
| PGP certificates contain a self signature, and also support multiple signatures. The public key in a PGP certificate is associated with several fields, which are used to identify the key owner in different ways. | X.509 certificates contain only a single digital signature to verify the key's validity. Moreover, only one field is used for identifying the key owner. |
| PGP certificates can be created by a normal user; no CA is involved in the creation of certificates. The keys are managed by the users, and a user can validate another user. This process eventually results in a web of trust between groups of people. | X.509 certificates have to be issued by a certification authority. The keys here are managed by the CA only. |
| In PGP, multiple paths can exist from fully trusted or partially trusted authorities to any certificate. | In X.509, only a single path exists from the fully trusted authority (CA) to any certificate. |
| In PGP, the certificates can be revoked by the owner of the certificate or the revoker. | In X.509, the certificate can be revoked only by the issuer of the certificate, that is, the CA. |
20. Explain the S/MIME protocol.
Ans.: S/MIME (stands for secure/multipurpose Internet mail extension) is a protocol designed for e-mail that enhances the standard MIME protocol by providing the security features. The S/MIME is similar to PGP as far as IETF standards are concerned, however, it is assumed that, in future, S/MIME is most likely to be used for commercial and organizational purposes, while PGP will be used for personal e-mail security purpose. S/MIME uses the same standards that were used in MIME, along with a few security enhancements. The MIME overview and the S/MIME features are discussed in the following sections.
MIME Overview
MIME (stands for multipurpose Internet mail extensions) is a protocol that enables transferring non-ASCII data through e-mails, and thus, overcomes the limitations of SMTP (simple mail transfer protocol), which only allows sending text messages over the Internet. MIME converts non-ASCII messages to a 7-bit NVT (network virtual terminal) ASCII format at the sender's side. The converted message is then forwarded to the client message transfer agent (MTA), so that it can be sent over the Internet to the receiver. At receiver's side, the message is converted to its original format. MIME can also be used to send messages in different languages such as French, German, Chinese, etc. The structure of MIME defines five new headers that were included in the original e-mail header section. These headers are described as follows.
 MIME-Version: This header specifies the MIME version and tells the receiver that the sender is using MIME message format. The version number 1.1 is being used nowadays.
MIME-Version: This header specifies the MIME version and tells the receiver that the sender is using MIME message format. The version number 1.1 is being used nowadays.
 Content-Type: This header defines the type and subtype of the data used in the message body. The type of the data is followed by its subtype, separated by a slash, that is, type/subtype. Some of the types and their subtypes used by MIME are listed in Table 9.4.
Content-Type: This header defines the type and subtype of the data used in the message body. The type of the data is followed by its subtype, separated by a slash, that is, type/subtype. Some of the types and their subtypes used by MIME are listed in Table 9.4.
| Type | Subtype | Description |
|---|---|---|
| Text | Plain | Unformatted |
| HTML | HTML format | |
| Image | JPEG | Image is in JPEG format |
| GIF | Image is in GIF format | |
| Video | MPEG | Video is in MPEG format |
| Audio | Basic | Single-channel encoding of voice at 8 kHz |
 Content-Transfer-Encoding: This header defines the different methods used in encoding the messages into various formats so that it can be transmitted over a network. Some schemes used for encoding the message body are listed in Table 9.5.
Content-Transfer-Encoding: This header defines the different methods used in encoding the messages into various formats so that it can be transmitted over a network. Some schemes used for encoding the message body are listed in Table 9.5.
| Type | Description |
|---|---|
| 7-bit | NVT ASCII characters and short lines |
| 8-bit | Non-ASCII characters and short lines |
| Binary | Non-ASCII characters with unlimited length |
 Content-Id: This header uniquely identifies the message content.
Content-Id: This header uniquely identifies the message content.
 Content-Description: This header tells what the body of the message contains, that is, whether it contains picture, audio or video. It is an ASCII string that helps the receiver decide whether the message needs to be decoded.
Content-Description: This header tells what the body of the message contains, that is, whether it contains picture, audio or video. It is an ASCII string that helps the receiver decide whether the message needs to be decoded.
S/MIME Functionality
The basic functionality of S/MIME is similar to that of PGP, that is, it mainly supports digital signature and encryption of e-mail messages. However, apart from these basic functionalities, it also supports some other functions, which are as follows.
 Enveloped data: S/MIME supports enveloped data, which consists of the message containing any type of contents in encrypted form and the encryption key encrypted with receiver's public key.
Enveloped data: S/MIME supports enveloped data, which consists of the message containing any type of contents in encrypted form and the encryption key encrypted with receiver's public key.
 Signed data: This consists of the message digest encrypted using the sender's private key. S/MIME provides more confidentiality to the message by encoding the message and the signature using base64 encoding. This signed message can only be viewed by the receivers who have S/MIME capability.
Signed data: This consists of the message digest encrypted using the sender's private key. S/MIME provides more confidentiality to the message by encoding the message and the signature using base64 encoding. This signed message can only be viewed by the receivers who have S/MIME capability.
 Clear-signed data: This functionality is similar to the signed data and forms a digital signature of the message. The only difference is that, in this case, only the digital signature is encoded using base64 encoding. This allows the receivers to view the contents of the message even if they do not have S/MIME capability. However, they cannot verify the signature.
Clear-signed data: This functionality is similar to the signed data and forms a digital signature of the message. The only difference is that, in this case, only the digital signature is encoded using base64 encoding. This allows the receivers to view the contents of the message even if they do not have S/MIME capability. However, they cannot verify the signature.
 Signed and enveloped data: This is a mixture of the previously mentioned functions. In this case, S/MIME allows nesting of signed-only and encrypted-only entities, so that the encrypted data can be signed, and signed or clear-signed data can be encrypted.
Signed and enveloped data: This is a mixture of the previously mentioned functions. In this case, S/MIME allows nesting of signed-only and encrypted-only entities, so that the encrypted data can be signed, and signed or clear-signed data can be encrypted.
S/MIME Messages
S/MIME makes the MIME entity (such as a message or a part of it) secure either with a signature or with encryption, or both. Initially, a MIME entity is prepared according to the general rules for MIME message preparation. The MIME entity can either be the entire message, or a part of it (in case the content type is multipart). Then, the MIME entity along with the security-related data, such as algorithm identifiers and digital certificates, are processed by S/MIME. The output generated from this process is the PKCS (public key cryptography standard) object. The PKCS is now wrapped in MIME, and proper MIME headers are added to it.
To add security features such as digital signatures and encryption, S/MIME defines two new content types, which are listed in Table 9.6.
Table 9.6 S/MIME content types

S/MIME Certificate Processing
S/MIME makes use of digital certificates that conform to the third version of X.509. The key-management scheme of S/MIME is a mixture of X.509 certification hierarchy and PGP's web of trust. As with the PGP model, S/MIME users are responsible for maintaining the certificates needed to verify the incoming signatures and for encrypting the outgoing messages, and as with X.509, only CAs are allowed to sign the certificates.
An S/MIME user performs three key-management functions, namely, key generation, registration and certificate storage and retrieval. In the key generation process, the user having administrative capabilities must be able to generate key pairs using DSS and Diffie-Hellman, and should be able to generate the key pairs using RSA. In the registration process, the user receives an X.509 digital certificate. To receive an X.509 certificate, the user has to first register its public key with the CA. The certificate storage and retrieval process deals with maintaining a local list of certificates, so that the users can retrieve their certificates to validate the incoming signatures and encrypt the outgoing messages. This list can be maintained either by the users or by some local administrative entity on behalf of the users.
S/MIME Enhanced Security Services
The S/MIME provides three enhanced security services, which are discussed as follows:
 Signed receipts: This is an acknowledgement message that is used to inform the sender about the delivery of the message. The entire message, including the original message and signature of the
sender, is signed by the receiver, and the new signature is appended to form a new S/MIME message.
Signed receipts: This is an acknowledgement message that is used to inform the sender about the delivery of the message. The entire message, including the original message and signature of the
sender, is signed by the receiver, and the new signature is appended to form a new S/MIME message.
 Security labels: Each signed object can also include a security label in the authenticated attributes. This security label basically includes information regarding the confidentiality (sensitivity) of the message being protected by S/MIME. In addition to confidentiality, the labels can also be used for access control (which users are authorized to access the object), for defining priority of the message (secret, confidential, restricted, etc.) or for defining role-based access (which category of users are allowed to see the information).
Security labels: Each signed object can also include a security label in the authenticated attributes. This security label basically includes information regarding the confidentiality (sensitivity) of the message being protected by S/MIME. In addition to confidentiality, the labels can also be used for access control (which users are authorized to access the object), for defining priority of the message (secret, confidential, restricted, etc.) or for defining role-based access (which category of users are allowed to see the information).
 Secure mailing lists: When a sender wants to send a message to a recipient, he or she needs to encrypt the message using recipient's public key. In case the same message needs to be sent to several recipients, then the sender has to encrypt the message with every recipient's public key before sending it to these recipients. This is very time-consuming task. To simplify this process, S/MIME provides a Mail List Agent (MLA), who is responsible for performing recipient-specific encryption of the message for each recipient. The creator of the message needs to send the original message to MLA, only once, encrypted with the MLA's public key, and the rest is done by MLA itself.
Secure mailing lists: When a sender wants to send a message to a recipient, he or she needs to encrypt the message using recipient's public key. In case the same message needs to be sent to several recipients, then the sender has to encrypt the message with every recipient's public key before sending it to these recipients. This is very time-consuming task. To simplify this process, S/MIME provides a Mail List Agent (MLA), who is responsible for performing recipient-specific encryption of the message for each recipient. The creator of the message needs to send the original message to MLA, only once, encrypted with the MLA's public key, and the rest is done by MLA itself.
21. Give an overview of IP security along with its applications and benefits.
Ans.: The Internet community has developed many application-specific security protocols such as Kerberos (for client/server), PGP and S/MIME (for electronic mail) and many others. These protocols provide security only at higher network layers, such as the application and transport layer. However, some applications such as routing protocols that use IP services need security service at the network layer or Internet protocol (IP) layer. To provide security at the IP layer, the IETF developed a collection of protocols referred to as IP security (IPSec). Before IPSec was initiated, the IP packets were prone to security failure. The data in the IP packets were in plaintext form, which allowed anyone to access or change the contents of the packets during transmission.
The overall idea of IPSec protocol is to encrypt and seal the transport and application layer during transmission, and also to provide integrity protection in the Internet layer itself. IPSec provides three security functions, namely, authentication, confidentiality and key management. Authentication ensures that the packets are arriving from the actual source as specified in the packet header. It also ensures that the packet has not been altered during transmission. The confidentiality function allows two communicating nodes to transfer messages in an encrypted form in order to prevent any third-party intervention. The key management provides a platform for exchanging keys in a secured manner. All these security measures are incorporated in both the versions of IP, namely, IP version 4 (IPv4) and IP version 6 (IPv6).
The IPSec enables secure communication across different types of networks such as LANs and WANs. It also secures the Internet. The applications of IPSec are discussed as follows:
 Secure remote access over the Internet: An end user using IPSec protocols can make a local call to an Internet Service Provider (ISP) and request it to provide a secure access to a company network. This reduces travelling cost and time wastage of employees and telecommuters.
Secure remote access over the Internet: An end user using IPSec protocols can make a local call to an Internet Service Provider (ISP) and request it to provide a secure access to a company network. This reduces travelling cost and time wastage of employees and telecommuters.
 Enhancing electronic commerce security: Though many e-commerce sites provide in-built security services, the use of IPSec further increases the level of security.
Enhancing electronic commerce security: Though many e-commerce sites provide in-built security services, the use of IPSec further increases the level of security.
 Secure branch office connectivity over the Internet: IPSec can be used to create a secured virtual private network over the Internet or over a public WAN, connecting all the branches of a company. This will save the cost of creating a private network that needs expensive leased lines.
Secure branch office connectivity over the Internet: IPSec can be used to create a secured virtual private network over the Internet or over a public WAN, connecting all the branches of a company. This will save the cost of creating a private network that needs expensive leased lines.
 Establishing extranet and intranet connectivity with partners: IPSec can be used to make secure connections with other organizations, since it addresses all the three security issues: authentication, confidentiality and key management.
Establishing extranet and intranet connectivity with partners: IPSec can be used to make secure connections with other organizations, since it addresses all the three security issues: authentication, confidentiality and key management.
IPSec has got many advantages, which are as follows:
 IPSec is very transparent to end users. There is no need to provide any kind of training to the users. It also does not require to issue or revoke keys to and from the users.
IPSec is very transparent to end users. There is no need to provide any kind of training to the users. It also does not require to issue or revoke keys to and from the users.
 When IPSec is implemented in a firewall or router, it provides more security as it becomes the only entry/exit point for all the traffic. However, the internal traffic does not have to use IPSec and is, thus, free from the overhead of any security-related processing.
When IPSec is implemented in a firewall or router, it provides more security as it becomes the only entry/exit point for all the traffic. However, the internal traffic does not have to use IPSec and is, thus, free from the overhead of any security-related processing.
 Since IPSec is implemented at the network layer, there is no need to make any changes at the upper layers such as application and transport layer.
Since IPSec is implemented at the network layer, there is no need to make any changes at the upper layers such as application and transport layer.
 IPSec can provide security to individual users also. Individuals can set up secure virtual sub-networks within an organization for sensitive applications. These types of connections are useful for offsite workers.
IPSec can provide security to individual users also. Individuals can set up secure virtual sub-networks within an organization for sensitive applications. These types of connections are useful for offsite workers.
22. Write a short note on transport and tunnel mode.
Ans.: IPSec operates in two different modes, namely, transport mode and tunnel mode. The transport mode is used to provide protection mainly for the upper layer protocols. In this mode, IPSec protects the packets coming from the transport layer to the network layer. That is, it only protects the IP layer payload and not the IP header. It does not protect the whole IP packet. In this mode, the IPSec header and IPSec trailer are added to the packet coming from the transport layer, which becomes the IP payload in network layer, and later the IP header is added to the payload. This mode is used for secured host-to-host communication. The sender authenticates and/or encrypts the payload received from the transport layer using IPSec. The receiver verifies the authenticity and/or decrypts the IP packet using IPSec and forwards it to the transport layer.
The tunnel mode is used to provide security to the entire IP packet. Here, the IP packet is totally protected, including the IP header. Also, a new IP header is added to the protected packet. The tunnel mode is used when either or both of the communicating parties are security gateways, such as routers. That is, tunnel mode provides secure communication between two routers, or between a router and a host or between a host and a router. The packets transmitting from sender to receiver are protected from intrusion as if the packets pass through an imaginary tunnel.
The main difference between the transport mode and the tunnel mode is that, in the former case, the IPSec layer comes between the transport layer and the network layer. However, in case of tunnel mode, the information flows from the network layer to the IPSec layer and then back to the network layer.
23. Write a short note on IPSec RFC documents.
Ans.: In 1995, the Internet Engineering Task Force (IETF) published several security standards related to IPSec in the form of RFC documents. The most important of these are RFCs 2401, 2402, 2406, and 2408. RFC 2401 gives an overview of security architecture, RFC 2402 contains a description of a packet authentication extension to IPv4 and IPv6, RFC 2406 consists of a description of a packet encryption extension to IPv4 and IPv6, and finally RFC 2408 includes specification of key management capabilities. In addition to these four RFCs, several additional drafts have been published by IP security Protocol Working Group set up by IETF. These documents are divided into seven groups, as shown in Figure 9.8.

Figure 9.8 Overview of IPSec Document
 Architecture: This includes the general concepts, requirements for security, definitions and the mechanisms needed for defining IP security.
Architecture: This includes the general concepts, requirements for security, definitions and the mechanisms needed for defining IP security.
 Encapsulating security payload (ESP): This includes the packet format and issues related to the use of ESP. The issues deal with the encryption of packets by ESP and, occasionally, with authentication.
Encapsulating security payload (ESP): This includes the packet format and issues related to the use of ESP. The issues deal with the encryption of packets by ESP and, occasionally, with authentication.
 Authentication Header (AH): This includes the packet format and issues related to the use of AH for authentication of packets.
Authentication Header (AH): This includes the packet format and issues related to the use of AH for authentication of packets.
 Encryption algorithm: This is a set of documents describing the use of various encryption algorithms for ESP.
Encryption algorithm: This is a set of documents describing the use of various encryption algorithms for ESP.
 Authentication algorithm: This is a set of documents specifying the use of authentication algorithms for AH. It also deals with the authentication option used in ESP.
Authentication algorithm: This is a set of documents specifying the use of authentication algorithms for AH. It also deals with the authentication option used in ESP.
 Key management: This is a set of documents describing the various key management schemes.
Key management: This is a set of documents describing the various key management schemes.
 Domain of interpretation (DOI): This contains the values that are used to relate all the documents with each other. The values include identifiers for the authentication and encryption algorithms that have already been approved, and operational parameters such as key lifetime.
Domain of interpretation (DOI): This contains the values that are used to relate all the documents with each other. The values include identifiers for the authentication and encryption algorithms that have already been approved, and operational parameters such as key lifetime.
24. Name the two protocols defined by IPSec.
Ans.: The two protocols defined by IPSec are the Authentication Header (AH) protocol and the Encapsulating Security Payload (ESP) protocol. These protocols provide the authentication and/or encryption for the packets at the IP level.
25. Explain the Authentication Header (AH) protocol.
Ans.: The Authentication Header (AH) protocol is used to provide source authentication, and also to ensure the integrity of the payloads being carried in the IP packets.
 The authentication feature allows the receiver to authenticate the sender, and accept or reject packets, accordingly. In addition, it prevents the address spoofing attacks.
The authentication feature allows the receiver to authenticate the sender, and accept or reject packets, accordingly. In addition, it prevents the address spoofing attacks.
 The integrity feature ensures that the contents of the IP packets are not altered during transmission.
The integrity feature ensures that the contents of the IP packets are not altered during transmission.
This protocol is based on the message authentication code (MAC), which implies that the two parties must share a secret key. First, a message digest is created with the help of a hash function and a symmetric key. The message digest is then inserted into the AH. This AH is finally placed in the appropriate location as per the mode used (transport or tunnel). The AH format is shown in the Figure 9.9.

Figure 9.9 Authentication Header format
The various fields of the AH are discussed in the following:
 Next header: This is an 8-bit field that specifies
Next header: This is an 8-bit field that specifies
the type of header immediately following this
header. If ESP header follows the AH, this field contains the value 50, and if another AH follows
this AH, it contains the value 51.
 Payload length: This is an 8-bit field that specifies the length of the AH in 32-bit words (in 4-byte multiples) minus 2. For example, if the length of the authentication data field is 96 bits (or three 32-bit words), then with a three-word fixed length, we have a total of six words in the header. Thus, the value of this field is 4.
Payload length: This is an 8-bit field that specifies the length of the AH in 32-bit words (in 4-byte multiples) minus 2. For example, if the length of the authentication data field is 96 bits (or three 32-bit words), then with a three-word fixed length, we have a total of six words in the header. Thus, the value of this field is 4.
 Reserved field: This is a 16-bit field that has been kept reserved for future use.
Reserved field: This is a 16-bit field that has been kept reserved for future use.
 Security parameter index (SPI): This is a 32-bit field that uniquely identifies the security associations (discussed later) for the traffic to which the IP datagram belongs. It plays the role of a virtual circuit identifier. This field is used in combination with the source and destination addresses, as well as the IPSec protocol used (AH or ESP).
Security parameter index (SPI): This is a 32-bit field that uniquely identifies the security associations (discussed later) for the traffic to which the IP datagram belongs. It plays the role of a virtual circuit identifier. This field is used in combination with the source and destination addresses, as well as the IPSec protocol used (AH or ESP).
 Sequence number: This is a 32-bit field that contains a monotonically increasing number (a counter) that specifies the ordering of the IP datagrams. The sequence number is capable of preventing the replay attacks. The sender must always transmit this field, but the receiver need not always act upon it. The first packet transmitted has a sequence number of 1, and once it reaches the value 232, a new connection must be established and the sender's and receiver's counter must be reset.
Sequence number: This is a 32-bit field that contains a monotonically increasing number (a counter) that specifies the ordering of the IP datagrams. The sequence number is capable of preventing the replay attacks. The sender must always transmit this field, but the receiver need not always act upon it. The first packet transmitted has a sequence number of 1, and once it reaches the value 232, a new connection must be established and the sender's and receiver's counter must be reset.
 Authentication data: This is a variable-length field that contains the authentication data, called the Integrity Check Value (ICV), for the datagram. For IPv4 datagrams, this value must be an integral multiple of 32, and for IPv6, this value must be an integral multiple of 64. The ICV is generated by applying a hash function to the whole IP datagram. The fields that are changed during transmission are not included while applying the hash function.
Authentication data: This is a variable-length field that contains the authentication data, called the Integrity Check Value (ICV), for the datagram. For IPv4 datagrams, this value must be an integral multiple of 32, and for IPv6, this value must be an integral multiple of 64. The ICV is generated by applying a hash function to the whole IP datagram. The fields that are changed during transmission are not included while applying the hash function.
26. How does the AH protocol prevent the replay attack?
Ans.: The sequence number field in the IPSec AH protocol is designed to prevent the replay attacks. Initially, the value of this field is set to 1. Now, each time the sender sends a packet to the receiver over the same security association (or connection), the value is incremented by one. When the value of the sequence reaches 232, it is not set back to 1 in order to prevent the use of the same sequence numbers again. Rather, a new connection with a new secret key must be established between the sender and the receiver.
Since IP is connectionless and unreliable, it does not guarantee that all the packets will be delivered and that the packets will be delivered in the correct sequence. To ensure this, the IPSec authentication document prescribes the receiver to implement a window of size W. The default value of W is 64. The
right edge of the window specifies the highest sequence number N of a valid packet, received so far. After receiving a packet, the receiver takes one of the following actions, depending on the sequence number of the packet:
 The receiver determines whether the received packet is new, and falls in the range of the window, that is, if its sequence number lies between
The receiver determines whether the received packet is new, and falls in the range of the window, that is, if its sequence number lies between N−W+1 and N. If both the conditions are satisfied, then the receiver checks the authenticity of the packet. If the packet is authenticated, the corresponding slot in the window is marked.
 If the sequence number of the newly received packet is greater than
If the sequence number of the newly received packet is greater than N, and if the packet is authenticated, then the receiver advances the window and makes this new sequence number the right edge of the window. Finally, the corresponding slot in the window is marked.
 If the received packet is to the left of the window, that is, its request number is less than
If the received packet is to the left of the window, that is, its request number is less than N−W, or if it is not authenticated, the receiver discards the packet and triggers an auditable event.
The third action prevents the replay attacks, because if the receiver receives a packet with a sequence number less than N−W, then he or she concludes that some attacker is attempting to impersonate the sender and resend an already received packet.
27. Describe how AH is used in transport and tunnel modes in IPSec protocol.
Ans.: The AH protocol can operate in both transport mode and tunnel mode. In transport mode, authentication is provided directly between the server and client workstations. The server and client workstations can be present either on the same network or on different networks. In tunnel mode, a workstation present on a remote network authenticates itself to the corporate firewall. Let us have a look at the scope of authentication provided by AH and the location of AH for the two modes. These two modes further vary for IPv4 and IPv6.
AH Transport Mode
In transport mode AH, when IPv4 packet is used, the AH is inserted after the original IP header but before the IP payload. The entire packet except the mutable fields of IPv4 is authenticated. On the other hand, when IPv6 is used, the AH is inserted after the base header and the hop-by-hop, routing and fragment extension headers. However, the destination options extension header can be placed either before the AH or after it, depending on the desired semantics. The authentication covers the entire IPv6 packet, except the mutable fields. The AH transport mode for both IPv4 and IPv6 packets is shown in Figure 9.10.

Figure 9.10 Transport mode AH
AH Tunnel Mode
In the tunnel mode AH, a new outer IP header is inserted into the packet, and the AH is inserted in between the original IP header and the new outer IP header. The addresses of the original source and destination are included in the inner IP header, while the addresses of firewalls or other security gateways are included in the new outer IP header. AH protects the entire inner IP packet, including the inner IP header. The new outer IP header is also protected, except for the mutable and unpredictable fields. The AH tunnel mode for both IPv4 and IPv6 packets is shown in Figure 9.11.

Figure 9.11 Tunnel mode AH
28. Explain the ESP protocol.
Ans.: The ESP protocol provides confidentiality and integrity of the messages. Optionally, this protocol can also provide an authentication service. The ESP packet format (containing a header and a trailer) is made up of seven fields (see Figure 9.12). These fields are discussed in the following text:
 Security parameters index (SPI): This is a 32-bit field that uniquely identifies the security associations for traffic to which the datagram belongs. It is used in combination with the source and destination IP addresses, as well as the security protocol used (AH or ESP). The SPI value ranges from 1 to 255, and these values have been reserved by the Internet Assigned Numbers Authority (IANA) for future use.
Security parameters index (SPI): This is a 32-bit field that uniquely identifies the security associations for traffic to which the datagram belongs. It is used in combination with the source and destination IP addresses, as well as the security protocol used (AH or ESP). The SPI value ranges from 1 to 255, and these values have been reserved by the Internet Assigned Numbers Authority (IANA) for future use.
 Sequence number: This is a 32-bit field that contains a number that increases monotonically. Initially, counter of both the sender and receiver is set to zero. This field prevents the replay
attacks similar to the AH. The sender must always transmit the field, but the receiver has the freedom to ignore it.
Sequence number: This is a 32-bit field that contains a number that increases monotonically. Initially, counter of both the sender and receiver is set to zero. This field prevents the replay
attacks similar to the AH. The sender must always transmit the field, but the receiver has the freedom to ignore it.

Figure 9.12 IPSec ESP format
 Payload data: This is a variable-length field that contains the transport-layer segment (transport mode) or IP packet (tunnel mode), which is protected using an encryption mechanism.
Payload data: This is a variable-length field that contains the transport-layer segment (transport mode) or IP packet (tunnel mode), which is protected using an encryption mechanism.
 Padding (0–255 bytes): This field contains the padding bits, if any. These bits are mainly used in encryption algorithms for expanding the plaintext to the required length. These can also be used for right-aligning the padding length and next header fields within the 32-bit word. This field also ensures that the ciphertext is an integer multiple of 32 bits.
Padding (0–255 bytes): This field contains the padding bits, if any. These bits are mainly used in encryption algorithms for expanding the plaintext to the required length. These can also be used for right-aligning the padding length and next header fields within the 32-bit word. This field also ensures that the ciphertext is an integer multiple of 32 bits.
 Padding length: This is an 8-bit field that indicates the number of bytes padded in the previous field. It can have a value between 0 and 255. A zero value indicates the absence of any padding bytes. This field is mandatory.
Padding length: This is an 8-bit field that indicates the number of bytes padded in the previous field. It can have a value between 0 and 255. A zero value indicates the absence of any padding bytes. This field is mandatory.
 Next header: This is an 8-bit field that indicates the type of data contained in the payload data field by identifying the first header in that payload (e.g. an upper layer protocol such as TCP in IPv4 and an extension header in IPv6). This field is mandatory.
Next header: This is an 8-bit field that indicates the type of data contained in the payload data field by identifying the first header in that payload (e.g. an upper layer protocol such as TCP in IPv4 and an extension header in IPv6). This field is mandatory.
 Authentication data: This is a variable-length field that contains the Integrity Check Value (ICV). The ICV value is computed by subtracting the authentication data field from the length of the ESP packet. The authentication data must always be an integral multiple of 32-bit words.
Authentication data: This is a variable-length field that contains the Integrity Check Value (ICV). The ICV value is computed by subtracting the authentication data field from the length of the ESP packet. The authentication data must always be an integral multiple of 32-bit words.
29. Describe the transport and tunnel mode of ESP.
Ans.: As with the AH protocol, ESP can also operate in transport and tunnel modes. Considering both IPv4 and IPv6 packets, the working of ESP in transport and tunnel modes is explained in the following:
Transport Mode ESP
The ESP in the transport mode is used to encrypt and optionally authenticate the data carried by IP. In case of IPv4 packets, the ESP header is inserted between the original IP header and transport-layer header (such as TCP, UDP and ICMP). An ESP trailer, consisting of padding, padding length and next header fields, is also placed after the IP packet (see Figure 9.13). If authentication is also used, the ESP authentication data field is also added at the end. The encryption is performed at the entire transport level segment, including the ESP trailer. The ciphertext and the ESP header are then authenticated.

Figure 9.13 Transport mode ESP
In case of IPv6, the ESP header is inserted after the base header and the hop-by-hop, routing and fragment extension headers. Depending on the semantics, the destination options extension header can be inserted either before or after the ESP header. Here, the transport-level segment, the ESP trailer and the destination options extension header (if present) are encrypted, whereas the ciphertext and the ESP header are authenticated.
The operation of ESP transport mode is summarized as follows:
1. At the sender's end, the IP packet is formed by encrypting the plaintext of data containing the ESP trailer and the entire transport-layer segment (TCP header plus data): The authentication can also be added to the IP packet if this option is selected.
2. The packet is transmitted to the destination. The routers falling in the route examine and process only the IP header and the plaintext IP extension headers (if present) and not the ciphertext.
3. When the IP packet is received by the destination, the IP header and the plaintext IP extension headers are processed. After this, the destination decrypts the rest of the packet based on SPI in the ESP header in order to retrieve the plaintext transport layer segment.
Tunnel Mode ESP
In tunnel mode ESP, the entire IP packet is encrypted. The ESP header is prefixed to the packet, and the packet is then encrypted including the ESP trailer (see Figure 9.14). In this mode, the entire block (ESP header, ciphertext and authentication data, if present) is encapsulated with a new IP header because the original IP header contains the destination address and possibly intermediate routing information and, thus, cannot be transmitted as it is. Therefore, a new IP header is needed that will contain the necessary information for routing and not for traffic analysis.
The difference between transport mode ESP and tunnel mode ESP is that the former is used to protect connections between two hosts supporting the ESP feature, while the latter is suitable for protecting connections in configurations when some sort of security gateway or firewall is used. The encryption process in the tunnel mode involves only the external hosts and security gateways. The hosts on the internal network are not involved in this process, thus relieving them from the extra burden of encryption. This makes the key distribution task simpler, as lesser number of keys would be required, and prevents traffic analysis based on the ultimate destination.

Figure 9.14 Tunnel Mode ESP
The operation of the ESP tunnel mode is summarized as follows.
1. At the sender's end, the inner IP packet is prepared using the destination address of the target host on the internal network. The ESP header is prepended to the packet. The packet and ESP trailer are then encrypted, and authentication data is added (if required) to form a block. The block is encapsulated with a new IP header that consists of the base header and some other extension headers such as routing and hop-by-hop options. This forms the outer IP packet, which contains the destination address of a firewall.
2. The outer IP packet is forwarded to the destination firewall. The routers falling in the route examine and process only the IP header and the plaintext IP extension headers (if present) and not the ciphertext.
3. At the receiver's end (i.e., firewall), the IP header and the plaintext IP extension headers are processed once again by the destination firewall. The ciphertext is then decrypted on the basis of SPI in the ESP header to recover the plaintext inner packet.
4. The inner packet is routed through zero or more routers in the internal network to reach the destination host.
30. Explain the Internet Key Exchange protocol and security association.
Ans.: Internet Key Exchange (IKE) is another supporting protocol that is used for the key management procedures in IPSec. It is the first phase of IPSec, where the cryptographic algorithms and keys to be later used by AH and ESP are decided. After the IKE phase, actual AH and ESP operations are carried over. The output of the IKE phase is Security Association (SA), which is a logical relationship agreement between the sender and receiver that allows both the communication parties to agree upon some factors such as IPSec protocol version in use, mode of operation (transport or tunnel mode), cryptographic algorithms and keys, lifetime of keys, etc.
The main objective of IKE is to build an SA between the sender and the receiver, which is further used by AH and ESP for their actual operation. Note that in case both AH and ESP are in use, then each communicating party requires two sets of SA: one for AH and other for ESP. Moreover, SA allows only one-way communication, and hence, the communicating parties require two more sets of SA; one for incoming messages and other for outgoing messages. Thus, in total, they require four sets of SA, if both AH and ESP are in use.
31. What are the services provided by IPSec?
Ans.: The services provided by IPSec are as follows:
 Access control
Access control
 Connectionless integrity
Connectionless integrity
 Data origin authentication
Data origin authentication
 Rejection of replayed packets
Rejection of replayed packets
 Confidentiality
Confidentiality
 Limited traffic flow confidentiality
Limited traffic flow confidentiality
The AH and ESP protocols of IPSec are responsible for providing some or all of these services. The AH protocol provides the first four services, that is, access control, connectionless integrity, data origin authentication and rejection of replayed packets. However, for ESP protocol, there are two cases, which are as follows:
 If the ESP protocol allows encryption only, then it provides access control, rejection of replayed packets, confidentiality and limited traffic flow confidentiality.
If the ESP protocol allows encryption only, then it provides access control, rejection of replayed packets, confidentiality and limited traffic flow confidentiality.
 If the ESP protocol allows both encryption and authentication, then it provides all these services.
If the ESP protocol allows both encryption and authentication, then it provides all these services.
32. Describe the features of Oakley algorithm used for key determination in IPSec.
Ans.: The Oakley algorithm is a key exchange protocol developed by Hilarie Orman. It is based on Diffie-Hellman algorithm, and is designed to retain the advantages of Diffie-Hellman while overcoming its limitations. Oakley is a free-formatted protocol, in the sense that it does not define any specific format for the message to be transmitted. It also provides more security than Diffie-Hellman algorithm. There are five features in Oakley algorithm that are used for key determination. These features are discussed in the following text:
 The clogging attack encountered in the Diffie-Hellman algorithm is removed in Oakley using the cookie mechanism. In this attack, the victim's system is clogged with useless work as it remains busy in generating secret keys for forged public keys sent by the intruder. In cookie exchange mechanism, a pseudo-random number, called a cookie, is generated by applying a hash function (such as MD5) over the source and destination address, the UDP source and destination ports, and a locally generated secret value. The cookie is sent from each side in the initial message, which is acknowledged by the other side. This acknowledgement must be repeated in the first message of the Diffie-Hellman key exchange. If the source address was forged, the intruder gets no answer. Thus, the intruder can only force a user to generate acknowledgements and not to perform useless calculations.
The clogging attack encountered in the Diffie-Hellman algorithm is removed in Oakley using the cookie mechanism. In this attack, the victim's system is clogged with useless work as it remains busy in generating secret keys for forged public keys sent by the intruder. In cookie exchange mechanism, a pseudo-random number, called a cookie, is generated by applying a hash function (such as MD5) over the source and destination address, the UDP source and destination ports, and a locally generated secret value. The cookie is sent from each side in the initial message, which is acknowledged by the other side. This acknowledgement must be repeated in the first message of the Diffie-Hellman key exchange. If the source address was forged, the intruder gets no answer. Thus, the intruder can only force a user to generate acknowledgements and not to perform useless calculations.
 The Oakley algorithm allows two parties to negotiate a group for specifying global parameters of Diffie-Hellman key exchange. Oakley supports the use of different groups for the Diffie-Hellman key exchange, where each group specifies the two global parameters (one is
The Oakley algorithm allows two parties to negotiate a group for specifying global parameters of Diffie-Hellman key exchange. Oakley supports the use of different groups for the Diffie-Hellman key exchange, where each group specifies the two global parameters (one is p, a large prime number and second is q, a primitive root of p), and the identity of the Diffie-Hellman algorithm. The present specification includes five groups, which are as follows:
 Modular exponentiation with a 768-bit modulus
Modular exponentiation with a 768-bit modulus
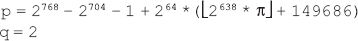
 Modular exponentiation with a 1024-bit modulus
Modular exponentiation with a 1024-bit modulus
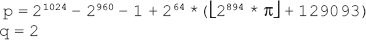
 Modular exponentiation with a 1536-bit modulus
Modular exponentiation with a 1536-bit modulus
– Parameters to be determined
 Elliptic curve group over 2155
Elliptic curve group over 2155
– Generator (hexadecimal): X = 7B, Y = 1C8.
– Elliptic curve parameters (hexadecimal): A = 0, Y = 7338F
 Elliptic curve group over 2185
Elliptic curve group over 2185
– Generator (hexadecimal): X = 18, Y = D
– Elliptic curve parameters (hexadecimal): A = 0, Y = 1EE9
 The Oakley algorithm prevents replay attacks by using nonces. The nonce is a pseudo-random number that is generated locally. Nonces are included in response messages, and are encrypted during certain portion of the exchange to secure their use.
The Oakley algorithm prevents replay attacks by using nonces. The nonce is a pseudo-random number that is generated locally. Nonces are included in response messages, and are encrypted during certain portion of the exchange to secure their use.
 The Oakley algorithm facilitates the exchange of Diffie-Hellman public key values (discussed in Chapter 5).
The Oakley algorithm facilitates the exchange of Diffie-Hellman public key values (discussed in Chapter 5).
 The Oakley algorithm authenticates the Diffie-Hellman exchange to prevent man-in-the-middle attacks. It can apply various authentication mechanisms such as digital signatures, public-key encryption and symmetric-key encryption on some important parameters such as user IDs and nonces to authenticate the key exchange.
The Oakley algorithm authenticates the Diffie-Hellman exchange to prevent man-in-the-middle attacks. It can apply various authentication mechanisms such as digital signatures, public-key encryption and symmetric-key encryption on some important parameters such as user IDs and nonces to authenticate the key exchange.
33. Explain the header format for an ISAKMP message.
Ans.: Internet Security Association and Key Management Protocol (ISAKMP) is designed to carry messages for Internet key exchange in IPSec. It defines procedures and formats for establishing, maintaining and deleting information regarding security associations. An ISAKMP message consists of an ISAKMP header followed by one or more payloads. This entire block is encapsulated inside a transport segment (such as a TCP segment). The header format for an ISAKMP message is shown in Figure 9.15. It consists of the following fields.

Figure 9.15 ISAKMP header format
 Initiator cookie: This is a 64-bit field
Initiator cookie: This is a 64-bit field
defining the cookie of the entity that initiates
the SA establishment, notification or deletion.
 Responder cookie: This is also a 64-bit field defining the cookie of the entity responding to the initiator. This field contains the value 0 in the first message sent by the initiator.
Responder cookie: This is also a 64-bit field defining the cookie of the entity responding to the initiator. This field contains the value 0 in the first message sent by the initiator.
 Next payload: This is an 8-bit field indicating the type of the first payload of the message.
Next payload: This is an 8-bit field indicating the type of the first payload of the message.
 Major version: This is a 4-bit field indicating the major ISAKMP version as used in the current exchange. The current value of this field is 1.
Major version: This is a 4-bit field indicating the major ISAKMP version as used in the current exchange. The current value of this field is 1.
 Minor version: This is also a 4-bit field indicating the minor ISAKMP version as used in the current exchange. The current value of this field is 0.
Minor version: This is also a 4-bit field indicating the minor ISAKMP version as used in the current exchange. The current value of this field is 0.
 Exchange type: This is an 8-bit field indicating the type of exchange that is being carried by the ISAKMP packets.
Exchange type: This is an 8-bit field indicating the type of exchange that is being carried by the ISAKMP packets.
 Flags: This is an 8-bit field indicating the specific set of options for this ISAKMP exchange. Each bit in this field defines a single option. So far, only 3 bits have been defined, which are as follows.
Flags: This is an 8-bit field indicating the specific set of options for this ISAKMP exchange. Each bit in this field defines a single option. So far, only 3 bits have been defined, which are as follows.
 Encryption bit is set to 1, if all the payloads following the header are encrypted using the encryption algorithm for this SA.
Encryption bit is set to 1, if all the payloads following the header are encrypted using the encryption algorithm for this SA.
 Commit bit is set to 1 to ensure that the encrypted packet is not received until the SA is established.
Commit bit is set to 1 to ensure that the encrypted packet is not received until the SA is established.
 Authentication bit is set to 1 to ensure that the rest of the payload, which is not encrypted, is still authenticated for integrity.
Authentication bit is set to 1 to ensure that the rest of the payload, which is not encrypted, is still authenticated for integrity.
 Message ID: This is a 32-bit field specifying a unique ID for this message.
Message ID: This is a 32-bit field specifying a unique ID for this message.
 Message length: This is a 32-bit field specifying the total length of the packet (including the header and all payloads) in octets.
Message length: This is a 32-bit field specifying the total length of the packet (including the header and all payloads) in octets.
34. What is SSL? Discuss its architecture.
Ans.: The Secure Socket Layer (SSL) protocol was developed by Netscape Corporation in 1994 to provide exchange of information between a web browser and a web server in a secure manner. As with other protocols, its main aim is to provide entity authentication, message integrity and confidentiality. SSL is an additional layer located between the application layer and the transport layer of the TCP/IP protocol suite. All the major web browsers support SSL. It comes in three versions: 2, 3 and 3.1. Among these, version 3, which was released in 1995, is the most popular version.
SSL architecture
SSL is not a single protocol; rather, it is two layers of protocols, as shown in Figure 9.16. The higher-layer protocols include Handshake protocol, Change Cipher Spec protocol and Alert protocol. These three protocols are defined as part of SSL, and are used in the SSL management process. The lower layer includes the SSL Record protocol, which is used for providing various basic security services to the higher-layer protocols. HTTP, which enables the web browser to interact with the web server, can work on the top of SSL.

Figure 9.16 SSL Architecture
These protocols are discussed as follows:
 SSL Record protocol: This protocol acts as a carrier. That is, it is used for carrying the messages from the higher-layer protocols as well as data coming from the application layer. It receives the data to be transmitted from the application layer, and operates on it as follows:
SSL Record protocol: This protocol acts as a carrier. That is, it is used for carrying the messages from the higher-layer protocols as well as data coming from the application layer. It receives the data to be transmitted from the application layer, and operates on it as follows:
1. Fragmentation: The data is first divided into the blocks of 214 bytes or less.
2. Compression: This is an optional phase in which each fragment of data is compressed using one of the lossless compression techniques agreed upon between the client and server.
3. Message integrity: A keyed-hash function is applied on the compressed data to compute a message authentication code (MAC). This ensures the integrity of the message.
4. Confidentiality: The original data and the MAC are encrypted using symmetric-key cryptography to ensure confidentiality.
5. Framing: Finally, an SSL header is added to the encrypted payload, which is then transmitted to a reliable transport layer protocol.
 Handshake protocol: This protocol is the most complex part of SSL. It allows authentication between the server and the client. It allows the server and the client to negotiate on an encryption and MAC algorithm, and cryptographic keys to be used for encrypting the data in an SSL record. In this protocol, several messages are exchanged between the server and the client. All of these messages have a fixed format with three fields [see Figure 9.17(a)], as listed in the following:
Handshake protocol: This protocol is the most complex part of SSL. It allows authentication between the server and the client. It allows the server and the client to negotiate on an encryption and MAC algorithm, and cryptographic keys to be used for encrypting the data in an SSL record. In this protocol, several messages are exchanged between the server and the client. All of these messages have a fixed format with three fields [see Figure 9.17(a)], as listed in the following:
 Type: This is a 1-byte field indicating one of the ten possible message types. The ten message types are hello_request, client_hello, server_hello, certificate, server_key_exchange, certificate_request, server_done, certificate_verify, client_key_exchange and finished.
Type: This is a 1-byte field indicating one of the ten possible message types. The ten message types are hello_request, client_hello, server_hello, certificate, server_key_exchange, certificate_request, server_done, certificate_verify, client_key_exchange and finished.
 Length: This is a 3-byte field specifying the length of the message in bytes.
Length: This is a 3-byte field specifying the length of the message in bytes.
 Content: This field contains the parameters associated with this message, depending on the message type. For example, in case of hello_request and server_done messages, the parameter list is null. In case of certificate message, the parameter list contains a list of X.509v3 certificates.
Content: This field contains the parameters associated with this message, depending on the message type. For example, in case of hello_request and server_done messages, the parameter list is null. In case of certificate message, the parameter list contains a list of X.509v3 certificates.
The Handshake protocol consists of four phases. These phases are:
1. Establish security capabilities: In this phase, a logical connection is initiated and the security capabilities associated with that connection are established. This is done with the help of two messages, the client_hello and server_hello.
2. Server authentication and key exchange: This phase is initiated by the server. In this phase, the server is authenticated to the client, and the client is made aware of the public key of the server if needed. In this phase, only the server sends the messages, while the client only receives the messages. The messages used in this phase are: certificate, server_key_exchange, certificate_request and server_done.
3. Client authentication and key exchange: This phase is initiated by the client. In this phase, the client is authenticated to the server, and both the client and server know the pre-master secret. In this phase, the client sends the messages, and the server only receives the messages. The messages used in this phase are: certificate, client_key_exchange, certificate_request and certificate_verify.
4. Finish: This is last phase in the SSL handshake protocol, which completes the setting up of a secure connection. It is initiated by the client and terminated by the server. First, two messages, change_cipher_spec and finished, are sent by the client, and then the server responds with two similar messages change_cipher_spec and finished message.
 Change cipher spec protocol: Once the server and the client have negotiated on the cryptographic secrets during the Handshake protocol, the next step is to use these secrets. The change cipher spec is the simplest protocol that is used to signal that the cryptographic secrets are ready for use. This protocol consists of only one message, which consists of a single byte with the value 1 [see Figure 9.17(b)]. This value causes the pending state to be changed to the active state. The pending state is the one in which two communicating parties keep track of the parameters and secrets. The active state is the one in which the two parties use these parameters and secrets to sign/verify or encrypt/decrypt the messages. The change cipher spec protocol is responsible for moving values between the pending state and active state.
Change cipher spec protocol: Once the server and the client have negotiated on the cryptographic secrets during the Handshake protocol, the next step is to use these secrets. The change cipher spec is the simplest protocol that is used to signal that the cryptographic secrets are ready for use. This protocol consists of only one message, which consists of a single byte with the value 1 [see Figure 9.17(b)]. This value causes the pending state to be changed to the active state. The pending state is the one in which two communicating parties keep track of the parameters and secrets. The active state is the one in which the two parties use these parameters and secrets to sign/verify or encrypt/decrypt the messages. The change cipher spec protocol is responsible for moving values between the pending state and active state.

Figure 9.17 Message Format of SSL Protocols
 Alert protocol: This protocol is used to signal errors or any abnormal conditions to the nodes. It enables the nodes to exchange the error or warning information. The type of message associated with alert protocol is the Alert message. There are two bytes in each message of the alert protocol [see Figure 9.17(c)]. The first byte conveys the severity of the error. It can take either the value 1 or 2, where value 1 indicates warning and value 2 indicates fatal. In case of fatal error, the connection is immediately terminated. The second byte contains a code that indicates the specific alert. Some of the possible alert codes are unexpected_message, handshake_failure, decompression_failure, no_certificate, certificate_revoked and certificate_expired.
Alert protocol: This protocol is used to signal errors or any abnormal conditions to the nodes. It enables the nodes to exchange the error or warning information. The type of message associated with alert protocol is the Alert message. There are two bytes in each message of the alert protocol [see Figure 9.17(c)]. The first byte conveys the severity of the error. It can take either the value 1 or 2, where value 1 indicates warning and value 2 indicates fatal. In case of fatal error, the connection is immediately terminated. The second byte contains a code that indicates the specific alert. Some of the possible alert codes are unexpected_message, handshake_failure, decompression_failure, no_certificate, certificate_revoked and certificate_expired.
35. What are the differences between an SSL connection and an SSL session?
Ans.: The differences between an SSL connection and an SSL session are discussed in the following:
A session is established between a client and a server, while a connection is established between two peers having equal roles.
 A session can consist of many connections, while a connection is associated with only one session.
A session can consist of many connections, while a connection is associated with only one session.
 A connection can be terminated and re-established within the same session. When a connection is terminated, the session between the two parties may or may not be terminated. However, when the session is terminated, all the connections of that session also terminate. A session may be suspended or resumed again.
A connection can be terminated and re-established within the same session. When a connection is terminated, the session between the two parties may or may not be terminated. However, when the session is terminated, all the connections of that session also terminate. A session may be suspended or resumed again.
 Data can be exchanged only when the connection between the two parties is established; mere establishment of session is not enough for exchange of data.
Data can be exchanged only when the connection between the two parties is established; mere establishment of session is not enough for exchange of data.
 To create a new session, the communicating parties have to go through a negotiation process. However, to create a new connection within the same session, the negotiation process can be skipped.
To create a new session, the communicating parties have to go through a negotiation process. However, to create a new connection within the same session, the negotiation process can be skipped.
36. Describe briefly the TLS protocol. Also, differentiate between the SSL and TLS protocols.
Ans.: The Transport Layer Security (TLS) protocol is the Internet standard version of the SSL protocol by IETF. Netscape wanted to have a standardized version of SSL, and hence handed over it to IETF. The core idea and implementation of both the protocols are quite similar; however, there are some minor differences. These differences are listed in Table 9.7.
| Property | SSL | TLS |
|---|---|---|
| Version | The commonly used version of SSL is 3.0. | The current version of TLS is 1.0. |
| Cipher suite | An algorithm called Fortezza is used. | The algorithm Fortezza is not used. |
| Cryptography secret | It uses the standard SSL encryption to create a master secret. | A pseudorandom function (PRF) is used to create a master secret. |
| Alert protocol | It uses the standard SSL alert protocol. | The no_certificate alert message is not supported. Some new messages are added, such as decryption_failed, record_overflow, access_denied, unknown_CA, export_restriction, decode_error, protocol_version, insufficient_security and internal_error. |
| Handshake protocol | It uses the standard SSL handshake protocol. | The details of the certificate_verify message and finished message are changed. |
| Record protocol | Uses MAC | Uses HMAC |
37. What is SET? How does SET work? Also, discuss the dual signature for SET and its purpose.
Ans.: The Secure Electronic Transaction (SET) protocol is used for secured credit card transactions over the Internet. SET itself is not a payment system; rather, it contains the security protocols and formats that are used to provide security to the credit card payments made by a user on a public network such as the Internet. The SET concept was started as early as the year 1996, but the first product came to be available only in the year 1998. SET mainly provides three services, which are as follows:
 It provides a secured medium of communication for all the parties involved in a communication.
It provides a secured medium of communication for all the parties involved in a communication.
 It provides trust by the use of X.509v3 digital certificates.
It provides trust by the use of X.509v3 digital certificates.
 It provides complete privacy as the parties involved in the communication can access the information only when and where necessary.
It provides complete privacy as the parties involved in the communication can access the information only when and where necessary.
To understand the working of SET, it is important to know the participants of the SET system. The main participants of SET system are:
 Cardholder: The person who owns the card (such as MasterCard, Visa) and does the purchasing on the Internet.
Cardholder: The person who owns the card (such as MasterCard, Visa) and does the purchasing on the Internet.
 Merchant: The organization or the individual who sells goods or offers services to the cardholder. Usually, these goods and services are offered via a website.
Merchant: The organization or the individual who sells goods or offers services to the cardholder. Usually, these goods and services are offered via a website.
 Issuer: The financial institutions (such as banks) that issue the credit cards and are responsible for the payment of purchases made by the cardholder.
Issuer: The financial institutions (such as banks) that issue the credit cards and are responsible for the payment of purchases made by the cardholder.
 Acquirer: This is also a financial institution that is responsible for establishing an account with the merchant and processing payment card authorizations and payments. Generally, a merchant accepts many credit cards issued by different banks. Since the merchant cannot deal with all the banks, or it cannot have account in all the banks, therefore, it needs an acquirer who provides authorization to the merchant that the card account is valid and active. The acquirer also transfers the payments electronically to the merchant's account. The issuer subsequently reimburses the acquirer over some kind of payment network for electronic funds transfer.
Acquirer: This is also a financial institution that is responsible for establishing an account with the merchant and processing payment card authorizations and payments. Generally, a merchant accepts many credit cards issued by different banks. Since the merchant cannot deal with all the banks, or it cannot have account in all the banks, therefore, it needs an acquirer who provides authorization to the merchant that the card account is valid and active. The acquirer also transfers the payments electronically to the merchant's account. The issuer subsequently reimburses the acquirer over some kind of payment network for electronic funds transfer.
 Acquirer payment gateway: This is an interface between SET and the computer networks of banks for authorization and payment functions.
Acquirer payment gateway: This is an interface between SET and the computer networks of banks for authorization and payment functions.
 Certification authority (CA): This is an organization that offers different classes of certificates for cardholders, merchants and payment gateways.
Certification authority (CA): This is an organization that offers different classes of certificates for cardholders, merchants and payment gateways.
Working of SET
Before using SET, both the cardholder and the merchant must register with the CA. After the registration process, the working of SET involves many steps, which are as follows:
1. The customer browses the merchant's website to evaluate the products offered by the merchant. He or she then selects the products to be purchased and adds them to the shopping cart.
2. The customer then uses a single message to communicate with the merchant and payment gateway. The message has two parts, namely, purchase order, which is used by the merchant, and card information, which is used by the merchant's bank (acquirer).
3. The card information is then forwarded to the acquirer.
4. The acquirer contacts the issuer and checks about payment authorization.
5. If the purchase is authorized, the issuer sends the authorization to the acquirer.
6. A copy of the authorization is also forwarded to the merchant.
7. The merchant completes the order and informs the customer about it.
8. Merchant captures the transaction from its bank.
9. Finally, the credit card invoice is printed by the issuer and provided to the customer.
Dual Signatures
As stated in step 2 of SET, the customer uses a single message to communicate with the merchant and the payment gateway. Therefore, the customer has to ensure that the merchant will not be able to view the payment instruction, and that the acquirer will not be able to view the order instruction. Also, the order and payment has to be linked together, so that the customer can prove that the payment is for the particular order. This whole process is implemented using a concept known as dual signature. The creation of dual signature involves five steps, which are as follows:
1. The customer creates the Payment Information Message Digest (PIMD) by taking the hash (using SHA-1) of the Payment Information (PI).
2. The customer creates another digest, that is, the Order Information Message Digest (OIMD) by taking the hash (again using SHA-1) of the Order Information (OI).
3. Both the PIMD and OIMD are combined together.
4. The combined result is again passed through the hash algorithm SHA-1, and a new digest, Payment Order Message Digest (POMD), is created.
5. Finally, the customer encrypts the POMD with his or her private key using the RSA algorithm, thereby creating the dual signature (DS). This POMD is available to both the merchant and the payment gateway.
Now, the cardholder sends OI, DS and PIMD to the merchant. The merchant verifies that the order information has come from the cardholder, and not from any imposter, by following these steps:
1. The merchant computes its own OIMD by taking hash of OI.
2. The PIMD received from the customer and the computed OIMD are then combined to form a new POMD (say, POMD1).
3. The merchant decrypts the received DS to recover the original POMD.
4. The merchant then compares POMD and POMD1. If both are equal, the message is accepted; otherwise, it is rejected.
Similarly, the payment gateway receives PI, DS and OIMD from the cardholder. Then, it verifies that the payment information has come from the cardholder and not from anyone else. For this, it uses a similar process as used by the merchant to verify the order information. To protect the payment information from the merchant, the cardholder encrypts PI, DS and OIMD with one-time session key K. The key K is also encrypted with the private key of the payment gateway. These two together form a digital envelope, which is sent to the merchant. The merchant is supposed to send this envelope to the payment gateway. Since the merchant does not know the public key of the payment gateway, it cannot decrypt the envelope to obtain the payment details. The payment gateway verifies the authenticity of the cardholder by following these steps.
1. The payment gateway computes its own PIMD by taking hash of PI.
2. The OIMD received from the customer and the computed PIMD are then combined to form a new POMD (say, POMD1).
3. The payment gateway decrypts the received DS to recover the original POMD.
4. The payment gateway then compares the POMD and POMD1. If both are equal, it is verified that the message has come from the cardholder, and not from any imposter.
38. Differentiate between SSL and SET.
Ans.: SSL and SET are both Internet security protocols. However, they differ in some aspects as SET is more secured than SSL. The authentication mechanism used in SET is very complex, which makes it almost impossible for both the sender and receiver to commit any kind of fraud. In a nutshell, SET has been specifically designed for secured e-commerce transactions involving online payments, while SSL has been designed only for exchanging messages over the Internet. The main differences between SSL and SET are listed in the Table 9.8.
| Issue | SSL | SET |
|---|---|---|
| Main objective | To allow exchange of data in an encrypted form | To support e-commerce-related payment mechanisms |
| Certification | The certificates are exchanged between the two parties. | A trusted third party certifies all the parties involved in the communication process. |
| Authentication | The authentication mechanism is not very strong. | The authentication mechanism is very strong. |
| Risk of merchant fraud | It is prone to merchant fraud as financial data is provided to the merchant. | It is free from this fraud as financial data is given to the payment gateway only. |
| Risk of customer fraud | It is prone to this kind of fraud as the customer can refuse to pay later; there is no mechanism that can prevent such kind of fraud. | The payment instructions are digitally signed by the customer. Thus, there is less chance of such fraud. |
| Action in case of customer fraud | Merchant is responsible if a customer later refuses to pay | Payment gateway is responsible in case of customer fraud. |
| Practical usage | High | Less |
Multiple-choice Questions
1. Which server acts as KDC in the Kerberos protocol?
(a) TGS
(b) AS
(c) Real server
(d) None of these
2. Which encryption algorithm is used in the Kerberos 4 protocol?
(a) AES
(b) Block cipher
(c) DES
(d) Triple DES
3. In which year was X.509 first issued?
(a) 1988
(b) 1978
(c) 1982
(d) 1994
4. Who issues the PGP certificates?
(a) ITU-T
(b) IEEE
(c) IETF
(d) The users themselves
5. What are the two modes that IPSec protocol works on?
(a) On and Off
(b) Transport and Tunnel
(c) Forward and Backward
(d) Linked and Unlinked
6. Which of the following are IPSec protocols?
(a) PGP and S/MIME
(b) Kerberos 4, Kerberos 5
(c) AH and ESP
(d) SSL and SET
7. Which algorithm solves the man-in-the-middle attack problem?
(a) Diffie-Hellman
(b) RSA
(c) Oakley
(d) ISAKMP
8. Which of the following Internet security protocols is used for secure credit card payments?
(a) SET
(b) PGP
(c) SSL
(d) TLS
9. The _________ protocol uses the Fortezza algorithm.
(a) TLS
(b) SET
(c) ESP
(d) SSL
10. In which protocol is the payment gateway used?
(a) SET
(b) PGP
(c) TLS
(d) SSL
Answers
1. (b)
2. (c)
3. (a)
4. (d)
5. (b)
6. (c)
7. (c)
8. (a)
9. (d)
10.(a)
1. What do you mean by the term intruders? Explain intrusion techniques in brief.
Ans.: Intruders are the attackers who attempt to breach the security of a network. They attack the network in order to get unauthorized access. Intruders are of three types, namely, masquerader, misfeasor and clandestine user.
 Masquerader is an external user who is not authorized to use a computer, and yet tries to gain privileges to access a legitimate user's account. Masquerading is generally done either using stolen IDs and passwords, or through bypassing authentication mechanisms.
Masquerader is an external user who is not authorized to use a computer, and yet tries to gain privileges to access a legitimate user's account. Masquerading is generally done either using stolen IDs and passwords, or through bypassing authentication mechanisms.
 Misfeasor is a legitimate user who either accesses some applications or data without sufficient privileges to access them, or has privilege to access them, but misuses these privileges. A misfeasor is generally an internal user.
Misfeasor is a legitimate user who either accesses some applications or data without sufficient privileges to access them, or has privilege to access them, but misuses these privileges. A misfeasor is generally an internal user.
 Clandestine user is either an internal or external user who gains administrative control of the system and tries to avoid access control and auditing information.
Clandestine user is either an internal or external user who gains administrative control of the system and tries to avoid access control and auditing information.
Intrusion Techniques
The intruders always indulge in finding some way to gain access to the system or to increase the number of privileges assigned to them. To do this, the intruders need access to information that should have been protected, such as some legitimate user's password. After learning the password of an authorized user, intruders can use it to log on to the system and misuse the privileges assigned to the authorized user. Some techniques that the intruders can use to learn others' passwords are as listed here:
 They can try the passwords that are by default assigned to standard accounts such as administrator, as it is possible that the administrators may not change their passwords.
They can try the passwords that are by default assigned to standard accounts such as administrator, as it is possible that the administrators may not change their passwords.
 They can thoroughly test all the short passwords made up of one, two or three characters.
They can thoroughly test all the short passwords made up of one, two or three characters.
 They can intercept the communication between the host system and a remote user.
They can intercept the communication between the host system and a remote user.
 They can use a malicious program, such as a Trojan horse, to get around the restrictions imposed on access.
They can use a malicious program, such as a Trojan horse, to get around the restrictions imposed on access.
 They can try the words that are available in the system's online dictionary or that are expected to be used.
They can try the words that are available in the system's online dictionary or that are expected to be used.
 They can try the users' personal information such as their IDs, phone numbers, room numbers, names of their spouses and children, birthdates, etc.
They can try the users' personal information such as their IDs, phone numbers, room numbers, names of their spouses and children, birthdates, etc.
Besides learning passwords, the intruders can go for other ways to gain access to the system or to gain further privileges. For example, they can exploit attacks such as buffer overflows on a program that executes with certain privileges.
2. Discuss password protection approaches.
Ans.: Generally, passwords are stored by the system in a password file along with the user IDs. Thus, to protect passwords from being captured by the intruders, it is necessary to protect the password file. There are two ways to protect the password file, as listed here:
 One-way function: The system does not store the passwords in a clear form in the password file; rather, it applies a function on the user's password and stores the resulting value in the password file. Whenever a user attempts to log on to the system with the help of his or her user ID and password, the system applies the same function on the supplied password. Then it checks whether the newly computed value matches with the stored value. If so, the user is authenticated and allowed access; otherwise, access is denied. The advantage of using this method of protecting the password file is that even if an intruder gets access to the password file, he or she will not be able to get the passwords.
One-way function: The system does not store the passwords in a clear form in the password file; rather, it applies a function on the user's password and stores the resulting value in the password file. Whenever a user attempts to log on to the system with the help of his or her user ID and password, the system applies the same function on the supplied password. Then it checks whether the newly computed value matches with the stored value. If so, the user is authenticated and allowed access; otherwise, access is denied. The advantage of using this method of protecting the password file is that even if an intruder gets access to the password file, he or she will not be able to get the passwords.
 Access control: Another means of protecting the password file is by restricting access to the password file. Only a few users such as the system administrator must be allowed to access the password file.
Access control: Another means of protecting the password file is by restricting access to the password file. Only a few users such as the system administrator must be allowed to access the password file.
3. Explain any two approaches for intrusion detection.
Ans.: To prevent intruders from getting unauthorized access to the system, intrusion prevention and intrusion detection can be used. Intrusion prevention is a process that involves detecting the signs of intrusion and attempting to stop the intrusion efforts. On the other hand, intrusion detection is a process that involves monitoring the actions occurring on the network or in the computer systems. In intrusion detection, analysis is done to detect the sign of violations of computer security policies, standard security policies or acceptable use of policies.
It is not possible to completely prevent the efforts of intruders as they constantly try to find their way into the secured system. Hence, we mainly focus on intrusion detection, as it helps collect more information about intrusions. There are generally two approaches for intrusion detection, as listed here:
 Statistical anomaly detection: In this category, the behaviour of legitimate users is evaluated over some time interval. That is, their actions are captured as statistical data and then, by applying certain rules on the collected data, their behaviour is checked to determine the legitimacy of the users. This can be achieved by two ways, namely, threshold detection and profile-based detection.
Statistical anomaly detection: In this category, the behaviour of legitimate users is evaluated over some time interval. That is, their actions are captured as statistical data and then, by applying certain rules on the collected data, their behaviour is checked to determine the legitimacy of the users. This can be achieved by two ways, namely, threshold detection and profile-based detection.
 Threshold detection: In threshold detection, thresholds are defined for all users as a group, and the total number of events that are attributed to the user are measured against these threshold values. The number of events is assumed to round up to a number that is most likely to occur, and if the event count exceeds this number, then intrusion is said to have occurred.
Threshold detection: In threshold detection, thresholds are defined for all users as a group, and the total number of events that are attributed to the user are measured against these threshold values. The number of events is assumed to round up to a number that is most likely to occur, and if the event count exceeds this number, then intrusion is said to have occurred.
 Profile-based detection: In profile-based detection, profiles for all users are created, and then matched with available statistical data to find out if any unwanted action has been performed. A user profile contains several parameters; therefore, change in a single parameter is not a sign of alert.
Profile-based detection: In profile-based detection, profiles for all users are created, and then matched with available statistical data to find out if any unwanted action has been performed. A user profile contains several parameters; therefore, change in a single parameter is not a sign of alert.
 Rule-based detection: In this category, certain rules are applied on the actions performed by the users. These rules can determine whether an action performed by any user is suspicious enough to be classified as an intrusion attempt. Rule-based detection is classified into two types, namely, anomaly detection and penetration identification.
Rule-based detection: In this category, certain rules are applied on the actions performed by the users. These rules can determine whether an action performed by any user is suspicious enough to be classified as an intrusion attempt. Rule-based detection is classified into two types, namely, anomaly detection and penetration identification.
 Anomaly-based detection: In anomaly-based detection, the usage patterns of users are collected, and certain rules are applied to check any deviation from the previous usage pasterns. The collected patterns are defined by the set of rules that includes past behaviour patterns of users, programs, privileges, time-slots, terminals, etc. The current behaviour patterns of the user are matched with the defined set of rules to check whether there is any deviation in the patterns. In this approach, a large database of rules is needed.
Anomaly-based detection: In anomaly-based detection, the usage patterns of users are collected, and certain rules are applied to check any deviation from the previous usage pasterns. The collected patterns are defined by the set of rules that includes past behaviour patterns of users, programs, privileges, time-slots, terminals, etc. The current behaviour patterns of the user are matched with the defined set of rules to check whether there is any deviation in the patterns. In this approach, a large database of rules is needed.
 Penetration identification: In penetration identification, an expert system is maintained that looks for any unwanted attempts. This system also contains rules that are used to identify the suspicious behaviour and penetrations that can exploit known weaknesses. Here, the rules are generated by interviewing experts such as system administrators and security analysts. The data collected in the interview process consist of known penetration scenarios and events that may threaten the security of the system. Thus, the rules are confined to the system and the operating system that is being used.
Penetration identification: In penetration identification, an expert system is maintained that looks for any unwanted attempts. This system also contains rules that are used to identify the suspicious behaviour and penetrations that can exploit known weaknesses. Here, the rules are generated by interviewing experts such as system administrators and security analysts. The data collected in the interview process consist of known penetration scenarios and events that may threaten the security of the system. Thus, the rules are confined to the system and the operating system that is being used.
4. Explain audit records.
Ans.: An audit record (also known as audit log) is a very important tool used in intrusion detection. Audit records are used to track the actions performed by users. If any user tries to get unauthorized access in a network, then traces of such actions can be detected in these records, so that appropriate measures can be taken. Audit records can be categorized into two types, namely, native auditrecords and detection-specific audit records.
 Native audit records: Almost all multiuser operating systems come with in-built accounting software that collects information about the actions of each user. The advantage of using this approach is that there is no need for additional collection software. However, the disadvantage is that some of the needed information may not be available in the native audit record or may be in a form that is not convenient to use.
Native audit records: Almost all multiuser operating systems come with in-built accounting software that collects information about the actions of each user. The advantage of using this approach is that there is no need for additional collection software. However, the disadvantage is that some of the needed information may not be available in the native audit record or may be in a form that is not convenient to use.
 Detection-specific audit records: These records record only specific information that is related to the detection of unauthorized access in a network. These types of records contain more focused information, but duplication of information may happen. The advantage of using this approach is that it could be made vendor-independent and can be ported onto different systems. However, the disadvantage of this approach is the extra overhead, as two accounting packages need to remain on a single machine.
Detection-specific audit records: These records record only specific information that is related to the detection of unauthorized access in a network. These types of records contain more focused information, but duplication of information may happen. The advantage of using this approach is that it could be made vendor-independent and can be ported onto different systems. However, the disadvantage of this approach is the extra overhead, as two accounting packages need to remain on a single machine.
Irrespective of the type, each audit record contains some fields, as listed here:
 Subject: This field gives the information of the user or process or terminal who has started an action.
Subject: This field gives the information of the user or process or terminal who has started an action.
 Action: This field defines the operation performed by the user (subject) on an object. For example, read/write, login, execute, print, I/O activity, etc.
Action: This field defines the operation performed by the user (subject) on an object. For example, read/write, login, execute, print, I/O activity, etc.
 Object: This field provides the information of the receiver who has received the action. For example, database record, a disk file or an application program.
Object: This field provides the information of the receiver who has received the action. For example, database record, a disk file or an application program.
 Exception-condition: This field stores the result of any exception condition, if any occurs because of the actions performed by the subject on the object.
Exception-condition: This field stores the result of any exception condition, if any occurs because of the actions performed by the subject on the object.
 Resource-usage: This field records the information regarding the usage of resources in performing an action. For example, the disk space, or CPU time used by an action, number of lines printed or displayed, or number of I/O units used.
Resource-usage: This field records the information regarding the usage of resources in performing an action. For example, the disk space, or CPU time used by an action, number of lines printed or displayed, or number of I/O units used.
 Time-stamp: This field indicates the unique date and time stamp that indicates when an action was executed.
Time-stamp: This field indicates the unique date and time stamp that indicates when an action was executed.
5. Why is distributed intrusion detection needed? Explain its architecture.
Ans.: A typical organization consists of a large collection of hosts distributed over a LAN or supported by an internetwork. One way to detect intrusion in such an organization is to use stand-alone intrusion detection systems on individual hosts. Though this type of defence is possible, it has not proved to be much effective. Thus, a better and more effective defence is required, which is achieved through coordination and cooperation among the intrusion detection systems across the network.
Figure 10.1 shows the architecture of a distributed intrusion detection system that was developed at the University of California. It consists of the following three components:
 Host agent module: This is an audit collection module that runs as a background process on the system being monitored. It is responsible for collecting information related to security on the host and reporting this to the central manager.
Host agent module: This is an audit collection module that runs as a background process on the system being monitored. It is responsible for collecting information related to security on the host and reporting this to the central manager.
 LAN manager agent module: This module works in a similar manner as that of a host agent module. However, the difference is that it examines the LAN traffic, as its name implies, rather than security-related events. It also reports the results of analysis to the central manager.
LAN manager agent module: This module works in a similar manner as that of a host agent module. However, the difference is that it examines the LAN traffic, as its name implies, rather than security-related events. It also reports the results of analysis to the central manager.
 Central manager module: This is the main module that is responsible for processing and correlating the reports received from the host agent module and LAN manager agent module in order to detect the intrusion.
Central manager module: This is the main module that is responsible for processing and correlating the reports received from the host agent module and LAN manager agent module in order to detect the intrusion.

Figure 10.1 Architecture of Distributed Intrusion Detection System
6. List some issues in the design of distributed intrusion detection systems.
Ans.: Although distributed intrusion detection systems are an effective way to prevent intrusion across the network, there are still some issues in its design. These issues are discussed as follows:
 In case different hosts in a network are not similar (that is, heterogeneous environment), the native audit collection system used by each host may differ. Further, if intrusion detection is used, different hosts may have their own format for security-related audit records. This necessitates a distributed intrusion detection system to deal with different audit formats.
In case different hosts in a network are not similar (that is, heterogeneous environment), the native audit collection system used by each host may differ. Further, if intrusion detection is used, different hosts may have their own format for security-related audit records. This necessitates a distributed intrusion detection system to deal with different audit formats.
 The intrusion detection system can be implemented using either centralized or decentralized architecture. If centralized architecture is used, the entire audit data is collected and analyzed at
a single central location. Though centralizing the data makes the task of correlating the reports easier, it results in a serious bottleneck in case of failure of the central location. On the other hand, if decentralized architecture is used, we have more than one location to collect and analyze the data. To work effectively, the coordination and exchange of information among these locations is required, which results in an extra overhead. Therefore, the choice of which architecture is to be employed is a matter of concern.
The intrusion detection system can be implemented using either centralized or decentralized architecture. If centralized architecture is used, the entire audit data is collected and analyzed at
a single central location. Though centralizing the data makes the task of correlating the reports easier, it results in a serious bottleneck in case of failure of the central location. On the other hand, if decentralized architecture is used, we have more than one location to collect and analyze the data. To work effectively, the coordination and exchange of information among these locations is required, which results in an extra overhead. Therefore, the choice of which architecture is to be employed is a matter of concern.
 As many nodes in the network are responsible for collecting and analyzing the audit data, either the raw audit data or summary data needs to be transmitted across the network. This necessitates ensuring the integrity and confidentiality of data being transmitted. Integrity refers to ensuring that the data is not altered by the intruder, and confidentiality is about maintaining the secrecy of the data.
As many nodes in the network are responsible for collecting and analyzing the audit data, either the raw audit data or summary data needs to be transmitted across the network. This necessitates ensuring the integrity and confidentiality of data being transmitted. Integrity refers to ensuring that the data is not altered by the intruder, and confidentiality is about maintaining the secrecy of the data.
7. What are honeypots?
Ans.: Honeypots are a recent innovation in intrusion detection technology. They are the traps that are designed to attract the potential intruders and, thus, track their activities. The main aim of such systems is to collect the information about the intruder's activities, deviate them from accessing the critical systems and boost them to stay on the system for more time so that the network administrator can take actions accordingly.
Honeypots are fabricated to look like real systems by putting real-looking information into them, so that they appear valuable to the potential intruders. However, legitimate users are not allowed to know about or access these systems. Thus, if anyone accesses the honeypots, he or she is a potential attacker. Honeypots are equipped with sensors and loggers to detect accesses and to track the intruder's activities.
8. How are passwords stored in a password file in the UNIX operating system? How are users authenticated?
Ans.: Earlier, in the UNIX operating system, passwords of all users were stored in plaintext in the password file, and the password file was protected by allowing it to be accessed only by the system administrator and privileged users. However, this practice may prove dangerous because any mistake in programming or any other error can make the password file vulnerable to attack. Thus, a new scheme is now used in the UNIX operating system, where the passwords are not stored in plaintext in the password file; instead, a hash of the password is computed and stored in the password file.
Each user in UNIX is allowed to choose a password of maximum eight printable characters, which are converted using 7-bit ASCII to form a 56-bit value. This 56-bit value is used as the encryption key in the encryption function, crypt(3). The crypt(3) function is based on the Data Encryption Standard (DES) algorithm. In UNIX, DES algorithm is modified with the help of 12-bit salt—a value indicating the time a password was assigned to a user. To store a password in the password file, the modified DES algorithm takes a 64-bit block consisting of 0s and encrypts it using the 56-bit encryption key. The resulting 64-bit ciphertext block serves as input for the next encryption. A total of 25 encryptions are performed, and the final obtained 64-bit ciphertext is converted to 11 printable characters. This hashed password is then stored in the password file along with the user ID and the salt.
At the time a user attempts to log on to the system, he or she presents his or her user ID and password to the system. The UNIX operating system uses the supplied user ID as index to find the corresponding entry in the password file. After finding the entry, it extracts the plaintext salt and hashed
password. The salt along with the password supplied by the user are given as input to the crypt(3) function, which then repeats the same process as described earlier to compute the hash of the password. If the newly computed value matches with the stored value in the password file, the user is authenticated; otherwise, the access is denied.
9. Discuss some password selection strategies.
Ans.: Generally, users choose passwords that are short and easy to remember. However, such passwords may be easily guessed, making it simple for intruders to hack into the corresponding user's accounts. On the other hand, if passwords given to the users are long and are randomly generated, it is not effectively possible to crack the passwords. However, such passwords are hard to remember for the users. Thus, some password-selection strategies have been introduced with the aim of building a password that cannot be easily guessed and can be easily remembered. These strategies are listed here:
 User education: This strategy is based on educating the users about the importance of using strong passwords that are difficult to guess. The users can also be provided with certain guidelines that help them in choosing hard-to-guess passwords. Though this strategy is simple, it generally fails, especially when there are a large number of users. This is because many users simply ignore the guidelines of selecting strong passwords, while others are unable to judge what a strong password is.
User education: This strategy is based on educating the users about the importance of using strong passwords that are difficult to guess. The users can also be provided with certain guidelines that help them in choosing hard-to-guess passwords. Though this strategy is simple, it generally fails, especially when there are a large number of users. This is because many users simply ignore the guidelines of selecting strong passwords, while others are unable to judge what a strong password is.
 Computer-generated passwords: In this strategy, the system randomly generates passwords for the users. Being random, these passwords may or may not be correctly pronounceable. Thus, it becomes difficult for the users to remember the passwords. The situation becomes even worse in case the password is not pronounceable because, in that case, the user does not have any choice except to write down the password somewhere, which makes it subject to be stolen by an intruder. Therefore, this technique is not so popular among the users.
Computer-generated passwords: In this strategy, the system randomly generates passwords for the users. Being random, these passwords may or may not be correctly pronounceable. Thus, it becomes difficult for the users to remember the passwords. The situation becomes even worse in case the password is not pronounceable because, in that case, the user does not have any choice except to write down the password somewhere, which makes it subject to be stolen by an intruder. Therefore, this technique is not so popular among the users.
 Reactive password checking: In this strategy, the system executes its own password cracker at regular intervals of time to identify passwords that can be guessed easily. The idea is to determine easy-to-guess passwords and to reject them, thus, improving password security. The system also notifies the corresponding users about the cancellation of their passwords. The disadvantage of this strategy is that any easy-to-guess password in the system remains vulnerable to attack as long as it is not found by the password cracker of the system.
Reactive password checking: In this strategy, the system executes its own password cracker at regular intervals of time to identify passwords that can be guessed easily. The idea is to determine easy-to-guess passwords and to reject them, thus, improving password security. The system also notifies the corresponding users about the cancellation of their passwords. The disadvantage of this strategy is that any easy-to-guess password in the system remains vulnerable to attack as long as it is not found by the password cracker of the system.
 Proactive password checker: This strategy allows users to select their passwords on their own. However, it provides sufficient guidance to the users at the time of password selection so that they can select passwords that are strong as well as easy to remember. To achieve this, the system may employ certain rules that must be followed by each user while selecting the password. For example, the system may enforce a rule that the password must be minimum eight characters long and must be the combination of lower case letters, upper case letters and numeric digits. Now, at the time of password selection, if all rules are followed by the user, the system allows the password, else rejects it.
Proactive password checker: This strategy allows users to select their passwords on their own. However, it provides sufficient guidance to the users at the time of password selection so that they can select passwords that are strong as well as easy to remember. To achieve this, the system may employ certain rules that must be followed by each user while selecting the password. For example, the system may enforce a rule that the password must be minimum eight characters long and must be the combination of lower case letters, upper case letters and numeric digits. Now, at the time of password selection, if all rules are followed by the user, the system allows the password, else rejects it.
The proactive password checker strategy is based on creating a balance between the strength of the password and user acceptability. This is essential because, if the system chooses a complex algorithm for determining whether a selected password is acceptable, then too many password rejections may occur and, as a result, the user may not find the system user-friendly. In contrast, if the system uses a simple algorithm, then it may enable a password cracker to understand the basis of password selection and, thus, help them to guess the passwords easily.
10. What do you understand by malicious software?
Ans.: Malicious software (shortened form malware) are programs that generate threats to the computer system and stored data. They could be in the form of viruses, worms, Trojan horses, logic bombs and zombie programs. All malicious programs fall under two categories: one that require a host program such as an application program or a system program in order to be executed by the operating system, and another that can be executed by the operating system independently. Some examples of malicious programs belonging to first category include viruses and logic bombs, while worms and zombie programs are examples of the second category.
11. What is a virus? Explain different types of viruses.
Ans.: Virus (stands for Vital Information Resources Under Seize) is a program or small code segment that is designed to replicate, attach to other programs and perform unsolicited and malicious actions. It enters into the computer system from external sources such as CD, pen drive or e-mail and executes when the infected program is executed. Further, as an infected computer gets in contact with an uninfected computer (for example, through computer networks), the virus may pass on to the uninfected system and destroy data.
Just as flowers are attractive to the bees that pollinate them, virus host programs are deliberately made attractive to victimize the user. They become destructive as soon as they enter a system or are programmed to lie dormant until activated by a trigger. The different types of virus are discussed as follows:
 Boot sector virus: This virus infects the master boot record of a computer system. This virus moves the boot record to another sector on the disk, or replaces it with the infected one. It then marks that sector as a bad sector on the disk. This type of virus is very difficult to detect since the boot sector is the first program that is loaded when a computer starts. In effect, the boot sector virus takes full control of the infected computer.
Boot sector virus: This virus infects the master boot record of a computer system. This virus moves the boot record to another sector on the disk, or replaces it with the infected one. It then marks that sector as a bad sector on the disk. This type of virus is very difficult to detect since the boot sector is the first program that is loaded when a computer starts. In effect, the boot sector virus takes full control of the infected computer.
 File-infecting virus: This virus infects files with the extensions .com and .exe. This type of virus usually resides inside the memory and infects most of the executable files on a system. The virus replicates by attaching a copy of itself to an uninfected executable program. It then modifies the host programs and, subsequently, when the program is executed, it executes along with it. File-infecting virus can only gain control of the computer if the user or the operating system executes a file infected with the virus.
File-infecting virus: This virus infects files with the extensions .com and .exe. This type of virus usually resides inside the memory and infects most of the executable files on a system. The virus replicates by attaching a copy of itself to an uninfected executable program. It then modifies the host programs and, subsequently, when the program is executed, it executes along with it. File-infecting virus can only gain control of the computer if the user or the operating system executes a file infected with the virus.
 Polymorphic virus: This virus changes its code as it propagates from one file to another. Therefore, each copy of virus appears different from others; however, they are functionally similar. This makes the polymorphic virus difficult to detect, like the stealth virus. The variation in copies is achieved by placing superfluous instructions in the virus code or by interchanging the order of instructions that are not dependent. Another more effective means to achieve variation is by using encryption. A part of the virus, called the mutation engine, generates a random key that is used to encrypt the rest of the virus. The random key is kept stored with the virus, while the mutation engine changes by itself. At the time the infected program is executed, the stored key is used by the virus to decrypt itself. Each time the virus replicates, the random key changes.
Polymorphic virus: This virus changes its code as it propagates from one file to another. Therefore, each copy of virus appears different from others; however, they are functionally similar. This makes the polymorphic virus difficult to detect, like the stealth virus. The variation in copies is achieved by placing superfluous instructions in the virus code or by interchanging the order of instructions that are not dependent. Another more effective means to achieve variation is by using encryption. A part of the virus, called the mutation engine, generates a random key that is used to encrypt the rest of the virus. The random key is kept stored with the virus, while the mutation engine changes by itself. At the time the infected program is executed, the stored key is used by the virus to decrypt itself. Each time the virus replicates, the random key changes.
 Stealth virus: This virus attempts to conceal its presence from the user. It makes use of compression such that the length of infected program is exactly same as that of the uninfected version. For example, it may keep intercept logic in some I/O routines so that when some other program requests for information from the suspicious portions of the disk using these routines, it will present the original uninfected version to the program. The Stoned Monkey virus is an example
of stealth virus. This virus uses ‘read stealth’ capability, and if a user executes a disk-editing or antivirus program to examine the main boot record, the user would not find any evidence of infection.
Stealth virus: This virus attempts to conceal its presence from the user. It makes use of compression such that the length of infected program is exactly same as that of the uninfected version. For example, it may keep intercept logic in some I/O routines so that when some other program requests for information from the suspicious portions of the disk using these routines, it will present the original uninfected version to the program. The Stoned Monkey virus is an example
of stealth virus. This virus uses ‘read stealth’ capability, and if a user executes a disk-editing or antivirus program to examine the main boot record, the user would not find any evidence of infection.
 Multipartite virus: This virus infects both boot sectors and executable files, and uses both mechanisms to spread. It is the worst virus of all because it can combine some or all of the stealth techniques along with polymorphism to prevent detection. For example, if a user runs an application infected with a multipartite virus, the virus activates and infects the hard disk's master boot record. Moreover, the next time the computer starts; the virus gets activated again and starts infecting every program that the user runs. One-half virus is an example of a multipartite virus, which exhibits both stealth and polymorphic behaviour.
Multipartite virus: This virus infects both boot sectors and executable files, and uses both mechanisms to spread. It is the worst virus of all because it can combine some or all of the stealth techniques along with polymorphism to prevent detection. For example, if a user runs an application infected with a multipartite virus, the virus activates and infects the hard disk's master boot record. Moreover, the next time the computer starts; the virus gets activated again and starts infecting every program that the user runs. One-half virus is an example of a multipartite virus, which exhibits both stealth and polymorphic behaviour.
12. What are the typical phases of operation of a virus?
Ans.: Virus is a destructive program that attaches to other programs, replicates itself and performs malicious actions when the host program is executed. The whole operation of a virus involves the following four phases.
 Dormant phase: This is the initial phase in the lifetime of a virus. During this phase, the virus remains idle; however, later, it is activated due to occurrence of some events including the date, time, capacity of disk beyond limit or the presence of some other program or file. It may be noted that this phase exists only in case of some viruses and not all.
Dormant phase: This is the initial phase in the lifetime of a virus. During this phase, the virus remains idle; however, later, it is activated due to occurrence of some events including the date, time, capacity of disk beyond limit or the presence of some other program or file. It may be noted that this phase exists only in case of some viruses and not all.
 Propagation phase: During this phase, the virus replicates itself and infects other programs as well as some disk areas by putting its identical copies (referred to as clones) into them. All the infected programs now contain the same virus, which has already entered into the propagation phase.
Propagation phase: During this phase, the virus replicates itself and infects other programs as well as some disk areas by putting its identical copies (referred to as clones) into them. All the infected programs now contain the same virus, which has already entered into the propagation phase.
 Triggering phase: In this phase, the virus is activated to enter the execution phase, so that it can perform its intended action. The activation of the virus may occur due to the events as specified in dormant phase. In addition, it also takes into account the number of times a single copy of virus replicates itself.
Triggering phase: In this phase, the virus is activated to enter the execution phase, so that it can perform its intended action. The activation of the virus may occur due to the events as specified in dormant phase. In addition, it also takes into account the number of times a single copy of virus replicates itself.
 Execution phase: This is the last phase of the virus's operation where it performs the function for which it was designed. The functions performed by viruses range from simple harmless functions such as displaying a message on the screen to serious malicious functions such as destroying programs and data files.
Execution phase: This is the last phase of the virus's operation where it performs the function for which it was designed. The functions performed by viruses range from simple harmless functions such as displaying a message on the screen to serious malicious functions such as destroying programs and data files.
13. Write a short note on the following:
(a) Worms
(b) Trojan horses
(c) Logic bomb
(d) Spyware
Ans.: (a) Worms: Worms are programs constructed to infiltrate into legitimate data processing programs and alter or destroy the data. They often use network connections to spread from one computer system to another; thus, worms attack systems that are linked through communication lines. Once active within a system, worms behave like a virus and perform a number of disruptive actions. To reproduce themselves, worms make use of network medium such as: network mail facility, in which a worm can mail a copy of itself to other systems, remote execution capability, in which a worm can execute a copy of itself on another system and remote log in capability, whereby a worm can log into a remote system as a user and then use commands to copy itself from one system to another.
Both worms and viruses tend to fill computer memory with useless data thereby preventing users from using memory space for the intended applications or programs. In addition, they can destroy or modify data and programs to produce erroneous results, as well as halt the operation of a computer
system or network. Similar to a virus, the operation of a network worm also involves dormant, propagation, triggering and execution phases.
(b)Trojan horse: A Trojan horse is a malicious program that appears to be legal and useful but concurrently does something unexpected, such as destroying existing programs and files. It does not replicate itself in the computer system and, hence, it is not a virus. However, it usually opens the way for other malicious programs such as viruses to enter into the computer system. In addition, it may also allow unauthorized users to access the information stored in the computer.
Trojan horses spread when users are convinced to open or download a program because they think it has come from a legitimate source. They can also be included in software that is freely downloadable. They are usually subtler, especially in the cases where they are used for espionage. They can be programmed to self-destruct, without leaving any evidence other than the damage they have caused. The most famous Trojan horse is a program called back orifice, which is an unsubtle play of words on Microsoft's Back Office suite of programs for NT server. This program allows anybody to have the complete control over the computer or server it occupies.
(c)Logic bomb: A logic bomb is a program or portion of a program that lies dormant until a specific part of program logic is activated. The most common activator for a logic bomb is date. The logic bomb periodically checks the computer system date and does nothing until a pre-programmed date and time is reached. It could also be programmed to wait for a certain message from the programmer. When logic bomb sees the message, it gets activated and executes the code. A logic bomb can also be programmed to activate on a wide variety of other variables such as when a database grows past a certain size or a user's home directory is deleted. For example, the well-known logic bomb is a Michelangelo, which has a trigger set for Michelangelo's birthday. On the given birth date, it causes system crash or data loss or other unexpected interactions with existing code.
(d)Spyware: Spyware are the small programs that install themselves on computers to gather data secretly about the computer user without his or her consent and report the collected data to interested users or parties. The information gathered by the spyware may include e-mail addresses and passwords, net surfing activities, credit card information, etc. Spyware often gets automatically installed on your computer when you download a program from the Internet or click any option from pop-up windows in the browser.
14. What is an antivirus? What are its approaches?
Ans.: An antivirus is an application software that is used for providing protection against malicious software. It is a software utility that (upon installing on a computer) detects viruses and, if found, tries to remove them. The built-in scanner of antivirus software scans all the files on the computer's hard disk to look for particular types of code within programs. Most antivirus programs include an auto-update feature that enables the program to download profiles of new viruses so that it can check for the new viruses as soon as they are discovered. The most popular available antivirus software includes Norton antivirus, McAfee antivirus and Quick Heal antivirus.
Antivirus Approaches
A simple and ideal approach against threat of viruses is to prevent them from entering into the system. Practically, it is not possible to achieve total prevention; however, the frequency of successful virus attacks can be reduced. Thus, an alternative approach is used that is based on the detection, identification and removal of viruses from the infected programs.
 Detection: In case the system has been infected by viruses, the first step is to identify that the infection has occurred and where it has occurred, that is, the location of the virus.
Detection: In case the system has been infected by viruses, the first step is to identify that the infection has occurred and where it has occurred, that is, the location of the virus.
 Identification: After the infection has been detected and the virus located, the next step is to determine the specific type of virus that has infected the file.
Identification: After the infection has been detected and the virus located, the next step is to determine the specific type of virus that has infected the file.
 Removal: After identifying the specific virus in a file, the final step is to remove it completely from the infected file and to bring the file back to its original state. The virus must be removed from all the systems in the network in order to prevent it from spreading further.
Removal: After identifying the specific virus in a file, the final step is to remove it completely from the infected file and to bring the file back to its original state. The virus must be removed from all the systems in the network in order to prevent it from spreading further.
15. List and brief the different generations of antivirus software.
Ans.: Earlier, viruses were simple code fragments; thus, antivirus software packages used for those viruses were also simpler. However, with the evolution in virus as well as antivirus technology, the attackers have generated more complex viruses that are not easily detectable. To protect against such viruses, antivirus software have also grown complex. The growth of antivirus software has been divided into four generations which are as follows:
 First generation: The antivirus software of this generation used simple scanners that rely on virus signatures to detect viruses. It detects viruses that have basically the same structure and the same bit pattern in all copies. However, these types of scanners can detect only the known viruses. Another type of scanner used in the first generation maintains a record of the program length, and monitors the change in length for detecting the viruses.
First generation: The antivirus software of this generation used simple scanners that rely on virus signatures to detect viruses. It detects viruses that have basically the same structure and the same bit pattern in all copies. However, these types of scanners can detect only the known viruses. Another type of scanner used in the first generation maintains a record of the program length, and monitors the change in length for detecting the viruses.
 Second generation: The antivirus software of this generation used heuristic scanners that rely on some heuristic rules to detect virus infections. One approach to detect virus infection is to scan the files and look for code fragments that are usually related to viruses. For example, in case of a polymorphic virus, the scanner may determine the starting of the encryption loop and then find the encryption key. Once the scanner has found the key, it cleans the virus infection from the infected program by decrypting the code fragment with the key and then returns the virus-free program back to service.
Second generation: The antivirus software of this generation used heuristic scanners that rely on some heuristic rules to detect virus infections. One approach to detect virus infection is to scan the files and look for code fragments that are usually related to viruses. For example, in case of a polymorphic virus, the scanner may determine the starting of the encryption loop and then find the encryption key. Once the scanner has found the key, it cleans the virus infection from the infected program by decrypting the code fragment with the key and then returns the virus-free program back to service.
Another approach for detecting virus infection is integrity checking. In this approach, a checksum is added at the end of each program. If any program gets infected by a virus, however, with no change in the checksum, the change in program can be detected by performing an integrity check. On the other hand, if a virus is so complex that it changes the checksum in addition to the program, then an encrypted hash function can be used to deal with the virus. By storing the encryption key at a different location from that of the program, we can prevent a virus from generating a new hash code and then encrypting it. Moreover, the use of the hash function instead of checksum prevents the virus from adapting the program to generate the same hash code as previously.
 Third generation: The antivirus software of this generation are the memory-resident programs that do not take into account the structure of viruses or heuristic rules to identify them. Rather, they scan the program to look for a small set of actions that indicate the infection and then deal with the viruses. An advantage is that it is not required to maintain any signatures or rules for a wide range of viruses in order to detect an infection.
Third generation: The antivirus software of this generation are the memory-resident programs that do not take into account the structure of viruses or heuristic rules to identify them. Rather, they scan the program to look for a small set of actions that indicate the infection and then deal with the viruses. An advantage is that it is not required to maintain any signatures or rules for a wide range of viruses in order to detect an infection.
 Fourth generation: The antivirus software of this generation are the packages that use scanning and activity trapping components in conjunction. These packages also comprise the access control capability, which restricts the viruses from entering into the system and updating the files for spreading the infection. All these features collectively strengthen the ability of the antivirus software.
Fourth generation: The antivirus software of this generation are the packages that use scanning and activity trapping components in conjunction. These packages also comprise the access control capability, which restricts the viruses from entering into the system and updating the files for spreading the infection. All these features collectively strengthen the ability of the antivirus software.
16. What is digital immune system? Explain how it works.
Ans.: With the increased use of Internet-based capabilities such as integrated mail systems (Lotus Notes and Microsoft Outlook) and mobile-program systems (Java and ActiveX), the threat of Internet-based virus propagation has also risen. Therefore, IBM has developed the digital immune system in response to these Internet-based virus threats. The goal of this system is to offer a very fast response time so that the viruses can be removed instantly as they enter into the system. Whenever a new virus is introduced into an organization, it is automatically captured by the digital immune system, which then examines it, adds detection and shielding for it and removes it from the system. The immune system also passes the information related to that virus to the other systems that are running the IBM antivirus, so that those systems can detect this virus before it begins to run.
The operation of the digital immune system involves the following steps (see Figure 10.2):
1. The monitoring program installed on each client machine in the organization detects the presence of a virus using various heuristic rules based on system behaviour, virus signatures or unexpected changes in the programs. In case any program on a client machine is found infected by a virus, the monitoring program sends a copy of that program to the administrative machine within the organization.
2. The administrative machine encrypts the copy of infected program received from monitoring program and forwards it to a central virus analysis machine.
3. The virus analysis machine is responsible for analyzing the infected program to detect new viruses. It creates an environment in which the infected program can be executed and analyzed. During execution, the structure and behaviour of the virus is analyzed and, based on this analysis, a virus signature is extracted. Now, the virus analysis machine examines the infected program for the extracted signature and produces a prescription for identifying and removing that virus.
4. The prescription produced by the virus analysis machine is then sent back to the administrative machine from where the infected program came.
5. The administrative machine sends the prescription to the infected client machine as well as to other client machines in the organization.
6. The prescription is also forwarded to all the subscribers and the individual user who are outside the organization network, so that they too can protect their systems from the new virus.

Figure 10.2 Operation of Digital Immune System
17. Discuss on behaviour-blocking software?
Ans.: Behaviour-blocking software is an approach to countering viruses that, unlike other approaches, is integrated with the operating system of a host computer. To detect a program for viral infections, it monitors the behaviour of a program in real time to determine any malicious actions. In case any attempt for a malicious action is detected, the behaviour-blocking software blocks the malicious action before it can affect the system. Certain malicious actions for which a program is analyzed are as follows:
 Attempts for viewing, opening, deleting and modifying files
Attempts for viewing, opening, deleting and modifying files
 Attempts for formatting disk drives
Attempts for formatting disk drives
 Starting network communications
Starting network communications
 Changes in important system settings
Changes in important system settings
 Changes in the logic of executable files.
Changes in the logic of executable files.
Behaviour-blocking software can block the malicious behaviours of a program in real time and/or terminate the entire program if it detects that the program may cause threat as it executes. The advantage of this software over other antivirus approaches is that it is able to detect and then block the malicious actions even if the instructions of a malicious code are modified or rearranged in order to evade detection. However, the disadvantage is that the as behaviours of a malicious code can be identified only after actually executing it on the machine, the malicious code may cause severe destruction to the system before its behaviours have been detected and blocked by the behaviour-blocking software.
18. What do you mean by firewall? Describe its characteristics.
Ans.: The progressive use of the Internet in organizations has opened up possibilities for the outside world to interact with internal networks, creating a great threat to the organization. Usually, organizations have huge amount of confidential data, leaking of which may prove to be a serious setback. Moreover, it is also necessary to protect the internal network against malicious programs such as virus and worms. Therefore, some mechanism is needed to ensure that the valuable data within the organization remains inside, as well as that outside attackers cannot break the security of the internal network.
A firewall is a mechanism that protects and isolates the internal network from the outside world. Simply put, a firewall prevents certain outside connections from entering into the network. It traps inbound or outbound packets, analyses them, and then permits access or discards them. Basically, a firewall is a router or a group of routers and computers that filter the traffic and implement access control between an un-trusted network (Internet) and the more trusted internal networks. Depending on the criteria used for filtering traffic, there are three common types of firewalls: packet filters (or packet-filtering router), application-level gateways and circuit-level gateways.
The characteristics of a firewall are as follows:
 A firewall specifies a single choke point by consolidating all the security-related capabilities into a single system or a set of systems. This results in simplified security management.
A firewall specifies a single choke point by consolidating all the security-related capabilities into a single system or a set of systems. This results in simplified security management.
 The choke point stops vulnerable services from entering or exiting through the network, prevents the intruders from accessing the protected network and protects against attacks such as IP spoofing.
The choke point stops vulnerable services from entering or exiting through the network, prevents the intruders from accessing the protected network and protects against attacks such as IP spoofing.
 It provides support for performing various Internet functions such as mapping a local address to an Internet address or maintaining logs for recording the usage of Internet, etc.
It provides support for performing various Internet functions such as mapping a local address to an Internet address or maintaining logs for recording the usage of Internet, etc.
 Virtual private networks can be implemented using firewalls.
Virtual private networks can be implemented using firewalls.
 A firewall specifies a single location from where all security-related events can be monitored and analyzed. Alarms and audits can also be used with firewall systems to protect against unauthorized events.
A firewall specifies a single location from where all security-related events can be monitored and analyzed. Alarms and audits can also be used with firewall systems to protect against unauthorized events.
19. List some limitations of firewalls.
Ans.: Though the firewall is an effective means of providing security to an organization, it has certain limitations, which are as follows:
 A firewall provides effective security to the internal network if it is configured as the only entry-exit point in the organization. However, if there are multiple entry-exit points in the organization and firewall is implemented at just one of them, then the incoming or outgoing traffic may bypass the firewall. This makes the internal network susceptible to attack through the points where the firewall has not been implemented.
A firewall provides effective security to the internal network if it is configured as the only entry-exit point in the organization. However, if there are multiple entry-exit points in the organization and firewall is implemented at just one of them, then the incoming or outgoing traffic may bypass the firewall. This makes the internal network susceptible to attack through the points where the firewall has not been implemented.
 A firewall is designed to protect against outside attacks. However, it does not have any mechanism to protect against internal threats such as an employee of a company who unknowingly helps an external attacker.
A firewall is designed to protect against outside attacks. However, it does not have any mechanism to protect against internal threats such as an employee of a company who unknowingly helps an external attacker.
 The firewall does not provide protection against any virus-infected program or files being transferred through the internal network. This is because it is almost impossible to scan all the files entering in the network for viruses. To protect the internal network against virus threats, a separate virus detection and removal strategy should be used.
The firewall does not provide protection against any virus-infected program or files being transferred through the internal network. This is because it is almost impossible to scan all the files entering in the network for viruses. To protect the internal network against virus threats, a separate virus detection and removal strategy should be used.
20. Discuss the packet-filtering router firewall.
Ans.: A packet-filtering router, also known as screening router or screening filter, is the one of the oldest firewall technologies that operates at the network layer. It examines the incoming and outgoing packets by applying a fixed set of rules on them and, thus, determines whether to forward the packets or to reject them. The rules used for filtering the packets are defined based on the following information contained in a network (IP) packet.
 The IP address of the system from where the packet has come
The IP address of the system from where the packet has come
 The IP address of the system for which the packet is destined
The IP address of the system for which the packet is destined
 The transport layer protocol used such as TCP or UDP
The transport layer protocol used such as TCP or UDP
 Transport-level address (that is, port number) of source and destination, which identifies the application such as Telnet or SNMP
Transport-level address (that is, port number) of source and destination, which identifies the application such as Telnet or SNMP
 The interface of the router where the packet came from or is destined to.
The interface of the router where the packet came from or is destined to.
The filtering rules specify which packets are allowed to pass through and in which direction they should flow, that is, from external to internal network or vice versa. Each rule has a specified action associated with it, either to allow or to deny a packet. Thus, there are two sets of filtering rules: allow, which permits the traffic, and deny, which discards the traffic. While examining a packet, if a match is found with any of the allow set of rules, then the packet is forwarded to the desired destination. On the other hand, if a match is found with any of the deny set of rules, the packet is discarded. In case no match is found, the default action is taken. The default policy can be either to forward or discard the packet. The former default policy provides more ease of use to the end users; however, it offers a reduced level of security. In contrast, the latter default policy is more conservative; however, it provides more security. Therefore, generally, the implementation of a firewall is initiated with default discard policy and, later, packet filtering is enforced by applying the rules one by one.
Advantages
Some advantages of packet filters are as follows:
 They are simple, since a single rule is enough to indicate whether to allow or deny the packet.
They are simple, since a single rule is enough to indicate whether to allow or deny the packet.
 They are transparent to the users; the users need not know the existence of packet filters.
They are transparent to the users; the users need not know the existence of packet filters.
 They operate at a fast speed as compared to other techniques.
They operate at a fast speed as compared to other techniques.
 The client computers need not be configured specially while implementing packet-filtering firewalls.
The client computers need not be configured specially while implementing packet-filtering firewalls.
 They protect the IP addresses of internal hosts from the outside network.
They protect the IP addresses of internal hosts from the outside network.
Disadvantages
Some disadvantages of packet filters are as follows:
 They are unable to inspect the application layer data in the packets and thus, cannot restrict access to ftp services.
They are unable to inspect the application layer data in the packets and thus, cannot restrict access to ftp services.
 It is a difficult task to set up the packet-filtering rules correctly.
It is a difficult task to set up the packet-filtering rules correctly.
 They lack support for authentication and have no alert mechanisms.
They lack support for authentication and have no alert mechanisms.
 Being stateless in nature, they are not well suited to application layer protocols.
Being stateless in nature, they are not well suited to application layer protocols.
21. What kind of attacks is possible on packet-filtering firewalls. Suggest appropriate countermeasures.
Ans.: Though packet-filtering firewalls operate at a fast speed and do not require users to be aware of packet filters, they are still prone to some attacks, which are as follows:
 IP address spoofing: In this attack, an intruder external to the organization's network sends a packet towards the network. The IP address of this packet is the same as that of one of the hosts in the network. The attacker thinks that he or she can penetrate into the internal network by spoofing IP address and, therefore, can attack on the systems easily. To prevent such attacks, packet-filtering firewalls should discard all the packets coming to the organization's network, which contains the IP address of any internal host.
IP address spoofing: In this attack, an intruder external to the organization's network sends a packet towards the network. The IP address of this packet is the same as that of one of the hosts in the network. The attacker thinks that he or she can penetrate into the internal network by spoofing IP address and, therefore, can attack on the systems easily. To prevent such attacks, packet-filtering firewalls should discard all the packets coming to the organization's network, which contains the IP address of any internal host.
 Source routing attack: In this attack, an intruder specifies the pre-defined route that a packet should take to reach its destination by selecting a particular option in the IP packet header. By choosing such an option, the intruder hopes that the packet-filtering firewall will bypass the security measures of checking the source routing information. The countermeasure for this attack is that packet-filtering firewalls should discard all the packets that are using this option.
Source routing attack: In this attack, an intruder specifies the pre-defined route that a packet should take to reach its destination by selecting a particular option in the IP packet header. By choosing such an option, the intruder hopes that the packet-filtering firewall will bypass the security measures of checking the source routing information. The countermeasure for this attack is that packet-filtering firewalls should discard all the packets that are using this option.
 Tiny fragment attack: In this attack, an intruder takes advantage of the IP packet fragmentation option and intentionally divides the original IP packet into small fragments. This is done to force the TCP header information to go into a separate packet fragment. The intruder hopes that the filtering rules that are based on the TCP header information can be circumvented this way, and that the packet-filtering firewall can be fooled such that it will examine only the first fragment of the packet and the rest will bypass through it without any checks. This attack can be prevented by discarding all the fragmented packets that are using TCP as the upper-layer protocol type.
Tiny fragment attack: In this attack, an intruder takes advantage of the IP packet fragmentation option and intentionally divides the original IP packet into small fragments. This is done to force the TCP header information to go into a separate packet fragment. The intruder hopes that the filtering rules that are based on the TCP header information can be circumvented this way, and that the packet-filtering firewall can be fooled such that it will examine only the first fragment of the packet and the rest will bypass through it without any checks. This attack can be prevented by discarding all the fragmented packets that are using TCP as the upper-layer protocol type.
22. Write a short note on application-level gateways.
Ans.: An application-level gateway operates at the application layer of the OSI model. It is also termed as a proxy server (or simply called proxy), which handles the flow of application-level traffic. The operation of application-level gateways is as follows:
1. A user contacts the application gateway with the help of a TCP/IP application such as Telnet, FTP or HTTP.
2. In response, the application gateway asks the user for the name, IP address and other information about the remote host that is to be accessed. It also asks the user to present its user ID and password to access the gateway.
3. The user supplies a valid user ID, password and other desired information to the gateway.
4. After verifying the user, the application gateway contacts the application running on the remote host on behalf of the user. The TCP segments comprising the application data are exchanged between the two end points.
5. Now, the application gateway serves as a proxy of the original user and delivers application data in both directions, from remote host to the user and vice versa.
Advantages
Application-level gateways are considered the most secure type of firewalls since they provide a number of advantages, which are as follows:
 The entire communication between the internal and external network happens only through the application gateways. This protects the internal IP addresses from the external network.
The entire communication between the internal and external network happens only through the application gateways. This protects the internal IP addresses from the external network.
 The use of application gateways provides transparency between the users and the external network.
The use of application gateways provides transparency between the users and the external network.
 They understand and implement high-level protocols such as HTTP and FTP.
They understand and implement high-level protocols such as HTTP and FTP.
 They support functions such as user authentication, caching, auditing and logging.
They support functions such as user authentication, caching, auditing and logging.
 They can process and manipulate the packet data.
They can process and manipulate the packet data.
 Strong user authentication can be enforced with application gateways.
Strong user authentication can be enforced with application gateways.
 They can disallow access to certain network services and allow others at the same time.
They can disallow access to certain network services and allow others at the same time.
Disadvantages
Some disadvantages of application-level gateways are as follows:
 Each new network service requires a number of proxy services to be added. Thus, application-level gateways are not scalable.
Each new network service requires a number of proxy services to be added. Thus, application-level gateways are not scalable.
 The addition of proxy services causes client applications to be modified.
The addition of proxy services causes client applications to be modified.
 Application gateways operate at a slower speed and, as a result, network performance degrades.
Application gateways operate at a slower speed and, as a result, network performance degrades.
 As they rely on the support provided by the underlying operating system, they are vulnerable to the bugs in the system.
As they rely on the support provided by the underlying operating system, they are vulnerable to the bugs in the system.
23. When the system administrator trusts the internal users, what type of firewall is to be used? What are its advantages and disadvantages?
Ans.: For a situation where the system administrator trusts the internal users, circuit-level gateways are the best suited. Circuit-level firewalls operate in a similar manner as that of packet-filtering firewalls, except that they operate at the session and transport layers of the OSI model. Whenever a session is to be established between a host in the internal network and a host outside the internal network, two TCP connections are to be established, one between the TCP user in the internal network and the circuit-level gateway, and another between the circuit-level gateway and the TCP user in the external network. After both the connections have been established, the circuit-level gateway forwards the packet from one connection to another without inspecting their contents. This is because, in circuit-level gateways, the session is validated before opening the connections. Thus, there is no need to examine the packet contents once the session has been established.
Circuit-level gateways maintain a virtual table to store session-related information of all the valid connections. This information includes the session date, a unique session identifier, connection state, IP addresses of source and destination, the sequencing information and the physical network interface through which the packet has come and has to go. Rather than allowing all packets that meet the rule set requirements to pass, it allows only those packets that are part of a valid, established connection.
Advantages
Some advantages of circuit-level gateways are as follows:
 They operate at a faster speed as compared to application-level gateways.
They operate at a faster speed as compared to application-level gateways.
 They offer more security than packet filters.
They offer more security than packet filters.
 They are not subject to IP address spoofing attacks.
They are not subject to IP address spoofing attacks.
 They perform network address translation (NAT) by changing source node IP address to its own and, thus, protecting internal host IP addresses from the external network.
They perform network address translation (NAT) by changing source node IP address to its own and, thus, protecting internal host IP addresses from the external network.
Disadvantages
Some disadvantages of circuit-level gateways are as follows:
 They are unable to perform security checks on higher-level protocols.
They are unable to perform security checks on higher-level protocols.
 They can restrict access only to TCP protocol subsets.
They can restrict access only to TCP protocol subsets.
 They have only a confined audit event generation capability.
They have only a confined audit event generation capability.
24. What is the role of bastion host?
Ans.: A bastion host is a system in an organization's internal network that acts as a vital point in the security of the network. This system is distinguished from other systems by the firewall administrator and serves as a platform for an application-level or circuit-level gateway. The hardware platform of the bastion host executes a secured version of the operating system and, therefore, behaves like a trusted system. Moreover, only limited proxy applications that are considered necessary by the network administrator, such as Telnet, DNS and SMTP, are installed on the bastion host. It requires additional authentication if any user wants access to these proxy services, and each proxy service needs its own authentication. Thus, the role of bastion host is to enhance the security of the network, so that it becomes more difficult for intruders to gain access to the internal network.
25. Describe the common types of firewall configurations.
Ans.: Firewalls may be implemented as a single system, such as a single packet filter or a single application gateway, or it may be implemented as a combination of packet filters and application gateways. There are three possible firewall configurations, which are as follows:
 Screened host firewall, single-homed bastion: In this firewall configuration, a packet filter and an application gateway (bastion host) are used in combination. The packet filter checks the traffic from the Internet to the internal corporate network and from the internal corporate network to the Internet, based on the specific rule. It allows packets from outside the network to enter the internal network if it is destined for the application gateway. Similarly, it allows packets from the internal network to move to the outside network only if the packet has originated from the application gateway. The application gateway is responsible for performing authentication and proxy functions.
Screened host firewall, single-homed bastion: In this firewall configuration, a packet filter and an application gateway (bastion host) are used in combination. The packet filter checks the traffic from the Internet to the internal corporate network and from the internal corporate network to the Internet, based on the specific rule. It allows packets from outside the network to enter the internal network if it is destined for the application gateway. Similarly, it allows packets from the internal network to move to the outside network only if the packet has originated from the application gateway. The application gateway is responsible for performing authentication and proxy functions.
This firewall configuration enhances the security of the network by implementing both packet-level and application-level filtering. The intruder now has to penetrate two separate firewalls in order to breach the security of the network. Moreover, it allows the network administrator more freedom in defining security policy. However, the demerit of this configuration is that internal hosts are connected to the packet filter as well as the application gateway. Therefore, if the security of the packet filter router is compromised, then an intruder can gain access to the whole internal network.
 Screened host firewall, dual-homed bastion: In this firewall configuration, the internal hosts of the network are not directly connected to the packet filter. Rather, the packet filter is directly connected only to the application gateway, which has separate connections with the internal hosts. This arrangement overcomes the problem of a screened host, single-homed bastion configuration. Thus, even if the packet filter is successfully attacked by an intruder, he or she gains access only to the application gateway and not to the whole network.
Screened host firewall, dual-homed bastion: In this firewall configuration, the internal hosts of the network are not directly connected to the packet filter. Rather, the packet filter is directly connected only to the application gateway, which has separate connections with the internal hosts. This arrangement overcomes the problem of a screened host, single-homed bastion configuration. Thus, even if the packet filter is successfully attacked by an intruder, he or she gains access only to the application gateway and not to the whole network.
 Screened subnet firewall: In this firewall configuration, two packet filters and one application gateway are used. One of the packet filters connects the outside network with the application gateway and other packet filter connects the internal hosts with the application gateway. It is the most secured type of configuration as an intruder has to attack three levels before gaining an access to the internal network.
Screened subnet firewall: In this firewall configuration, two packet filters and one application gateway are used. One of the packet filters connects the outside network with the application gateway and other packet filter connects the internal hosts with the application gateway. It is the most secured type of configuration as an intruder has to attack three levels before gaining an access to the internal network.
26. What do you understand by a trusted system?
Ans.: A computer and operating system that can be relied upon to a determined level to implement a given security policy is referred to as a trusted system. In other words, a trusted system is defined as the one system whose failure may cause a specified security policy to be compromised. Trusted systems are of prime importance in areas where it is required to protect the system resources or the information on the basis of levels of security defined; that is, where multilevel security is needed. For example, in military, the information is classified into various levels such as unclassified (U), confidential (C), secret (S) and top secret (TS), and each user is allowed to access only certain levels of information. In addition to military, the trusted systems are also being prominently used nowadays in banking and financial areas.
Central to the trusted systems is the reference monitor, which is an entity residing in the operating system of a computer and entrusted the responsibility of making all the access-control-related decisions on the basis of the defined security levels. The reference monitor is expected to be tamperproof, always invoked and subject to independent testing.
Multiple-choice Questions
1. Which of the following is a type of intruder?
(a) Masquerader
(b) Misfeasor
(c) Clandestine user
(d) All of these
2. The __________ strategy aware all the users about the importance of non-guessable or strong passwords.
(a) User education
(b) Reactive password checking
(c) Proactive password checker
(d) None of these
3. A virus is a computer __________.
(a) File
(b) Network
(c) Program
(d) Database
4. A __________ replicates itself by creating its own copies, in order to bring the network to a halt.
(a) Worm
(b) Virus
(c) Trojan horse
(d) Logic bomb
5. The __________ generation of antivirus software uses heuristic scanners.
(a) First
(b) Second
(c) Third
(d) Fourth
6. The digital immune system was developed by __________.
(a) HCL
(b) IEEE
(c) ANSI
(d) IBM
7. The firewall should be situated __________.
(a) Outside a network
(b) Inside a network
(c) Between a network and the outside world
(d) None of these
8. __________ firewall is mostly used in small businesses.
(a) Packet-filtering
(b) Circuit-level gateway
(c) Application-level gateway
(d) None of these
9. Circuit-level gateways are __________ as compared to packet filters.
(a) Less secure
(b) More secure
(c) Slower
(d) None of these
10. The trap set to attract the potential intruders is known as __________.
(a) Honeypot
(b) Trapdoor
(c) Proxy
(d) All of these
Answers
1. (d)
2. (a)
3. (c)
4.(a)
5.(b)
6.(d)
7.(c)
8.(a)
9.(b)
10.(a)
A
Advanced Encryption Standard (AES), 56–58
AES. See Advanced Encryption Standard (AES)
AH. See Authentication Header (AH)
alert protocol, 161
algebraic structure, 19
antivirussoftware, 176
application-level gateways, 180–181
arbitrated digital signature, 114–115
asymmetric-key cryptography, 76
characteristics of, 76
asymmetric-key encipherment, 11
audit records, 169
Authentication Header (AH), 151–152
avalanche effect, 51
B
bastion host, 182
behavior-blocking software, 178
birthday bound, 95
birthday paradox, 95
bit-oriented cipher, 33
boot sector virus, 173
C
Caesar cipher, 26
certificate renewable, 137–138
Certificate Revocation List (CRL), 137
change cipher spec protocol, 161
Chinese Remainder Theorem (CRT), 69–70
chosen-ciphertext attack, 77–78
Cipher Block Chaining (CBC) mode, 62
Cipher Feedback (CFB)mode, 62–63
cipher key, 45
ciphers, 10
ciphertext, 9
classical encryption techniques, 25
different categories of, 25
columnar transposition cipher, 32
common modulus attack, 78
completeness effect, 51
compression function, 96
congruence, 17
conventional encryption model, 24–25
issuesin, 25
co-prime, 65
CRT. See Chinese Remainder Theorem (CRT)
cryptography, 9
D
Data Encryption Standard (DES), 45
strength of, 49
decryption, 10
DES. See Data Encryption Standard (DES)
detection-specific audit records, 169
differential cryptanalysis, 50
Diffie-Hellman key exchange algorithm, 81–82
advantages of, 82
limitations of, 82
diffusion, 35
digital immune system, 176–177
attacks on, 113
process of, 112
properties and requirements of, 113
Digital Signature Standard (DSS), 117–119
direct digital signature, 114
directory authentication service, 138
discrete logarithmic problems, 70–71
distributed intrusion detection, 170
architecture of, 170
distributed intrusion detection systems, 170–171
DSS. See Digital Signature Standard (DSS)
E
ECC. See elliptic curve cryptosystem (ECC)
Electronic Code Book (ECB) mode, 61
ElGamal algorithm, 85
attacks on, 85
encryption and decryption process, 83–84
ElGamal encryption system, 83–84
elliptic curve cryptosystem (ECC), 86
elliptic curves, 85
Encapsulating Security Payload (ESP), 151
encryption, 10
transport and tunnel mode of, 155–157
ESP. See Encapsulating Security Payload (ESP)
Euler's totient function, 66
F
factorization attack, 77
Federal Information Processing Standard (FIPS 186), 117–119
model of, 36
file-infecting virus, 173
firewall, 178
limitations of, 178
firewall configurations, 182–83
forwardable ticket, 135
G
group, 19
H
hash function, 93
hash-based MAC (HMAC), 106–109
design objectives of, 107
HMAC. See Hash-based MAC (HMAC)
honeypots, 171
I
IDEA. See International Data
Encryption Algorithm (IDEA)
IKE. See Internet Key Exchange (IKE)
Improved PES (IPES), 53
International Data Encryption Algorithm (IDEA), 53
Internet Key Exchange (IKE), 157
Internet Security Association and Key Management Protocol (ISAKMP), 159
header format of, 159
intruders, 167
intrusion detection, 168
intrusion techniques, 167
IP address spoofing, 180
IPES. See Improved PES (IPES)
ISAKMP. See Internet Security Association and Key Management Protocol (ISAKMP)
iterated hash functions, 96
K
Kerberos
Kerberos principal, 131
Kerberos realm, 131
key, 10
key clustering, 50
key management, 14
functions of, 14
rules for maintaining, 14
keyed transposition cipher, 25, 32
keyless transposition cipher, 25, 31
L
logic bomb, 175
M
MAC. See message authentication code (MAC)
malicious software, 173
man-in-the-middle attack, 83
MD5 (message digest, version 5), 96–99
meet-in-the-middle attack, 52
message authentication, 91
attacks on, 91
types of authentication, 91
message authentication code (MAC), 92–93
Miller-Rabin algorithm, 68
modular arithmetic, 16
monoalphabetic cipher, 25
different techniques of, 25
multiplicative cipher, 27
mutual authentication protocol, 121–124
N
National Institute of Standards and Technology (NIST), 45
native audit records, 169
NESSIE. See New European Schemes for Signatures, Integrity, and Encryption (NESSIE)
New European Schemes for Signatures, Integrity, and Encryption (NESSIE), 104
NIST. See National Institute of Standards and Technology (NIST)
non-Feistel cipher, 38
O
onetime pad, 33
one-way authentication protocol, 124–125
Output Feedback (OFB) mode, 63–64
P
packet-filtering router, 179–180
passive attack, 2
password protection approaches, 168
password selection strategies, 172
PES. See Proposed Encryption Standard (PES)
PGP. See pretty good privacy (PGP)
plaintext, 9
plaintext attack, 78
polyalphabetic ciphers, 25, 28
technique of, 28
polymorphic virus, 173
possible weak keys, 50
postdatable ticket, 135
pretty good privacy (PGP), 139–142
concept of trust and legitimacy, 142–143
general format of, 145
key rings and, 142
steps followed for transmission and reception of, 142
structure of key rings of, 143–145
prime number, 65
private key, 112
product cipher, 36
Proposed Encryption Standard (PES), 53
public announcement, 78
public directory, 78
public-key authority, 79
public-key certificates, 79–80
public-key cryptography, 80–81
distribution of secret keys using, 80–81
public-key encryption technique, 125
R
Rabin-Miller test. See Miller-Rabin algorithm
renewable ticket, 135
ring, 19
RSA digital signature scheme, 115–117
S
secret key, 113
Secure Electronic Transaction (SET), 162–164
Secure Hash Algorithm (SHA), 99–103
Secure Hash Standard (SHS), 99
Secure Socket Layer (SSL), 160–161
secure/multipurpose Internet mail extension (S/MIME), 146–149
semi-weak keys, 50
SHA. See Secure Hash Algorithm (SHA)
Shannon's theory of diffusion and confusion, 35
shift cipher, 26
SHS. See Secure Hash Standard (SHS)
source routing attack, 180
spyware, 175
SSL record protocol, 160
steganography, 15
stream cipher, 32
substitution cipher, 25
symmetric-key cipher, 24
symmetric-key encipherment, 10
symmetric-key encryption technique, 124–125
T
timing attack, 78
tiny fragment attack, 180
Transport Layer Security (TLS), 162
transposition cipher, 25
Trojan horse, 175
trusted system, 183
V
Vigenere cipher, 30
Vital Information Resources Under Seize (Virus), 173–174
W
weak keys, 50
Whirlpool, 104
Whirlpool cryptographic hash function, 104–106
X
certificate renewable and, 137–138
certificate revocation and, 137–138
authentication procedure of, 138–139
